耗散耦合腔阵列耦合量子化腔场驱动三能级体系中的单光子输运∗
石永强 孔维龙 吴仁存 张文轩 谭磊
(兰州大学理论物理研究所,兰州 730000)
耗散耦合腔阵列耦合量子化腔场驱动三能级体系中的单光子输运∗
石永强 孔维龙 吴仁存 张文轩 谭磊†
(兰州大学理论物理研究所,兰州 730000)
(2016年8月29日收到;2016年12月13日收到修改稿)
基于准玻色方法,解析求解了环境作用下一维耦合腔阵列耦合一个量子化腔场驱动的级联型三能级原子系统中单光子输运的反射率、透射率和相应等效势的表达式,并详细讨论了耗散情况下控制参数对单光子输运的影响.研究结果表明:在实验范围内选择合适的参数时,原子耗散和腔场耗散都能使反射率峰值降低,但原子耗散影响反射率较大,同等参数取值条件下反射率峰值减小更为显著;更为重要的是对于在环境作用下的体系,通过调节原子和腔场之间的失谐以及驱动量子化腔场的光子数仍可使单光子接近达到全反射.
环境作用,耦合腔阵列,准玻色方法,单光子输运
1 引 言
基于高品质微腔与超冷原子耦合的实验和理论进展[1−6],耦合腔阵列耦合超冷原子(或者人造原子)已成为一种实验模拟器,其具有可操控性和独特可寻址性等特点.在量子光学中,已被用作实验平台成功地模拟强关联多体量子效应[7].另一方面,在调控单光子输运的理论[8−10]和实验[11−13]研究中,人们发现耦合腔阵列耦合一个或多个原子(或者人造原子)可以用来实现光子输运的量子操控[14].控制单光子在耦合腔阵列体系中的输运特性是目前量子光学领域研究的热点问题之一,已经引起了理论和实验研究方面的广泛关注.
许多研究小组已经提出了多种控制单光子在耦合腔阵列中传输的方法.例如:在耦合腔阵列的一个腔中嵌入一个频率可调的一个或者两个二能级,这个频率可调的二能级原子可以是一个真正的原子或人造原子(如一个量子点或一个量子位),结果表明,可以通过调节原子的频率来改变单光子的透射或反射率,形成量子开关[14,15].同时耦合腔阵列中嵌入一个或者两个耦合的三能级系统也已被研究.Gong等[15]基于电磁诱导透明的机理研究了耦合腔阵列中耦合一个或者两个Λ型三能级原子的单光子输运,研究结果表明:两个三能级原子间可出现单光子准束缚态,理论上预言了全光的量子相干单光子存储器的实现机制.Zhou等[16]和Lu等[17]开展了由一维耦合腔阵列组成的多量子通道交叉处耦合一个∆型或者Λ型三能级原子构成单光子路由器的理论研究.在耦合∆型三能级原子的路由器中,原子可以从入射通道中提取单光子,再通过经典场驱动,光子就可以从一个频道转变到另一个频道,在耦合Λ型三能级原子的路由器中,利用一个经典场把原子从亚稳态驱动到较高的激发态,展示了原子的∆自发辐射光子可以使入射光子从一个通道转变到另一个通道.此外,一维耦合腔阵列嵌入一个被额外腔场耦合的级联型三能级原子体系中的单光子输运理论也已开展[18],通过调节额外腔场中的光子数和失谐,可以控制单光子输运的反射率和透射率.
众所周知,量子光学系统会不可避免地与环境发生相互作用[19−21],这种相互作用会使系统发生耗散、退相干和纠缠等现象[22−34].因此,在研究光子输运时耗散的影响是一个不可忽略的因素.基于准玻色方法[35],我们小组首先开展了环境作用下耗散耦合腔阵列耦合二能级单光子输运的理论研究[36].研究结果表明:系统与环境的耦合将导致入射光子的能量不守恒,导致光子的透射率和反射率发生改变.当原子与腔场共振时,在原子与腔共振的区域,耗散使得中间的最小值增大,使得光子不完全反射,并且加宽了频谱;当原子与腔场大失谐时,耗散使得透射谱的峰值减小,使得光子不完全透射.其次我们研究了环境作用下耦合腔阵列耦合一个能级跃迁由经典场驱动的三能级原子体系中的光子输运[37].研究结果表明:三能级系统可以通过调节经典驱动场来控制单光子的传输,并且三能级原子可以用来做更高级的量子开关.本文拟把经典场驱动推广到量子化场驱动的情况.基于此,本文利用准玻色方法开展了环境作用下耦合腔阵列耦合级联型三能级原子体系中的一个能级跃迁由额外量子化腔场驱动情况下单光子输运的理论研究.在此基础上,详细讨论了原子和腔场耗散、额外量子化腔场光子数、失谐对单光子输运的影响.
2 环境作用下的模型及其解析解
我们考虑如图1所示环境作用的一维耦合腔阵列系统.该系统由无穷多个单模微腔和一个双模微腔构成,为简便起见,把双模腔的位置标记为0.系统的哈密顿量可表示为(=1)
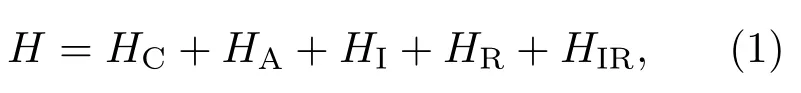
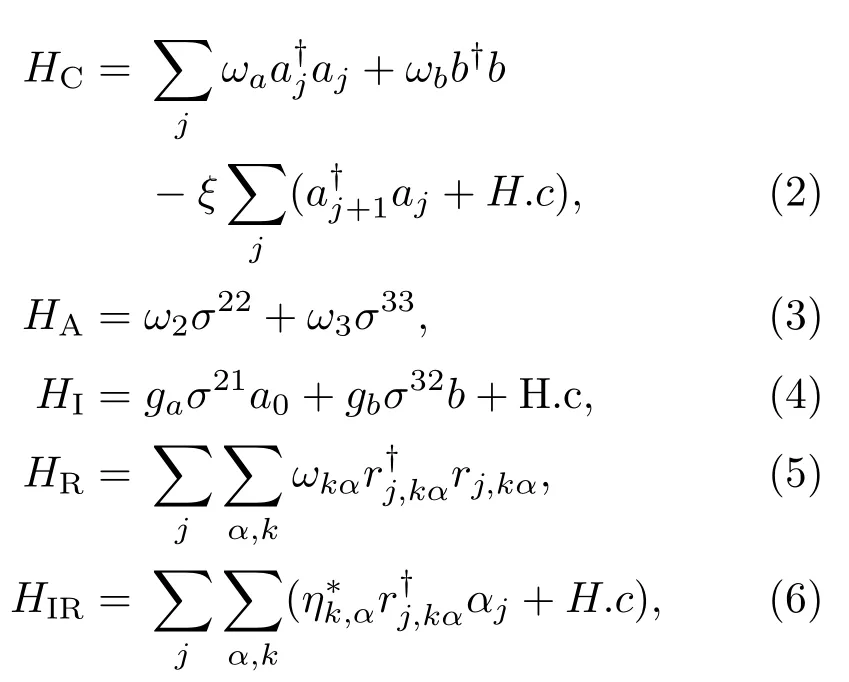
其中,HC,HA,HI分别为耦合腔阵列、三能级原子、双模腔与三能级原子相互作用的哈密顿量,HR,HIR分别为环境、腔场与环境相互作用的哈密顿量;α=a,c分别表示原子与腔场相对应的算符或物理量,ωkα表示环境的第kα个模式;分别表示在第j格点处环境第kα个模式的产生和湮灭算符,而ηkα为环境与腔场相应的相互作用耦合强度;和aj分别是第j个腔场模式的湮灭和产生算符.双模腔中的一个模式a0与邻近的其他单模腔发生最近邻耦合,相互作用强度为ξ=αωa,α的表达式在文献[36]中给出.b†(b)表示双模腔场另一个模式的产生(湮灭)算符.假设aj模式的腔场具有相同的共振频率ωa,b模腔场的共振频率为ωb.将一个级联型三能级原子放入双模腔中,三能级原子的能级分别由|1⟩,|2⟩,|3⟩表示,它们对应的本征频率分别为ω1,ω2,ω3,选取|1⟩为基态且能量取为0.原子的能级跃迁|1⟩↔|2⟩和|2⟩↔|3⟩之间的跃迁分别与腔场模式a0和b耦合,相应耦合强度分别为ga和gb.
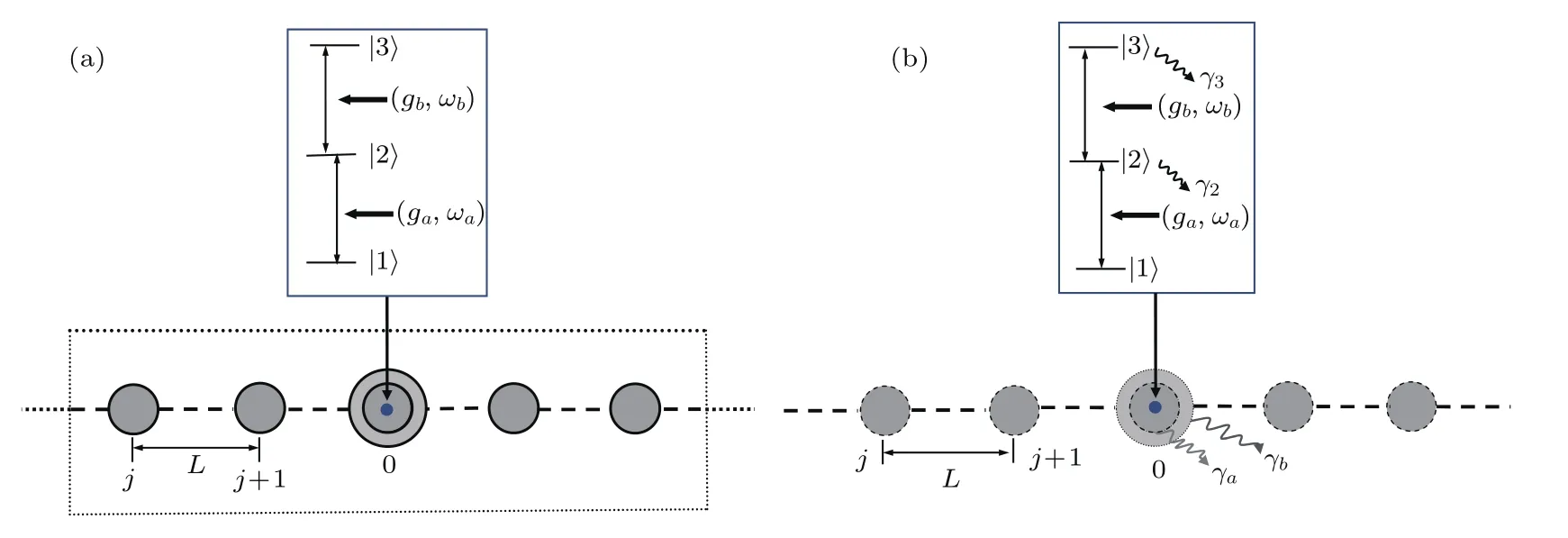
图1 环境作用下耦合腔阵列的模型示意图 (a)系统与环境发生相互作用,虚线表示环境;(b)准玻色子方法表示,耗散的耦合腔阵列可以看作一系列耦合起来的准玻色子,γa为a腔模的衰减率,γb为b腔模的衰减率,γ2为|2⟩能级的衰减率,γ3为|3⟩能级的衰减率Fig.1.Schematics of one dimensional arrays of coupled cavity under the environmental effects:(a)The coupling of the system to a bath;(b)effective treatment in a quasi-boson picture where the system can be regarded as a chain of quasi-bosons.The decay rates of a and b cavity modes is γaand γb,respectively.The decay rates of energy|2⟩and|3⟩are γ2and γ3.
利用准玻色方法剔除环境自由度后[35,36],系统哈密顿量可以表示为下面的形式:
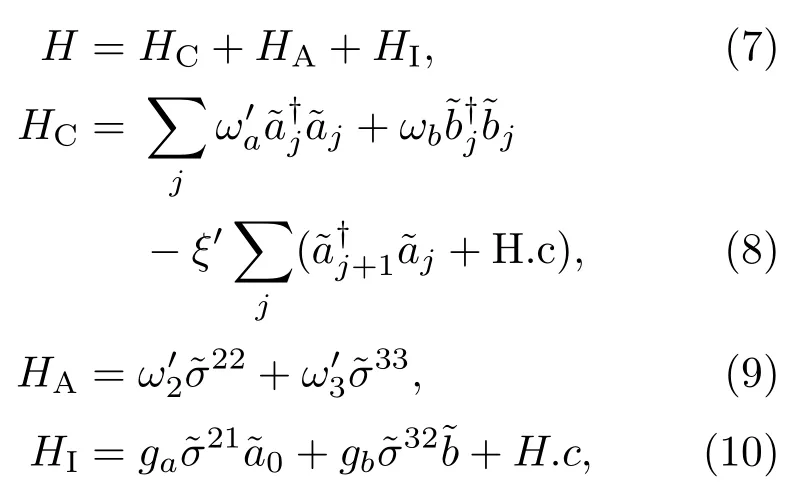
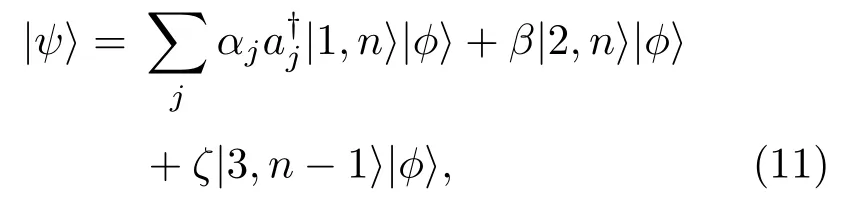
其中αj,β,ζ分别为相应态的概率幅. 在态|m,n⟩(m=1,2,3)中,m为原子所处的能级,n表示b模腔场中含有的光子数.|ϕ⟩表示真空态,意味着一维耦合腔阵列中不含有任何aj模式的光子.系统的本征方程可以写为
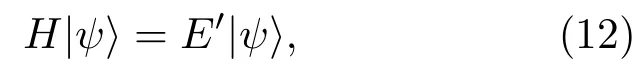
将(7)—(10)式和(11)式代入本征方程(12)中求解, 并在(11)式的左右两端分别用⟨ϕ|⟨1,n|aj,左乘可以得到以下三个方程:

将(13)式和(14)式代入(15)式化简消去β和ζ可以得到关于概率幅αj的离散方程
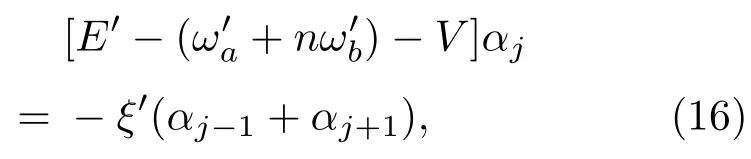
离散的散射方程(16)的形式解为

利用(17)式可求得当|j|>1时,2ξ′cosk.(16)式中的V可表示为
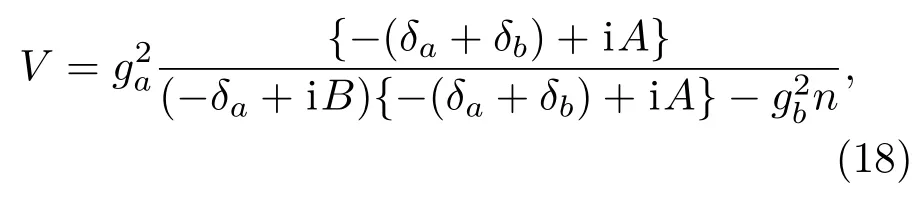
其中,δa=ω2− Ωk为能级|2⟩与腔场a模频率的失谐,Ωk=ωa−2ξcos(k).δb=ω32−ωb为能级|3⟩和能级|2⟩跃迁能量之差与腔场b模频率的失谐.A=2κcosk+γ3−γa−γb,B=2κcosk+γ2−γa.利用(15)—(17)式,则可以得到j=0处光子的反射系数为


光子的透射率和反射率可由下面的表达式分别给出

从表达式(19)中可以看出反射率和透射率与耗散参数γa,γb,γ2,γ3有关系. 当参数γa,γb,γ2和γ3都取零时,表达式(19)可给出理想情况下单光子输运的透射率和反射率.
3 耗散参数对单光子输运的影响
上节中,我们利用准玻色方法给出了系统的哈密顿量及其透射系数和反射系数的解析表达式.在本节中,首先讨论b腔的耗散对反射率的影响,然后在γ3和b腔的耗散为定值的前提条件下,讨论参数γa,γ2对反射率的影响,参数具体取值根据耦合腔阵列的相关实验[6],除去光子数n外,其余参数都是以ga为单位.
图2反映了耗散情况下反射率随腔场b与原子|1⟩↔|2⟩失谐δa的变化关系.可以看出反射率在δa=±1时取最大值,因此我们可以通过调节δa来控制光子输运.耗散参数的不同取值会改变单光子在耦合腔阵列体系中的反射率,随着腔场b耗散的增大,单光子反射率的峰值降低.当原子|1⟩↔|2⟩能级跃迁频率ω2增大时,反射率峰值逐渐增大.

图2 (网刊彩色)耗散情况下,单光子反射率随失谐的变化图像 (a)ω2=1,γb=(0,0.3,0.35)(红线,蓝线,绿线);(b)ω2=2,γb=(0,0.3,0.35)(红线,蓝线,绿线);其他参数取值分别为gb=1,n=1,δb=0,ωa=1,ξ =4,γa=0.3,γ2=0.3,γ3=0.3Fig.2.(color online)The single-photon transmission spectrum as a function of detuning δafor the dissipative case.The parameters are set as follows:(a)and(b)for the dissipative cavity case:γb=(0,0.3,0.35)(red,blue,green line).In(a)ω2=1,but for(b)ω2=2.The other parameters are gb=1,n=1,δb=0,ωa=1,ξ=4,γ2=0.3,γa=0.3,γ3=0.3.
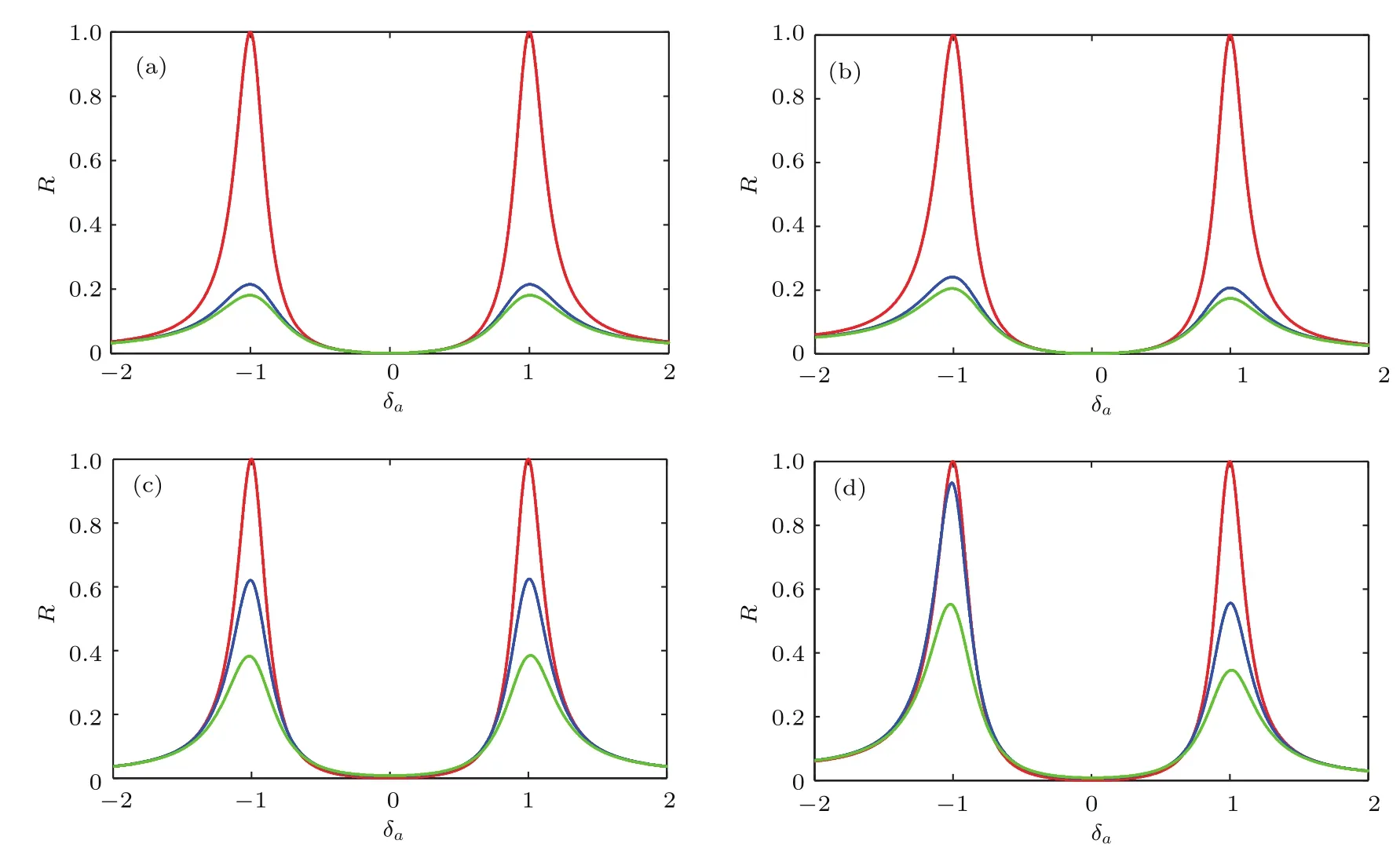
图3 (网刊彩色)耗散情况下,单光子反射率随失谐的变化图像 (a)ω2=1,γa=0,γ2=(0,0.3,0.35)(红线,蓝线,绿线);(b)ω2=2,γa=0;γ2=(0,0.3,0.35)(红线,蓝线,绿线);(c)ω2=1,γ2=0;γa=(0,0.3,0.35)(红线,蓝线,绿线);(d)ω2=2,γ2=0,γa=(0,0.3,0.35)(红线,蓝线,绿线);其他参数取值分别为gb=1,n=1,δb=0,ωa=1,ξ=2,γb=0.3,γ3=0.3Fig.3.(color online)The single-photon transmission spectrum as a function of detuning δafor the dissipative case.The parameters are set as follows:(a)and(b)for the dissipative atom case γa=0,γ2=(0,0.3,0.35)(red,blue,green line);(c)and(d)for the dissipative cavity case γ2=0,γa=(0,0.3,0.35)(red,blue,green line).In(a)and(c)ω2=1,but for(b)and(d)ω2=2.The other parameters are gb=1,n=1,δb=0,ωa=1,ξ =2,γb=0.3,γ3=0.3.
图3反映了耗散情况下反射率随腔场a与原子|1⟩↔|2⟩失谐δa的变化关系.可以看出反射率在δa=±1时取最大值,因此我们可以通过调节δa来控制光子输运.耗散参数的不同取值会改变单光子在耦合腔阵列体系中的反射率,随着原子和腔场耗散的增大,单光子反射率的峰值降低.数值计算结果表明,通过改变γ3也可调节反射率峰值的大小,其影响规律与γ2相同.通过对比图3(a)和图3(c)可以看出,当a腔场的频率与原子|1⟩↔|2⟩能级跃迁频率共振且原子的耗散与腔的耗散参数取相同值时,原子的耗散对反射率的影响更显著;图3(b)和图3(d)显示了原子与腔场非共振情况下反射率随失谐的变化关系,可以看出原子的耗散对反射率的影响比腔场耗散取相同值时的影响显著.耗散情况下腔场与原子共振与否还可影响光子反射率的对称性,从图3(a)和图3(b)的对比可看出,共振时,反射率关于δa=0呈现对称图像;非共振导致反射率出现不对称结果[38].当增加腔场的耗散时,这种不对称性表现得更为明显,图3(c)和图3(d)的比较显示了这个结果.从图3还可以看出,当体系和环境没有相互作用时,调节原子与腔场的频率并不能改变单光子反射率的对称性.控制参数对单光子输运反射率的调节,本质上可以理解为参数对等效势的调节[39].方程(18)式给出了环境作用下影响光子输运等效势的普遍表达式.在原子|2⟩↔|3⟩能级之间的跃迁频率与b腔中光子的频率共振情况下,并在耗散参数γ3为零和b腔无耗散[40]的前提条件下,当γa=0,γ20时,等效势为
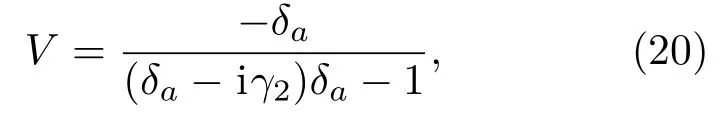
当γ2=0,γa0时,等效势为

从方程(20)和(21)可以看出改变参数δa,γa和γ2可以调节等效势的大小,继而可以改变单光子的反射率.在理想情况下,当δa=±1时,等效势V→∞,光子被势场全反射;在耗散情况下,当δa=±1时,等效势变为有限大小,并且等效势取值随着耗散参数的增大而减小,因此单光子被反射的概率随着耗散的增大会变小.
图4展示了耗散情况下失谐δb和光子数n的变化对单光子反射率的影响.可以看出改变失谐δb和调控光子数n可以改变单光子输运的反射率.在b腔场的频率与原子|2⟩↔|3⟩能级的跃迁频率共振情况下,随着光子数n的增大,单光子反射率先增大后减小,并在n=4处出现最大值.在非共振情况下,随着失谐δb的增大,单光子反射率的峰值逐渐向光子数增大的方向移动,并且峰值逐渐增大.当b腔中光子数取确定值时,随着失谐δb的增大,单光子反射率先增大后减小;当增加b腔中的光子时,单光子反射率峰值逐渐增大.从图4(a)中可以看出在δb=3,n=10时,单光子反射率趋于1.因此,耗散情况下可以通过同时调节失谐δb和光子数n使单光子达到接近全反射.通过图4(a)和图4(b)的比较同样可以看出原子|3⟩能级的耗散对单光子反射率的影响更显著.图4(c)给出了等效势随失谐δb和光子数n的变化关系,从图中可以看出单光子反射率的峰值与等效势峰值相对应,等效势越大单光子反射就会增强.在耗散情况下,单光子不会被全反射,原因就是系统与环境相互作用,这种相互作用会导致系统的耗散,致使单光子反射的等效势减小.
环境作用下,体系量子态存在的概率是随时间衰减的.随时间演化的态函数
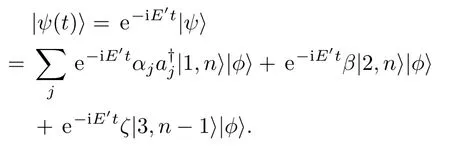
当|j|>1时,量子态|2,n⟩|ϕ⟩和|3,n−1⟩|ϕ⟩对应的概率分别为
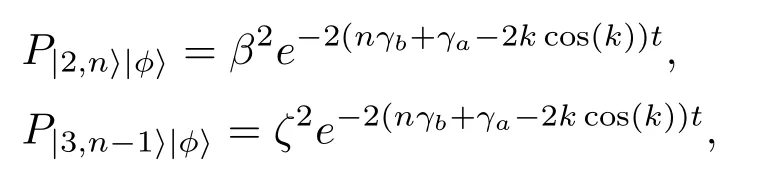
可见量子态的存在概率正比于P∝exp[−2(nγb+γa−2kcos(k))t].就本文研究的模型而言,时间尺度应控制在t≪1/2(nγb+γa−2kcos(k)).本文进行理论研究时控制变量的取值都是基于实验可调范围内的参数,因此研究结果对量子开关的具体实验实现具有一定的指导意义.在量子开关的具体实验中,腔场频率、腔与腔之间的耦合强度、量子微腔的品质因子及其体系的耗散皆可通过不同的实验方法调节.Transmission line resonator(TLR)的共振频率ωa可从2π×4—2π×4.8 GHz的范围内进行调节[41],其大小的改变可以通过增大或者减小TLR的电容来实现;实验上亦可通过在腔中存储氮气来调节腔的模式[42].相邻两腔的耦合强度定义为ξ=αωa,其大小亦可通过改变TLR的共振频率实现调节[43,44].一般来讲,体系耗散对量子开关的影响在腔的品质因子取值越大时变得越不显著,在PCC(photonic crystal cavity)中光子的寿命大于quantum dots(QD)退相位时间的范围内,腔的品质因子Q可以通过调节PCC的宽度来实现[45,46],而QD的共振频率则可以通过改变系统温度来进行调节[42].

图4 (网刊彩色)耗散情况下,反射率和等效势随失谐与光子数的变化图像 (a)γa=0.36,γ3=0;(b)γ3=0.36,γa=0;(c)γ3=0.36,γa=0;其他参数取值分别为gb=1,γb=0,γ3=0,ω2=3,ωa=1,ξ=2;除参数n外,其余参数取值都以ga为单位Fig.4.(color online)The reflection spectrum and effective potential versus the detuning and photon number:(a) γa=0.36,γ2=0;(b) γ2=0.36,γa=0;(c) γ2=0.36,γa=0.The other parameters are gb=1,γb=0,γ3=0,ω2=3,ωa=1,ξ=2.
4 结 论
本文研究了环境作用下耦合腔阵列耦合级联型三能级原子体系中的一个能级跃迁由额外量子化腔场驱动系统中的单光子的输运性质.详细探讨了原子的耗散和腔场的耗散对单光子输运反射率的影响.基于准玻色方法研究结果表明:环境的作用会使单光子反射率的峰值降低,原子的耗散对单光子反射率的影响更显著;而且耗散会破坏单光子反射率图像的对称性;更重要的是在耗散情况下,我们可以通过调节b腔的失谐和光子数使单光子接近达到全反射;系统与环境的耦合会导致入射光子的能量不守恒,这将影响光子的透射率和反射率,本文的研究可为实际体系中单光子的输运和量子开关的设计提供理论依据.
附录:等效哈密顿量的推导
我们课题组已在前期工作中[35,36]详细阐述了准玻色方法及其物理内涵,为了方便读者,本附录部分简要给出基于该方法的等效哈密顿量(5)—(7)式的推导过程.
考虑系统与环境的耦合时,可以将环境看作具有无穷多模式的库场.现在考虑一个单腔,假设库场的模式密度是均匀的,库场的连续模式密度由频率ωr表征,对于任意频率ωr对应的态密度ρ(ωr).假设由单个腔和库场耦合的系统中只有一个单光子激发,er和ea分别表示光子在腔或者库场中的概率幅,该系统的哈密顿量为
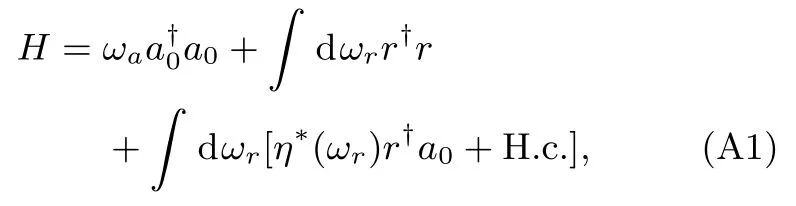
其中,r和r†分别为库场的频率为ωr的模式的湮灭和产生算符,它们满足的对易关系是η(ωr)是腔与库场之间的耦合强度.可以给出系统的形式波函数为

其中|0⟩表示真空态,系统满足本征方程

其中ω为系统能量的本征值.结合方程(A1),(A2)和(A3)并对(A3)式两端用⟨0|a0和⟨0|r取内积,可以得到下面的方程:



当腔场和环境的耦合较弱时,|η(ωr)|2/(ω−ωr)≪ω,可以认为发生了很小的频率移动.

对ω=ωr处的奇异性进行解析延拓,可以假设此模式下的库场与腔场的耦合最强,利用马尔可夫近似可得到

当腔与库场的耦合很弱的时候,可以将(A6)式写为

由于δωa相对于ωa为小量,因此可以将其略去或者将其吸收进ωa,因此腔和库场组成的系统的频率为一个复数

ω′a可以认为是考虑了与环境相互作用后的腔的本征频率,腔场和库场变成一个整体,本征频率加上了一个反映其寿命的虚部,耗散变成腔场的固有属性.此时可以引入一个准粒子来描述系统(准粒子对应的产生和湮灭算符分别用c†和c表示,近似满足玻色对易关系[c†,c]=1+iγ/ωa≈1).在准玻色算符表示下,方程(A3)中腔场和环境相互作用组成的系统的哈密顿量可以化为等效哈密顿量Heff,对应的本征方程为
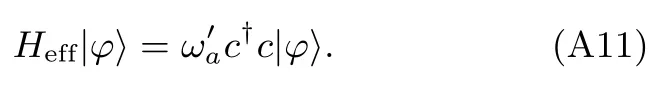
对于环境作用下的原子而言,由于Jaynes-Cummings模型中原子的升降算符是泡利算符(量子光学中常称为赝自旋算符),并不是玻色型算符,但我们将原子的激发态和基态描述为占据光子的态和没有占据光子的态,从而类比腔的处理模式引入准玻色子来描述环境作用下的原子,其本征频率记为ω′i=ωi−iγi以消除原子库场的自由度.
接下来,我们研究耦合腔阵列与环境相互作用的情况.通常情况下,真实环境的空间结构会导致不同位置有不同的态密度.环境是与每个腔耦合的,原子系统也是单独与环境发生相互作用.我们考虑每种环境的态密度是相同的,模型处理上相当于使用了一个均匀态密度的有效的大环境,每个腔和原子都与相同环境相互作用,并且假设每个腔具有相同的耗散率γa.c的对易关系与时间有关系,腔的最小的泄露不会对它们内部电磁场产生显著的变化.腔中光子的泄露会导致电磁场耦合成逐渐减小趋势,但我们仍可以用紧束缚近似方法,并且把这个系统仍看成准玻色链.
下面推导耦合腔阵列与环境耦合的情况.我们假设耦合腔阵列和一个大的态密度均匀的库场耦合,因此所有的腔都有相同的耗散率,研究表明周期性结构引起的耗散相比单个腔的耗散可以忽略不计,在有效的时间尺度内,较小的单个腔的耗散率不会对腔内电磁场的内部模式产生明显的影响,紧束缚模型对环境作用下的耦合腔阵列仍然有效,在准玻色框架下,耦合腔阵列可以看成是一个准玻色子链.
腔内电磁场相关的本征模ψj满足
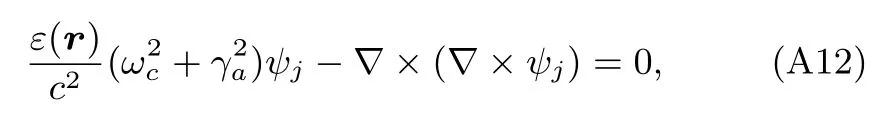
因此,相关叠加处的积分表达式为

因此,我们可以得到耗散耦合腔阵列的哈密顿量

利用上面的准玻色方法,剔除环境自由度后,系统哈密顿量可以表示为下面的形式:

最后,我们对准玻色子图像表示下系统的波函数进行一点说明.以耗散的腔场为例,由于(A11)式是关于准玻色子的对角化形式,其本征函数应同理想腔场形式相同,记为其中a是系统拥有一个准玻色子的概率幅.从该表达式可以看出,随着时间的演化,这个准玻色子逐渐从腔中“扩散”到整个系统.与此同时,指数因子将为提供一个衰减因子即与(A2)式中随时间衰减的ea对应的是在准玻色子图像表示下,本征函数是一种准模(quasinormal-mode)或阻尼基(damping basis).
[1]Raimond J M,Brune M,Haroche S 2001Rev.Mod.Phys.73 565
[2]Mabuchi H,Doherty A C 2002Science298 1372
[3]Wallra ffA,Schuster D I,Blais A,Frunzio L,Huang R S,Majer J,Kumar S,Girvin S M,Schoelkopf R J 2004Nature431 162
[4]Birnbaum K M,Boca A,Miller R,Boozer A D,Northup T E,Kimble H J 2005Nature436 87
[5]Xia F,Sekaric L,Vlasov Y 2007Nat.Photonics1 65
[6]Notomi M,Kuramochi E,Tanabe T 2008Nat.Photonics2 741
[7]Hartmann M J,Brandao F G S L,Plenio M B 2008Laser Photonics Rev.2 527
[8]Rosenblit M,Horak P,Helsby S,Folman R 2004Phys.Rev.A70 053808
[9]Bermel P,Rodriguez A,Johnson S G,Joannopoulos J D,Soljacic M 2006Phys.Rev.A74 043818
[10]Romero G,García-Ripoll J J,Solano E 2009Phys.Rev.Lett.102 173602
[11]Aoki T,Dayan B,Wilcut E,Bowen W P,Parkins A S,Kippenberg T J,Vahala K J,Kimble H J 2006Nature443 671
[12]Srinivasan K,Painter O 2007Nature450 862
[13]Rakher M T,Ma L,Slattery O,Tang X,Srinivasan K 2010Nat.Photonics4 786
[14]Zhou L,Gong Z R,Liu Y X,Sun C P,Nori F 2008Phys.Rev.Lett.101 100501
[15]Gong Z R,Lan H,Zhou L,Sun C P 2008Phys.Rev.A78 053806
[16]Zhou L,Yang L P,Li Y,Sun C P 2013Phys.Rev.Lett.111 103604
[17]Lu J,Zhou L,Kuang L M,Nori F 2014Phys.Rev.A89 013805
[18]Yan W B,Fan H 2014Phys.Rev.A90 053807
[19]Diehl S,Micheli A,Kantian A,Kraus B,Büchler P H,Zoller P 2008Nat.Phys.4 878
[20]Gerace D,Türeci H E,Imamolu A,Giovannetti V,Fazio R 2009Nat.Phys.5 281
[21]Karasik I R,Wiseman M H 2011Phys.Rev.Lett.106 020406
[22]Hur K L 2008Ann.Phys.323 2208
[23]Szymaska H M,Keeling J,Littlewood B P 2006Phys.Rev.Lett.96 230602
[24]Dalidovich D,Kennett P M 2009Phys.Rev.A79 053611
[25]Carusotto I,Gerace D,Tureci H E,DeLiberato S,Ciuti C,Imamolu A 2009Phys.Rev.Lett.103 033601
[26]Diehl S,Tomadin A,Micheli A,Fazio R,Zoller P 2010Phys.Rev.Lett.105 015702
[27]Schmidt S,Gerace D,Houck A A,Blatter G,Türeci H E 2010Phys.Rev.B82 100507
[28]Tomadin A,Giovannetti V,Fazio R,Gerace D,Carusotto I,Türeci H E,Imamolu A 2010Phys.Rev.A81 061801
[29]Hartmann J M 2010Phys.Rev.Lett.104 113601
[30]Morrison S,Parkins S A 2008Phys.Rev.Lett.100 040403
[31]Kiffner M,Hartmann J M 2010Phys.Rev.A81 021806
[32]Ferretti S,Andreani C L,Türeci H E,Gerace D 2010Phys.Rev.A82 013841
[33]Han J Y,Chan H Y,Yi W,Daley J A,Diehl S,Zoller P,Duan M L 2009Phys.Rev.Lett.103 070404
[34]Knap M,Arrigoni E,Linden W,Cole H J 2011Phys.Rev.A83 023821
[35]Liu K,Tan L,Lv C H,Liu W M 2011Phys.Rev.A83 063840
[36]Tan L,Hai L 2012J.Phys.B:At.Mol.Opt.Phys.45 035504
[37]Hai L,Tan L,Feng J S,Bao J,Lv C H,Wang B 2013Eur.Phys.J.D67 173
[38]Cheng M T,Ma X S,Ding M T,Luo Y Q,Zhao G X 2012Phys.Rev.A85 053840
[39]Flügge S 1999Practical Quantum Mechanics(Berlin:Springer-Verlag)pp64–68
[40]Sachiko K,Masashi B,Fumiaki S 2013J.Phys.B:At.Mol.Opt.Phys.46 224004
[41]Sandberg M,Wilson C M,Persson F,Bauch T,Johansson G,Shumeiko V,Duty T,Delsing P 2008Appl.Phys.Lett.92 203501
[42]Majumdar A,Rundquist A,Bajcsy M,Vuckovic J 2012Phys.Rev.B86 045315
[43]Liao J Q,Huang J F,Liu Y X,Kuang L M,Sun C P 2009Phys.Rev.A80 014301
[44]Houck A A,Schuster D I,Gambetta J M,Schreier J A,Johnson B R,Chow J M,Schoelkopf R J 2007Nature449 328
[45]Kuramochi E,Notomi M,Mitsugi S,Shinya A,Tanabe T,Watanabe T 2006Appl.Phys.Lett.88 041112
[46]Noda S,Fujita M,Asano T 2007Nat.Photonics1 449
PACS:42.50.Nn,42.65.–k,32.80.Qk DOI:10.7498/aps.66.054204
Single photon transport by a quantized cavity field driven cascade-type three-level atom in a dissipative coupled cavity array∗
Shi Yong-Qiang Kong Wei-Long Wu Ren-Cun Zhang Wen-Xuan Tan Lei†
(Institute of Theoretical Physics,Lanzhou University,Lanzhou 730000,China)
29 August 2016;revised manuscript
13 December 2016)
In this paper,a new kind of quasi-boson method is used to eliminate the coordinates of the environment and redescribe the dissipative system by using an effective Hamiltonian;the localized mode and the interaction between cavities can be renormalized.Based on the quasi-boson approach,the single photon transport in one-dimensional coupled cavity array,with a driven cascade-type three-level atom embedded in one of the cavity,is investigated under the influence of the environment.The single-photon transmission and the reflection amplitudes are obtained analytically.And the additional effective potential induced by the interaction between the atom and the cavity is also derived.The effects of the controlling parameters on the reflection and transmission amplitudes are discussed with considering the dissipation.It is shown that the decay rates of the atoms and the cavity both reduce the reflection spectrum.But the dissipation of the atom has a significant influence on the reflection amplitude compared with the cavity decay under the same conditions.Due to the irreversible loss of energy,the photon number is non-conservative.Furthermore,the single-photon can be almost reflected by the three-level atom in the dissipative case when one adjusts the detuning and photon number of the quantized cavity field.The investigation will be of benefit to the realization of photon transport in a real experiment,which is also helpful for manipulating the photons in quantum information and quantum simulation.
environment effect,coupled cavity array,quasi-boson approach,single-photon transport
PACS:42.50.Nn,42.65.–k,32.80.Qk
10.7498/aps.66.054204
∗国家自然科学基金(批准号:11274148)资助的课题.
†通信作者.E-mail:tanlei@lzu.edu.cn
book=101,ebook=107
*Project supported by the National Natural Science Foundation of China(Grant No.11274148).
†Corresponding author.E-mail:tanlei@lzu.edu.cn

