基于多重影响力矩阵的有向加权网络节点重要性评估方法∗
王雨 郭进利
(上海理工大学管理学院,上海 200093)
基于多重影响力矩阵的有向加权网络节点重要性评估方法∗
王雨 郭进利†
(上海理工大学管理学院,上海 200093)
(2016年10月15日收到;2016年11月23日收到修改稿)
本文基于有向加权网络模型,构建了三个影响力矩阵,并利用层次分析法对其赋权求和,形成多重影响力矩阵,从而提出了一种基于该矩阵的节点重要性评价方法.该方法通过新定义的交叉强度指标,来表征节点的局部重要性;利用全网节点对待评估节点的重要性影响总值,来表征节点在全网中的相对重要性.在分析影响节点对待评估节点的影响比例时,既考虑到节点间的距离因素,又引入了最短路径条数因素;既考虑了该影响节点对网络中其他节点的影响关系,又考虑了网络中其他节点对该待评估节点的影响关系,使得评价方法更加全面.将算法运用于ARPA网络,结果表明,该方法能有效地区分各节点之间的差异.最后,对实验结果进行连锁故障的仿真对比实验,进一步验证了方法的有效性.
有向加权网络,节点重要性,多重影响力矩阵,最短路径条数
1 引 言
复杂网络具有非同质的拓扑结构,这决定了网络中的每个节点不可能具有完全相同的重要程度[1].因此,采用定量方法挖掘出网络中的关键节点,并对其性质进行针对性的分析和利用具有十分重要的意义[2],它有助于提高整个网络的可靠性与抗毁性[3,4].目前,节点重要性评估的研究多集中在无向或无权网络上[5−12],然而,现实世界中的网络多数是有向加权网络,不仅要考虑节点之间相互作用的强弱[12],还要考虑其方向[5].将节点重要性评估的研究拓展到有向加权网络,对于推动复杂网络的发展具有更为重要的实用价值.
国内外学者从不同角度提出了多种有价值的评价方法.“中心性”常用来衡量节点的重要性,常见的指标有度、接近中心性、介数、累计提名等.例如Jeong等[13]利用度指标研究了蛋白质网络.然而,度相同的节点在网络中的重要度未必相同.另外,度指标仅利用了节点最局部的邻居信息,并没有考虑节点在网络中的位置,其应用非常有限.Freeman[14]于1977年在研究社会网络时提出介数指标.但该指标需要计算网络中任意节点对之间的最短路径,其算法的时间复杂度较高,对于大规模网络并不适用.近年来,有学者开始基于信息扩散的视角识别网络中的关键节点.例如Kitsak等[15]提出利用k-核(ks)分解法来挖掘中心节点.该方法认为ks指标越大的节点越重要.然而,在BA网络和树形网络中,所有的节点具有相同的ks值,同层的节点无法比较其重要性.另外,该方法也不能直接运用于有向网络、加权网络.Lü等[16]提出了LeaderRank算法,该算法没有参数,相比经典的PageRank算法[17]更加精准.但是,标准的LeaderRank算法中背景节点和所有节点的连接都一样,不切合实际且不能直接运用到加权网络.
目前有向加权网络节点重要度评估的研究还相对较少.Xu等[18]借鉴PageRank算法,提出一个有向加权网络节点重要性的评价指标——DWCN-NodeRank.但是,该算法不能同时获得较高的评估精度和较快的收敛速度.Liu等[5]充分利用网络的拓扑结构特征和邻居节点的重要性,提出了一种基于交互信息的节点重要性评价方法,该方法将节点所包含的信息量作为其重要性的衡量指标.节点所包含的信息越多,就越重要,这在一定程度上能区分节点间的差异.但该方法仅考虑了网络的有向性,而没有对加权网络进行讨论,王班等[19]对其进行改进,使其适用于有向加权网络.但是,文献[5,19]均只考虑了邻居节点之间的交互信息,而忽略了那些非直接相邻的节点之间也可能沿着某路径进行信息交互,不够全面.周漩等[20]结合节点的效率和度值,提出了节点重要度贡献矩阵的概念,以此表示节点之间的相互依赖关系,进而判断节点的重要度.但是,该方法将节点的重要度平均贡献给邻居节点,且认为这种重要性依赖关系仅仅存在于邻居节点之间,与现实不符.实际上,当网络具有较强的连通性,即所有节点之间的关系比较紧密时,非邻居节点之间的相互依赖关系就不能被忽略.Hu等[21]以及范文礼和刘志刚[22]分别提出了基于重要度贡献关联矩阵和网络传输效率矩阵的节点重要性评价方法.这两种方法不仅认为邻居节点之间存在相互作用,而且考虑到非邻居节点也可通过某种途径向待评估节点贡献自身的重要度,克服了重要度贡献只依赖邻居节点的不足.但是,传输效率矩阵在判断重要性贡献比例值时,仅考虑了节点间的最短路径长度这一因素,显然不够全面.事实上,两节点间的相互影响程度还与二者之间的最短路径条数相关.
基于以上考虑,本文通过新定义的交叉强度指标,来表征有向加权网络中节点的局部重要性.为研究节点在全网中的相对重要性,本文不仅同时考虑了最短路径长度和最短路径条数两个影响因素,还分别从影响节点和待评估节点两个角度构建了另外两个影响力矩阵,以此来表示全网节点之间的重要性影响关系,进而提出了基于多重影响力矩阵的综合评价算法.本文结构如下:在第二部分,引入交叉强度指标及其他相关指标.在第三部分,构建三种影响力矩阵,并运用层次分析法求得“多重影响力矩阵”,进而提出评价算法.在第四部分,将评价方法运用于几个具体的有向加权网络,并进行仿真实验分析,以此验证算法的有效性.在最后一部分,给出本文的总结.
2 理论基础
有向加权复杂网络模型G=(V,E,W).其中V={v1,v2,···,vn}为节点集合,E={e1,e2,···,em}为边集合,(vi,vj)∈E,表示从节点vi到vj的一条有向边.网络节点数目为n=|V|,边数为m=|E|.邻接矩阵记为An×n=(aij),当且仅当存在一条从节点vi指向vj的有向边时aij=1,否则aij=0.W表示有向边的权重矩阵,wij表示有向边(vi,vj)的权值.有向加权网络的权重矩阵一般不对称,即wijwji.
在有向加权网络中,每个节点的强度可以分为入强度和出强度[23].强度指标将入强度和出强度简单相加,无法有效区分两者之间的差异.针对这一问题,本文把有向加权网络中入强度和出强度的概念相结合,提出节点交叉强度的概念.
定义1交叉强度.为了综合考虑节点的入强度和出强度,本文将节点vi的交叉强度定义如下:

其中,λ是一常数,它满足表示节点vi的入强度,表示节点vi的出强度.当λ>0.5时,节点的入强度被认为对节点的重要性影响程度更大;当λ<0.5时,节点的出强度被认为对节点的重要性影响程度更大.常数λ的不同取值会得到不同的节点交叉强度值,从而导致节点重要性评价结果产生一定差异.
由于本文所有算法是在相似权[24]原则下进行的,即连边的权重越大表示两点间的距离越小,关系越亲密,因此认为节点的入强度更能反映节点的重要性.比如其他用户转发某用户的微博数,相比该用户转发其他用户的微博数更能反映该用户的重要性;其他作者引用某作者的文章数,相比该作者引用的文章数更能反映该作者的重要性,等等.交叉强度对节点强度进行了拓展,是衡量节点重要性的局部指标.常数λ的引入也使该指标同样可以度量那些出度非常大但入度为0或入度非常大但出度为0的节点重要性,更自然的用于有向加权网络.
定义2节点效率[20].节点vi的效率是指从该节点到网络中其他节点之间距离倒数之和的平均值表示为

其中,dij表示从节点vi到节点vj的距离;1/dij表示从节点vi到节点vj的效率,记作eij.节点效率值可表征从该节点到达网络中其他节点的平均难易程度.效率值越大,说明该节点越可能处于网络的中心位置,它在信息传输和总发挥的作用越大.
定义3网络平均效率[25].网络的平均效率是指网络中所有节点对之间距离倒数之和的平均值,它用来表示网络信息流通的平均难易程度:
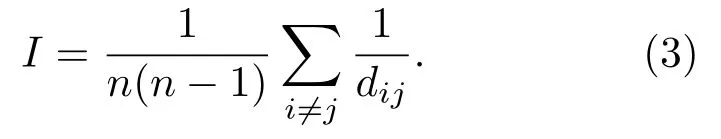
3 基于多重影响力矩阵的节点重要性评价方法
网络中的节点并不都是孤立存在的,而是受到其他节点的影响和制约.这种影响关系可以用节点重要性影响矩阵来描述.从信息传输路径的角度,网络中其他节点对某节点重要性的影响比例值会受到最短路径长度和最短路径条数两个因素的影响[14,26].需要注意的是,节点间的依赖关系不仅存在于邻居节点之间.当网络连通性较好,即节点之间具有较强的可达性时,非邻居节点仍可以通过其有效路径传递自身的重要性,从而影响所指向节点的重要性.这里的有效路径既可以是最短路径,也可以是非最短路径.本文假设节点会优先选择其最短路径进行信息传播,这样花费的成本最低[26].当然,节点通过非最短路径对其他节点施加的影响也需考虑在内.基于此,本文建立了三个重要性影响矩阵来表示节点间的这种重要性依赖关系.
3.1 基于效率的影响力矩阵
从空间自相关的角度,两个对象距离越远,对彼此的依赖程度越弱.利用空间自相关理论[27],可以认为:在其他条件相同时,网络中任一节点对待评估节点的影响比例与两节点之间的距离成反比,距离越大,重要性影响比例就越小.节点间的效率值eij是距离dij的倒数,该指标既表征了节点间相互作用的最直接、有效的形式,又体现了影响比重与距离的衰减关系,即当i=j或从vi到vj不存在路径时,eij=0;当vi直接指向vj时,其传输效率值最大,eij=1;当vi存在非直接到达vj的路径时,eij∈(0,1).因此,可构建如下效率矩阵E,它能从最短路径长度的角度反映节点间重要性的影响程度.

3.2 基于最短路径条数的影响力矩阵
节点间的重要性影响程度除了取决于两节点间的最短路径长度,还与连接两节点的路径数有关.不妨固定待评估节点vj,考察网络其他节点对vj的影响程度.假设从节点vi到vj的距离dij等于从节点vk到vj的距离dkj,但从vi到vj长度为dij的路径数远多于从vk到vj长度为dkj的路径数,那么在其他条件完全相同的情况下,vi要比vk更能影响vj的重要性.以朋友网络为例,假设A和B都能最少通过两层人物关系联系到C,但A既可以通过路径A→D→E→C,又可以通过路径A→F→G→C联系到C,而B仅能通过路径B→D→G→C联系到C.那么在其他条件完全相同的情况下,人物A对C的影响力就要大于B对C的影响力.同样地,固定影响节点vi,考察其对网络其他节点的影响程度,结论亦然.
在无向网络中,邻接矩阵具有重要性质[28]:邻接矩阵的k次幂里的元素值(Ak)ij(k∈Z+)等于对应节点对(vi,vj)之间长度为k的任意路径数.同样地,这条性质也可推广到有向网络.由于所以(A2)ij表示了从节点vi到节点vj所经历的长度为2的路径条数.对于任意正整数k(k>2),由于

所以,(Ak)ij表示了从节点vi到节点vj之间长度为k的路径总数.本文假设节点优先通过最短路径向网络中其他节点传播自身的重要性,因此可利用该条性质计算从节点vi到节点vj之间的最短路径数,即长度为dij的路径总数(Adij)ij.当i=j或从vi到vj不存在路径时,dij→∞,(Adij)ij=0.
需要特别强调的是,某节点vi(影响节点)对节点vj(待评估节点)的影响程度除了取决于两节点间的距离大小、最短路径条数,还取决于其他节点对vj的影响以及vi对其他节点的影响.比如,在其他条件不变时,如果网络中的其他节点均不对vj产生影响,那么vi对vj的影响程度就会相对变大,反之就会变小;另一方面,在其他条件不变时,如果vi仅对vj产生影响,而不存在指向其他节点的连边那么vi对vj的影响程度也会相对变大,反之就会变小.因此,可以基于最短路径条数对这两种情况进行分析,分别构建以源节点,即影响节点为中心的影响力矩阵SIP(source node-centred inlf uence power matrix)和以目标节点,即待评估节点为中心的影响力矩阵TIP(target node-centred influence power matrix):

对于矩阵SIP,元素为A1,2,···,n),其分子表示从节点vi到节点vj的最短路径数,即长度为dij的路径数,分母表示从节点vi到网络中所有节点长度为dij的路径数总和,二者的比值是从固定影响节点vi的角度,来分析其对vj的影响比例的;对于矩阵TIP,元素为,其分母表示网络中的所有节点到节点vj长度为dij的路径数总和,分子与分母的比值是从固定待评估节点vj的角度,来分析vi对其的影响比例的.由矩阵元素的分母表示还可以看出,这两个矩阵均考虑到了其他节点对在非自身最短路径上的信息传播对所研究节点对之间依赖程度的影响.
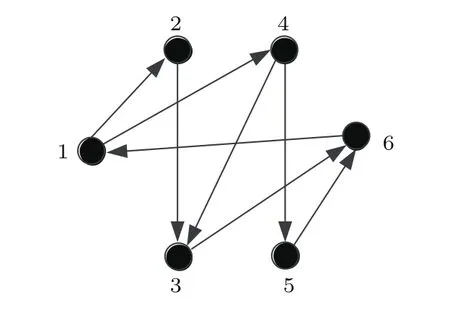
图1 一个简单的拓扑结构Fig.1.A simple topological structure.
图1是含有5个节点的简单拓扑结构,图2(a)和图2(b)分别是从某影响节点和待评估节点的角度提取的图1网络的部分拓扑结构.以此为例,利用上述3个矩阵,从不同角度比较各重要性影响比例值的大小.由于重要性影响比例是根据信息传输的路径来分析的,所以暂不考虑连边上的权重值.
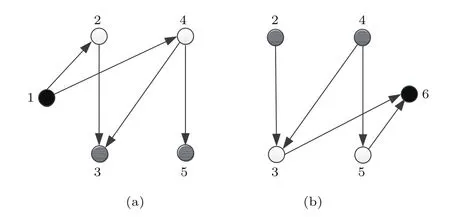
图2 分别从某影响节点和待评估节点的角度提取的图1网络的部分拓扑结构 (a)节点v1影响v3,v5的路径图;(b)节点v2,v4影响v6的路径图Fig.2.Part topology extracted from figure 1 from the perspective of acertain sourcenode and target node:(a)The path graph that v1influences v3and v5;(b)the path graph that v2and v4influence v6.
根据(4)—(6)式得:

效率矩阵主要用于两节点间距离不相等时的影响比例比较,而矩阵SIP和TIP分别是从影响节点和待评估节点的角度,用于两节点间距离相等时的影响比例的比较.一般来讲,当比较重要性影响比例大小时,首先要考虑的就是节点间的距离,然后再考虑距离相同时,SIP和TIP中元素的大小.
从节点间的效率角度,由于d13=2
从SIP的角度,比较同行元素.以v1对v3,v5的影响为例,图2(a)给出v1影响v3,v5的路径图.虽然e13=e15=0.5,但是由于v1到v3的最短路径数2大于v1到v5的最短路径数1,导致SIP13=0.67>SIP15=0.33.因此单从影响节点的角度,节点v1对v3的影响比例要大于v1对v5的影响比例.当然实际的影响比例还与v3,v5各自对应的TIP有关.
从TIP的角度,比较同列元素.以v2,v4对v6的影响为例,图2(b)给出v2,v4影响v6的路径图.虽然e26=e46=0.5,但是由于v4到v6的最短路径数2大于v2到v6的最短路径数1,导致TIP46=0.67>TIP26=0.33.因此单从待评估节点的角度,节点v4对v6的影响比例要大于v2对v6的影响比例.当然实际的影响比例还与v2,v4各自对应的SIP有关.
3.3 构建多重影响力矩阵
由以上分析可知,节点之间的影响程度同时受到节点间的距离、最短路径数以及影响节点对网络中所有节点的影响比例、网络中所有节点对待评估节点的影响比例的多重制约.因此,要想全面反映节点间的影响比例大小,就需要对矩阵E、矩阵SIP和TIP进行赋权加总,构建多重影响力矩阵.各矩阵权重的计算使用改进的层次分析法[29]得出,步骤如下:
第一步,采用(0,1,2)三标度法对每一个矩阵进行两两比较,建立比较矩阵;
第二步,利用极差法将比较矩阵转化为判断矩阵,并进行一致性检验,最后得到矩阵权重.具体的计算方法参见文献[29].表1列出了按照(7)式三标度法构造的比较矩阵B中的元素值.

表1 (0,1,2)三标度法构建各矩阵重要性的比较值Table 1.Importance comparison of matrix with(0,1,2)three-demarcation method.
表1中的比较矩阵

比较矩阵B的构建是基于以下考虑:效率矩阵E通过距离直接体现了节点间的亲疏关系,而且在比较节点间的影响比例值大小时,首先要考虑的是两节点之间的距离,然后再去考虑当距离相同时,最短路径数对比例值的影响.因此可认为效率矩阵E比其他两个矩阵更加重要;而矩阵SIP和TIP都是基于最短路径数来研究节点间的相互影响的,区别仅在于侧重点不同,SIP考虑到影响节点对网络中所有待评估节点的影响,TIP考虑到网络中所有影响节点对待评估节点的影响,这两种情况都需要考虑在内,无法比较其好坏,因此认为这两个矩阵具有同等的重要性.
经一致性检验,得到各矩阵的权重值分别为wE=0.82,wSIP=0.09,wTIP=0.09.对各矩阵加权求和,便得多重影响力矩阵M:

M中的元素mij表示考虑各因素后,节点vi对vj的综合影响比例值.由于节点效率值能体现该节点对于整个拓扑网络信息传输的贡献,因此,选取节点效率作为其对整个网络节点重要性影响的初始值.那么每个节点对网络中其余节点的依赖程度值便可用矩阵P表示:

矩阵P是多重影响力矩阵M的第i行中的数都乘以Ii得来的,其中pij=Iimij表示节点vi对vj的重要性综合影响值.在考虑全网节点对待评估节点重要性影响值的基础上,结合待评估节点自身的局部重要性(交叉强度值),可以定义节点vi的重要度Di:

归一化后,节点vi的重要度为

3.4 算法流程
本文算法充分考虑了节点的局部重要性和其受网络其他节点的依赖程度.已知网络的邻接矩阵A和权重矩阵W,其具体的算法步骤如下:
第一步,计算所有节点对之间的最短距离Dis=[dij]//有向网络的Floyd算法;
第三步,根据定义2,计算出每个节点的效率值Ii(i=1,···,n)和所有节点对之间的效率值eij(i,j=1,···,n),填入效率矩阵E;
第四步,根据各节点对之间的距离dij,计算所有涉及的矩阵Adij,并按式和将各比例值分别填入矩阵SIP和TIP中;
第五步,按照(8)式,确定多重影响矩阵M;将矩阵M的第i行中的数都乘以Ii,确定矩阵P;
第六步,根据(10)式和(11)式,计算每个节点的重要度
第七步,将所有节点按照重要性值从大到小进行排序.
考虑到有些节点仅存在出边,而不存在入边,比如微博网络中的“僵尸用户”,引文网络中的从未被引用的文章等,这时它们的重要度指标都为0.为了增强此类节点的可比性,本文对此类节点的处理如下:当两个节点的D′i值均为0时,比较二者的交叉强度值,值越大的节点,排序越靠前,节点越重要.
4 实证分析
4.1 算法有效性分析
首先以图3所示的具有对称结构的有向加权网络[19]为例,运用本文所提算法计算每个节点的交叉强度以及最终的重要性指标并与文献[19]中的交互信息评价方法进行对比分析.注意,文献[19]是对文献[5]的改进,使其评价方法能适用于有向加权网络(不妨令λ=0.8).
计算得到各节点的重要性指标值和排序结果,列于表2.
本文算法可以得出重要性的排序:v4和v7最重要,排在首位;v3和v8同等重要,仅次于v4,v7;v1和v9同等重要,次于v3,v8;v2和v10最不重要,排在末位.合理的解释为:从图3可以看出,节点v4和v7处于全局信息控制能力最大的位置,相当于两个“桥节点”,如果两个节点被删除,会直接导致网络不再连通,因此v4和v7的重要性最大;同样地,v3和v8的删除也会导致网络不连通,但相对于v4和v7,与v3和v8相关联的节点要少一些,因此重要性次之;v5和v6相互连接,但并没有起到“桥梁”的作用,因此重要性稍差;节点v1,v9和v2,v10在网络中的位置相同,都处于网络的边缘且都没有入边,但相对于v1,v9,节点v2,v10的出强度更小一些,因此排序就更为靠后.另外,从表2还可以看出,本文算法可以得出与文献[19]完全一致的前4个重要节点,再次说明了本文算法的有效性.
但是,本文算法与文献[19]在评价节点重要性上还是存在一定差异的,比如文献[19]认为节点v1,v9和v2,v10的重要性都要优先于v5和v6.为此表3给出了删除相应节点后网络的平均效率值的变化.由表3不难看出,删除节点v5后,网络的平均效率有所下降,这说明节点v5的删除在一定程度上减弱了网络的信息流通;而删除节点v1后,网络的平均效率反而上升,这说明节点v1的删除使得网络的通讯冗余度减少,反而提高了整个网络的通信能力.那么可以认为,节点v5和v6的重要性要大于v1,v9和v2,v10.因此,本文方法在评价节点重要性上相对更加准确.
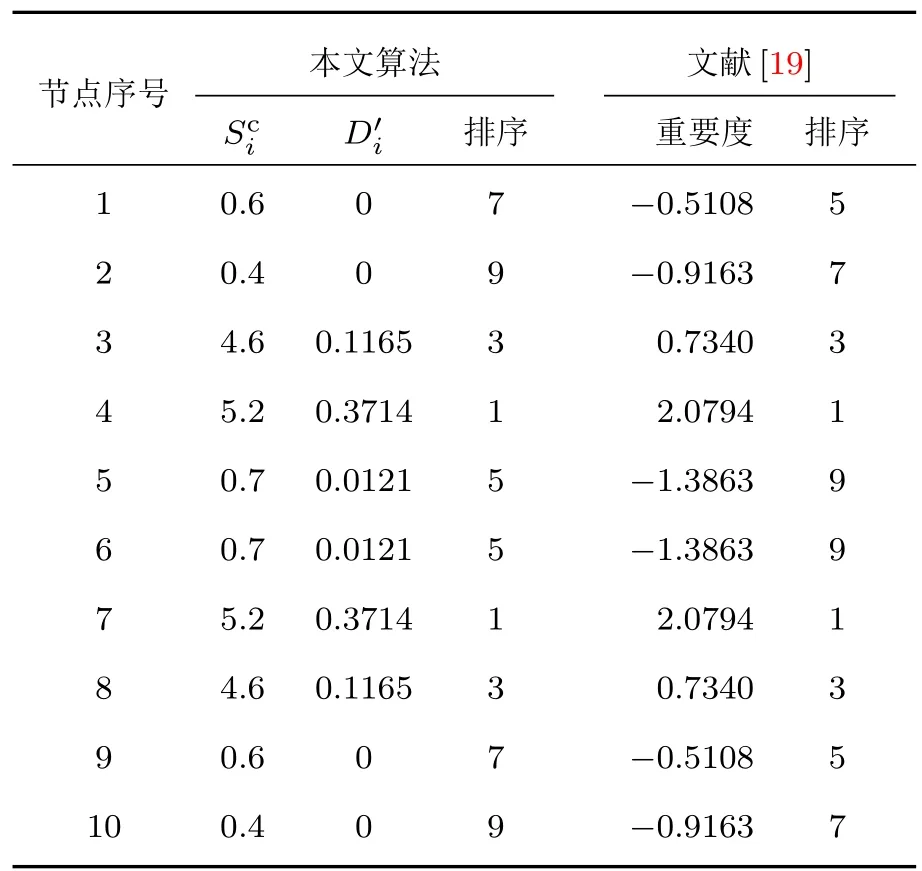
表2 图3所示网络的节点重要性排序结果Table 2.Importance ranking results of network nodes shown in Fig.3.

表3 删除相应节点前后图3网络的平均效率值Table 3.The average efficiency of network shown infigure 3 before and after removing node.
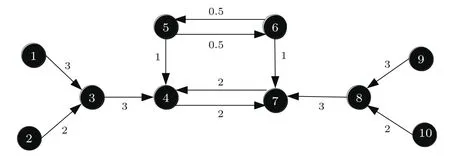
图3 具有对称结构的有向加权网络拓扑Fig.3.A directed weighted network topology with symmetric structure.
从对图3网络的实验可以看出,本文算法对简单的有向加权网络进行节点重要性评估可以取得良好的结果.为了进一步验证本文方法的有效性,本文利用了美国的ARPA(advanced research project agency)网络拓扑进行研究.ARPA拓扑属于无向无权网络,为此,本文先对其进行边赋权[30]得到无向加权网络,在此基础上再进行边定向[19]得到有向加权网络,如图4所示.其中边的定向原则是:首先计算加权网络中每个节点的强度,然后比较边(vi,vj)的两个端点vi与vj的强度大小.当Si 表4给出了本文所提算法以及文献[19,21,22]所述方法确定的节点重要性排序结果 (不妨令λ=0.8). 表4 加权定向后的ARPA网络节点重要性排序结果Table 4.Importance ranking results of nodes in directed weighted ARPA network. 图4 加权定向后的ARPA网络Fig.4.Directed weighted network obtained by the ARPA network. 首先从表4可以看出,本文的评价算法可以避免单纯地利用交叉强度指标的不足,考虑到全局因素的重要性指标能更好地区分节点之间的差异.比如,节点以此认为它们具有相同的重要性是太过片面的.考虑到节点在全网中的相对重要性pi值(p7=0.1817,p11=0.1984,p20=0.1194),可见v20在整个网络中的相对重要性明显小于v7和v11,因此D′i指标得到v20的重要性明显小于v7和v11. 另外,从表4的节点标注还可以看出,本文算法确定的前5个重要节点为v2,v14,v3,v19,v6,同时它们也属于文献[19,21,22]确定的前5个重要节点集的并集里,这符合网络的中心性评估,反映了本文算法的有效性.然而,文献[19]排在第5位的重要节点v9在本文算法和文献[22]中却排在末位,在文献[21]中也排在倒数第二位.从图4可以直观看出,节点v9所处的位置及连边上的权重值均不占优势,其重要性相对较小.另外,文献[19]认为节点v8,v10,v11具有相同的重要性,而本文算法能将v11与v8,v10的重要性区别开来.经计算,删除节点v8后,网络的平均效率仅下降了0.5%,而删除节点v11后,网络的平均效率下降了4%.可以得出v11的重要性要大于v8,这与本文的评价结果相一致.因此,本文评价方法相对文献[19]更能细致地区分节点之间的差异. 由于节点的移除会降低网络的连通性,造成的连通性越差,则对应的评价方法越好.因此,本文基于表4的评价结果,通过连续移除前5个重要节点,来对比本文与另外两种评价方法的准确性.网络的连通性可采用移除节点后的子图数目和最大子图规模两个指标来衡量,子图数目越多,或最大子图所包含的节点数目越少,则说明网络连通性越差,对应的评价方法就越准确.实验结果如图5所示. 由图5可以看出,在移除前5个重要节点后,文献[21]和文献[22]的评价方法均导致了6个子图,其中最大子图的节点数目均为10.而利用本文算法能够导致7个子图,其中最大子图的节点数目为7.此结果表明,无论是从子图数目,还是从最大子图规模的衡量上,本文算法的表现都要优于其他方法.因此,它在节点重要性评价上能取得良好的效果. 图5 (网刊彩色)移除前5个重要节点后ARPA网络连通性的变化Fig.5.(color online)The connectivity changes by removing the top 5 important nodes on the ARPA. 4.2 算法在连锁故障中的进一步验证 为了验证算法的可靠性,本文对ARPA网络进行连锁故障仿真来分析网络的鲁棒性.这里鲁棒性可采用两个指标来衡量.一个是故障后的子图数目S,另一个是连锁故障前后,网络最大连通子图的规模之比G,其表达式为 其中,nmax表示网络发生故障后最大连通子图的节点数目.连锁故障的过程如下:按照各方法得到的节点重要性先后顺序,依次移除网络中的重要节点.由于节点的移除影响着网络的鲁棒性[21],因此可以根据不同移除方式下的网络鲁棒性分析,来判断各评价方法的可靠性.G越小,S越大,说明网络鲁棒性越差,对应的评价方法就越可靠.本文及文献[21,22]对应的连锁故障仿真结果如图6所示. 图6 不同评价方法的连锁故障结果 (a)移除节点对指标G的影响;(b)移除节点对指标S的影响Fig.6.The results of cascading failures with different evaluation methods:(a)The effect of node removal on G;(b)the effect of node removal on S. 从G的变化趋势可以看出,在整体水平上,随着移除节点数目的增加,本文算法能造成G更大幅度的下降.虽然在删除第2个节点时,表现暂时落后,在删除前4个节点时,三种算法的表现持平,但是在后续删除节点的过程中,本文算法对应的G值都要小于文献[21,22].特别地,当连续移除前5个节点后,本文算法对应的最大连通子图的规模比文献[21,22]减少30%.此外,由S的变化趋势容易看出,本文算法对应的子图数目S上升较快,数值大小相对其他方法一直领先.由以上实验结果可以得出,本文所提出的节点重要性评价方法相对更加可靠. 本文通过分析节点的局部重要性以及网络中所有节点之间的依赖关系,提出了一种基于多重影响力矩阵的节点重要性评价方法.将该方法应用于几个典型的有向加权网络,得出以下结论. 相比其他方法,本文方法对ARPA网络节点重要性的区分更加细致.通过移除个别节点,本文方法得到的重要节点能造成网络平均效率更大程度的下降;通过连续移除前5个重要节点,计算网络连通性的变化,发现本文方法能造成更多的子图数目,以及更小的最大子图规模,这说明该方法具有一定的可靠性,其得到的重要节点能显著影响网络的连通性.进一步地,对网络进行连锁故障的仿真实验,结果表明该方法能造成G更大幅度的下降,对应的S值相对更大且上升更快,这再次验证了方法的适用性和可靠性. 部分入度为0的节点,其评价结果为0.对此本文是用交叉强度值对该类节点加以辅助区分的,如何针对该类节点设计出更准确的评价指标将是下一步的研究工作. [1]Barabási A L,Bonabeau E 2003Sci.Am.288 50 [2]Lü L Y,Chen D B,Ren X L,Zhang Q M,Zhang Y C,Zhou T 2016Phys.Rep.650 1 [3]Batool K,Niazi M A 2014PLoS One9 e90283 [4]Zhang Y L,Yang N D,Lall U 2016J.Syst.Sci.Syst.Eng.25 102 [5]Liu Y H,Jin J Z,Zhang Y,Xu C 2014J.Supercomput.67 723 [6]Han Z M,Wu Y,Tan X S,Duan D G,Yang W J 2015Acta Phys.Sin.64 058902(in Chinese)[韩忠明,吴杨,谭旭升,段大高,杨伟杰2015物理学报64 058902] [7]Li S M,Xu X H 2015Chinese J.Aeronaut.28 780 [8]Fan W L,Hu P,Liu Z G 2016IET Gener.Transm.Distrib.10 2027 [9]Liu R R,Jia C X,Zhang J L,Wang B H 2012J.Univ.Shanghai Sci.Technol.34 235(in Chinese)[刘润然, 贾春晓,章剑林,汪秉宏2012上海理工大学学报34 235] [10]Yu H,Liu Z,Li Y J 2013Acta Phys.Sin.62 020204(in Chinese)[于会,刘尊,李勇军 2013物理学报 62 020204] [11]Han Z M,Chen Y,Li M Q,Liu W,Yang W J 2016Acta Phys.Sin.65 168901(in Chinese)[韩忠明,陈炎,李梦琪,刘雯,杨伟杰2016物理学报65 168901] [12]Li J R,Yu L,Zhao J 2014J.UESTC.43 322(in Chinese)[李静茹,喻莉,赵佳 2014电子科技大学学报 43 322] [13]Jeong H,Mason S,Barabási A L 2001Nature411 41 [14]Freeman L 1977Sociometry40 35 [15]Kitsak M,Gallos L K,Havlin S,Liljeros F,Muchnik L,Stanley H E,Makse H A 2010Nat.Phys.6 888 [16]Lü L Y,Zhang Y C,Yeung C H,Zhou T 2011PLoS One6 e21202 [17]Brin S,Page L 1998Comput.Net.ISDN Syst.30 107 [18]Xu J,Li J X,Xu S 2012J.Zhejiang Univ.:Sci.C13 118 [19]Wang B,Ma R N,Wang G,Chen B 2015J.Comput.Appl.35 1820(in Chinese)[王班,马润年,王刚,陈波2015计算机应用35 1820] [20]Zhou X,Zhang F M,Li K W,Hui X B,Wu H S 2012Acta Phys.Sin.61 050201(in Chinese)[周漩,张凤鸣,李克武,惠晓滨,吴虎胜2012物理学报61 050201] [21]Hu P,Fan W L,Mei S W 2015Physica A:Stat.Mech.Appl.429 169 [22]Fan W L,Liu Z G 2014J.Southwest Jiaotong Univ.49 337(in Chinese)[范文礼,刘志刚2014西南交通大学学报49 337] [23]Kudelka M,Zehnalova S,Horak Z,Kromer P,Snasel V 2015Int.J.Appl.Math.Comput.Sci.25 281 [24]Thomas J B,Brier M R,Ortega M,Benzinger T L,Ances B M 2015Neurobiol.Aging36 401 [25]Latora V,Marchiori M 2007New J.Phys.9 188 [26]Shao F,Cheng B 2014Int.J.Comput.Commun.Cont.9 602 [27]Griffith D A,Chun Y 2015Netw.Spat.Econ.15 337 [28]Cai Q S,Liu Y,Niu J W,Sun L M 2015Acta Electron.Sinica.43 1705(in Chinese)[蔡青松,刘燕,牛建伟,孙利民2015电子学报43 1705] [29]Zhu Y,Meng Z Y,Kan S Y 1999J.Northern Jiaotong Univ.23 119(in Chinese)[朱茵,孟志勇,阚叔愚 1999北方交通大学学报23 119] [30]Sun S L,Lin J Y,Xie L H,Xiao W D 2007 22nd IEEE International Symposium on Intelligent ControlSingapore,October 1–3,2007 p7 PACS:02.10.Ox,89.75.Hc,89.75.Fb DOI:10.7498/aps.66.050201 Evaluation method of node importance in directed-weighted complex network based on multiple influence matrix∗ Wang Yu Guo Jin-Li† 15 October 2016;revised manuscript 23 November 2016) In complex networks,the node importance evaluation is of great significance for studying the robustness of network.The existing methods of evaluating the node importance mainly focus on undirected and unweighted networks,which fail to reflect the real scenarios comprehensively and objectively.In this paper,according to the directed and weighted complex network model,by analyzing the local importance of the nodes and the dependencies among all the nodes in the whole network,a new method of evaluating the node importance based on a multiple influence matrix is proposed.Firstly,the method defines the concept of cross strength to characterize the local importance of the nodes.The index not only distinguishes between the in-strength and out-strength of the nodes,but also helps to discriminate the differences in importance among each with an in-degree of 0.In addition,to characterize the global importance of the nodes to be evaluated,we use the total important influence value of all the nodes exerted on the nodes,which makes up the deficiencies of the other evaluation methods which just depend on adjacent nodes.Emphatically,in the analysis of the influence ratio of source node on node to be evaluated,we not only take into account the distance factor between nodes,but also introduce the number of the shortest path factors.In order to make the evaluation algorithm more accurate,according to the number of the shortest paths,we present two perspectives to analyze how other factors affect the influence ratio.One is to evaluate how this source node exerts important influence on the other nodes to be evaluated.The other is to analyze how the other source nodes perform important influence on this node to be evaluated.In view of the above factors,three influence matrices are constructed,including the efficiency matrix,and the other two influence matrices from the perspectives of fixing source nodes and target nodes,respectively.Then,we use analytic hierarchy process to weight the three matrices,thereby obtaining the multiple influence matrix,which makes the global importance evaluation more comprehensive.Finally,the method is applied to typical directed weighted networks.It is found that compared with other methods,our method can effectively distinguish between nodes.Furthermore,we carry out simulation experiments of cascading failure on each method.The simulation results further verify the effectiveness of the proposed method. directed-weighted complex network,node importance,multiple influence matrix,the number of shortest path PACS:02.10.Ox,89.75.Hc,89.75.Fb 10.7498/aps.66.050201 ∗国家自然科学基金(批准号:71571119)资助的课题. †通信作者.E-mail:phd5816@163.com *Project Supported by the National Natural Science Foundation of China(Grant No.71571119). †Corresponding author.E-mail:phd5816@163.com


5 结 论
(Business School,University of Shanghai for Science and Technology,Shanghai 200093,China)

