Fresnel波带片编码成像的高分辨重建∗
王心怡 范全平 魏来 杨祖华 张强强 陈勇 彭倩晏卓阳 肖沙里 曹磊峰
1)(中国工程物理研究院激光聚变研究中心,等离子体物理重点实验室,绵阳 621900)
2)(重庆大学,光电技术及系统教育部重点实验室,重庆 400030)
Fresnel波带片编码成像的高分辨重建∗
王心怡1)2)范全平1)魏来1)杨祖华1)张强强1)陈勇1)彭倩1)晏卓阳1)肖沙里2)曹磊峰1)†
1)(中国工程物理研究院激光聚变研究中心,等离子体物理重点实验室,绵阳 621900)
2)(重庆大学,光电技术及系统教育部重点实验室,重庆 400030)
(2016年8月24日收到;2016年11月30日收到修改稿)
本文提出了一种新的Fresnel波带片编码成像的重建方法.与传统的重建方法相比,这种新方法可以实现更高的空间分辨水平.具体而言,传统意义上来讲,Fresnel波带片编码成像的空间分辨水平取决于编码波带片的最外环宽度.本文提出的重建方法突破了这一限制,可以达到最外环宽度的1/m(m为正整数),从而超越了通常意义上的瑞利极限.
波带片编码成像,高分辨重建,Fresnel波带片,高阶Gabor波带片
1 引 言
波带片编码成像技术(ZPCI)是一种两步成像过程的技术:第一步是通过编码相机获得成像目标的编码图;第二步是根据获得的编码图重建出成像目标的空间分布信息.1961年由Mertz和Young提出[1],被广泛应用于天文学[2]、核医学[3]和激光惯性约束聚变研究等领域[4−6].其在惯性约束聚变研究(inertial confinement fusion,ICF)领域的应用和发展尤其吸引人们的注意,这是因为对于ICF研究中的低通量、高能辐射(α粒子、中子、质子、γ射线和高能X射线等)的探测,其他成像技术难以奏效.ZPCI技术有很多变种,在ICF研究领域内,经常使用的包括:环孔编码显微成像(RAM)技术、半影编码显微成像(PAM)技术和均匀冗余阵列编码成像(URA)技术等,其中ZPCI,RAM和PAM技术应用最多,这三种编码成像技术中,ZPCI技术应当是最好的[7],但RAM和PAM的编码孔更容易制作,因此后来的ICF研究中,反而是后者应用更多.美国LLNL实验室最早[8]报道了波带片编码技术在ICF研究中的应用,解决了激光聚变研究中高能量低通量辐射的成像[5,6,9]问题,后来也利用了RAM成像技术[10,11]和PAM成像技术等[12,13];法国[14]最早对PAM技术做了细致研究;英国[15]和澳大利亚[16]在ICF领域则主要使用的是PAM技术;国内于80年代末开始了编码成像技术在ICF研究领域的应用,1989年,胡家升等[17]开展了RAM技术的研究工作,着手研制环孔编码显微镜;2002年曹磊峰[18]研制了国内第一套α粒子Fresnel波带片编码相机,基于神光II实验装置,获得了国内第一幅激光聚变热核反应区域图像.
Mertz和Young最早提出波带片编码成像技术时,采用的是光学方法来完成编码图的重建.计算机技术快速发展后,退卷积的办法成为二维目标的标准重建方法[7].众所周知,空间分辨率是衡量成像器件性能的重要指标之一,Fresnel波带片编码成像的空间分辨率与波带片最外环宽度∆r有关,即只能分辨尺寸大于1.22∆r的物体[18].但在X波段,Fresnel波带片的最外环宽度∆r受加工工艺的限制,不可能非常小,这在一定程度上限制了Fresnel波带片编码成像的应用.本文针对上述问题,提出一种新型的波带片编码成像的重建算法,将其用于传统的Fresnel波带片编码图上,可获得打破瑞利判据限制的高分辨成像.下面,我们将从Fresnel波带片编码成像的数学表述和模拟实验两个方面对其进行研究.
2 Fresnel波带片编码成像的数学表述
如图1所示,波带片编码成像一般可分为两步:一是成像物(例如由两个点光源构成)照射到Fresnel波带片上,光线经波带片后投影、叠加到接收屏上形成编码图;二是用记录介质存储编码图像,并通过适当的算法对编码图进行解码,最后将成像物(或原始图像)重建出来.

图1 波带片编码成像的(a)流程图及(b)光路图Fig.1.(a)The flowchart and(b)the light-path diagram of zone plate coded imaging.
假设原始图像为f(x,y),Fresnel波带片的透过率函数为g(x,y),则根据编码成像相关理论,经波带片对原始图像编码后获得的编码图h(x,y)可表示为二者的卷积,即有h(x,y)=f(x,y)∗g(x,y).
在实际实验中,当采用记录介质测量获得原始图像的编码图后,可通过退卷积算法重建出成像物的原始图像.一般算法为F{h(x,y)}=F{f(x,y)}·F{g(x,y)}.通过适当的变换,有

其中,F表示傅里叶变换,F−1表示逆傅里叶变换,K为计算中用到的滤波常数.(1)式表明,未编码的原始图像可由经波带片编码的编码图的傅里叶变换与Fresnel波带片透过率函数的傅里叶变换相除的逆傅里叶变换得到.需要说明的是,(1)式的分母添加了一个滤波常数K,是噪声对信号的功率密度比.一般而言,K的值很难确定,需经过多次尝试才能找到合适的值.
Fresnel波带片成像的分辨能力受到波带片最外环宽度∆r的限制,即只能分辨尺寸大于1.22∆r的物体.所以,采用光学方法(即直接用单色平行光照射编码图,则在焦点处会产生一个原始图像的实像)对Fresnel波带片编码图进行重建的分辨率也受到最外环宽度的限制.通过计算发现,直接将Fresnel波带片的透过率函数g(x,y)代入(1)式,获得的重建图像分辨率与采用光学方法获得的结果是一致的.Fresnel波带片的透过率函数在极坐标下可以表示为

其中,∗表示两个函数的卷积,r1为Fresnel波带片的第一环半径,为第二环半径,m为波带片阶数.将上式做三角级数展开,可得
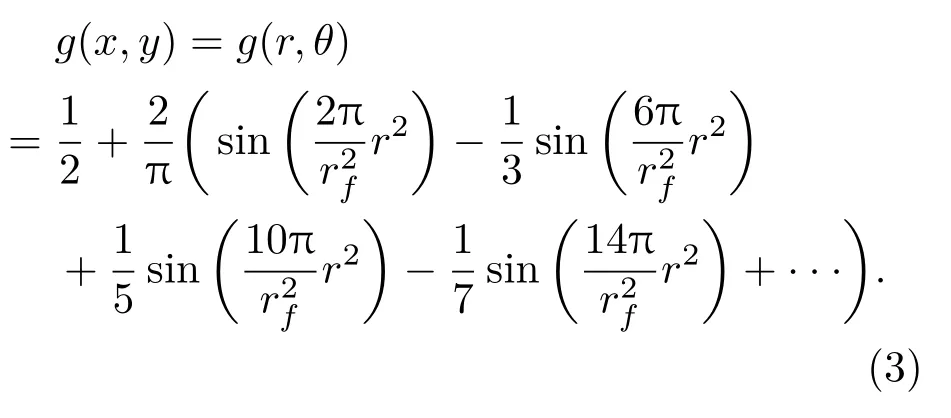
令(2)式中的m=2n+1,则(3)式可化简为
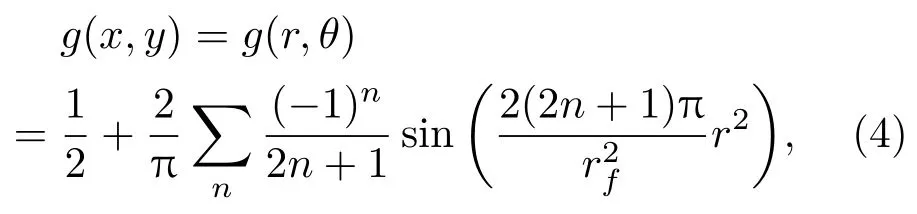
其中,n=0,1,2,3,···.假设与第一环半径为r1的Fresnel波带片对应的第m阶Gabor波带片透过率函数表示为
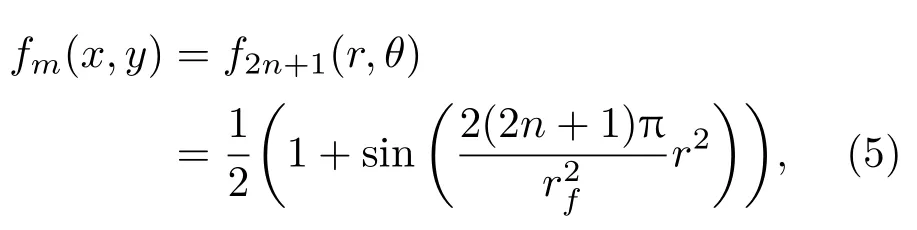
则将(5)式代入(4)式,可得
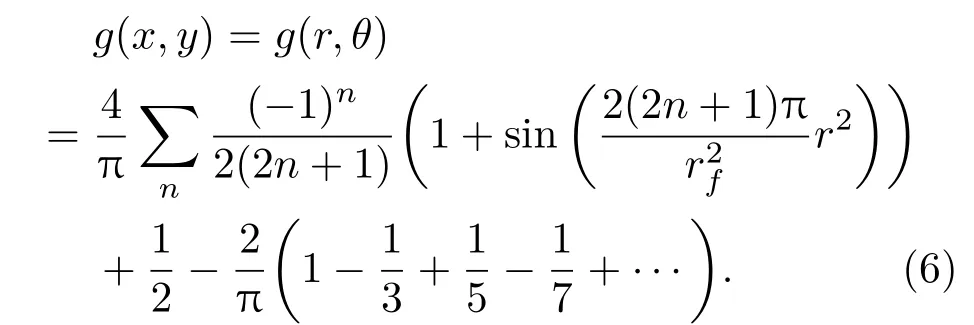
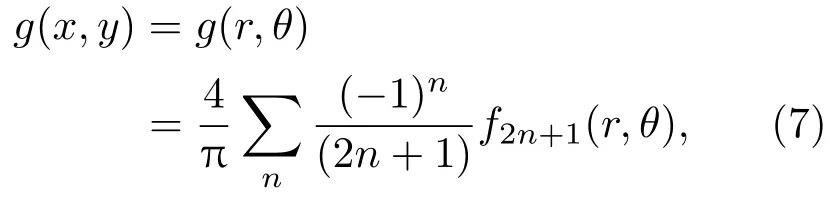
(7)式表明,Fresnel波带片的透过率函数可以表示为无穷多个不同阶次的Gabor波带片透过率函数的线性组合.因此,将Fresnel波带片作为编码孔获得的编码图h(x,y)又可表示为

下 面 我 们 将 第2n′+1阶Gabor波 带 片f2n′+1(r,θ)选为解码孔代替(1)式中的Fresnel波带片g(x,y),重建原始图像.即将(1)式变为

由于在n′n时,在一定的滤波条件下,有

因此(9)式只存在n′=n项.此时,可化简为

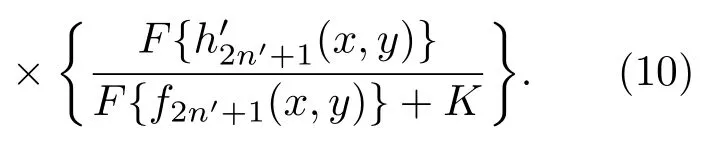
(10)式表明,采用第2n′+1阶Gabor波带片的透过率函数f2n′+1(r,θ)替代原来的Fresnel波带片的透过率函数g(x,y)对编码图进行解码,其效果等价于对编码图h(x,y)中所包含的成分进行重建.此时,重建图像的分辨率等于1.22∆r′.假设Fresnel波带片的第一环半径为r1,总环带数为N,则最外环宽度为则与Fresnel波带片对应的第m阶Gabor波带片的第一环半径总环带数N′=mN,则最外环宽度即第m阶Gabor波带片的最外环宽度∆r′是对应Fresnel波带片最外环宽度∆r的1/m倍.
推导证实采用这种方法获得的重建图像分辨率是直接采用(1)式方法的m倍.由于(10)式中存在因子1/(2n′+1),因此随着重建所用Gabor波带片阶次m=2n′+1的增高,所得重建图像的强度将随之减小,即所得重建图像的对比度也会随之变差.
3 模拟实验
我们用Fresnel波带片的第m阶Gabor波带片的透过率函数fm(x,y)代替原Fresnel波带片的透过率函数g(x,y),进行编码图的复原.假设原始图像为等腰三角形,其下底的长度l为10µm见图2(a);Fresnel波带片的环带数为N=50,第一环半径为r1=150µm,最外环宽度为∆r=10.6µm.如图2(b)所示.
由于l<1.22∆r,根据瑞利判据,经波带片直接成像无法获得清晰的图像.原始图像进行编码得到如图2(c)所示的编码图,再由退卷积获得如图2(d)所示的原始图像,可以看出,直接对Fresnel波带片g(x,y)进行退卷积,无法获得清晰的原始图,因为原始图像的尺寸太小,超过了瑞利判据的限制.
下面选取了某几个阶次的Gabor波带片代替原来的Fresnel波带片透过率函数g(x,y),进行退卷积运算对编码图进行复原,获得的复原图像结果如图3所示.
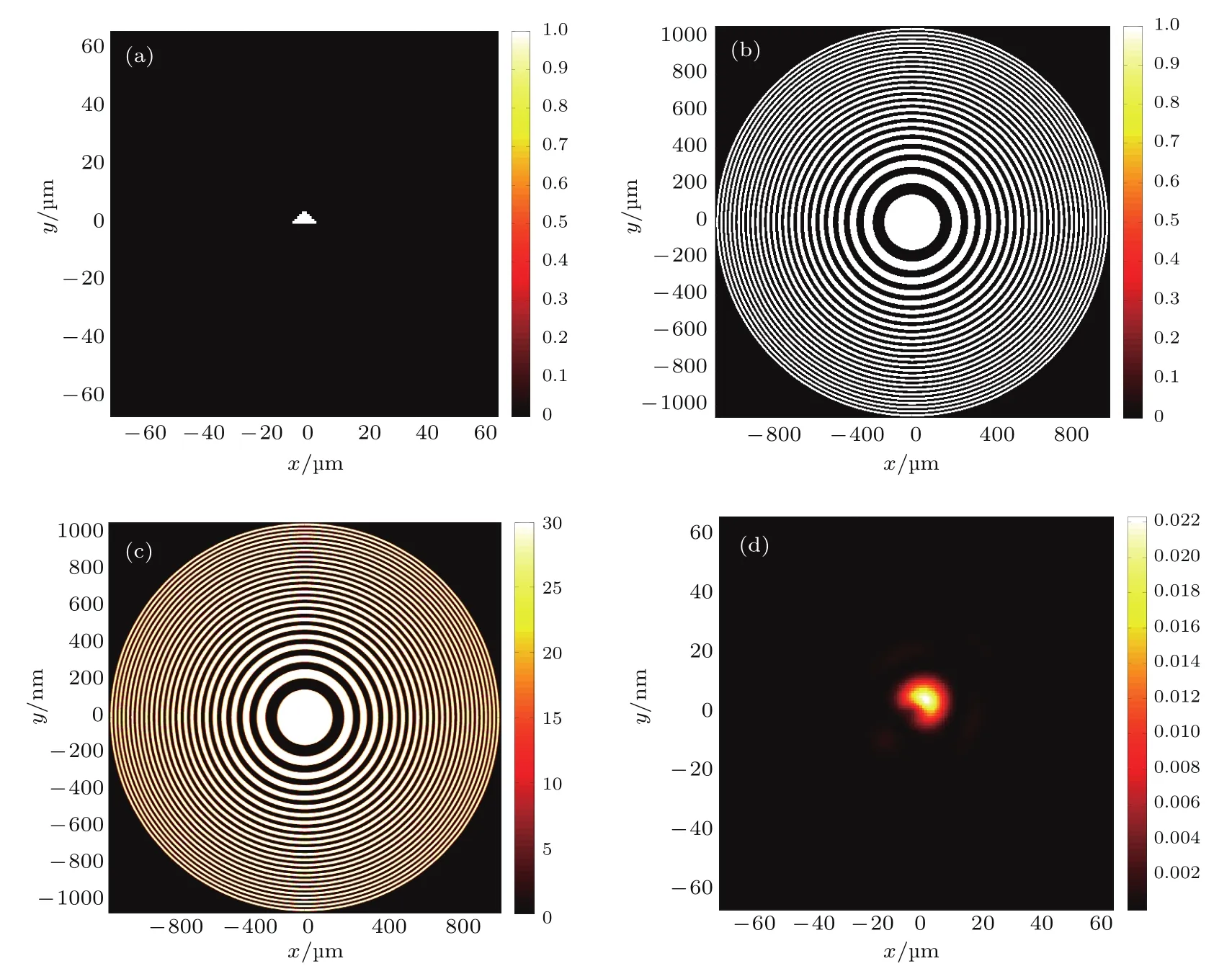
图2 (网刊彩色)编码成像步骤图 (a)原始图像;(b)Fresnel波带片;(c)编码图;(d)编码图退卷积后得到的复原图像Fig.2.(color online)Step diagram of zone plate code imaging:(a)The original image;(b)the Fresnel zone plate;(c)the coded image;(d)the result.
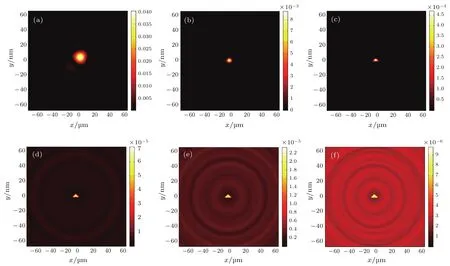
图3 (网刊彩色)用第n阶Gabor波带片退卷积得到的图像(a)—(f)分别为用第1,3,5,7,9,11阶Gabor波带片退卷积得到的图像Fig.3.(color online)The results through n-th order Gabor zone plate’s deconvolution:(a)–(f)The result through the first,third,fifth,seventh,ninth and eleventh order Gabor zone plate’s deconvolution,respectively.
由上述模拟结果可以看出,随着Gabor波带片的阶数的增加,获得的原始图像渐渐变清晰,当采用的Gabor波带片的阶次m取得足够高时,可以实现打破瑞利判据限制的高分辨成像,这表明,通过第m阶的Gabor波带片进行编码图的复原是提高复原后原始图像分辨率的有效手段.但随着Gabor波带片的阶次增高,复原得到的图像的背景噪声也随之增大.
4 结 论
我们提出一种新型的Fresnel波带片编码成像的重建方法:用Fresnel波带片的第m阶Gabor波带片进行编码图的重建.通过理论推导结合模拟分析,证实该方法能够实现打破瑞利判据限制的高分辨成像.一般地,使用第m阶Gabor波带片进行编码图的重建的分辨率是同等条件下采用Fresnel波带片进行重建的m倍.虽然随着分辨率的提高,复原得到的图像的对比度会随之变差,但被成像物仍然清晰可辨.总的来说该方法简单易行,为Fresnel波带片编码成像带来了新的生机.
[1]Mertz L,Young N O 1961Proceedings of International Conference on Optical Instruments and Tech-niques(London:Chapman&Hall)p305
[2]Chakrabarti S K,Palit S,Debnath D 2009Exp.Astron.24 109
[3]Barret H H 1972J.Opt.Soc.Am.13 382
[4]Ceglio N M,Attwood D T,George E V 1977J.Appl.Phys.48 1566
[5]Ceglio N M,Coleman L W 1977Phys.Rev.Lett.39 20
[6]Ceglio N M,Larsen J T 1980Phys.Rev.Lett.44 579
[7]Wen S H,Ding Y K 2012Laser Inertial Confinement Fusion Diagnostics(Beijing:National Defend Industry Press)pp270(in Chinese)[温树槐,丁永坤 2012激光惯性约束聚变诊断学(北京:国防工业出版社)第270页]
[8]Ceglio N M,Geroge E V 1975Am.Phys.Soc.20 1320
[9]Ceglio N M 1983Recent Advances in X-Ray Optics(Berlin:Springer Berlin Heidelberg)p97
[10]Ress D,Bell P M,Bradley D K 1993Rev.Sci.Instrum.64 1404
[11]Ress D,DaSilva L B,R A 1995Rev.Sci.Instrum.66 579
[12]Delage O 1995Rev.Sci.Instrum.66 1205
[13]Pollaine S M 2001Phys.Plasmas8 2357
[14]Brunol J,Sauneuf R,Gex J P 1979Opt.Commun.31 129
[15]Fews A P,Lamb M J,Savage M 1992Opt.Commun.94 259
[16]Nugent K A 1988Rev.Sci.Instrum.59 1658
[17]Hu J S,Cheng L H,Cao L F,Dong J J,Ding Y K 1989Acta Opt.Sin.9 263(in Chinese)[胡家升,程丽红,曹磊峰,董建军,丁永坤1989光学学报9 263]
[18]Cao L F 2002Ph.D.Dissertation(Mianyang:China Academy of Engineering Physics)(in Chinese)[曹磊峰2002博士学位论文 (绵阳:中国工程物理研究院激光聚变研究中心)]
PACS:42.30.Va,42.40.Kw DOI:10.7498/aps.66.054203
High-resolution reconstruction of Fresnel zone plate coded imaging∗
Wang Xin-Yi1)2)Fan Quan-Ping1)Wei Lai1)Yang Zu-Hua1)Zhang Qiang-Qiang1)Chen Yong1)Peng Qian1)Yan Zhuo-Yang1)Xiao Sha-Li2)Cao Lei-Feng1)†
1)(Research Center of Laser Fusion,China Academy of Engineering Physics,Mianyang 621900,China)
2)(Key Laboratory of Optoelectronic Technology and Systems of the Education Ministry of China,Chongqing University,Chongqing 400030,China)
24 August 2016;revised manuscript
30 November 2016)
Zone plate coded imaging is an experimental technique for particle and strong X-ray imaging,which is widely applied to astronomy,nuclear medicine,and laser inertial confinement fusion researches.From conventional perspective,spatial resolution of zone plate depends on the encoding zone plate width of outermost ring∆rwith a size greater than 1.22∆r.In X-ray region,however,the outermost ring width of Fresnel zone plate is limited by processing technology.Such a limitation makes it impossible to fabricate a sufficiently small zone plate,thus restricting the applications of Fresnel zone plate coded imaging.In this paper,we present a new reconstruction method of zone plate coded imaging by using a higher-order order Gabor zone plate.With the proposed method,higher spatial resolution can be achieved than with the regular methods,thus the spatial resolution is improved by 1/mtimes the width of outermost ring(wheremis a positive integer).Consequently such a breakthrough goes beyond the limits of Rayleigh criterion in general.
zone plate coding,high-resolution imaging,Fresnel zone plate,higher-order Gabor zone plate
PACS:42.30.Va,42.40.Kw
10.7498/aps.66.054203
∗国家重大科学仪器设备开发专项(批准号:2012YQ130125)和国家自然科学基金(批准号:11375160)资助的课题.
†通信作者.E-mail:leifeng.cao@cnep.cn
*Project supported by the National Key Scientific Instrument and Equipment Developmeng Project of China(Grant No.2012YQ130125)and the National Natural Science Foundation of China(Grant No.11375160).
†Corresponding author.E-mail:leifeng.cao@cnep.cn

