基于固溶体短程序结构的团簇式合金成分设计方法∗

姜贝贝 王清 董闯

(大连理工大学材料科学与工程学院,三束材料改性教育部重点实验室,大连 116024)

基于固溶体短程序结构的团簇式合金成分设计方法∗

姜贝贝 王清†董闯

(大连理工大学材料科学与工程学院,三束材料改性教育部重点实验室,大连 116024)

(2016年9月3日收到;2016年10月25日收到修改稿)

合金成分设计对于研发高性能复杂合金材料至关重要,是实现新材料研发由经验指导实验的传统模式向理论预测、实验验证的新模式转变的关键环节.总结了合金研发中常用设计方法的应用领域及存在的局限性,包括Hume-Rothery规则、电子理论、当量法、计算机模拟等.详细介绍了我们提出的基于固溶体局域短程序结构的团簇成分式设计方法.该方法建立在团簇加连接原子稳定固溶体结构模型基础上,其在不同复杂合金体系中的成功应用表明了该方法的普适性,为多元复杂合金成分设计提供了一种简单、精确的途径.

成分设计,多组元合金,团簇加连接原子结构模型,固溶体

1 引 言

高性能合金材料是高端制造业强国战略的物质基础,也是高新技术发展的先导.随着材料使役条件愈发苛刻,对材料性能的要求也越来越高.高性能合金材料通常是添加多个元素共同合金化来实现.为降低合金化元素添加的盲目性和复杂性,合金设计在高性能合金材料研发中至关重要.所谓合金设计是指在研制具有特定目标性能的合金时,在理论的指导下,确定母合金中加入合金元素的种类及其加入量,并能对性能加以预测.自从美国在2011年6月启动“材料基因组计划”后,欧盟多国、日本和印度等也迅速启动了类似的研究计划,争取在新一轮材料革命性发展中占有先机.我国也在积极应对“材料基因组计划”为国际材料发展带来的机遇和挑战,在“十三五”重点研发计划中启动了“材料基因工程关键技术与支撑平台重点专项”,以实现新材料研发由“经验指导实验”的传统模式向“理论预测、实验验证”的新模式转变,显著提高新材料的研发效率,最终达到新材料研发周期缩短一半、研发成本降低一半的目标.材料设计能为高性能新材料研发带来革命性飞跃,促成我国新材料领域的跨越式发展.

伴随着合金材料发展,材料设计也由最初的盲目试错法发展至现在具有针对性的设计.最初,人们常根据给定的成分选择合适的工艺处理方式,获得的性能与合金的组织相对应,最后再考虑合金的应用场合,“(成分+工艺)→组织→性能→应用”的模式可以称之为正序设计.然而,目前对于高性能合金的设计,研究者们常采用逆序模式思维,即根据合金的应用使役性能要求来设计合金.在此过程中,有两个环节至关重要,一个是根据使役性能要求确定合金的组织,另外一个是根据组织要求对合金进行设计,最终确定满足性能要求的合金成分及工艺.合金设计方法应运而生,从Hume-Rothery规则的经验设计到目前盛行的理论模拟,并将理论与实验融会贯通,以实现材料按需设计.目前,已发展了多种实用的合金成分设计方法,如Hume-Rothery规则[1]、元素当量法[2]、与电子理论相关的设计方法[3,4],以及计算机模拟计算方法等[5-7].众所周知,合金材料的性能与其微观组织结构密切相关,因此,基本单元元素组合-组织结构-基本性质之间的內禀关系一直是学者们欲揭示的最基本科学内涵.本课题组从局域原子结合的短程有序角度,提出了一种独特的合金设计方法--团簇加连接原子结构模型[8-10],旨在发展多组元合金化的成分设计原则,并在多个合金体系中获得应用.

本文将系统介绍几种常见的合金设计方法和基于团簇加连接原子模型的设计方法,以及各种方法的典型应用案例,以此为高性能新合金材料的研发提供理论支撑.

2 常见合金设计方法

2.1 Hume-Rothery规则

工程合金多以固溶体为基础,因此合金的固溶度理论一直是金属与合金理论研究的基础.早在20世纪30年代,Hume-Rothery形成固溶体的三个最基本的原则[1]：原子尺寸(溶质原子与溶剂原子的半径差Δr＜15%)、电负性(合金组元间电负性相差越小越易形成固溶体)和相对价电子(高价元素在低价元素中的固溶度大于对应较低价元素在高价元素的固溶度),主要用于Cu,Ag,Mg,V,Zr,Mo,Ta基等二元合金的固溶度的预测及成分设计.同时利用这三个因素也可确定金属间化合物的形成,如电子浓度化合物.但是利用原子尺寸因素规则预测可溶溶质的准确率仅为50%,为进一步提高Hume-Rothery设计原则的预测准确率,Darken和Gurry[11]将电负性因素定量化,并用溶剂元素的原子半径(r±15%)为横坐标,电负性(x±0.4)为纵坐标绘制了Darken-Gurry固溶度图,用椭圆将可溶区(椭圆内)与不可溶区(椭圆外)分开.此后,研究者们针对不同问题加入了更多的约束条件来提高预测固溶度的准确率[12-14].例如,Gschneidner[12]根据晶体结构类型将所有元素进行分类并总结规律,以预测固溶体类型及固溶度;随着热力学和金相理论的发展,Chelikowsky[13]引入了元素的电子化学势和电子密度参数,使得固溶体理论更为完善;在此基础上,Alonso和Simozar[14]又加入了原子尺寸因素,并将化学势函数和电子密度合并为混合焓,将固溶度的预测准确率提高到90%;Zhang和Liao[15]在键参数理论的基础上,将固溶极限定量为抛物线函数.尽管在多组元体系中,固溶度理论仍不完善,但Hume-Rothery规则依然是应用最为广泛的理论,其在特殊新材料,如亚稳态非晶合金和多主元高熵合金中的应用足以说明这一点[16,17].

2.2 与电子理论相关的方法

除原子尺寸因素外,电子因素是影响合金结构稳定的另一个重要因素.在电子理论基础上建立的合金设计与合金性能相关联的设计方法主要包括电子浓度方法、d电子轨道理论和经验电子理论方法.

2.2.1 电子浓度方法

电子浓度是表征合金结构稳定性的重要物理参量,早在Hume-Rothery规则中就指出了电子浓度对合金相结构的影响,电子浓度还可用来判断相结构和电子化合物的形成[18].电子浓度一般分为两类：有效价电子浓度和包含d电子在内的价电子浓度(CVE).过渡族元素的有效价电子浓度很难确定,故在多元复杂合金体系中更多地使用CVE参数,表示为其中CVEi和fi分别为元素i的价电子浓度和原子数分数.

Bagariatskii和Nosova[3]最先将电子浓度应用到钛合金的成分设计中,他们给出了Ti-TM(过渡金属)合金中的弹性模量E、相结构与电子浓度CVE之间的关系,随着CVE的增加,合金的BCC-β结构稳定性逐渐增强, 即发生α′′相→(α′′+ β)相→β相的变化过程(α′′为亚稳马氏体).合金的弹性模量E则先降低后升高,ω相(HCP结构的纳米相)的析出会使合金弹性模量升高;当合金CVE=4.15-4.24时,在保证β结构稳定性的同时,合金具有最低的弹性模量及优良的力学性能.根据这一理论,中国科学院金属研究所结合d电子理论研发了低弹性模量β-Ti合金(Ti-24Nb-4Zr-8Sn,质量分数,%),其CVE=4.15,弹性模量E=42 GPa[19].此外,在设计多主元高熵合金时,Guo等[20]指出合金的FCC,BCC固溶体结构的稳定性与价电子浓度CVE密切相关,当CVE≥8.0时为单一FCC结构,CVE＜6.87时为单一BCC结构,通过CVE因素可确定合金的结构并影响合金的力学性能.

目前,电子浓度因素已成为判断合金结构的一个重要物理参量,在Ni基高温合金和不锈钢等诸多常用合金体系中广泛应用[21].该方法简单易行,但对于多元合金体系,仅以一个简单的电子浓度参量来表征析出相和合金性能还存在一定的局限性,需要与其他因素结合使用.

2.2.2 d电子理论

d电子合金理论[4]是基于DV-Xαcluster模型的分子轨道计算发展而来的合金设计方法,又称新相分析法,由Morinaga等提出.通过DV-Xαcluster的分子轨道计算,可以有效研究各种晶体结构内局部区域的电子状态,该理论采用两个重要的物理参量：键级Bo和金属元素d电子轨道能级Md.参数Bo表示原子之间电子云的重叠,是原子间共价键强度的度量;参数Md为过渡族元素M的d电子轨道能,与合金元素M的电负性和金属键半径有关,可用作相结构稳定性的表征参量.对于多元复杂合金,采用平均值o和d来描述合金化效应,其中xi,Boi和Mdi分别为合金元素i的原子数分数、Bo和Md值.

该设计方法最先应用于Ni基高温合金中,成功控制了有害析出相σ的析出.确定高Cr抗热腐蚀合金相稳定性的临界条件[22],即和其中为消除γ/γ′共晶相析出的条件,为抑制有害脆性相的析出条件.此后,该方法也广泛应用于生物医用低弹性模量β-Ti合金[23]和Fe基不锈钢合金[24]中.例如,在Ti合金中运用d电子理论,可得相结构稳定图[23],可预测合金的相结构类型.可以看出,不同结构类型的Ti合金的变形方式位于不同区域内,Md值较低有利于β相的稳定,而Bo值较高有利于提高固溶强化效果;在β相合金区域内,弹性模量随着和值的增加而降低.一般低弹性模量医用Ti合金的因此,图可用于指导低弹性模量β-Ti合金的设计.日本丰田中央研究所成功设计了gum metal Ti-23Nb-0.7Ta-2Zr-1.2O(原子数分数,%),弹性变形超过2%[25];Kuroda等[26]设计的低模量合金Ti-29Nb-13Ta-4.6Zr(质量分数，%)的弹性模量仅为5-55 GPa.然而,d电子理论仍需大量实验数据作为支撑,且对于晶体结构类型的成因以及性能的影响仍需进一步探索.

2.2.3 固体与分子经验电子理论

固体与分子经验电子理论(EET)是余瑞璜教授[27]在能带理论、Pauling金属键理论和电子浓度理论的基础上提出的,以四个基本假设为基础,键距差(BLD)法为计算工具,求得晶格常数已知的晶体中键络上的电子分布和原子所处的状态.EET理论在金属材料和陶瓷材料等领域得到广泛应用[28-30],用于计算晶体的结合能、熔点、高压相变、转变压强和合金相图等内容.Liu和Lin[28]通过计算相晶胞上最强键上的共价电子对数nA及电子密度差Δρ,预测Q235带钢的抗拉强度和屈服强度,与实验结果符合得很好.Pang等[30]则计算了Mo2FeB2基陶瓷中硬质相的价电子结构,表明Mn的添加可以提高陶瓷硬质相的塑性和横向断裂强度.但是,EET理论还不够完善,在键距差小于0.005 nm时会产生多重解问题,计算值过度依赖实验值,并且在未知结构(例如非晶)的计算中误差较大.

2.3 当量法

当量是以合金体系中对某种特殊性能贡献突出的某元素作为参考,将其他元素的含量换算成与该元素相当的含量,计算累加得到所有合金元素折算后的特定元素含量值,即该种元素的当量.常用的合金当量有Mo当量、Al当量、Ni当量和Cr当量(舍夫勒组织图)等,这些当量被用于特定合金体系的设计.

Mo当量描述了不同合金化元素对β结构稳定性的贡献,是设计多组元亚稳β-Ti合金的一个重要方法.Bania[2]通过大量实验总结出Mo当量公式为me(Mo)=1.00m(Mo)+0.28m(Nb)+0.22m(Ta)+0.67m(V)+1.60m(Cr)+2.90m(Fe)-1.00(Al)(m为质量分数,%),并且提出β相结构稳定的下限值为me(Mo)=10%(质量分数).Mo当量法对设计生物医用低弹性模量β-Ti合金尤为重要,这类合金要求β结构稳定的同时具有低弹性模量,通常会在β稳定的下限处实现二者的结合.目前获得的低弹性模量β-Ti合金的Mo当量一般应控制在β稳定的下限[31].Al当量不仅是Ti合金设计强度的依据,也是热强钛合金热稳定性的判据,其表达式为me(Al)=1.0m(Al)+0.33m(Sn)+0.17m(Zr)+10.0m(O)(m为质量分数,%)[32].利用Al当量设计多元高温近α-Ti合金时,热稳定性好的近α-Ti合金的me(Al)=6.5%-9.0%(质量分数),而当me(Al)＞9.0%时,Ti3(Al/Sn)脆性相将从基体中析出,导致热稳定性下降.需要指出的是,Mo当量和Al当量公式中各合金元素的当量系数都是根据二元合金的实验结果换算得到的,即为Ti-M(M为合金元素Al,Mo,Zr,Sn,Fe等)二元合金β稳定临界下限成分与Ti-10Mo(即β稳定临界下限,质量分数,%)的比值.这种计算模式自身会引入实验误差,使多元合金设计中设计的准确性下降.

舍夫勒组织图[33]常用来表征不锈钢和焊缝金属的成分与相组织的定量关系(图1),其纵坐标为Ni当量(me(Ni)=m(Ni)+30m(C)+0.5m(Mn),m为质量分数,%),反映合金组织奥氏体化程度,横坐标为Cr当量(me(Cr)=m(Cr)+m(Mo)+1.5m(Si)+0.5m(Nb),m为质量分数,%),反映合金组织的铁素体化程度.根据Ni当量和Cr当量可将合金分为A(奥氏体),F(铁素体)和M(马氏体)区,从而预测并确定合金、异种钢焊接时焊缝的组织成分及性能.虽然舍夫勒组织图考虑了化学成分对组织的影响,但未考虑实际结晶条件及合金元素存在形态的影响.

图1 舍夫勒组织图[33]Fig.1.Schaeffler microstructure diagram[33].

此外,Cr当量还可单独用于描述不锈钢合金的耐腐蚀性能,即Tammannn/8规则[34]：Fe基固溶体的电极电位随Cr含量变化,当Cr和Fe物质的量比为n/8(n=1,2,···,8)时,Fe的电极电位会发生跳跃式升高,合金腐蚀现象显著减弱.此规则主要应用于不锈钢耐腐蚀性能的设计中.根据此规则,不锈钢中Cr的最低原子数分数为11.7%,但由于钢中有C的缘故,一部分C与Cr形成碳化物,为使固溶体中Cr的原子数分数不少于11.7%,实际不锈钢中含Cr量不低于13%.事实上,最初设计钢时还存在一个C当量,主要用于表征低合金钢的强度和可焊性,用CE或me(C)表示[35].国际焊接学会推荐使用me(C)=m(C)+m(Mn)/6+(m(Cr)+m(Mo)+m(V))/5+(m(Ni)+m(Cu))/15(m为质量分数,%)公式来评估含碳量偏高的中、高强度非调质低合金高强度钢的强度和焊接性能(me(C)的允许偏差为0.03%)[35].

2.4 计算机模拟计算

当传统方式严重制约了新材料的开发,难以满足现代复杂材料发展需求时,随着计算机技术的快速发展,基于不同理论方法建立起来的计算材料学形成了当今材料科学的一个崭新领域,可从电子层次、原子层次、微观及宏观层次分别进行模拟计算,其中典型的计算方法有第一性原理计算、分子动力学、蒙特卡罗法、有限元法、热力学计算等,同时也发展了模糊辨识法、遗传算法等合金设计方法.这些模拟计算方法将密度函数、原子势场、合金化元素种类及含量、相变转变温度等作为参量,通过计算机程序计算筛选得到优化的合金成分及性能,再对所设计的成分进行实验验证,建立模拟计算与合金性能之间的定性及定量关系,实现模拟计算指导实验,发展性能优良的新型复杂合金材料.下面简单介绍几种典型模拟计算方法的应用.

第一性原理是基于量子力学的密度泛函理论并以电子结构计算为基础的理论强度计算方法.采用5个基本物理常数(电子静止质量m0,电子电量e,普朗克常数h,光速c,玻尔兹曼常数kB),不依赖于任何经验参数,巧妙地将电子之间的交换关联势表示为密度泛函的形式,使材料的所有真实性质都可以由电子密度求出,从而预测微观体系的状态和性质.第一性原理被广泛应用于材料设计中,在计算和预测材料相变和相稳定性方面与实验结果具有很好的一致性[5,36,37],对新材料研发具有重要理论意义.Ghosh和Asta[5]采用基于密度泛函理论的第一性原理计算方法从能量和弹性稳定性角度成功预测了具有不同晶体结构的二元Al-TM合金的相稳定性及相转变趋势;Fu和Willaime[37]系统研究了BCC-Fe中He与空位、自间隙原子之间的相互作用,考察了形成的复合团簇的结构和稳定性,其理论结果能够很好地解释实验结果.但是,第一性原理计算模拟过程复杂,难以应用于多组元体系,目前只适用于简单体系.

遗传算法是模仿生物遗传进化过程开发的一种计算机模拟的概率搜索算法[38].Ikeda[39]提出将分子动力学模拟与遗传算法相结合用于多组分合金体系,可以大大降低单纯用分子动力学时所需的计算量,并用于Ni基高温合金的设计中.Xu等[6]基于热力学和物理冶金原理将遗传算法运用于超高强马氏体时效不锈钢的设计中,通过计算获得的合金经过实验验证,在固溶处理之后,合金的组织近乎全部为马氏体,经过时效处理,析出相均匀分布于马氏体基体上,从而使合金抗拉强度达到1270 MPa,且伸长率达到9%.此外,遗传算法多与其他理论(有限元分析法、分子动力学模拟、人工神经网络等)相结合,来解决材料设计中的优化问题.

误差反向传播(error backpropagation,BP)神经网络算法,将已有的实验数据作为信息数据输入计算机,利用计算机模拟反复学习,从而建立BP神经网络,根据成分与性能之间的定量关系建立预测模型,优化合金成分,适合研究复杂非线性系统和不确定过程.运用BP神经网络找出实验数据之间的潜在规律,能够避免传统方法(试错法或数学建模)的不足,有效地描述材料领域中工艺-组织-性能之间的复杂关系[7,40,41].Malinov和Sha[7]利用多层前馈神经网络分析和预测了钛合金材料的工艺参数和力学性能的关系,建立了合金成分、热处理参数和工作温度与钛合金材料的9个常用力学性能(抗拉强度、屈服强度、伸长率、断面收缩率、硬度、疲劳强度、冲击强度、弹性模量和断裂韧性)之间的关系,能对不同温度下钛合金材料的性能与各工艺参数之间的关系进行预测,实现工艺参数和热处理制度的优化.但是,神经网络算法建立的模型适用性较窄,对样本数据的依赖性较大.

以上方法通过大量实验数据统计得到适合某种或某几种合金体系的新型合金成分开发的参考依据,尽管有些方法运用相关物理理论(如d电子、第一性原理等)计算设计合金成分,但仍不能实现精确定量及从微观原子结构角度设计合金.

3 基于短程序结构的团簇成分式合金设计

对于以固溶体结构为基体的实用工程合金而言,其典型的局域结构特征就是溶质原子分布存在化学短程序.溶质元素尽管占据溶剂基体的晶格点阵位置,但从化学成分角度还不能确定溶质原子具体的占位,即存在化学长程无序;但由于溶质原子与基体存在不同程度的交互作用,因而存在偏离平均结构的化学短程有序分布.精密衍射实验证实,不同成分会产生不同的局域化学短程序,影响固溶体合金的性能[42-44].固溶体合金的局域短程序特征通常用Cowley短程序参数α表征[45],用来描述某一中心原子每个近邻壳层上的成分相对于平均成分的偏差.该参数只是用来描述固溶体结构的统计分布,不能给出局域结构的稳定性,至今无法量化描述固溶体结构,也不能对多元固溶体合金成分予以指导.因此,有必要定义类似的分子式能够代表固溶体结构的最小结构单元,以此给出典型成分单元,从而揭示固溶体合金的成分结构根源,这是合金成分设计的关键所在.

3.1 团簇加连接原子结构模型及团簇成分式

尽管溶质元素分布的化学短程序会在最近邻几个原子层上振荡存在,但由于电子对离子的屏蔽作用,其最强振荡偏差仍局限于第一个振荡周期内[46].因此,借助化学短程序概念,我们提出了团簇加连接原子结构模型,用于描述固溶体合金的理想短程序结构单元[8-10],旨在将固溶体合金的结构描述建立在溶质原子分布的短程局域有序基础之上.该模型将化学短程序结构理想地抽离为团簇和连接原子两部分,其中团簇是指围绕某个原子的最近邻壳层形成的配位多面体,而连接原子则位于团簇之间的间隙位置,即次近邻壳层.图2(a)所示为面心立方FCC点阵中的团簇加连接原子结构模型,其中[A-B12]团簇是指以A原子为心、被最近邻壳层上12个基体原子B所包围形成的立方八面体团簇,连接原子C位于团簇之间的间隙位置.不同种类溶质原子在团簇结构模型中的占位由溶质元素与基体元素之间的混合焓ΔH[47]来表征,ΔH为负表示溶质与基体之间存在强交互作用,此时溶质通常位于团簇心部,对应局域最强短程序作用;ΔH为正表示溶质与基体交互作用较弱,位于连接位置.事实上,组元间的混合焓也可描述短程序参数α[45].因此,该模型可给出一个简单团簇成分式,为[团簇](连接原子)x,其中连接原子的个数x由不同的团簇堆垛模式确定,即一个团簇与x个连接原子相匹配.我们用这种表达形式来描述固溶体中存在化学短程序的最小结构单元及对应的团簇成分式,只涉及最近邻的团簇和次近邻的连接原子.

根据此模型,我们研究了FCC和BCC两种固溶体结构中的团簇堆垛模式.在FCC固溶体中,以二元黄铜Cu-Zn合金为例.图2(b)为FCC Cu-Zn短程序结构模型[48],由于Cu-Zn间存在负混合焓,倾向于形成以溶质Zn为心、最近邻壳层为Cu原子的[Zn-Cu12]立方八面体团簇,而次近邻位置可被Zn或Cu原子占据,这与Cu-Zn单晶中通过中子衍射测得的短程序参数α相符合[44].由于次近邻壳层原子个数为6,故连接原子个数x≤6,最终构建出具有高稳定性的短程序结构单元[Zn-Cu12](Zn,Cu)1-6.例如最为常用的弹壳黄铜Cu-30Zn(添加Sn后又称海军铜)可以解析为[Zn-Cu12]Zn4=Cu-30Zn[9].这种源自化学短程序的简单成分式解释了工业合金的成分来源问题,也就是说,优质合金对应于高稳定性的局域结构单元和特定的团簇成分式,由此可明确给出合金化元素含量,从而形成了简洁而精确的工程合金设计新思想.

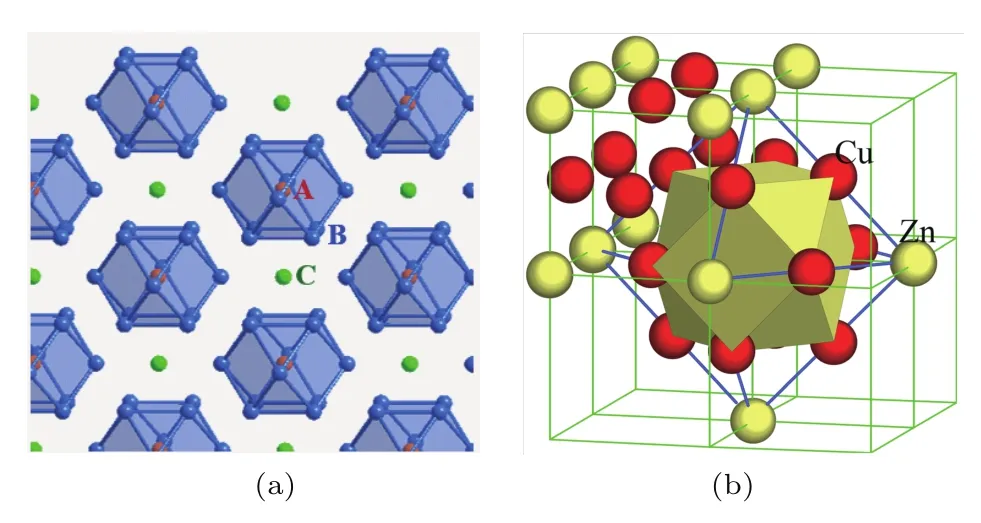
图2 (网刊彩色)(a)FCC固溶体合金中团簇加连接原子结构模型[A-B12]Cx;(b)Cu-Zn固溶体的局部短程序结构模型Fig.2.(color online)(a)The cluster-plus-glue-atom model[A-B12]Cxof FCC solid solution;(b)the local structural unit of short-range order of Cu-Zn.

对于BCC结构固溶体,采用的团簇为配位数CN14的菱形十二面体[C-(S1+S2)14],如图3(a)所示,C为团簇心部原子,S1和S2为团簇壳层原子,连接原子G位于次近邻位置.根据空间结构运算[10]得到,团簇孤立分布时得到的连接原子个数x=1-8,说明特征团簇外层的12个G原子位置最多允许同时有8个位置被连接原子占据.BCC固溶体合金的基本结构单元可以表达为团簇式[CS14]G1—8的形式.计算超团簇(多个团簇构成的有序结构)的空间密度：ρc=(Cc+1)/(d3×π×4/3),Cc表示以某一团簇为中心、与其近邻的其他团簇的个数,ρc则代表在距离中心团簇位置半径为d的球形范围内团簇的个数密度,平均密度ρa=1/[(1+14+x)×a3/2], 约化密度ρc/ρa代表团簇的密堆程度.当连接原子x=1时,团簇在空间中分布最密堆,此时CN14团簇按照类似面心立方结构(图3(b))排列,连接原子处于团簇堆垛的八面体间隙位置[10],此时团簇和连接原子能够实现化学成分的最大分离,体现了各原子间相互作用达到稳定后的近程序结果,对应固溶体合金的一种特殊稳定结构状态.

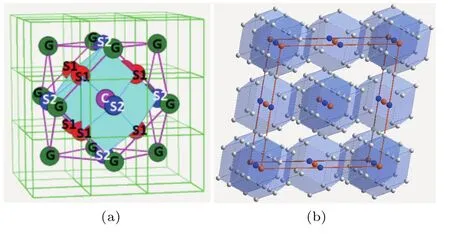
图3 (网刊彩色) (a)BCC固溶体局域短程序结构模型[C-(S1+S2)14]G1-8;(b)连接原子x=1时对应的CN14团簇堆垛模式[10]Fig.3. (color online) (a)The local structural unit of short-range order of BCC solid solution[C-(S1+S2)14]G1-8;(b)the cluster packing configuration of CN14 clusters in a pattern of BCC-like structure with a glue atom number ofx=1[10].

基于固溶体短程序结构的团簇成分式设计方法为实施合金成分优化提供了一种全新思路,并成功指导了多种合金体系的合金成分设计,包括Cu合金、特种不锈钢、Ti合金、Zr合金、高熵合金、亚稳合金等,下面举例介绍团簇成分式设计方法在各合金体系中的应用.

3.2 团簇成分式设计方法的应用

3.2.1 FCC固溶体合金

3.2.1.1 白铜合金

白铜合金为Cu-Ni基FCC固溶体合金,其中Ni是主要合金化元素,其质量分数为10%-30%,同时也会含有微量的Fe和Mn合金化元素,其质量分数为0.75%-1.3%.微量Fe,Mn的添加不但能提高合金抗海水腐蚀能力,同时也会提高其强度,利于合金的加工;然而过量添加会因为第二相Ni3(Fe,Mn)析出而降低基体的结构稳定性,从而导致Cu合金在拉拔过程中开裂.因此,如何控制微量元素的含量至关重要.以Cu-Ni-Fe三元[49]为例说明如何利用团簇结构模型解决Fe元素的微量添加问题.根据组元之间的相图和混合焓[47](ΔHCu-Ni=4 kJ/mol,ΔHCu-Fe=13 kJ/mol,ΔHFe-Ni=-2 kJ/mol)可知,Fe元素不溶于基体Cu中,但与主合金化元素Ni互溶且可形成中间相,Ni-Fe之间的ΔH为负,使得Ni-Fe原子趋于近邻,在FCC结构中形成以Fe为心、周围被12个Ni原子包围的[Fe-Ni12]团簇,如图4(a)所示,将这些孤立团簇均匀分散在Cu基体中,就会形成[Fe-Ni12]Cux稳定固溶体合金.Fe在Cu中的微量固溶可通过第三元素Ni来实现,并且当Fe/Ni的原子数之比为1/12时,微量Fe在富Cu的白铜合金中达到最大极限固溶度,如图4(b)所示,实验结果也表明Fe/Ni原子数比超过此比例时会有Ni3Fe相析出.此外,根据团簇成分式[Fe-Ni12]Cux设计的三个最大固溶度的白铜合金[Ni1/13Fe12/13]10Cu90,[Ni1/13Fe12/13]20Cu80和[Ni1/13Fe12/13]30Cu70(原子数分数,%)在模拟海水环境的溶液中具有最佳的耐腐蚀性能[49].因此,基于团簇结构模型的合金设计方法可以确定微量合金化元素添加的含量及固溶度极限.

由Cu-Ni-Fe三元可拓展至含有不溶于基体Cu的元素M的Cu-Ni-M体系中,其中M为Ce,V,Mo,Ru,Ta,W等,即M与Cu的ΔH为正[47],M与Ni的ΔH为负,这样可以形成[M-Ni12]Cux成分式,第三组元M的极限固溶度随Ni含量的变化而变化.对无扩散阻挡层Cu-Ni-Mo合金的研究表明,[Mo-Ni12]团簇成分比例是Mo元素微量添加的最佳方式,该比例能够保证Cu-Ni-Mo合金薄膜的热稳定性,且不与基体Si发生反应.其中,[Mo1/13-Ni12/13]0.3Cu99.7(原子分数,%)合金薄膜样品[50]在400°C退火1 h后仍保持单一FCC结构,未见Cu-Si反应物生成,合金薄膜同时具有最低的电导率,为2.6µΩ/cm.此外,蒙乃尔合金是一种含Cu,Fe,Mn的富Ni合金,与白铜合金属于同一合金体系,但位于相图的不同端,根据团簇结构模型,该合金仍满足团簇式[Fe-Ni12]Cux(x=5)[51].因此,Fe和Cu必须完全分离才能保证固溶体结构的稳定性,团簇式[Fe-Ni12]Cux为FCC结构的一种稳定形式.

图4 (网刊彩色) (a) FCC Cu-Ni-Fe合金的团簇结构模型[Fe-Ni12]Cux;(b)600◦C下Cu-Ni-Fe相图中Ni/Fe原子数比为12的成分线[49]Fig.4.(color online) (a) Cluster-plus-glue-atom model[Fe-Ni12]Cuxfor FCC Cu-Ni-Fe solid solution alloys;(b)the composition line where atom number ratio of Ni and Fe is 12 in the Cu-Ni-Fe ternary phase diagram at 600◦C[49].

3.2.1.2 马氏体时效不锈钢

超高强度马氏体时效不锈钢由于具有良好的强韧性匹配、可焊性、热加工性和较好的耐蚀性而被广泛应用.该类不锈钢以三元Fe-Ni-Cr为基础体系,高温下为单一FCC-γ奥氏体,水淬时要求奥氏体基体完全转变成马氏体组织,并且在低温时效过程中析出Ni3M(M为Nb,Ti,Mo,Al,V)化合物进一步强化基体.根据混合焓大小,Ni与基体Fe具有较强的交互作用,故在FCC奥氏体中形成[Ni-Fe12]团簇,Cr作为连接原子,则团簇成分式可表达为[Ni-Fe12]Crx.研究表明当x=3时恰对应奥氏体稳定的下限[51],可完全转变为马氏体,此时对应的结构模型为[Ni-Fe12]团簇按照类FCC模式堆垛,其间的四面体和八面体间隙由Cr原子填充,如图5所示.为确保时效过程中Ni3M析出后基体仍为马氏体,需要添加多余量的Ni,则多元合金化的团簇成分式为[Ni-Fe12](Cr2(Ni,M)1).在此成分式基础上,为体现微量元素M的添加含量,可将基础成分式自洽放大,即[Ni-Fe12](Cr2(Ni,M)1)=[Ni16-Fe192](Cr32(Ni16-x-y-z-m-nMoxTiyNbzAlmVn)).研究表明该系列合金固溶态和时效态的显微硬度HV都与合金的团簇式单元电子数CVE存在简单线性关系,由此可通过合金的电子浓度来确定合金的硬度.[(Cu4Ni12)Fe192](Cr32Ni8.5Mo2Ti2Nb0.5Al1V1)合金(Fe-8.82Ni-11.62Cr-1.34Mo-0.67Ti-0.32Nb-0.19Al-0.36V-1.78Cu,质量分数,%)具有高硬度和高强度(硬度值为488,σ0.2=1456 MPa,抗拉强度σb=1494 MPa)的同时,具有良好的拉伸塑性[52].因此,团簇成分式设计方法为多组元超高强度不锈钢提供了一种设计思路.

图5 (网刊彩色) [Ni-Fe12]Cr3团簇结构模型[52]孤立团簇[Ni-Fe12]按照类FCC单胞堆垛,连接原子Cr(白色球)占据四面体和八面体间隙位置,红色球代表团簇中心Ni原子,白色小球代表团簇壳层基体原子FeFig.5.(color online)[Ni-Fe12]Cr3cluster structure model[52]. [Ni-Fe12]clusters are packed according to an FCC-like pattern with glue Cr atoms(whitespheres)both in tetrahedral and octahedral interstices.Red spheres represent Ni atoms in the cluster center,and small white spheres are Fe atoms in the cluster shell.

此外,根据团簇结构模型研究了Ni基高温合金的成分规律,尽管该类合金中含有更多种类的合金化元素,可将这些元素进行分类,分别为Al系、Cr系和Ni系,进而建立团簇成分式[Al-Ni12](Al,Cr)x,此项工作正在进展中.

3.2.2 BCC固溶体合金

3.2.2.1 多组元Ti合金

以低模量β-Ti合金为例详细介绍团簇成分式的设计步骤.

步骤一根据使役性能确定添加元素.这类合金在设计过程中必须同时满足BCC-β结构稳定性要求和低弹性模量E,且生物医用合金要求无毒性元素添加.可添加的元素主要有Mo,Nb,Ta,Zr和Sn,β结构稳定元素Mo,Nb和Ta会提升合金的E,低模量元素Zr和Sn会使β结构失稳,因此需要同时添加这两类元素.

步骤二构建局域团簇结构单元和团簇成分式.根据溶质元素与基体Ti之间的混合焓大小,Mo和Sn与Ti之间的ΔH为负[47],则其位于团簇心部,Nb和Ta与Ti之间的ΔH为正,则其位于连接位置,Zr与Ti为同族元素,可替代基体Ti,从而形成BCC团簇成分式[(Mo,Sn)-(Ti,Zr)14](Nb,Ta)x.对现已报道的低弹性模量β-Ti合金成分解析发现基本满足连接原子x=1,3,5[53],这是由于不同合金化元素对β的稳定能力不同造成的.

步骤三实验验证.对[(Mo,Sn)-(Ti,Zr)14]Nbx系列合金的实验验证结果表明,合金的弹性模量与β结构稳定性和第二相(α′′,ω)密切相关. 当连接原子x=1时,[(Mo0.5Sn0.5)(Ti13Zr1)]Nb1合金在确保β结构稳定的同时,具有最低的弹性模量E=48 GPa[53].围绕该合金进一步进行成分微调,发现该合金仍为具有最低弹性模量的β-Ti合金.

步骤四结构稳定性表征.合金的弹性模量和析出相都与合金的β结构稳定性相关,因此借助二元Ti-M相图中Ti处的特殊成分点,如偏析点、共析点等(图6(a)),来考量合金化元素M对β结构稳定能力的影响.在富Ti处的[β/(α+β)]相界,即从纯Ti至Ti-M特殊成分点可知,不同的合金化元素用不同的含量可将β结构稳定在不同温度下,即该相界斜率可代表合金化元素M对β结构的稳定能力.因此,以Ti-Mo相图中的[β/(α+β)]相界斜率为标准,将其他Ti-M相图中的相界斜率与标准的比值作为Mo当量中合金化元素M的当量系数,从而得到新的Mo当量公式为meQ(Mo)=1.0m(Mo)+1.25m(V)+0.59m(W)+0.28m(Nb)+0.22m(Ta)+1.93m(Fe)+1.84m(Cr)+1.50m(Cu)+2.46m(Ni)+2.67m(Co)+2.26m(Mn)+0.30m(Sn)+0.47m(Zr)+3.01m(Si)-1.47m(Al)(质量分数,%)[53],且β结构稳定的最低下限Mo当量为11.8%(对应原子数分数为6.25%).与传统实验Mo当量值[2]相比,这个新的Mo当量在表征结构稳定性方面更具可靠性,如图6(b)所示,能够将现有报道的低模量β-Ti合金都涵盖在β稳定的最低下限以上[54].通常具有使β结构稳定的最低下限Mo当量的合金才具有低的弹性模量,Mo当量通常位于β稳定下限处βC,但在多组元体系中,最低模量β-Ti合金成分[(Mo0.5Sn0.5)(Ti13Zr1)]Nb1的meQ(Mo)=13.6%,略高于β稳定下限,以此来抑制第二相α′′和ω相的析出.

图6 (a)Ti-Mo二元相图[55];(b)弹性模量E和Mo当量关系图[54]Fig.6.(a)The Ti-Mo binary phase diagram[55];(b)the variation of Young’s modulus with Mo equivalent[54].

对于工程用Ti合金[56]而言,无论是α-Ti(HCP),(α + β)-Ti还是β-Ti合金,其在高温下都为单相β结构,且采用相同的合金化元素,只是为获得不同的结构而添加的含量不同.可根据团簇成分式设计方法建立成分通式[(Al,Sn,Cr,Fe)-(Ti,Zr)14](Mo,Nb,Ta)x,在此基础上,合金的结构稳定性由meQ(Mo)进行控制.图7为典型工程Ti合金在常规工艺条件下的抗拉强度σb与团簇成分式原子总数Z及meQ(Mo)之间的关系,可以看出抗拉强度高的Ti合金尽管结构不同,但合金的成分式原子总数Z大都集中于16-17之间,且抗拉强度随meQ(Mo)增加而增加,即β-Ti合金通常具有高的抗拉强度.表1列出了三类典型的高性能Ti合金的团簇成分式解析及meQ(Mo),分别为高温近α-Ti合金,高强韧(α+β)-Ti和高强β-Ti合金,可以看出,Z随meQ(Mo)的增大逐渐增大,这是由于α稳定元素Al含量基本不变,需要添加的β稳定元素含量逐渐增多,从而使Z逐渐增大.例如,工程用高温近α-Ti合金需要在600°C以上服役,要求合金具有优异的抗氧化性能和综合力学性能,为达到使役性能要求,在其中添加多种合金化元素,如Al,Mo,Nb,Si,Sn,Zr,Y,Ce,Nd等.这类合金组织为等轴α和片层β转变组织,故采用高温单相BCC固溶体团簇成分式来解析这类合金的成分,发现典型合金的团簇成分式中连接原子的个数x=0.8-1.2.典型600°C高温下合金Ti1100(Ti-6Al-2.75Sn-4Zr-0.4Mo-0.45Si,质量分数,%)的团簇成分式为[Al-(Ti13.67Zr0.33)](Al0.69Sn0.17Mo0.03Si0.12),连接原子个数x=1.02,恰对应BCC固溶体团簇最密堆垛的结构模型,即连接原子x=1的情形.在此团簇成分式基础上,利用相似元素等比例替换原则添加更多微量元素(Hf,Ta,Nb)共同合金化,设计的[Al-(Ti13.7Zr0.15Hf0.15)](Al0.69Sn0.18Si0.12Ta0.015Nb0.015)合金具有优异的抗高温氧化性能,在800°C下经100 h高温氧化后,该合金的氧化增重从Ti1100的13.6 mg/cm2降低至2.6 mg/cm2,氧化层厚度也由150 mm降低至24 mm,并且在质量分数为3.5%的NaCl溶液中的耐腐蚀能力明显提高[57].团簇成分式设计方法能够使高性能工程Ti合金的设计更加简单高效.

图7 工程Ti合金的抗拉强度σb与(a)团簇成分式原子个数Z及(b)Mo当量的关系[56]Fig.7.Correlations of tensile strengthσbwith(a)the total atom numberZof the cluster unit formula and(b)the Mo equivalent in industrial Ti alloys[56].

表1 典型工程Ti合金牌号成分及其团簇成分式和Mo当量值[56]Table 1.Compositions,corresponding cluster formulas andmeQ(Mo)of typical industrial Ti alloys[56].

3.2.2.2 多组元Zr合金

根据低模量β-Ti合金的成分设计步骤,在Zr-Mo-Sn-Ti-Nb体系中获得了低模量、 低磁导率的β-Zr合金[58]. 团簇成分式与β-Ti合金相同,为[(Mo,Sn)-(Zr,Ti)14]Nbx,其中x=1时合金具有优异的综合性能,如[(Mo0.5Sn0.5)-Zr14]Nb1(Zr-6.29Nb-3.25Mo-4.02Sn,质量分数,%)和 [(Mo0.5Sn0.5)-(Zr13Ti1)]Nb1(Zr-6.48Nb-3.34Ti-3.35Mo-4.14Sn,质量分数,%),合金的磁化率χ=2.12×10-6-2.13×10-6cm3·g-1, 为相同测试条件下纯Zr金属的85%,弹性模量E=77-79 GPa.

与低磁导率β-Zr合金不同,核燃料包壳材料用Zr合金中添加的溶质元素(Sn,Nb,Fe,Cr等)的总量一般小于3%(质量分数),属于稀固溶体合金范畴.为此,我们借助超高强度马氏体时效不锈钢的设计原则,将BCC固溶体团簇成分式[MZr14]M1自洽放大,得到超团簇式{[M-Zr14]M-([Zr-Zr14]Zr)12}([M-Zr14]M)3(式中原子个数为256个,M代表溶质原子),以体现微量合金化元素的添加含量.则合金化溶质元素M的总含量最多可以为8/256,即原子数分数为3.13%.根据合金化元素与基体Zr的交互作用,得到位于团簇中心的溶质元素(Sn,Fe,Cr)所能添加的最大含量上限为4/256(原子数分数为1.56%),连接位置Nb元素的最大添加含量也为4/256(原子数分数为1.56%).为进一步提升目前Zr合金包壳材料的耐蚀性能,在Zr-Sn-Nb-Fe-Cr-Cu合金体系中设计获得了低Sn含量的Zr合金系列,在高压釜腐蚀环境中表现出优异的耐蚀性能[10].例如,Zr-(0.5/256)Sn-(2/256)(Fe+Cr)-(1/256)Nb(原子分数,%)合金在360°C/18.6 MPa、质量分数为7×10-5的LiOH溶液中腐蚀283天的腐蚀增重为48 mg·dm-2,而同等条件下测试现有Zr合金(N36,Zr-1.0Sn-0.25Fe-1.0Nb,质量分数,%)的腐蚀增重为93 mg·dm-2. 低Sn含量Zr合金腐蚀增重仅为N36合金的一半,且前者的力学性能优异,抗拉强度σb=461 MPa.提高Nb含量可进一步提升Zr-(0.5/256)Sn-(2/256)(Fe+Cr+Cu)-(3/256)Nb(原子分数,%)合金力学性能,其σb=493 MPa,且同样具有优异的耐蚀性能,合金在360°C/18.6 MPa,Li+质量分数为7×10-5的溶液中腐蚀283天后腐蚀增重为68 mg·dm-2.

3.2.2.3 铁素体不锈钢

由于Zr合金包壳材料只能用于350°C以下,日本福岛核电站事故的发生使耐损伤容限(ATF)铁素体不锈钢成为研究的热点.Fe-Cr-Al系铁素体不锈钢不仅具有Zr合金的优异耐蚀性、低中子辐照敏感性等优点,还具有优异的抗高温氧化性和短时高温强度.现有研究表明,能够使耐蚀性和抗高温氧化性能达到最佳的基础合金成分为Fe-13Cr-4.5Al(质量分数,%),具有单一BCC结构[59].根据组元间的混合焓,Fe,Cr与Al均为强交互作用,且Fe和Cr之间交互作用很弱,在铁素体不锈钢中可相互替换,故在BCC结构中可建立[Al-(Fe,Cr)14]团簇,则基础合金成分满足团簇成分式[Al-(Fe12Cr2)](Al0.5Cr0.5).在此成分式基础上,添加微量Mo,Nb,Ti,Zr,Ta等合金化元素,以期析出具有高稳定性的Fe2M型Laves相,在1000°C以上的高温下有效钉扎铁素体基体晶界,防止基体晶粒长大,从而提升短时高温力学性能.初步研究表明,在1200°C高温回溶2 h,Zr/Ta微合金化的合金中仍有Laves相分布于晶界上,抑制了基体晶粒长大,此项工作正在进展中.

我们分析了现有不同合金体系中BCC基的工程牌号合金,发现大部分工程合金的成分(表2)均满足[CN14团簇](连接原子)x的团簇成分式,且连接原子x=1的成分式最为普遍.由此表明连接原子x=1的团簇成分式应为BCC固溶体合金的一种特殊稳定结构,满足这种结构的合金应具有优异的综合性能.

表2 典型BCC基工程合金牌号成分及其团簇式Table 2.Compositions and corresponding cluster formulas of typical BCC-based industrial alloys.

3.2.3 高熵合金

高熵合金是以多个元素(通常五元及以上)共同为基体的一类新型特殊合金.组成元素为等物质的量或近等物质的量比例添加,使得合金的热力学混合熵远高于传统合金,易于形成具有简单结构的固溶体相,也称为多主元固溶体合金,是目前科学研究的热点[67,68].这类合金多形成于Al-TM体系中,通过改变Al元素的含量来获得不同结构的高熵合金,其中TM多为等物质的量比例混合,可表示为AlxTMn(n为过渡金属元素的个数).由于Al与多数TM的相互作用相似,若将所有TM平均化为一个伪元素M,则Al元素变为由M作为基体元素的溶质元素,从而形成常规固溶体合金AlxMn.由此,我们利用团簇结构模型系统研究了Al-Co-Cr-Fe-Ni合金体系中高熵合金的组织结构及性能演变,发现团簇成分式[Al-M14]Al1恰对应该体系中FCC高熵合金形成的上限[69],且Al含量高于此团簇式给定的成分时,BCC相将从FCC基体中析出.当固定Al含量不变,改变TM的含量,也可使合金结构发生变化.通常BCC基的高熵合金具有高的强度,但是增加Al含量获得的BCC基高熵合金的组织多为BCC/B2的调幅分解状(B2为BCC固溶体的有序超结构),严重降低了合金的塑性,其室温拉伸塑性几乎为零[70].在确保合金高强度特性的同时,为改善合金的塑性,我们在团簇成分式[Al-M14]Al1基础上改变M的比例,选用M为Co1/5Cr1/5Fe2/5Ni1/5,获得的高熵合金基体为BCC/B2结构.最重要的是,通过调整BCC和B2相之间的点阵错配,获得了棋盘状B2纳米粒子与BCC基体共格的微观组织,如图8所示.这种组织与Ni基高温合金相同,有望应用于高温环境中,且该合金具有高的拉伸强度(σb=1223 MPa)和良好的塑性(δ=7.9%),拉伸后大量位错产生于BCC内部,且终止在BCC/B2界面上(图8(b)).

图8 [Al-M14]Al1(M：Co1/5Cr1/5Fe2/5Ni1/5)高熵合金透射电子显微镜形貌[69](a)拉伸前暗场像;(b)拉伸后明场像Fig.8.Transmission electron microscopic morphologies of[Al-M14]Al1(M：Co1/5Cr1/5Fe2/5Ni1/5)highentropy alloy[69]：(a)The dark-field image before tension;(b)the bright-field image after tension.

3.2.4 亚稳合金

亚稳合金主要包括非晶合金和准晶合金.非晶合金又称金属玻璃,是在快速凝固过程中原子来不及扩散形成的长程无序合金[71].研究表明具有强玻璃形成能力的块体非晶合金通常形成于多组元合金体系中,且成分敏感.由于非晶合金的结构为无定形态,目前提出了很多种结构模型用于理解非晶合金展现的特殊性能,其中大多数都基于局域短程有序的团簇结构[8].事实上,非晶合金中存在的溶质元素的局域短程有序与固溶体合金中溶质化学短程序是相同的,因此一直以来,本课题组都采用团簇加连接原子结构模型来设计块体非晶合金.不同之处在于,非晶合金的短程拓扑有序和化学有序使得成分设计中更要注重对团簇结构的选取,根据合金体系的不同可以选择具有不同配位数的团簇结构,如CN9-CN14[8,72-75];而在固溶体结构中,团簇结构只有CN12和CN14,取决于固溶体结构类型.另外,具有强玻璃形成能力的块体非晶合金的团簇成分式中连接原子个数通常固定,为x=1或3;而在固溶体合金团簇成分式中连接原子个数会随合金结构稳定性及性能改变而变化[9,10,53].以典型Cu-Zr基非晶为例[8],在与非晶竞争的Cu8Zr3相中选取最密堆二十面体团簇[Cu-Cu7Zr5],当[Cu-Cu7Zr5]团簇连接一个Cu原子时形成成分式[Cu-Cu7Zr5]Cu1(Cu64.3Zr35.7),此合金在Cu-Zr二元体系中具有最强的玻璃形成能力;当连接原子变为M(M为Al,Ag,Ti,Nb,Ta,Mo)时,获得的三元Cu基Cu-Zr-M也具有最强的玻璃形成能力[72];当添加更多组元时,可采用相似组元替代法依次取代团簇心部、团簇壳层和连接位置处的原子,以此发展具有更强玻璃形成能力的块体非晶合金[73].进一步对其他非晶合金体系(包括Ti基、Ni基、Fe基、Al基、Pd基等)的最佳块体非晶合金[73-75]进行研究表明,最佳块体非晶合金成分基本满足[团簇](连接原子)1,3的团簇式,即x=1或3.在此基础上发展出团簇球周期共振模型,用以解释最佳块体非晶合金成分的内在含义,如图9所示,即理想块体非晶团簇成分式包含电子数为24,即合金的电子浓度为24/Z(Z为团簇成分式中原子个数).

图9 (网刊彩色)团簇共振模型示意图[73]Fig.9. (color online)Schematic of the clusterresonance model[73].

以Ti-Cu基体为例介绍利用团簇成分式方法设计块体非晶合金的步骤[75].

步骤一选择具有潜在高玻璃形成能力的成分区,通常位于两个金属间化合物相构成的共晶区.在Ti-Cu二元基础相图中,存在两个此类型共晶点Cu73Ti27和Cu43Ti57(原子数分数,%),对应的晶体相分别为(Cu2Ti+Cu4Ti)和(CuTi2+CuTi).Ti-Cu体系可形成非晶的成分范围是Cu28Ti72到Cu75Ti25,此成分区间主要覆盖CuTi2和CuTi相构成的共晶区域.

步骤二确定晶化析出相.根据退火和快淬的实验结果确定与非晶形成相关的晶化析出相为Cu2Ti(MoSi2型结构,tI6)和CuTi(CuTi型结构,tP4).

步骤三根据团簇的孤立度和密堆度确定主团簇. 根据原子密度的径向分布,可以确定CuTi2相结构有两种团簇构型[Cu-Ti8Cu4]和[Ti-Cu4Ti8],其中前者中心原子与壳层原子的半径比R[Cu-Ti8Cu4]=0.914更接近于理想CN12团簇的比值(R∗≈0.902);而在CuTi相结构中确定[Cu-Cu8Ti6]和[Ti-Cu6Ti8]团簇,其中后者R[Ti-Cu6Ti8]=1.056接近理想CN14团簇的比值(R∗≈1.047).此处由于两种共晶相的团簇均存在严重的原子共享,其孤立度较低并且差异较小,因此以团簇的密堆程度作为主要衡量标准,最终确定Cu2Ti和CuTi相的主团簇分别为[Cu-Ti8Cu4]和[Ti-Cu6Ti8].

步骤四构建团簇成分式.以主团簇加1或3个连接原子构建团簇式,根据电子浓度规则确定理想非晶成分.分别以Ti3,Ti,CuTi2,Cu2Ti,Cu和Cu3作为连接原子,结合两个共晶相的主团簇构建成分式,在所有团簇成分式中挑选满足24电子数的成分式,从而确定基础二元团簇式[Ti-Cu6Ti8]Cu3(团簇式电子浓度e/u=23.6),代表了该成分区间的理想非晶合金成分.

步骤五采用相似原子替换原则获得具有高玻璃形成能力的非晶合金.最后通过相似元素替换团簇式中心、壳层以及连接位置的原子(Zr部分替换Ti,Sn部分替换Cu),得到具有强非晶形成能力(临界尺寸为5 mm)的块体非晶合金Ti40Zr10Cu56.94Sn3.06(原子数分数,%).

准晶合金是一种同时具有长程准周期平移序和非晶体学旋转对称性的金属间化合物.其原子呈定向有序排列,原子结构不能由某一结构单元在三维空间周期性重复排列得到,主要存在于Al基合金体系中.准晶类似相与准晶具有相同的局域二十面体短程序,由此建立准晶的团簇式为[二十面体团簇](连接原子)x[8].以Al-Cu-Co体系为例[76],其准晶形成由Al-Co系团簇和Al-Cu系团簇共同决定.与Al-Co之间较大的负混合焓[47](ΔHAl-Co=-19 kJ/mol)相比,Al-Cu和Cu-Co之间呈现较弱的相互作用(ΔHAl-Cu=-1 kJ/mol,ΔHCu-Co=6 kJ/mol).从二元Al-Co十次准晶基础团簇式[Co-Co2Al10]Co1(图10)出发,利用3个Cu原子分别替换二十面体团簇[Co-Co2Al10]壳层位置的2个Co原子和1个Al原子,得到团簇成分式[Co-Cu3Al9]Co1为Al64.3Cu21.4Co14.3(原子数分数,%). 团簇式给出的成分与实验成分Al64.3Cu21.9Co13.8几乎重合,成分偏差仅为0.7%(原子数分数),与另外一个实验成分Al66Cu19Co15的偏差为3.1%(原子数分数)[76].此外,根据团簇共振结构模型和直接赋值法从价电子浓度角度分析准晶的形成规律,发现理想二元和三元准晶合金的单元团簇成分式包含的价电子数目也满足24电子数准则,且设计步骤与非晶相同.

基于团簇结构模型的合金设计方法可应用于不同的复杂合金体系中,通过合金化元素与基体元素之间的相互作用,可确定合金化元素在团簇成分式中的位置及添加含量,从而设计出具有优良性能的多元合金成分.团簇成分式设计方法在多种合金体系中的应用体现出该方法的普适性,能够为多元合金成分设计提供一种简单、精确的途径.

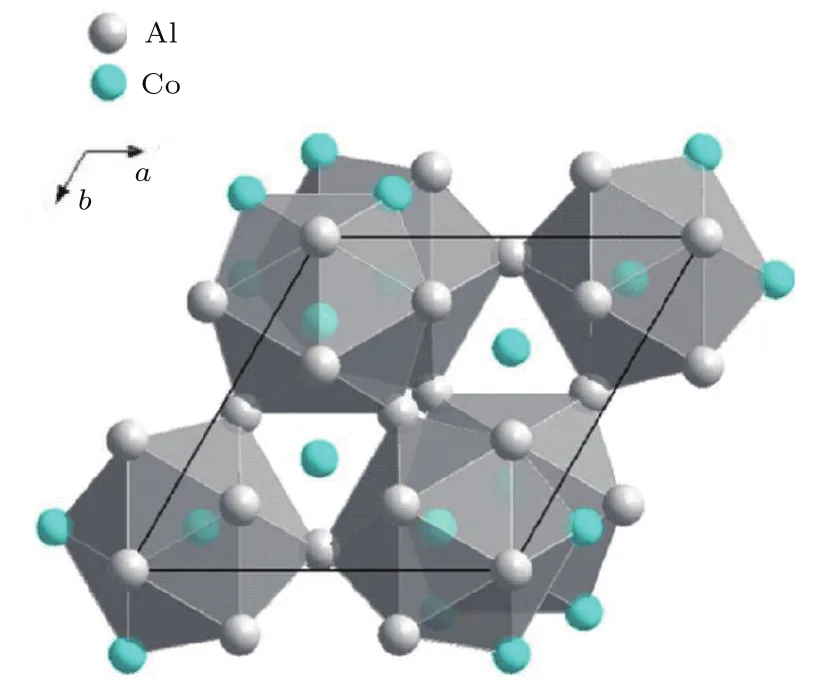
图10 (网刊彩色) 二十面体[Co-Co2Al10]团簇的空间排布[76]Fig.10.(color online)The spatial packing of icosahedral[Co-Co2Al10]clusters[76].

4 结 论

在对多元合金化机理不断探索的过程中,人们通过大量实验得到了诸多行之有效的合金成分设计方法,如预测合金化元素固溶度的Hume-Rothery规则、表征合金结构稳定性的当量法、合金性能的直接计算模拟等,这些都为复杂合金材料的研发提供了指导,但无法从根本上建立基本单元元素组合-组织结构-基本性质之间的内禀关系.基于固溶体局域短程序结构的团簇成分式设计方法,考虑了基本单元元素之间的交互作用,建立在”团簇加连接原子”稳定固溶体结构模型基础之上,该方法在诸多复杂合金体系(Cu合金、特种不锈钢、Ti合金、Zr合金、高熵合金、亚稳合金、高温合金)中的成功应用验证了其普适性,为多元复杂合金成分设计提供了一种简单而精确的方法.在针对具体使役性能确定具体合金设计步骤的过程中,在团簇成分式基础上引入了其他因素,如当量、错配度等,以实现对结构和组织的控制,由此获得期望的性能,这部分工作仍需进一步完善,希望借助该方法最终实现成分-组织-性能之间的关联.

[1]Hume-Rothery W,Raynor G V 1940Proc.R.Soc.London,Ser.A Math.Phys.Sci.174 471

[2]Bania P J 1994Jom.46 16

[3]Bagariatskii I A,Nosova G I 1958Sov.Phys.Dokl.3 1014

[4]Morinaga M,Yukawa N,Adachi H 1985J.Phys.F15 1071

[5]Ghosh G,Asta M 2005Acta Mater.53 3225

[6]Xu W,Rivera-Díaz-del-Castillo P E J,Yan W,Yang K,San Martín D,Kestens L A I,van der Zwaag S 2010Acta Mater.58 4067

[7]Malinov S,Sha W 2004Mater.Sci.Eng.A365 202

[8]Dong C,Wang Q,Qiang J B,Wang Y M,Jiang N,Han G,Li Y H,Wu J,Xia J H 2007J.Phys.D:Appl.Phys.40 R273

[9]Hong H L,Wang Q,Dong C,Liaw P K 2014Sci.Rep.4 7065

[10]Pang C,Jiang B,Shi Y,Wang Q,Dong C 2015J.Alloys Compd.652 63

[11]Darken L S,Gurry R W 1953Physical Chemistry of Metals(New York：McGraw-Hill Co)pp258-266

[12]Gschneidner K A 1964Solid State Phys.16 275

[13]Chelikowsky J R 1979Phys.Rev.B19 686

[14]Alonso J A,Simozar S 1980Phys.Rev.B22 5583

[15]Zhang B W,Liao S Z 1996Z.Phys.B99 235

[16]Inoue A 2000Acta Mater.48 279

[17]Zhang Y,Zuo T T,Tang Z,Gao M C,Dahmen K A,Liaw P K,Lu Z P 2014Prog.Mater.Sci.61 1

[18]Hume-Rothery W 1966Acta Metall.14 17

[19]Hao Y L,Li S J,Sun S Y,Zheng C Y,Yang R 2007Acta Biomater.3 277

[20]Guo S,Ng C,Lu J,Liu C T 2011J.Appl.Phys.109 103505

[21]Hall E O,Algie S H 1966Metall.Rev.11 61

[22]Zhang J S,Cui H,Hu Z L,Murata Y,Morinaga M,Yukawa N 1993Acta Metall.Sin.29 289(in Chinese)[张济山,崔华,胡壮麟,村田纯教,森永正彦,汤川夏夫1993金属学报29 289]

[23]Abdel-Hady M,Hinoshita K,Morinaga M 2006Scripta Mater.55 477

[24]Chen H,Ding T S,Wang T,Xiao X S,Zhao J L,Jiang L Z 2010Rare Metal.Mat.Eng.39 386(in Chinese)[陈宏,丁铁锁,王涛,肖学山,赵钧良,江来珠 2010稀有金属材料与工程39 386]

[25]Saito T,Furuta T,Hwang J H,Kuramoto S,Nishino K,Suzuki N,Chen R,Yamada A,Ito K,Seno Y,Nonaka T,Ikehata H,Nagasako N,Iwamoto C,Ikuhara C,Sakuma T 2003Science300 464

[26]Kuroda D,Niinomi M,Morinaga M,Kato Y,Yashiro T 1998Mater.Sci.Eng.A243 244

[27]Yu R H 1978Chin.Sci.Bull.13 217(in Chinese)[余瑞璜1978科学通报13 217]

[28]Liu Z L,Lin C 2006Prog.Nat.Sci.16 78

[29]Cai J Y,Peng J Z,Yang X Z,Gray M F 2008Mater.Lett.62 3957

[30]Pang X M,Zheng Y,Wang S G,Wang Q H 2009Int.J.Refract.Met.Hard Mater.27 777

[31]Okazaki Y,Gotoh E 2005Biomaterials26 11

[32]Rosenberg H W,Jaffee R I 1970The Science,Technology and Application of Titanium(Oxford：Pergamon Press)p851

[33]Schaeffler A L 1949Met.Prog.56 680

[34]Morachevskii A G 2001Russ.J.Appl.Chem.74 1610

[35]Ferjutz K,Davis J R 1993ASM Handbook,Volume 6:Welding,Brazing and Soldering(The USA：ASM International)p1009

[36]Morishita K,Sugano R,Wirth B D,Diaz de la Rubia T 2003Nucl.Instrum.Methods Phys.Res.Sect.B202 76

[37]Lee N T S,Tan V B C,Lim K M 2006Appl.Phys.Lett.88 031913

[38]Holland J H 1992Sci.Am.267 66

[39]Ikeda Y 1997Mater.Trans.JIM38 771

[40]Zeng W D,Shu Y,Zhou Y G 2004Rare Metal.Mat.Eng.33 1041(in Chinese)[曾卫东,舒滢,周义刚2004稀有金属材料与工程33 1041]

[41]Reddy N S,Lee Y H,Park C H,Lee C S 2008Mater.Sci.Eng.A492 276

[42]Damask A C 1956J.Appl.Phys.27 610

[43]Butt M Z,Ghauri I M 1988Phys.Stat.Sol.107 187

[44]Reinhard L,Schönfeld B,Kostorz G,Bührer W 1990Phys.Rev.B41 1727

[45]Cowley J M 1960Phys.Rev.B120 1648

[46]Häussler P 1992Phys.Rep.222 65

[47]Takeuchi A,Inoue A 2005Mater.Trans.46 2817

[48]Zhang J,Wang Q,Wang Y M,Li C Y,Wen L S,Dong C 2010J.Mater.Res.25 328

[49]Zhang J,Wang Q,Wang Y M,Wen L S,Dong C 2010J.Alloys Compd.505 179

[50]Zhang X Y,Li X N,Nie L F,Chu J P,Wang Q,Lin C H,Dong C 2011Appl.Surf.Sci.257 3636

[51]Li B Z,Gu J J,Wang Q,Ji C J,Wang Y M,Qaing J B,Dong C 2012Mater.Charact.68 94

[52]Wang Q,Zha Q F,Liu E X,Dong C,Wang X J,Tan C X,Ji C J 2012Acta Metall.Sin.48 1201(in Chinese)[王清,查钱锋,刘恩雪,董闯,王学军,谭朝鑫,冀春俊 2012金属学报48 1201]

[53]Wang Q,Ji C J,Wang Y M,Qiang J B,Dong C 2013Metall.Mater.Trans.A44 1872

[54]Wang Q,Dong C,Liaw P K 2015Metall.Mater.Trans.A46 3440

[55]Murray J L 1992ASM Handbook,Volume 3:Alloy Phase Diagrams(The USA：ASM International)p1156

[56]Welsch G,Boyer R,Collings E W 1993Materials Properties Handbook:Titanium Alloys(The USA：ASM International)pp439-921

[57]Che J D,Jiang B B,Wang Q,Dong C,Chen G Q,Zhang R Q,Tang R 2016Rare Metal.Mat.Eng.(in press)(in Chinese)[车晋达,姜贝贝,王清,董闯,陈国清,张瑞谦,唐睿2016稀有金属材料与工程(已接收)]

[58]Pang C,Wang Q,Zhang R Q,Li Q,Dai X,Dong C,Liaw P K 2015Mater.Sci.Eng.,A626 369

[59]Yamamoto Y,Pint B A,Terrani K A,Field K G,Yang Y,Snead L L 2015J.Nucl.Mater.467 703

[60]Kondo R,Nomura N,Tsutsumi Y,Doi H,Hanawa T 2011Acta Biomater.7 4278

[61]Zhao W J,Miao Z,Jiang H M,Yu X W,Li W J,Li C,Zhou B X 2002J.Chin.Soc.Corros.Rrot.2 61(in Chinese)[赵文金,苗志,蒋宏曼,于晓卫,李卫军,李聪,周邦新2002中国腐蚀与防护学报2 61]

[62]Jeong Y H,Lee K O,Kim H G 2002J.Nucl.Mater.302 9

[63]Park J Y,Choi B K,Yoo S J,Jeong Y H 2006J.Nucl.Mater.3 59

[64]Park J Y,Choi B K,Jeong Y H,Jung Y H 2005J.Nucl.Mater.340 237

[65]Jeong Y H,Kim H G,Kim T H 2003J.Nucl.Mater.37 1

[66]Smith D L,Chung H M,Loomis B A,Matsui H,Votinov S,Van Witzenburg W 1995Fusion.Eng.Des.29 399

[67]Senkov O N,Miller J D,Miracle D B,Woodward C 2015Nature Comm.6 7529

[68]Gludovatz B,Hohenwarter A,Catoor D,Chang E H,George E P,Ritchie R O 2014Science345 1153

[69]Wang Q,Ma Y,Jiang B B,Li X N,Shi Y,Dong C,Liaw P K 2016Scripta Mater.120 85

[70]Zhi T,Yuan T,Tsai C W,Yeh J W,Lundin C D,Liaw P K 2015Acta Mater.99 247

[71]Klement W,Willens R H,Duwez P O L 1960Nature187 869

[72]Luo L J,Chen H.,Wang Y M,Qiang J B,Wang Q,Dong C,Häussler P 2014Philos.Mag.94 2520

[73]Han G,Qiang J,Li F,Yuan L,Quan S G,Wang Q,Wang Y M,Dong C,Häussler P 2011Acta Mater.59 5917

[74]Geng Y X,Wang Y M,Qiang J B,Zhang G F,Dong C,Haussler P 2016J.Non-Cryst.Solids.432 453

[75]Wang Z R,Qiang J B,Wang Y M,Wang Q,Dong D D,Dong C 2016Acta Mater.111 366

[76]Chen H,Qiang J B,Wang Y M,Dong C 2014Acta Phys.Pol.A126 446

PACS:61.66.Dk,61.72.Bb,81.30.-t,62.20.-x DOI:10.7498/aps.66.026102

A cluster-formula composition design approach based on the local short-range order in solid solution structure∗

Jiang Bei-Bei Wang Qing†Dong Chuang
(Key Laboratory of Materials Modification by Laser,Ion and Electron Beams of the Ministry of Education,School of Materials Science and Engineering,Dalian University of Technology,Dalian 116024,China)

3 September 2016;revised manuscript

25 October 2016)

The composition design is of importance for developing high-performance complex alloys and is also the primary step to realize a new mode for material development via theoretical prediction and experimental verification,in comparison with the traditional experience-oriented experiments.Traditional alloy design approaches,including Hume-Rothery rule,electron theories,equivalent method,computer simulation,etc.,are first reviewed from the viewpoints of their theoretical basis and applicability to limitations.Almost all the traditional alloys are based on solid solution structures,in which the typical characteristic is the chemical short-range order(CSRO)of the solute distribution.We propose a cluster-plus-glueatom model for stable solid solutions in light of CSRO.A cluster-formula composition design approach is presented for developing the multi-component high-performance alloys.The cluster-plus-glue-atom model classifies the solid solution structure into two parts,i.e.,the cluster part and the glue atom part,where the clusters are centered by solute atoms,showing the strong interactions of clusters with the solvent base and the weak interactions of clusters with solute atoms.The clusters are the nearest-neighbor polyhedrons,being cuboctahedron with a coordination number of 12(CN12)in FCC structure and rhombic dodecahedron with a CN14 in BCC structure,respectively.Then a uniform cluster-formula of[CN12/14 cluster](glue atom)xis achieved from the cluster model.Its wide applications in different multi-component alloy systems confirm its universality as a simple and accurate tool for multiple-component complex alloy composition design.Such alloy systems include corrosion-resistant Cu alloys,high-performance Ni-base superalloys,high-strength maraging stainless steels,Ti/Zr alloys with low Young’s modulus,high-entropy alloys,amorphous metallic glasses,quasicrystals,etc..The specific alloy design steps are incarnated in the β-Ti alloys with low Young’s modulus.Firstly,the necessary alloying elements are chosen according to the service requirements(BCC stability and low Young’s modulus).Secondly,the local cluster unit to present CSRO and the corresponding cluster formula of[(Mo,Sn)-(Ti,Zr)14](Nb,Ta)xare built,in which the occupations of the alloying elements in the cluster formula are determined by the enthalpy of mixing ΔHbetween them with the base Ti.Thirdly,these designed alloys are verified experimentally,and the lowest Young’s modulus appears at the β-[(Mo0.5Sn0.5)-(Ti13Zr1)]Nb1.Finally,a new Mo equivalent formula under the guidance of phase diagram features is proposed to characterize the structural stability of Ti alloy.Thus all the Ti alloy compositions with different structural types can be expressed with a uniform cluster formula,in which the structural types of alloys are determined by the Mo equivalent.

composition design,multi-component alloys,cluster-plus-glue-atom model,solid solution

:61.66.Dk,61.72.Bb,81.30.-t,62.20.-x

10.7498/aps.66.026102

∗国家自然科学基金(批准号：51131002)、辽宁省自然科学基金(批准号：2015020202)、国际科技合作计划(批准号：2015DFR60370)、中央高校基本科研业务费专项资金(批准号：DUT16ZD212)和国家重点研发计划(批准号：2016YFB0701200)资助的课题.

†通信作者.E-mail：wangq@dlut.edu.cn

*Project supported by the National Natural Science Foundation of China(Grant No.51131002),the Natural Science Foundation of Liaoning Province of China(Grant No.2015020202),the International Science&Technology Cooperation Program of China(Grant No.2015DFR60370),the Fundamental Research Funds for the Central Universities(Grant No.DUT16ZD212),and the National Key Research and Development Plan(Grant No.2016YFB0701200).

†Corresponding author.E-mail：wangq@dlut.edu.cn