利用相干制备的三能级原子介质实现低噪声弱光相位操控∗

关佳 顾翊晟 朱成杰 羊亚平

(同济大学物理科学与工程学院,上海 200092)

利用相干制备的三能级原子介质实现低噪声弱光相位操控∗

关佳 顾翊晟 朱成杰†羊亚平‡

(同济大学物理科学与工程学院,上海 200092)

(2016年6月26日收到;2016年8月16日收到修改稿)

我们发现利用相干制备的三能级原子介质可实现低噪声弱光相位操控.基于两波混频效应,相干制备的原子系统在弱光相位操控方面有许多新特性,例如宽频范围内无损常数相位的实现以及无附加相位的吸收与放大等.通过同时锁定抽运光的光强和双光子失谐,我们发现探测光的吸收为零,且探测光的相位对于频率的变化十分缓慢,因而可以通过选择适当的系统参数在很宽的频率范围内实现无损π相位操控.同时,利用该系统我们可以在单光子水平下实现低噪声、无损的量子相位门,这个系统在光通信和信息处理领域有着重要的应用价值.

非线性光学,相干光学效应,量子噪声

1 引 言

近年来,由于信息科学的飞速发展,量子通信与量子计算成为了近代物理学研究的热门领域之一[1],而相位操控技术则是实现量子通信与量子计算的基础.随着激光器的诞生以及相干光与物质相互作用研究的不断深入,利用量子干涉效应/非线性光学效应在原子系统中实现单光子/少光子相位操控已成为十分有趣的新课题.尤其是电磁诱导透明(electromagnetically induced transparency,EIT)[2,3],利用抽运光导致的缀饰态之间的干涉效应减少介质对探测光的吸收,已在光与量子信息处理等方面得到了重要的应用,例如超慢光与光存储[4]、非线性相位门[5]、非线性偏振旋转门[6]等.虽然EIT可以通过量子干涉效应使探测光的群速度与相位都发生改变,但是探测光无法获得较大的相位变化(尤其是非线性相位),这是因为探测光需要传播较长的距离来积累足够大的相位,但是传播距离越长,探测光的衰减越明显,从而阻碍了探测光相位的增加.

为了克服EIT的这一缺点,人们提出了主动拉曼增益(active raman gain,ARG)系统[7,8],该系统的提出源于人们对快光与慢光的研究.与EIT系统不同,探测光不仅不会被介质吸收,同时还将获得一定的相干放大[9].不仅如此,ARG系统较EIT系统而言拥有许多崭新的特点,例如超光速现象[10]、交叉相位调制增强[11]、超快相位门与偏振旋转门[12,13]等.虽然ARG系统可以使探测光的相位达到π且探测光光强没有任何衰减,但这类系统却不适用于单光子/少光子量子通信与量子计算,这是因为在探测光被相干放大的同时,量子噪声也同样获得增强,这在量子信息的操控与处理方面是十分不利的.

基于EIT和ARG在实现相位操控方面的缺陷,我们提出了相干制备的三能级原子构型.相干制备态的概念可以追溯到激光科学产生的早期.早在1961年,Bell和Bloom[14]就提出在碱金属原子的塞曼能级之间可以产生相干态.1976年Alzetta等[15,16]发现激光的不同的纵模能够在碱金属原子的超精细基态间诱导产生类似的相干态.几乎在同一时间,Arimondo和Orriols[17]及Gray等[18]指出通过相干双光子跃迁可以实现无吸收原子态.这一研究引起了人们的广泛关注,近50年来关于此问题的研究十分活跃,一系列概念相继提出,相关实验研究层出不穷,例如相干布局俘获[19]、电磁诱导透明及无反转激光[20-24]等.在光波混频领域,相干制备态的技术被广泛应用于各种研究,比如克尔非线性移相增强[25,26]、暗态极化子[27]、非弹性四波混频[28]的产生以及时间-振幅-群速度匹配脉冲[29]等.

在本文中,我们研究发现相干制备的三能级原子系统具有简单的三能级EIT和ARG系统所没有的新特性,例如宽频范围内无损常数相位的实现、无附加相位的吸收与放大、完全透明等,这些新特性源于相干基态能级间的两波混频的过程[30].通过同时锁定抽运光光强与双光子失谐,探测光的吸收可以被完全抑制,并且在很宽的频率范围内获得一常数相位.在合适的系统参数下,该常数相位的大小可达π.不仅如此,我们还发现当探测光的光强处于单光子/少光子情况时,探测光的噪声也可以被抑制,从而实现极低噪声的无损量子相位门.

2 物理模型

我们讨论图1所示的新型Λ型三能级原子系统.图中|1〉和|3〉为超精细基态,|2〉为激发态.我们假设先将原子相干制备在两低能态上,然后再加入抽运场EP和探测场Ep.角频率为ωP的抽运场耦合|2〉和|1〉能级,角频率为ωp的探测场耦合|2〉和|3〉能级.我们定义Δ1=0,Δ2=δ=ωP-ω21(单光子失谐)和Δ3=δ2ph=ωP-ωp-ω31(双光子失谐),定义ħωi(i=1,2,3)表示|i〉态的本征能量.

在偶极近似和旋转波近似下,相互作用绘景中系统的哈密顿量由下式给出：

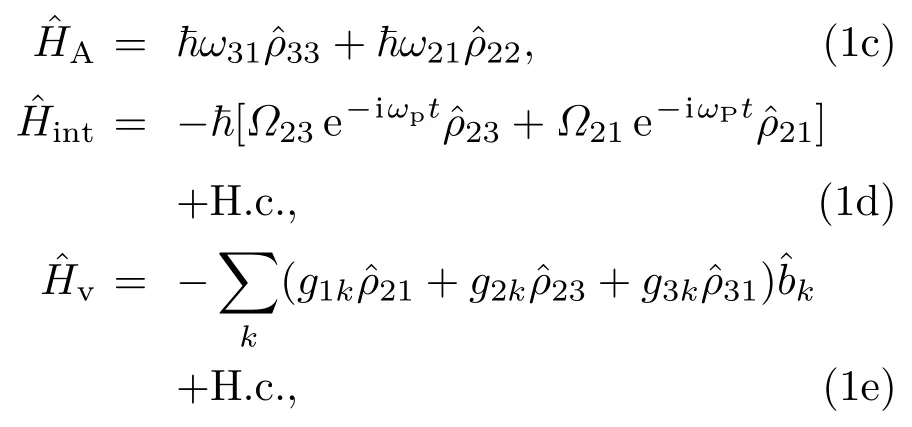
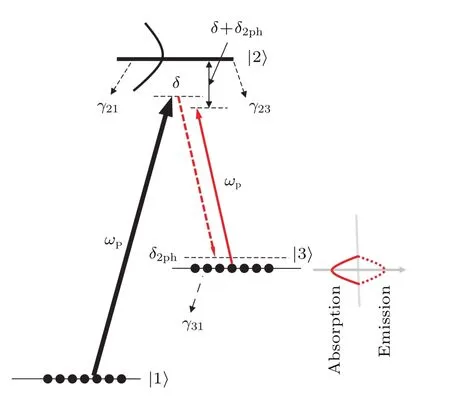
图1 (网刊彩色)新型三能级原子与探测场和抽运场作用的示意图 在强抽运场EP和弱探测场Ep加入之前我们要将原子相干制备在两低能态上;角频率为ωP的控制场耦合|2〉和|1〉能级,角频率为ωp的探测场耦合|2〉和|3〉能级;δ表示抽运光的单光子失谐量,δ2ph表示抽运光和探测光的双光子失谐量Fig.1.(color online)A three-level scheme where two lower states are coherently prepared prior to the injection of a strong pump fieldEPand a weak quantum probe fieldEp.In our scheme,the pump(probe)field with angular frequencyωP(ωp)drives the|2〉←→|1〉(|2〉←→|3〉)transition and the two lower states.δdescribes one-photon detuning andδ2phdescribes twophoton detuning.

结合系统的哈密顿量(1a),可得到原子算符演化的海森伯-郎之万运动方程如下：

其中C(0)=(iδ2ph+γ13)ρ33+i|Ω21|2ρ11/(δ-iγ23),B(0)=|Ω21|2+(-iδ2ph-γ13)(iδ-γ23)(这里我们假设δ≫δ2ph且γ23=γ21).从物理意义上来说,C(0)的第一项表示吸收过程源于|3〉能级,其第二项表示拉曼增益过程起始于|1〉能级.方程(6)包含许多新的物理性质,吸收与增益的强弱取决于抽运场/探测场以及失谐量的相对大小.

2.1 宽频域无损相位操控

为了研究此新型三能级原子系统所具有的特性,我们假设κIm[D(0)]=0,则方程(7)中Re[C0]Re[B0]+Im[C0]Im[B0]=0,因此可得

显然,若ρ33=0,即我们只将原子初始制备在基态|1〉,基态|3〉没有原子.此时方程(8)的解没有意义,这就体现了制备相干态的重要性.

利用求根公式,方程(8)的解X为

我们继续讨论方程(9),令ρ11=ρ33=ρ31=0.5,这是初态制备的条件.当ρ11=ρ33=0.5[30],同时ρ31的相干度取最大值0.5时,系统可达到一个最大的相干态,不仅有利于探测光的高效产生,而且可以降低拉曼过程导致的噪声.此时原子相干度最大,且

通常,单位相位传播距离φ=κRe[D(0)],利用方程(8)的假设 (即Im[D(0)]=0),Re[C0]=从而可得单位长度上的相位为

当Xδ＜δ2ph时,δ2phδ对分母起决定性作用,这种情况下方程(11)可简化为

(12)式表明在我们的系统中探测光的相位的变化与双光子失谐δ2ph无关.由于φ0中不显含δ2ph,因此探测光的相位与探测光频率无关,仅取决于单光子失谐的大小.这些特性都不可能在任何简单的三能级EIT系统或拉曼增益系统中实现.

图2(a)表示探测光相位和增益/损失随双光子失谐的变化.为了实现无损常数相位移动,我们取ρ11=ρ33=0.5,κ=3×1012s-1·m-1,γ21/(2π)=6 MHz,γ23/(2π)=6 MHz,γ31/(2π)=10 kHz,δ/(2π)=-1 GHz,Ω21/(2π)=30 MHz 以及L=1 cm.如图2(a)所示,同时锁定抽运场强和双光子失谐,在很大的双光子失谐范围内(即探测光的频率范围)探测光的相位为常数,且吸收/增益接近于零.不仅如此,系统产生的量子噪声也很小,下面我们会对此问题进行详细讨论.

图2(b)和图2(c)分别表示探测光相位和损失/增益随抽运场拉比频率与双光子失谐的变化.图3(c)的等高线表示探测光吸收为零,即探测场无损耗.显然,在很大的双光子失谐范围内,探测光的增益/损失为零,且其相位变化十分缓慢,几乎一直稳定于一个常数,在合适的系统参数下,该常数相位的大小可达π,从而实现了宽频域、无损耗、δ2ph无关的π相移操控.

图2 (网刊彩色)(a)探测光相位κRe[D(0)]L(红色实线)和损失/增益κIm[D(0)]L(蓝色虚线)关于双光子失谐δ2ph的函数变化图,保持方程(9)的锁定状态可实现无损耗常数相位;(b),(c)分别表示探测光相位和损失/增益随抽运场拉比频率以及双光子失谐的变化Fig.2.(color online)(a)Probe phase shiftκRe[D(0)]L(red solid-line)and the loss/gainκIm[D(0)]L(blue dashed-line)as a function of the two-photon detuningδ2ph,a flat zero gain/loss dispersion with a constant phase shift can be achieved by maintaining the locking condition Eq.(9);(b)and(c)display the contour plots of the probe phase shift and the loss/gain as functions of the pump field Rabi-frequency and the two-photon detuning,respectively.

2.2 无附加相位的吸收器与放大器

该系统不仅可以实现无损的π相移操控,还可用于实现其他经典的三能级EIT/ARG系统没有的新特性,比如无附加相位的吸收器与放大器.具体过程如下：令方程(7)的实部为零(Re[D(0)]=0)即Re[B0]Im[C0]-Im[B0]Re[C0]=0,可得

其解为

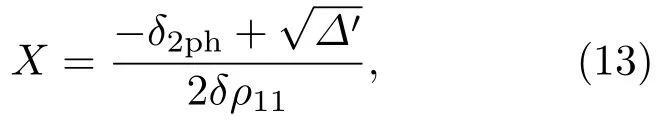
其中

从而系统的衰减系数可表示为

其中X是方程(13)的解.显然α＞0表示吸收,α＜0表示增益,因此想要实现无附加相位的衰减或放大取决于参数的选择.

图3(a)表示探测光相位和损失/增益随双光子失谐的变化.其中δ/2π=-400 MHz,其他参数和图2一致.如图所示,系统存在两个特殊的双光子失谐δ2ph(分别对应图中的垂直实线和虚线)可使探测光的相位(参见图中红色实线)为零,但探测光的吸收/增益(参见图中蓝色虚线)最大,也就是说探测场可实现无附加相位的吸收和放大.

图3 (网刊彩色)(a)探测光相位κRe[D(0)]L(红色实线)和损失/增益κIm[D(0)]L(蓝色虚线)关于双光子失谐的函数变化图,垂直的虚线和实线分别表示在零相位移动下可实现探测光衰减和放大;(b)和(c)分别表示探测光相位和损失/增益随双光子失谐和抽运场拉比频率的变化;水平虚线表示在我们的系统中可实现无附加相位的吸收器与放大器,垂直的绿色线表示抽运场拉比频率的选取Fig.3.(color online)(a)Probe phase shiftκRe[D(0)]L(red solid-line)and the loss/gainκIm[D(0)]L(blue dashed-line)versus the two-photon detuning,the vertical dashed-lines and solid-lines indicate significant probe attenuation and amplification without phase change;(b)and(c)display the contour plots of the probe phase shift and the loss/gain as functions of the two-photon detuning and the pump field Rabi-frequency,respectively.The horizontal dashed lines indicate the two-photon detuning to construct an attenuator or amplifier.The vertical dash-dotted line denotes the choice of the pump field Rabi-frequency.

图3(b)和图3(c)分别表示探测光相位和损失/增益随抽运场拉比频率和双光子失谐的变化.对于任意的抽运场拉比频率(参见图3(b)和(c)的绿色垂直线),总存在两个双光子失谐(参见水平线)可实现无附加相位的吸收器与放大器.

2.3 低噪声探测场移相器

最后,我们详细讨论系统实现宽频域无损π相位操控过程中的量子噪声问题.在慢变振幅近似和相位近似下,探测场拉比频率的麦克斯韦方程可表示为

通过求解麦克斯韦方程(15)和海森伯-郎之万方程(2),可得到延迟输出探测场[31,32],即

其中Λ=Λ(ω)=-i[ω/c+κD(ω)],(0,ω)是探测场初始位置算符.由于且g=代表探测场与原子的耦合常数,我们可以得到归一化输出的探测场：

通过引入归一化探测场的正交振幅和相位算符,即

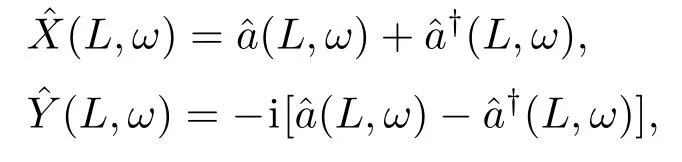
探测场的正交振幅和相位的关联噪声谱可定义为

在求解方程(17)的过程中,我们利用了关联函数,根据量子退化理论[33,34],即

其中N0=NV是介质的原子数,L表示光与原子相互作用的长度,表示µν的海森伯-郎之万运动方程中去掉郎之万噪声的动力学部分.

根据方程(18)以及系统的慢变海森伯-郎之万运动方程(2),我们可以得到郎之万噪声不为零的关联项,将其代入方程(17)后可获得振幅噪声谱(SX(L,ω))和相位噪声谱(SY(L,ω)),这里输出的探测场振幅噪声谱为

由于输出探测场相位噪声谱的计算过程和探测场振幅噪声谱的计算过程类似,同理可得

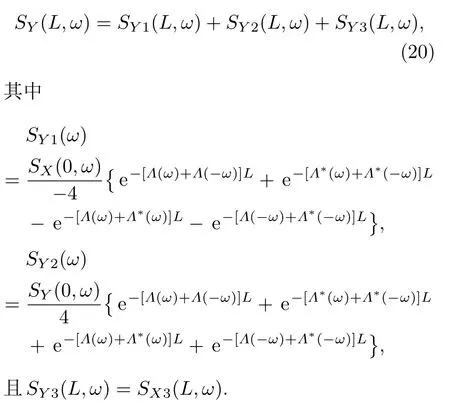
由方程(19)和方程(20)可知,探测场的输出振幅噪声和相位噪声主要有三个来源：其一,SX1(Y1)(L,ω)与探测场的输入振幅噪声SX(0,ω)有关;其二,SX2(Y2)(L,ω)与探测场的输入相位噪声SY(0,ω)有关,而且在介质中探测场的相位噪声可向其振幅噪声转化[35,36];其三,SX3(Y3)(L,ω)表示探测场的额外输出噪声,它与郎之万噪声有关,产生于原子随机衰减过程.

图4表示探测场振幅噪声谱、相位噪声谱以及探测光相位随双光子失谐的变化.当输入探测场是3 dB的振幅压缩场时(SX(0,ω)=0.5,SY(0,ω)=2),探测场输出噪声在宽的双光子失谐

图4 (网刊彩色)探测光相位为π时(红色实线)探测场振幅噪声谱(SX(s=L),蓝色短划线)和相位噪声谱(SY(s=L),绿色点划线)关于双光子失谐的函数变化Fig.4.(color online)Plot of amplitude-noise(SX(s=L),blue dashed-curve)and phase-noise(SY(s=L),green dot-dashed-curve)spectra versus two-photon detuning under the condition of a π-phase shift(red solid-curve).

δ2ph范围内几乎不变,此时额外量子噪声可忽略(参见绿色点划线和蓝色短划线),且相位移动保持为π(参见红色实线).因而,该系统可用来实现宽频域、低噪声、高保真量子相位门操控.

3 结 论

综上所述,我们提出利用一种新型三能级原子介质可实现低噪声弱光相位操控.这种相干制备的三能级原子介质具有一些有趣的性质,它能在一些特定模型中实现无损常数相位操控,无附加相位的吸收器/放大器,还有宽频域、高保真、低噪声相位门操控.同时锁定抽运光光强和双光子失谐时,探测光的吸收被显著抑制且能在宽频率范围内实现π相位.此外,利用该系统我们能够在探测光的光强为单光子/少光子的情况下,实现无损低噪声相位门操控或偏振门操控.上文中提到的模型系统在实验中是完全可行的,例如我们可以考虑一束连续的抽运光,它类似于EIT中的控制光只是相对于探测光为强光,拉比频率为Ω21/2π=30 MHz,另一束探测光为单光子脉冲光,脉冲宽度为10µs,单光子失谐为δ/2π=-1 GHz.在这样的系统参数下,抽运光的抽运率约为5.4×103s-1,在10µs的时间作用范围内,基态的粒子数的改变是微乎其微的,因此ρ11-ρ33的变化非常小.与此同时,探测光脉冲的工作区域是在吸收为零、增益也为零的区域,也就是说此时探测光没有任何增强和吸收,不影响基态粒子数布局.基于此系统的一系列特性,其在量子通信和量子计算领域具有极其重要的应用价值.

[1]Ottaviani C,Vitali D,Artoni M,Cataliotti F,Tombesi P 2003Phys.Rev.Lett.90 197902

[2]Fleischhauer M,Imamoğlu A,Marangos J P 2005Rev.Mod.Phys.77 633

[3]Harris S E,Field J E,Imamoğlu A 1990Phys.Rev.Lett.64 1107

[4]Hau L V,Harris S E,Dutton Z 1999Nature397 594

[5]Petrosyan D,Kurizki G 2002Phys.Rev.A65 033833

[6]Zhu C J,Deng L,Hagley E W 2014Phys.Rev.A90 063841

[7]Deng L,Payne M G 2007Phys.Rev.Lett.98 253902

[8]Jiang K J,Deng L,Payne M G 2006Phys.Rev.A74 041803

[9]Tan C H,Huang G X 2014Phys.Rev.A89 033860

[10]Huang G X,Hang C,Deng L 2008Phys.Rev.A77 011803

[11]Hang C,Huang G X 2010Opt.Express18 2952

[12]Zhu C J,Deng L,Hagley E W 2013Phys.Rev.A88 023854

[13]Li R B,Zhu C J,Deng L,Hagley E W 2014Appl.Phys.Lett.105 161103

[14]Bell W E,Bloom A L 1961Appl.Phys.Lett.6 280

[15]Alzetta G,Gozzini A,Moi L,Orriols G 1976Nuovo Cimento B36 5

[16]Alzetta G,Gozzini A,Moi L,Orriols G 1979Nuovo Cimento B52 209

[17]Arimondo E,Orriols G 1976Lett.Nuovo Cimento17 333

[18]Gray H R,Whitley R M,Stroud C R 1978Opt.Lett.3 218

[19]Arimondo E 1996Progress in Optics35 257

[20]Javan A 1957Phys.Rev.107 1579

[21]Hänsch T W,Toschek P E 1970Z.Phys.236 213

[22]Popova T Y,Popov A K,Rautian S G,Sokolovskii R I 1970Sov.Phys.JETP30 466

[23]Kocharovskaya O A,Khanin Y I 1988JETP Lett.48 630

[24]Harris S E 1989Phys.Rev.Lett.62 1033

[25]Schmidt H,Imamoğlu A 1996Opt.Lett.21 1936

[26]Lukin M D,Imamoğlu A 2000Phys.Rev.Lett.84 1419

[27]Fleishhauer M,Lukin M D 2000Phys.Rev.Lett.84 5094

[28]Deng L,Payne M G,Garrett W R 2004Opt.Commun.242 641

[29]Deng L,Payne M G,Hagley E W 2004Phys.Rev.A70 063813

[30]Deng L,Payne M G,Garrett W R 2006Phys.Rep.429 123

[31]Zhang J X,Cai J,Bai Y F,Gao J R,Zhu S Y 2007Phys.Rev.A76 033814

[32]Lu C P,Yuan C H,Zhang W P 2008Acta Phys.Sin.57 6976(in Chinese)[鲁翠萍,袁春华,张卫平 2008物理学报57 6976]

[33]Peng A,Johnsson M,Bowen W P,Lam P K,Bachor H A,Hope J J 2005Phys.Rev.A71 033809

[34]Chen Y C,Liao Y A,Chiu H Y,Su J J,Yu I A 2001Phys.Rev.A64 053806

[35]Polzik E S,Carri J,Kimble H J 1992Phys.Rev.Lett.68 3020

[36]Camparo J C 1998J.Opt.Soc.Am.B15 1177

PACS:42.50.-p,42.65.-k,42.50.Lc DOI:10.7498/aps.66.024205

Low-noise optical field phase-shifting manipulated using a coherently-prepared three-level atomic medium∗

Guan Jia Gu Yi-Sheng Zhu Cheng-Jie†Yang Ya-Ping‡

(School of Physics Science and Engineering,Tongji University,Shanghai 200092,China)

26 June 2016;revised manuscript

16 August 2016)

We propose a multifunction phase-shifting manipulator with low noise at a single-photon level,by using a threelevel atomic scheme.This three-level system interacts with a strong pumping field and a weak probe field with a large detuning.Due to this large detuning,two lower states can be coherently prepared prior to the injection of the pump and probe fields.In our configuration,the duration of the pumping field is much longer than that of the probe field.By solving the Heisenberg-Langevin equations of our system under the steady state approximation,we calculate the linear susceptibility of the system and examine the quantum noise properties of the probe field in detail.We show that this scheme,which rests on the process of two-wave mixing with initial atomic coherence,exhibits many interesting properties that neither typical electromagnetically induced transparency(EIT)schemes nor active Raman gain(ARG)schemes possess.Although both EIT-and ARG-based schemes have been widely investigated in atomic medium,the direct generalizations of these schemes to the single/few photon limit prove to be more problematic.The low fidelity due to the significant probe-field attenuation in EIT medium and the large quantum noise due to the amplification of the probe field in an active Raman gain medium are the main obstacles that prohibit a high-fidelity,low-noise phase shifter from being realized in the single/few photon limit.Physically,this scheme can be viewed as a hybrid scheme in which two processes of different physical principles are allowed to interfere with each other to achieve many desired functionalities.For instance,it can be used as a lossless two-photon-broadband phase-shifter with suitable system parameters.It can also be used as an attenuator/amplifier and a total transparency with a zero phase shift.In particular,we show that by locking the pump field intensity and the two-photon detuning simultaneously a flat constant π-phase shift can be realized with unit probe fidelity in a broad probe field frequency range.Applying the quantum regression theorem,we calculate the noise spectrum of the outgoing probe field as a large phase shift is achieved,and show that this two-photon-insensitive π-phase shift may significantly reduce the quantum noise fluctuations associated with a Raman gain process,and have a lot of potential applications for quantum information processing and optical telecommunication.The realization of this broadband π-phase-shift with significantly reduced quantum noise fluctuations makes this scheme attractive for the realization of low-noise phase-gate/polarization-gate at single-photon level.

nonlinear optics,coherent optical effects,quantum noise

:42.50.-p,42.65.-k,42.50.Lc

10.7498/aps.66.024205

∗国家重点基础研究发展计划(批准号：2016YFA0302800,2013CB632701)、国家自然科学基金(批准号：11504272,11474221)和上海科学技术委员会(批准号：15YF1412400)资助的课题．

†通信作者.E-mail：cjzhu@tongji.edu.cn

‡通信作者.E-mail：yang_yaping@tongji.edu.cn

*Project supported by the National Basic Research Program of China(Grant Nos.2016YFA0302800,2013CB632701),the National Natural Science Foundation of China(Grant Nos.11504272,11474221),and the Shanghai Science and Technology Committee,China(Grant No.15YF1412400).

†Corresponding author.E-mail：cjzhu@tongji.edu.cn

‡ Corresponding author.E-mail：yang_yaping@tongji.edu.cn