掺杂对称性对(110)晶向生长GaAs/AlGaAs量子阱中电子自旋弛豫动力学的影响∗

滕利华牟丽君

(青岛科技大学物理系,山东省新型光电材料与技术工程实验室,青岛 266061)

掺杂对称性对(110)晶向生长GaAs/AlGaAs量子阱中电子自旋弛豫动力学的影响∗

滕利华†牟丽君

(青岛科技大学物理系,山东省新型光电材料与技术工程实验室,青岛 266061)

(2016年1月1日收到;2016年10月10日收到修改稿)

采用时间分辨圆偏振光抽运-探测光谱,测量了(110)晶向生长的近似对称和完全非对称掺杂GaAs/AlGaAs量子阱中的电子自旋弛豫,发现两种量子阱材料中的电子自旋弛豫时间随载流子浓度的增大均呈现出先增大后减小的趋势,且近似对称掺杂GaAs量子阱中的电子自旋弛豫时间明显大于完全非对称掺杂量子阱.分析表明,在(110)晶向生长的GaAs量子阱中并非只有通常认为的Bir-Aronov-Pikus(BAP)机理起作用,在低载流子浓度区域,两种量子阱中D′yakonov-Perel′(DP)机理起主导作用,高载流子浓度区域BAP机理和DP机理都起作用,完全非对称掺杂的量子阱中DP机理强于近似对称掺杂量子阱.

圆偏振光饱和吸收光谱,电子自旋弛豫,掺杂对称性,GaAs/AlGaAs量子阱

1 引 言

利用电子自旋自由度取代或结合电荷自由度进行工作的自旋电子器件被认为在半导体纳米电子器件集成制造中具有广阔的应用前景[1,2].然而,这些应用都依赖于不同自旋弛豫寿命的获得,比如自旋光开关等自旋器件要求电子具有超快自旋弛豫过程,而量子信息存储器件等则要求自旋极化保持的时间足够长[3-5].半导体中电子自旋弛豫动力学及其随材料类型、材料结构以及环境等因素的变化研究一直是一个活跃的研究领域[3-8].

目前所研究的自旋电子学材料中,以量子阱材料为代表的异质结结构以其在自旋电子器件中的重要应用价值而备受关注.通常认为,在本征和n型掺杂的III-V族半导体量子阱中电子自旋弛豫的主要机理是DP机理[5,9,10].由结构的空间反演非对称所导致的Rashba效应和晶格的空间反演非对称所导致的Dresselhaus效应引起导带电子态的自旋劈裂,该效应等价于晶体内部存在一个有效磁场,从而引发和影响电子的自旋弛豫[10,11].在结构的空间反演对称GaAs量子阱中,Dresselhaus效应起主导作用.如果量子阱生长方向沿(001)或(111)晶向,有效磁场在量子阱平面内,可以引起垂直于量子阱平面方向的电子自旋弛豫;而对于(110)晶向生长的量子阱,有效磁场垂直于量子阱平面,因而Dresselhaus效应对垂直于量子阱平面方向的电子自旋弛豫没有贡献.再加上Rashba效应在结构空间反演对称GaAs量子阱中几乎不起作用,通常认为D′yakonov-Perel′(DP)机理在(110)晶向生长的量子阱中基本不起作用,因而,垂直于量子阱平面方向的电子自旋弛豫时间非常长[10].Ohno等[12]在低温下测得n型掺杂(110)晶向生长的GaAs量子阱中电子自旋弛豫时间在1 ns左右,掺杂浓度越低自旋弛豫时间越长,指出电子自旋弛豫的主要机理为电子-空穴散射引起的BAP机理;Eldrige等[13]测得常温下(110)晶向生长的本征GaAs量子阱中电子自旋弛豫时间超过1 ns;Völkl等[14]测得高迁移率(110)晶向生长的n型GaAs量子阱中电子自旋弛豫时间甚至可以超过16 ns,之前的研究结果普遍认为(110)晶向生长的GaAs量子阱中电子自旋弛豫的主要机理是Bir-Aronov-Pikus(BAP)机理[12,14].最近,Han等[15]分别测量了结构的空间反演对称和非对称(001)晶向生长n型掺杂GaAs量子阱中电子的自旋弛豫时间,发现由于非对称量子阱中存在较强的Rashba效应,由此产生的面内有效磁场会加速电子的自旋弛豫.对于(110)晶向生长的GaAs量子阱也应存在类似效应,那么结构的空间反演非对称(110)晶向生长的GaAs量子阱中电子自旋弛豫的机理是否仍然是BAP机理起主导作用?电子的自旋弛豫是否存在DP机理和BAP机理相互竞争的现象?深入研究(110)晶向生长的GaAs量子阱中电子初始自旋弛豫动力学,既是加深对半导体自旋电子学物理基础认识的需要,也是自旋电子器件发展的需要.为此,本文通过改变量子阱中n型掺杂位置的对称性而改变结构的空间反演对称性和势能结构的对称性,测量了掺杂位置近似对称和完全非对称(110)晶向生长的GaAs量子阱中的电子自旋弛豫时间,发现低载流子浓度区域DP机理起主导作用,高载流子浓度区域BAP机理和DP机理都起作用,完全非对称掺杂的量子阱中DP机理强于近似对称掺杂量子阱.

2 实验及结果

实验采用的样品如图1所示,样品A和B均由沿着(110)晶向生长的10个周期的GaAs/Al0.3Ga0.7As量子阱组成,每个势垒层均含有n型的Si调制掺杂层.其中,样品A除第1个量子阱以外,掺杂层的位置关于其余9个周期的量子阱对称,样品B中Si掺杂层的位置关于10个周期的量子阱都是非对称的,样品A和B中的掺杂电子浓度分别为2.5×1011cm-2和1.6×1011cm-2,具体的掺杂位置以及势阱层和势垒层的厚度如图1所示.

由自锁模钛宝石激光器输出的脉宽100 fs,中心波长850 nm,重复率82 MHz的激光脉冲列通过一个标准的抽运-探测装置[16,17],输出的抽运/探测光强比为5/1,在抽运光束中置一个1/2波片,分别控制抽运光束与探测光束为平行和正交线偏振,进而通过1/4波片分别产生同旋向和反旋向圆偏振抽运和探测光.抽运和探测光由一个焦距为50 mm的透镜聚焦于样品的同一点上,聚焦光斑的直径约为30µm.透过样品的圆偏振探测光的强度变化由光电管转换为电流,并由锁相放大器检测.一个连续可调衰减片用于控制输入光功率,达到改变激发载流子浓度的目的,实验中入射到样品的抽运光功率控制在1—18 mW之间.样品中的光激发载流子浓度N通过公式(1-R)Eα/(hνS)计算[5],其中R和α分别为反射比和吸收比,E为抽运光的单脉冲能量,hν为光子能量,S为抽运光斑面积.

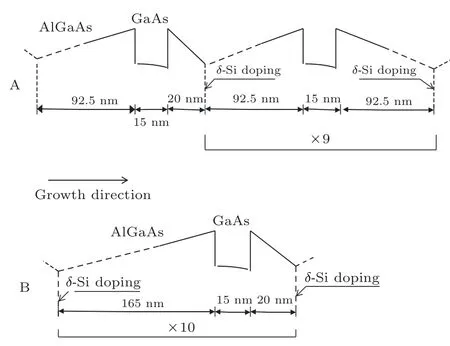
图1 量子阱A和B的势能图和掺杂位置Fig.1.Diagram of potential energy and doping position in quantum wells A and B.

在掺杂位置近似对称和完全非对称量子阱A和B中,分别测量了不同光激发载流子浓度N下圆偏振光抽运-探测的归一化饱和透射强度变化随延迟时间的扫描曲线.其中量子阱A和B中测得的两组典型曲线分别如图2(a)和图2(b)所示,红色实线(σ+,σ+)和黑色实线(σ+,σ-)分别表示同旋向和反旋向圆偏振光抽运-探测曲线.饱和透射强度变化可由如下模型描述[18,19]：

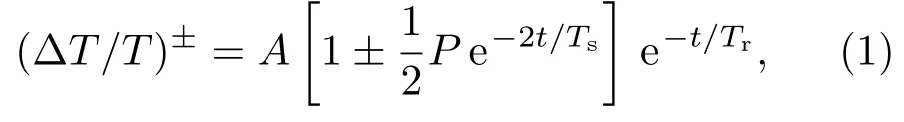
式中A为比例系数,P为电子初始自旋极化度,Ts和Tr分别为电子自旋弛豫时间和电子寿命,t为延迟时间,(ΔT/T)+和(ΔT/T)-分别表示同旋向和反旋向圆偏振光抽运-探测透射变化,绿色实线为利用饱和透射强度变化的理论模型拟合得到的曲线.实验结果显示,一定时间延迟后(σ+,σ+)和(σ+,σ-)趋于重合,自旋弛豫趋于结束.在量子阱A和B中,随载流子浓度的增大,(σ+,σ+)和(σ+,σ-)曲线的重合点都先向后移动,再向前移动,说明电子自旋弛豫时间随载流子浓度的增大呈现出先增大后减小的趋势.

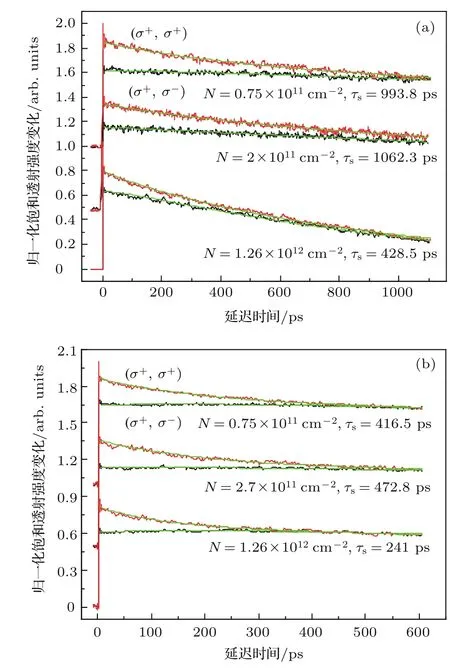
图2 (网刊彩色)掺杂位置近似对称(a)和完全非对称(b)量子阱中的归一化饱和透射强度变化 红色和黑色实线为同向和反向圆偏振光抽运-探测得到的饱和透射强度变化曲线,绿色实线为理论拟合曲线;除N=1.26×1012cm-2外,其他曲线的零基线均被漂移Fig.2.(color online)Normalized transmission changes in approximate symmetrical(a)and completely asymmetrical(b)doping quantum wells.The red and black solid lines are taken from co-helicity pump-probe beams and cross-helicity pump-probe beams,respectively.The green solid lines are the fittings with theoretical model.Differenty-axis offsets are added to each set of curves for clarity except the curves with carrier density of 1.26×1012cm-2.

3 自旋弛豫机理讨论

利用饱和透射强度变化的理论模型拟合实验曲线得到电子自旋弛豫时间随载流子浓度的关系如图3所示,红色圆点和黑色方形点分别为近似对称掺杂的量子阱A和完全非对称掺杂量子阱B中测得的自旋弛豫时间τsA和τsB.为了便于比较,我们同时测量了11个周期(001)晶向生长的本征GaAs/Al0.3Ga0.7As量子阱C的电子自旋弛豫时间τsC,如图3中绿色三角形点所示,该量子阱势阱和势垒层的厚度分别为10 nm和6 nm,结果显示在我们所测量的浓度范围内始终存在τsA＞τsB的关系.对于(001)晶向生长的本征GaAs量子阱C,DP机理是电子自旋弛豫的主要机理,BAP机理几乎不起作用,因而在非简并的低载流子浓度区,随载流子浓度的增大,动量散射增强,散射时间减小,电子自旋弛豫时间增大[9].与量子阱C相似,在载流子浓度分别低于2.1×1011cm-2和2.7×1011cm-2的范围内,在近似对称掺杂的量子阱A和完全非对称掺杂的量子阱B中,由于掺杂电子浓度分别为2.5×1011cm-2和1.6×1011cm-2,两种材料中均存在较强的电子-电子散射,随载流子浓度的增大,电子-电子散射增强,动量弛豫时间减小,电子自旋弛豫时间τsA和τsB均增大.由于BAP机理指出,电子自旋弛豫时间随载流子浓度的增大而减小[13,14,20],因此,在低浓度区量子阱A和B中的电子自旋弛豫的主导机理为DP机理.而在量子阱中DP机理是各向异性的,对于(001)晶向生长的量子阱C,由Dresselhaus自旋轨道耦合产生的有效磁场在量子阱平面内,垂直于量子阱平面方向的自旋极化将会感受到面内的随机磁场而进动,从而导致垂直于量子阱平面方向的自旋弛豫[10],但对于(110)晶向生长的量子阱,有效磁场垂直于量子阱平面,Dresselhaus效应对垂直于量子阱平面方向的电子自旋弛豫没有贡献,因而量子阱A和B是由Rashba自旋轨道耦合所产生的面内有效磁场导致了垂直于量子阱平面方向的自旋弛豫.

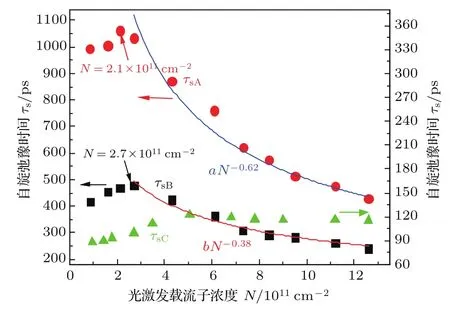
图3 (网刊彩色)量子阱A,B和C中电子自旋弛豫时间与载流子浓度的关系.Fig.3.(color online)Photocreated carrier density dependence of electron spin relaxation time in quantum wells A,B and C.

掺杂近似对称和完全非对称的量子阱A和B中,分别具有近似对称的势能结构和完全非对称的势能结构.非对称的势能结构会引起强的内建电场,从而导致由Rashba自旋轨道耦合所产生的面内有效磁场,该有效磁场能对垂直于量子阱平面方向的自旋极化产生作用,使其进行Larmor进动,导致自旋弛豫.因此,量子阱中势能结构的非对称性引起的Rashba自旋轨道耦合导致τsB明显小于τsA.我们的实验结果表明,通过改变掺杂位置的对称性改变量子阱的势能结构,可以有效地改变(110)GaAs量子阱的自旋弛豫速率.因此,在低浓度区量子阱A和B中的电子自旋弛豫机理为DP机理,且非对称性越强,Rashba效应越强,DP机理越明显,自旋弛豫时间越短;反之,自旋弛豫时间越长.

当载流子浓度分别高于2.1×1011cm-2和2.7×1011cm-2时,在量子阱A和B中,电子自旋弛豫时间均随载流子浓度的增大而迅速减小,此时载流子浓度远高于两种材料中的掺杂电子浓度,电子-空穴交换相互作用随载流子浓度的增大迅速增强,正如之前所报导的,BAP机理开始起重要作用[12,14].然而,此时DP机理是否仍起作用?如图3中蓝色和红色实线所示,我们拟合发现量子阱A和B中测得的电子自旋弛豫时间与载流子浓度之间分别服从τs=aN-0.62和τs=bN-0.38的关系,而BAP机理指出电子自旋弛豫时间τs与N-1之间成正比[13],显然我们测得的量子阱A和B中的电子自旋弛豫时间随载流子浓度的衰减速率均小于只有BAP机理作用的情况,原因是DP机理在该浓度区也起作用.正如量子阱C中的测量结果显示,在载流子浓度较高的简并区,电子自旋弛豫的主要机理仍为DP机理,且由于非均匀扩展对电子自旋弛豫的加速作用,致使电子自旋弛豫时间不再增大甚至有略微减小的趋势[5],但DP机理作用下的电子自旋弛豫时间随载流子浓度的衰减速率远小于BAP机理,所以在DP机理也起作用的情况下,量子阱A和B中的电子自旋弛豫时间随载流子浓度的衰减速率均小于只有BAP机理作用的情况.

正是由于DP机理在量子阱A和B的高浓度区也起作用,完全非对称掺杂的量子阱B中Rashba效应强于近似对称掺杂的量子阱A,DP机理更强,而两种材料中BAP机理强度差别不大,因此,τsB明显小于τsA.另外,自旋弛豫时间随载流子浓度的衰减速率取决于BAP机理和DP机理的相对强度,完全非对称量子阱B中电子自旋弛豫时间随载流子浓度的衰减比量子阱A更慢,原因同样在于该量子阱中DP机理的作用强于量子阱A.

4 结 论

通过测量掺杂近似对称和完全非对称GaAs/AlGaAs量子阱中电子自旋弛豫时间的载流子浓度依赖关系,发现在(110)晶向生长的GaAs量子阱中并非只有BAP机理起作用,在低载流子浓度区域,两种量子阱材料中DP机理起主导作用,高载流子浓度区域BAP机理和DP机理都起作用.掺杂位置的不对称导致势能结构的不对称,从而引起内建电场的产生,进而引起由Rashba自旋轨道耦合所产生的面内有效磁场,最终引起垂直于量子阱平面方向的电子自旋弛豫,因而完全非对称掺杂的量子阱中DP机理强于近似对称掺杂量子阱,而两种材料中BAP机理强度差别不大,因此在整个浓度范围内完全非对称掺杂的量子阱中的电子自旋弛豫时间都小于近似对称掺杂量子阱.

[1]Zutic I,Fabian J,Das Sarma S 2004Rev.Mod.Phys.76 323

[2]Loss D,DiVincenzo D P 1998Phys.Rev.A57 120

[3]Zhang T T,Barate P,Nguyen C T,Balocchi A,Amand T,Renucci P,Carrere H,Urbaszek B,Marie X 2013Phys.Rev.B87 041201

[4]Krishnamurthy S,van Schilfgaarde M,Newman N 2003Appl.Phys.Lett.83 1761

[5]Teng L H,Zhang P,Lai T S,Wu M W 2008Europhys.Lett.84 27006

[6]Lai T S,Teng L H,Jiao Z X,Xu H H,Lei L,Wen J H,Lin W Z 2007Appl.Phys.Lett.91 062110

[7]Lai T S,Liu X D,Xu H H,Jiao Z X,Wen J H,Lin W Z 2006Appl.Phys.Lett.88 192106

[8]Chen X X,Teng L H,Liu X D,Huang Q W,Wen J H,Lin W Z,Lai T S 2008Acta Phys.Sin.57 3853(in Chinese)[陈小雪,滕利华,刘晓东,黄绮雯,文锦辉,林位株,赖天树2008物理学报57 3853]

[9]Wu Y,Jiao Z X,Lei L,Wen J H,Lai T S,Lin W Z 2006Acta Phys.Sin.55 2961(in Chinese)[吴羽,焦中兴,雷亮,文锦辉,赖天树,林位株2006物理学报55 2961]

[10]Wu M W,Jiang J H,Weng M Q 2010Phys.Reports493 61

[11]Xia J B,Ge W K,Chang K 2008Semiconductor Spintronics(Beijing：Science Press)p216(in Chinese)[夏建白,葛惟昆,常凯 2008半导体自旋电子学 (北京：科学出版社)第216页]

[12]Ohno Y,Terauchi R,Adachi T,Matsukura F,Ohno H 1999Phys.Rev.Lett.83 4196

[13]Eldridge P S,Lagoudakis P G,Henini M,Harley R T 2010Phys.Rev.B81 033302

[14]Völkl R,Griesbeck M,Tarasenko S A,Schuh D,Wegscheider W,Schüller C,Korn T 2011Phys.Rev.B83 241306

[15]Han L F,Zhu Y G,Zhang X H,Tian P H,Ni H Q,Niu Z C 2011Nanoscale Res.Lett.6 84

[16]Xu H H,Jiao Z X,Liu X D,Lei L,Wen J H,Wang H,Lin W Z,Lai T S 2006Acta Phys.Sin.55 2618(in Chinese)[徐海红,焦中兴,刘晓东,雷亮,文锦辉,王惠,林位株,赖天树2006物理学报55 2618]

[17]Teng L H,Mu L J,Wang X 2014Physica B436 177

[18]Lai T S,Liu L N,Shou Q,Lei L,Lin W Z 2004Appl.Phys.Lett.85 4040

[19]Teng L H,Chen K,Wen J H,Lin W Z,Lai T S 2009J.Phys.D:Appl.Phys.42 135111

[20]Völkl R,Schwemmer M,Griesbeck M,Tarasenko S A,Schuh D,Wegscheider W,Schüller C,Korn T 2014Phys.Rev.B89 075424

GaAs/AlGaAs quantum wells

PACS:68.65.Fg,72.25.Fe,72.25.Rb DOI:10.7498/aps.66.046802

Effect of doping symmetry on electron spin relaxation dynamics in(110)GaAs/AlGaAs quantum wells∗

Teng Li-Hua†Mu Li-Jun
(Optoelectronic Materials and Technologies Engineering Laboratory of Shandong,Department of Physics,Qingdao University of Science and Technology,Qingdao 266061,China)

1 January 2016;revised manuscript

10 October 2016)

Considerable interest has been aroused in the study of the spin dynamics in semiconductors due to its potential applications in spintronics and quantum computation.In this paper,time-resolved circularly polarized pump-probe spectroscopy is used to study the carrier density dependences on the electron spin relaxation in approximately symmetrical and completely asymmetrical doping(110)GaAs/AlGaAs quantum wells.With the increase of the carrier density,the spin relaxation time first increases and then decrease obviously in both of the quantum wells,and the measured spin relaxation time of the approximately symmetrical doping quantum wells is always longer than that of the asymmetrical doping one.By analysis,we find that the spin relaxation is not dominated only by the Bir-Aronov-Pikus(BAP)mechanism in(110)GaAs quantum wells,that though the Dresselhaus spin-orbit coupling does not lead to any spin relaxation,the asymmetry of the doping position contributes to the asymmetry of potential energy structure,thus the built-in electric field which can induce the Rashba spin-orbit coupling to appear,and that the effective magneticfield induced by the Rashba spin-orbit coupling normal to the growth direction can lead to spin relaxation along the growth direction.Therefore,the D′yakonov-Perel′(DP)mechanism plays an important role in asymmetrical doping(110)GaAs/AlGaAs quantum wells.In the approximately symmetrical and completely asymmetrical doping(110)GaAs/AlGaAs quantum wells,the DP mechanism dominates the spin relaxation at low carrier density,thus the spin relaxation time increases with carrier density increasing due to the strengthening of the electron-electron scattering and the decreasing of the momentum relaxation time.However,at high carrier density,BAP mechanism plays an important role,thus the spin relaxation time decreases obviously with carrier density increrasing,but the decay rates in both of the quantum wells are slower than that in the casethat only BAP mechanism dominates,because both the DP and BAP mechanism play an important role.The strength of the Rashba spin-orbit coupling depends on the symmetry of the quantum well.The DP mechanism in a completely asymmetrical doping quantum well is stronger than that in an approximately symmetrical doping quantum wells,thus the decay rate in a completely asymmetrical doping quantum wells is always slower than that in an approximately symmetrical doping quantum wells,and the spin relaxation time in a completely asymmetrical doping quantum wells is shorter than that in an approximately symmetrical doping quantum wells.

circularly polarized pump-probe spectroscopy,electron spin relaxation,doping symmetry,

:68.65.Fg,72.25.Fe,72.25.Rb

10.7498/aps.66.046802

∗国家自然科学基金(批准号：11504194,11274189)和青岛市应用基础研究计划项目青年专项(批准号：14-2-4-101-jch)资助的课题.

†通信作者.E-mail：tenglihua80@163.com

*Project supported by the National Natural Science Foundation of China(Grant Nos.11504194,11274189)and the Scientific Development Project of Qingdao,China(Grant No.14-2-4-101-jch).

†Corresponding author.E-mail：tenglihua80@163.com