攻角对火星降落伞拉直过程的影响分析
鲁媛媛 荣伟 吴世通
(北京空间机电研究所,北京 100094)
攻角对火星降落伞拉直过程的影响分析
鲁媛媛 荣伟 吴世通
(北京空间机电研究所,北京 100094)
为了研究火星探测器减速着陆系统降落伞开伞前进入舱攻角的大小对伞拉直过程的影响,设计相应的控制措施,文章以“海盗号”火星探测器为研究对象,建立了基于质量阻尼弹簧模型的降落伞拉直过程动力学模型,研究了进入舱不同攻角下降落伞的拉直过程,重点研究了攻角与“绳帆”现象之间的关系。结果表明,火星环境下开伞前进入舱攻角越大,拉直过程中的“绳帆”现象越严重。因此,减小开伞前进入舱的攻角,将有利于避免或降低“绳帆”现象的发生。这一研究结论可为火星探测减速着陆系统的设计提供一定参考。
火星探测器 降落伞拉直过程 绳帆 攻角 “海盗号”
0 引言
降落伞拉直是开伞过程的第一个动作,是指从开始弹(拉)伞到伞全部拉直的整个过程。作用在伞绳和未充气伞衣上的气动力对降落伞能否正常充气以及伞衣结构完整性有着重要的影响。降落伞系统设计的期望是拉直方向与相对气流方向平行,但是当拉直方向与相对气流方向具有一定夹角时,会导致伞绳偏离拉直方向,使伞绳过早拉出,伞绳发生弯曲,这就是“绳帆”现象[1]。“绳帆”现象可能会导致改变拉直时间、过度增加拉直力、非对称拉直、伞衣损坏,以及非对称充气、充气时发生漏气塌陷等一系列不可预测的现象[2]。
美国航空航天局(NASA)非常重视火星探测器开伞前进入舱的攻角(以下简称开伞攻角)大小。NASA的设计人员提出,攻角是一个关键参数,它影响降落伞正常拉直和充气、着陆器的轴向过载,以及开伞后舱伞系统的动力学特性[3-4]。根据“海盗号”的飞行数据,进入舱攻角必须满足不大于13°,才能保证降落伞正常充气[5];NASA的最新一代火星探测器“火星科学实验室”在降落伞开伞前15s,通过依次分离进入舱内部的6个质量块(如图1),改变进入舱质心位置,使开伞前进入舱的配平攻角降至0°左右(如图2)[6]。而在地球环境下,返回式卫星或载人飞船对开伞攻角大小并没有特别的要求。载人飞船返回舱的伞舱一般安装在舱体侧面,进行侧向开伞,这种安装结构本身就使开伞时返回舱具有较大的攻角。
因此在火星环境下,开伞攻角的大小可能对降落伞的拉直过程存在一定影响。针对这一问题,截至目前,在国内公开发表的论文中未见相关研究。在进行火星探测器减速着陆系统设计时,必须搞清楚开伞攻角对火星探测器降落伞拉直过程动力学特性的影响。本文针对这一问题进行深入研究和分析,重点研究开伞攻角与“绳帆”现象之间的关系。
1 动力学建模
火星探测器降落伞拉直过程中舱伞系统包括伞包、伞绳/伞衣、进入舱等三部分,模型中将伞包视为变质量刚体,将进入舱视为刚体。伞绳/伞衣采用质量阻尼弹簧模型,即将伞衣/伞绳离散成若干绳段,每个绳段处理为质量集中在两端的质点,各质点之间以阻尼弹簧相连(如图 3)。拉直过程中,伞衣和伞绳分为未拉出部分(包裹在伞包中,随伞包一起运动)、正在拉出的部分和已拉出部分。拉直过程中伞绳/伞衣的质点分布如图4所示。
以下分别对伞包、进入舱,以及拉直过程中伞绳/伞衣的动力学模型进行简要描述。
(1)伞包和进入舱刚体运动方程
伞包和进入舱运动方程均采用刚体动力学基本方程,矢量表达式为:
式中 m为刚体质量;t为运动时间;V为刚体质心速度矢量;F为作用在刚体上的合力;H为刚体相对于质心的动量矩;M为作用在刚体上的合力矩。
(2)伞绳/伞衣绳段节点的运动方程
已拉出绳段节点的受力包括重力、相邻绳段的拉力以及气动力。设已拉出绳段节点数为 N,则已拉出绳段节点 i( 1,2 ,3,…, N)的运动方程为:
式中 mi为已拉出节点i的质量;Vi、si分别为节点i的速度和位移;Qi、Ti、Gi分别为节点i所受气动力、相邻绳段张力、重力。
正在拉出绳段节点的运动方程根据动量定理推导得出,对正在拉出微元质量 dmi的绳段,其动量方程为
式中 ui为绳段的拉出速度;Ti为正在拉出绳段的张力;Fi为绳段拉出阻力,包括摩擦力和捆绑绳约束力。
将式(3)中各向量向绳段体坐标系投影,可推导出
式中im′为正在拉出绳段的线密度。
当正在拉出绳段达到其原长时,认为绳段完全从伞包中拉出,已拉直绳段数目增加1个。详细的降落伞拉直过程数学模型可见文献[7]。
2 降落伞拉直过程动力学特性分析
1972 年NASA进行了“海盗号”第一次气球发射试验(Balloon Launched Decelerator Test,BLDT AV-1),试验中降落伞开伞时飞行器的攻角为13°,降落伞在拉直过程中出现了明显的“绳帆”现象,导致降落伞非对称充气,并最终导致了伞衣在充气过程中出现部分破损[8]。本文利用此试验的相关数据[9-13],以“海盗号”为研究对象,分别从舱伞系统位形图、伞绳/伞衣的最大偏离距离、张力、拉出速度几方面研究了开伞攻角为0°、5°、10°、15°、20°、25°、30°时降落伞拉直过程的动力学特性。
2.1 舱伞系统位形图
不同攻角对应的拉直过程中舱伞系统在水平方向和垂直方向的空间位形如图5所示。图5(a)为攻角0°时的舱伞系统位形图,伞绳在拉直过程中呈一条直线,最大偏离距离仅为0.01m;图5(b)是攻角为10°时的舱伞系统位形图,最大偏离距离为1.17m;图5(c)~(d)分别对应开伞攻角为20°、30°时的拉直过程,可以看出,随着攻角增大,“绳帆”现象越来越明显,当攻角为 30°时,最大偏离距离达到了5.56m,对于长度为27.43m的伞绳来说,弯曲程度非常严重。
2.2 最大偏离距离
为了定量研究“绳帆”现象的严重程度,文中采用了最大偏离距离这一指标衡量拉直过程中伞绳/伞衣的弯曲程度[14]。如图6所示,理想的拉直过程是拉直方向始终与伞包和进入舱呈一条直线,即拉出的伞绳/伞衣始终与直线BP重合,其中点B是伞绳脱离伞包的位置,点P是伞绳与进入舱的连接点,所有拉出的伞绳/伞衣节点与直线BP之间的最大垂直距离即为此时刻的伞绳最大偏离距离。
图7是不同攻角对应的伞绳最大偏离距离随拉直时间的变化曲线。从图中可以看出,最大偏离距离先逐渐增加,到某一时刻后急剧下降,然后再缓慢上升。各曲线的峰值对应拉动伞衣底边的时刻,当拉动伞衣底边时,伞绳突然绷紧,伞绳张力增大,导致伞绳偏离距离随后突然减小。伞衣底边拉出后,伞绳张力变小,伞绳偏离距离又逐渐增大。
根据以上分析,开伞攻角越大,降落伞拉直过程中伞绳的最大偏离距离越大,“绳帆”现象越严重。这是由于当开伞存在一定的攻角时,降落伞的拉直方向与气流方向存在一定夹角,从而形成侧向干扰气流,使伞绳/伞衣偏离拉直方向,从而产生“绳帆”现象。攻角越大,伞绳/伞衣受到的气动力在垂直于理想拉直方向上的分量大,即侧向气动力越大,空间位形越弯曲。
2.3 伞绳张力
拉直过程中不同攻角对应的伞绳张力随拉直时间的变化曲线如图8所示。从伞绳张力的变化趋势中可以看出,伞绳张力在开始拉伞的0.1s内变化非常剧烈,由0N迅速增大至2 000~4 000N,然后又下降至 500N左右,这是由于弹伞筒点火,以一定的速度弹出伞包,伞包与进入舱的速度差使伞绳迅速绷紧并开始拉伞。此后伞绳张力变化平缓,到某一时刻后急剧上升至峰值(即拉直力) ,然后又迅速下降,这是由于拉动伞衣底边时,绳段质量突然增大,根据动量定理,在伞绳中会出现一个拉直载荷的跃升,可见拉直力出现在伞衣底边拉动的瞬间。
此外,观察图8还可以发现,不同攻角对伞绳张力以及拉直力大小的影响不大。攻角越大,拉直力出现的时间越早,即拉动伞衣底边的时间越早,因此拉直时间越短。
2.4 拉出速度
不同攻角对应拉出速度随拉直时间的变化如图9所示。从图中可看出,弹伞初始时刻,拉出速度迅速上升至32m/s左右,约1s时,伞衣底边被拉动,拉出速度突然减小,这是由于伞衣底边对应的绳段节点质量突然变大,伞包动量减小所导致。约1s之后的伞衣拉出阶段,拉出速度急剧下降,然后又上升再下降,这分别对应于火星盘缝带伞的“带”、“缝”和“盘”的拉出阶段[16]。拉出“带”和“盘”时,由于拉出质量大,拉出阻力也大,从而导致拉出速度小。拉出“缝”时,拉出质量和阻力都小,因此拉出速度大。约1.2s之后拉出速度迅速减小,这是由于拉直过程中伞包速度逐渐减小,与相邻正在拉出节点的速度差越来越小,导致拉出速度越来越小。
此外,观察图9还可以发现,当攻角为0°~10°时,伞衣底边拉动之前的拉出速度一直呈减小趋势;而当攻角为 15°~30°时,此段拉出速度先减小后增大,且攻角越大,这种变化趋势愈明显。因为开伞攻角越大,降落伞在拉直过程中越易受到侧向气流的影响,侧向气流使伞绳相邻节点的速度差变大,从而导致拉出速度增大。这在一定程度上也反映了拉直过程中的“绳帆”现象。因此,开伞前进入舱攻角越大,伞绳拉出速度越大,拉直时间越短。
2.5 主要特征值分析
不同攻角对应的拉直过程中的主要特征值如表1所示。可以看出:开伞前进入舱攻角越大,拉直过程中的伞绳最大偏离距离越大;攻角从0°增大至30°,最大偏离距离从0.01m增大至5.56m;攻角越大,拉直时间越短,因此较大的攻角会使伞绳过早拉出,导致降落伞拉出时间发生很大变化,从而不能准确预测降落伞的充气过程;拉直力与攻角成正比,当攻角较小时(<10°),攻角对拉直力的影响较小,当攻角>10°时,攻角越大,拉直力越大。
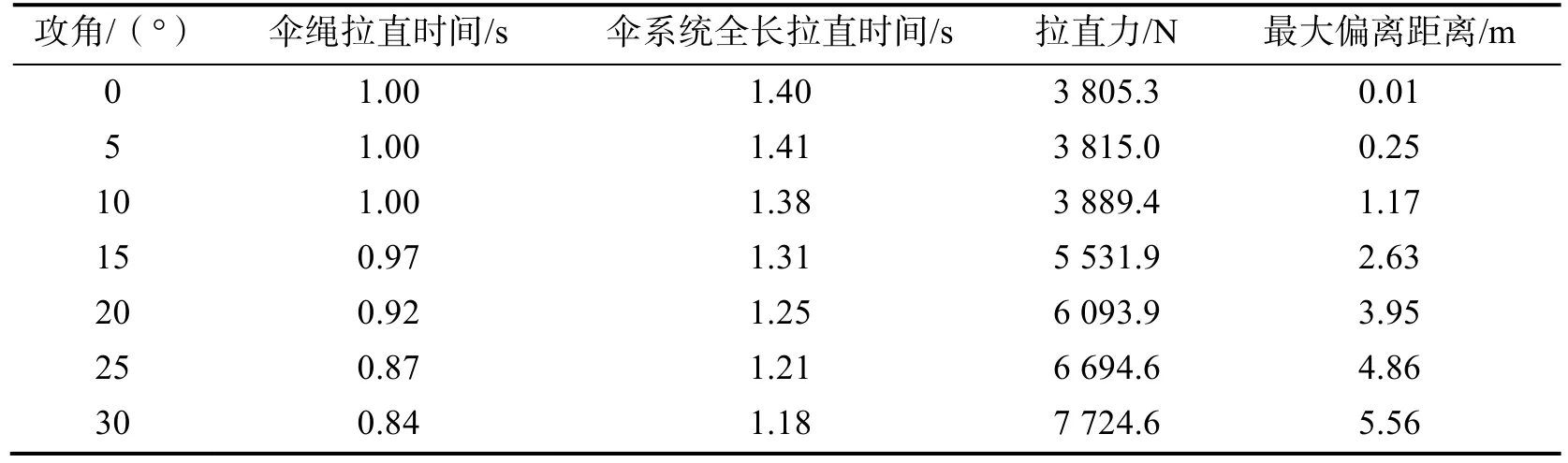
表1 拉直过程仿真结果Tab.1 Simulation results of parachute deployment
3 结论
本文利用“海盗号”第一次气球发射试验的相关数据,以“海盗号”为研究对象,研究了在模拟火星环境下,开伞攻角对降落伞拉直过程动力学特性的影响。通过对不同攻角对应的拉直过程中舱伞系统位形图、最大偏离距离、伞绳张力、拉出速度及主要特征值进行对比,可得出如下结论:1)开伞攻角越大,“绳帆”现象越严重;2)开伞攻角越大,拉直时间越短,从而导致不能准确预测降落伞的拉出时间和充气过程;3)当开伞攻角较小时(<10°),攻角对拉直力的影响较小;当攻角>10°时,攻角越大,拉直力越大。所以,为了减小或消除“绳帆”现象,应尽量减小火星探测器开伞前进入舱的攻角。
References)
[1]王海涛, 秦子增, 宋旭民, 等. 大型降落伞拉直过程中的抽打现象分析[J]. 国防科学技术大学学报, 2010, 32(5): 34-38. WANG Haitao, QIN Zizeng, SONG Xumin, et al. Analysis of the Phenomenon of Bull Whipping in the Deployment Process of Large Parchute[J]. Journal of National University of Defense Technology, 2010, 32(5): 34-38. (in Chinese)
[2]夏刚, 秦子增, 张晓今, 等. “绳帆” 现象及其对开伞过程的影响[J]. 航天返回与遥感, 2001, 22(4): 1-5. XIA Gang, QIN Zizeng, ZHANG Xiaojin, et al. Line Sail and Its Influences on Deployment Performance of Parachute System[J]. Spacecraft Recovery & Remote Sensing, 2001, 22(4): 1-5. (in Chinese)
[3]GROVER R. Overview of the Phoenix Entry, Descent and Landing System[R]. Ames Research Center Jet Propulsion Laboratory, 2005.
[4]GROVER M R, CICHY B D, DESAI P N. Overview of the Phoenix Entry, Descent and Landing System Architecture[R]. AIAA 2008-7218, 2008.
[5]KIPP D, MARTIN M S, ESSMILLER J, et al. Mars Science Laboratory Entry, Descent, and Landing Triggers[C]. IEEE Aerospace Conference, 2007.
[6]MCVEY D F, WOLF D F. Analysis of Deployment and Inflation of Large Ribbon Parachutes[C]. AIAA AerodynamicDeceleration Systems Conference, 4th, 1973.
[7]鲁媛媛, 荣伟, 吴世通. 火星环境下降落伞拉直过程的动力学建模[J]. 航天返回与遥感, 2014(1): 29-36. LU Yuanyuan, RONG Wei, WU Shitong. Dynamic Modeling of Parachute Deployment in Mars Environment[J]. Spacecraft Recovery & Remote Sensing, 2014(1): 29-36. (in Chinese)
[8]DICKINSON D, SCHLEMMER J, HICKS F, et al. Balloon Launched Decelerator Test Program Post-flight Test Report BLDT Vehicle AV-1[R]. NASA-CR-112176, 1972.
[9]MOOGR D, MICHEL F C. Balloon Launched Viking Decelerator Test Program[R]. NASA-CR-112288, 1973.
[10]LAU R A, HUSSONG J C. The Viking Mars Lander Decelerator System[C]. AIAA Aerodynamic Deceleration Systems Conference, 1970.
[11]SOFFEN G A. Mars and the Remarkable Viking Results[C]. AIAA Aerospace Sciences Meeting, 16th, 1978.
[12]CORLISS W R. The Viking Mission to Mars[R]. NASA SP-334, 1974.
[13]QUINN J M. Viking Data Analysis[R]. ADA222609, 1995.
[14]张青斌, 彭勇, 程文科, 等. 降落伞拉直过程的质量阻尼弹簧模型[J]. 弹道学报, 2003, 15(1): 31-36. ZHANG Qinbin, PENG Yong, CHENG Wenke, et al. A Mass Spring Damper Model of Parachute Deployment[J]. Journal of Ballistics, 2003, 15(1): 31-36. (in Chinese)
[15]王立荣. 降落伞理论与应用[M]. 北京: 宇航出版社, 1997. WANG Lirong. Parachute Theory and Application[M]. Beijing: China Astronautic Publishing House, 1997. (in Chinese)
[16]GILLIS C. The Viking Decelerator System An Overview[C]. AIAA Aerodynamic Deceleration Systems Conference, 4th, 1973.
Impact Analysis of Attack Angle on Dynamics Characteristic of Mars Probe Parachute Deployment
LU Yuanyuan RONG Wei WU Shitong
(Beijing Institute of Space Mechanics & Electricity, Beijing 100094, China)
In order to research the influence of attack angle of vehicle on parachute deployment process on Mars, this paper studies the influence of attack angle of vehicle on dynamics of parachute deployment process on Mars by taking Viking as research object. The relationship of attack angle and line sail is studied. The results show that the larger the attack angle is, the more serious line sail during the parachute deployment will be. To avoid or ease the line sail, it’s necessary to reduce the angle of attack of vehicle. The study provides a reference for descent and landing system design of Mars probe for China.
Mars probe; parachute deployment; line sail; angle of attack; Viking
V529.1
A
1009-8518(2017)03-0024-07
10.3969/j.issn.1009-8518.2017.03.003
鲁媛媛,女,1983年生,2015年获中国空间技术研究院飞行器设计专业博士学位,工程师。研究方向为航天器返回与着陆技术。E-mail:quaner527@aliyun.com。
(编辑:夏淑密)
2017-01-09

