因式分解的方法与技巧

文/惠州市惠阳区新圩中学 严华春

因式分解的方法与技巧

文/惠州市惠阳区新圩中学 严华春

分解因式的数学思想分为类比思想和归化思想，类比思想是指运用整式的乘法进行分解因式的探索活动，体现整式乘法与分解因式之间的互逆关系。而归化思想是指将求解方程化为f（x）=0，对f（x）进行因式分解，然后令各个因式为0，从而求得原方程的解的思想。运用类比思想和额归化思想，较常见的因式分解方法有以下几种。

1.提公因式法

如果一个多项式的各项都含有公因式，那么就可以把这个公因式提出来，从而将多项式化成两个因式相乘的形式。提公因式法比较适用于一些各部分都有公共因式的题目，其可以比较快速的将题目化简，从而进一步的观察和尝试。

例：分解因式5x3+10x2+5x

方法与技巧：显然，每项均含有公因式5x，故可考虑提取公因式5x，接下来只剩下x2+2x+1，但仍可继续分解；在这个多项式中，虽然可以用其它方法，但分解起来都很麻烦，只要提取一个公因式就得到一个可用完全平方和的式子，从而简单的就解答出来了。

解：原式=5x（x2+2x+1）=5x（x+ 1）2

2.公式法

多项式如果满足特殊公式的结构特征时即可采用公式法进行多项式的因式分解，故对于一些常用的公式要求熟记，除教材的公式外，数学竞赛中常出现一些基本公式，归纳整理如下：平方差公式：a2-b2=（a+b）（a-b）；完全平方和公式：a2+2ab+b2=（a+b）2；完全平方差公式：a2-2ab+b2=（a-b）2；立方和公式：a3+b3=（a+b）（a2-ab+b2）；立方差公式：a3-b3=（a-b）（a2+ab+b2）。

3.分组分解法

根据多项式的特点将其适当的分组，然后各组分别变形。例如把多项式am+an+bm+bn分解因式，可以先把前两项分成一组，并提出公因式a，把它后两项分成一组，并提出公因式b，从而得到a(m+n) +b(m+n)，又可以提出公因式，从而得到 (a+b)(m+n)。

4.十字相乘法

在解决二次多项式时，十字相乘法是常用的基本方法，对于mx2+px+q形式的多项式，如果a× b=m，c×d=q且ac+bd=p，则多项式可因式分解为 (ax+d)(bx+c)，为方便起见，我们将上形要求用下图显示。

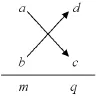
例：分解因式7x2-19x-6方法与技巧：

1×7=7，-3×2=-6，1×2+（-3）× 7=-19

解：原式=（x-3）（7x-2）

5.配方法

对于那些不能利用公式的多项式，有部分可以利用配方法将其配成一个完全平方式，然后再利用完全平方公式，将其因式分解，以便进一步观察。

例：分解因式x2+6x-7

方法与技巧：把-7分成9-16就可以分配成（x2+6x+9）-16，而前三项是一个完全平方和，16是4的平方，又可以和前三项构成平方差，因此式子可以这样解：

原式=（x2+6x+9）-16

=（x+3）2-42

=（x+7）（x-1）

6.拆、添项法

把多项式的某一项拆开或填补上互为相反数的两项 （或几项），使原式适合于提公因式法，运用公式或分组分解进行分解。要注意，必须在与原多项式相等的原则下进行变形。

例：分解因式x5+x+1

方法与技巧：在x+1中，增加一个x2才能形成一个完全平方和，因此原式中加一个x2，同时要减去一个x2才能使原式不变，因此有以下的解：

原式=（x5-x2）（x2+x+1）

=x2（x3-1）（x2+x+1）

=x2（x-1）（x2+x+1）（x2+x+ 1）

=（x2+x+1）（x3-x2+1）

7.换元法

在某些多项式的因式分解的过程中，通过换元，可以把形式复杂的多项式变为形式简单、易于分解的多项式，从而使问题化繁为简，迅速的解答出来。

例：分解因式 （x2+7x-5）（x2+ 7x+3）-33

方法与技巧：在这式子里，如果先分解因式将会使式子变得更复杂，我们可以发现x2+7x-5和x2+ 7x+3都含有 x2+7x，因此设 y=x2+ 7x。这种方法可以使式子的形式比较简单，使我们在做题时不易出差错，但要在式子所有多项式都含有相同部分才能如此换元。

8.赋值法

取包含在问题的条件 (或结论)中的某个特殊值，或某个特殊情形，经过简单的推理、判断或运算，就能得出问题的正确答案，由于分解因式是恒等变形，一个多项式分解后字母取任意值，它都应该是成立的。因而可取某字母为“0”、 “1”等特殊值，把原式消元转化后再来分解。

例：x2+2xy+y2+2x+2y-3

方法与技巧：直观上不能比较快的观察出有公因式或者可以直接运用公式法，但我们可以先设x2+ 2xy+y2+2x+2y-3=(a1x+b1y+c1)(a2x+ b2y+c2)， 然后令 y=0求出 a1、a2、c1、c2，再令x=0，可求出 b1、b2，最后把所有未知数代入原来所设的式子，就可以简单的求解出来。

解：原式=(a1x+b1y+c1)(a2x+ b2y+c2)

令y＝0，则原式=x2＋2x－3

=（x＋3）（x－1）

=（a1x＋c1）（a2x＋c2）

所以，a1=a2=1，c1=3，c2=-1。

令x=0，同理可以求出b1=1，b2=1。

整理得：原式=（x+y+3）(x+y-1)。

责任编辑 黄日暖

见习编辑 黄博彦