超声污水流量测量的数学建模及影响因素分析

任增强，李跃忠∗，钱永安

(1.东华理工大学机械与电子工程学院,江西南昌330013；2.江西省新能源工艺及装备工程技术研究中心（东华理工大学），江西南昌330013；3.江西省计量测试研究院,江西南昌330002)

超声污水流量测量的数学建模及影响因素分析

任增强1,2，李跃忠1,2∗，钱永安3

(1.东华理工大学机械与电子工程学院,江西南昌330013；2.江西省新能源工艺及装备工程技术研究中心（东华理工大学），江西南昌330013；3.江西省计量测试研究院,江西南昌330002)

基于超声波多普勒效应的原理通过建立多普勒法测量污水的数学模型，全面分析推导了超声波发射、接受过程中的传导公式，实现了测量多普勒频移来获得了流速[1]、流量的数学公式。在研究多普勒法超声波传输理论的基础上,根据声波动方程的推导分析了超声波信号在介质中的传播衰减特性，得到超声信号的传播衰减特性与介质密度、介质粘度、颗粒尺寸大小和超声波频率有关。通过使用MATLAB软件对超声波在污水模拟介质中衰减进行数值模拟仿真知道，污水的颗粒尺寸、密度和测量使用的超声波频率对超声波回波幅值有重要的影响，很好的印证了理论研究结果。

污水流量测量;超声多普勒;超声波衰减;建模与仿真

在我国经济与工业技术迅速发展的今天，工农业发展的用水量逐年增长，污水排放现象也愈来愈受到重视，环保部门也需要实时监测污水等流体的流量。同时,工业生产中,如冶金、石油、化工等领域都需要严格地控制流体流量，因此对流量计[2]的计量精度和适用条件提出了更高的要求以满足工业需求。而对于特殊污水介质的流量测量显得尤为重要，本文就多普勒方法测量污水的数学建模及其传播特性的影响因素进行了全面的分析，通过数值模拟仿真验证理论研究成果得出结论。完善了理论研究和数学建模，全面分析了多普勒方法测量流体流速和流量的理论研究。

1 连续波多普勒法测量机理建模

图1为连续波多普勒法测量机理[3]示意图，在污水管道两侧相对应的位置上安装超声波发射换能器和超声波接收换能器，管道中流动着携带着散射体（固体颗粒、气泡等）的被测流体，超声波发射换能器发射超声波信号，经介质中的散射体反射后再由超声波接收换能器接受信号。发射换能器发射的一定频率的超声波信号和接受到的超声波信号在图示中信息窗的位置进行叠加，而有效的多普勒信息就体现在该信息窗口处。

图1 连续波多普勒法测量机理示意图

1.1 超声波发射过程数学模型

如图2所示，发射换能器Q1是相对静止的，接收信号的散射体P以速度u运动，发射换能器发射的声源频率为 fs，声源Q1所发出的声振动传播至P1需要经过时间t1，传播至P2需要经过时间t2，根据传播特性的实际情形散射体P行至P1时接收到的声波事实上是其行至时声源Q1所发出的声振动；同理，散射体P行至P2时接收到声波事实上是其行至处时声源所发出的声振动。假设散射体P从运动到P2经过时间Δt，由此得出以下公式：

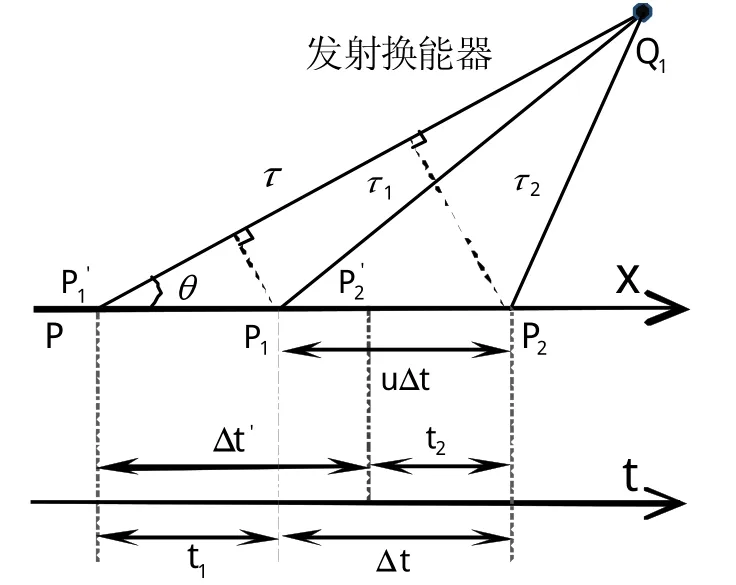
图2 发射过程数学模型示意图

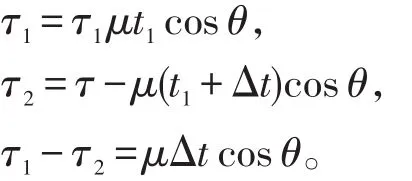
根据分析得到发射换能器发出的声振动的持续时间：

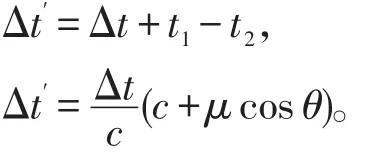
散射体P在时间Δt内接收到声源发射换能器Q1的总振动次数为 fsΔt'，由此可以得到散射体P接收到的声振动频率为：

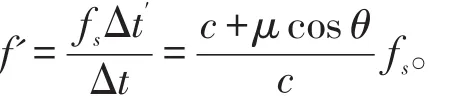
1.2 超声波接受过程数学模型

图3 接受过程数学模型示意图

如图3所示，接受换能器Q2是相对静止的，发射信号的散射体P以速度u运动，接受换能器接受到的频率为 fr，散射体P在P1处所反射的声振动传播到接受换能器Q2需要经过时间t1，经过时间Δt后散射体P运动至P2处，散射体P在R1处所反射的声振动传播至接受换能器Q2需要经过时间t1，由此得出以下公式：

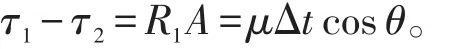
设声源由P1到P2的过程中Q2接收到的声振动的持续时间：

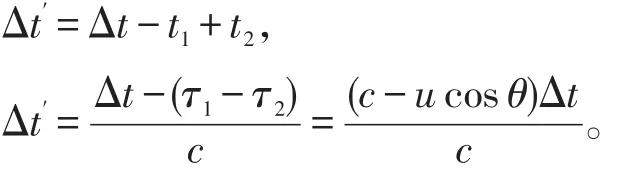
接收换能器Q2在时间Δt'内接收到声源P的总振动次数为 f'Δt，由此得到接受换能器接收到的声振动频率为：

1.3 流速、流量公式的推导

根据上述内容得到悬浮颗粒接收到发射换能器的超声波信号频率如下式：

接受换能器接收到散射颗粒反射的超声波信号频率如下式：

超声波多普勒频移为：

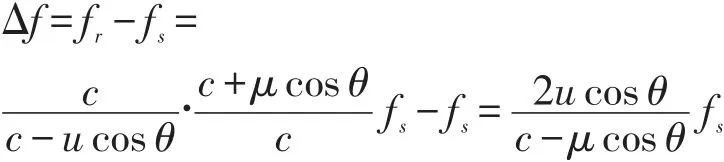
由于超声波的速度c远远大于流体的流速u，因此上式可以化简为：

由此可以反解出流体的流速为：

若设被测管道流通截面积为A，则可以得到流体的体积流量Q为：

通过以上推导可知，当被测流体、流量计参数及管道条件不变时，多普勒频移值与流体流量成正比，所以通过测量多普勒频差，能够获得流体的流速u值和流量Q值[5]。

2 超声波衰减特性影响分析

超声波在介质中的传输一般都是以平面波的形式进行的,也就是说振幅和相位在传输的整个过程中都保持着不变[6]。超声波在介质中传播时，由于介质对超声波的粘滞、热传导、散射以及超声波束自身的扩散作用，使其声能在传输过程中逐渐减弱的现象称之为声衰减。

超声波衰减分成下面四种主要形式：

(1)扩散衰减是由于超声波波束扩散而造成的；

(2)粘滞衰减是由于介质的粘滞性作用而造成的；

(3)热传导衰减是由于介质的其他原因使声能转换为热能而引起的；

(4)散射衰减由于介质中的固体颗粒对超声波的散射而造成的。

扩散衰减[7]是由声源的自身的特性而引起，我们不做研究。而粘滞衰减、热传导衰减[8]和散射衰减主要取决于介质的特性，本文对这三类衰减[9]与幅值的关系进行研究、讨论。

根据声学理论知，粘滞衰减、热传导衰减和散射衰减的表达式都可以用统一的指数方程式来表示，即：

U=U0e-αL，

其中，U0为超声波的初始幅值；U为超声波的回波幅值；L为超声波在介质中传播的距离；a为总的衰减系数。

将上式整理为指数形式为：

由此方程式来更加直观的分析研究衰减与幅值的关系。

由于粘滞衰减系数、热传导衰减系数和散射衰减系数三者之间是相互独立、不相干的所以总的衰减系数可以表示为粘滞衰减系数αη、热传导衰减系数αξ和散射衰减系数αs之和，即：

α=∂η+αξ+αs。

2.1 超声波在介质中传播的粘滞衰减模拟仿真

由波动方程[10]的推导条件推导得到粘滞衰减系数的公式为：

其中，η介质的粘度，单位为Pa⋅s；f超声波的频率，单位为Hz；ρ非均匀介质的密度，单位为Kg/m3；c声速，单位为 m/s。

假设超声波在介质中传播的声速为1800 m/s，非均匀介质的密度为1200 Kg/m3，则其粘滞衰减系数与超声波频率、粘度之间的关系曲线如图4所示。

图4 超声波频率与声粘滞衰减系数的关系

假设超声波在介质中的声速为1800 m/s，超声波频率为700 KHz，则其粘滞衰减系数与介质密度之间的关系曲线如图5所示。

图5 介质密度与声粘滞衰减系数的关系

2.2 超声波在介质中传播的热传导衰减模拟仿真

基尔霍夫导出介质的热传导引起的声衰减系数为：

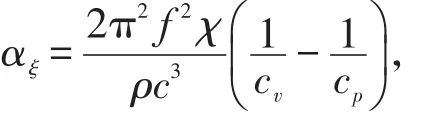
其中，χ热传导系数，单位为W/m⋅℃；cv介质的定容比热，单位为J/kg⋅℃；cp介质的定压比热，单位为J/kg⋅℃；cv=cp/k，k为介质的定压热容比率。

假设热传导系数为0.65 W/m⋅℃，超声波在介质中的声速为1800 m/s，定压比热cp为11000 J/kg⋅℃，定压热容比率k为1.30，则定容比热cv=cp/k=8462J/kg⋅℃。介质密度、超声波频率与热传导衰减系数的关系分别如图6、图7所示。

图6 介质密度与热传导衰减系数的关系

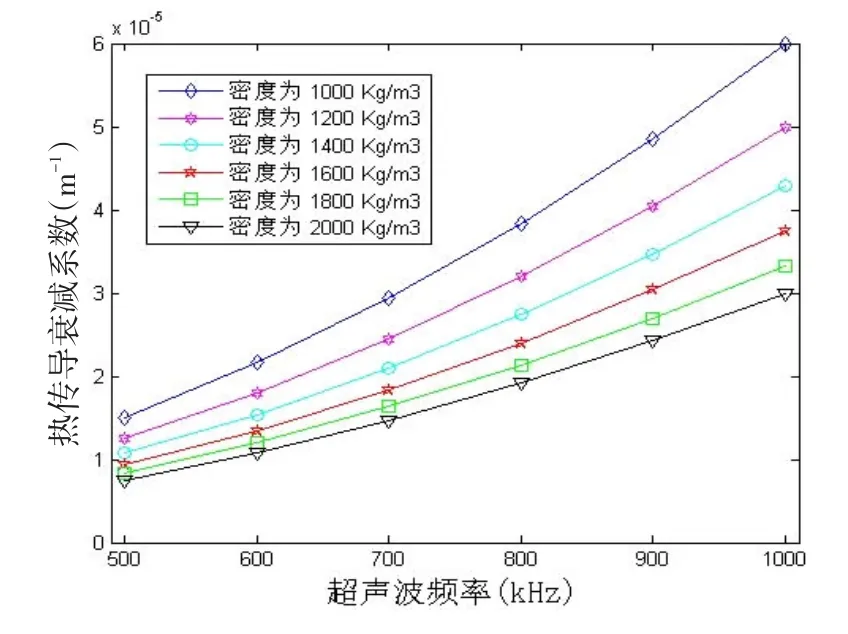
图7 超声频率与热传导衰减系数的关系

2.3 超声波在介质中传播的散射衰减模拟仿真

散射衰减系数[11]的公式为：

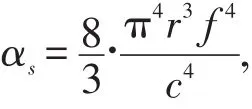
其中，r散射体颗粒粒径，单位为m；f超声波的频率，单位为Hz；c声速，单位为m/s。

假设同样的模拟介质，超声波在介质中的声速为1800 m/s，则超声波频率、介质中颗粒粒径分别与散射衰减系数之间的关系曲线如图8、图9所示。

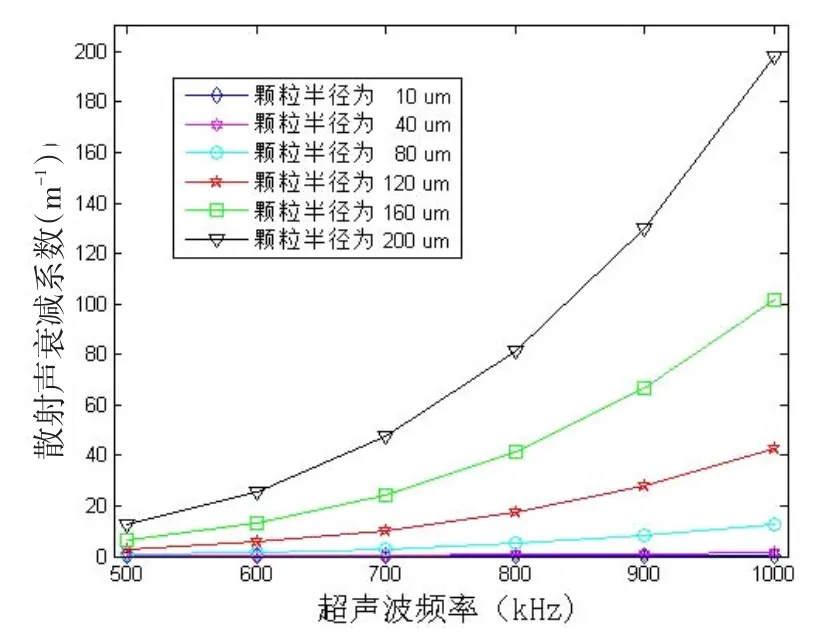
图8 超声波频率与声散射衰减系数的关系

图9 介质颗粒粒径与声散射衰减系数的关系

3 仿真结果分析

通过上述数值模拟的仿真，可以总结得出以下结论：

(1)超声波频率范围在500～1MHz范围内，频率增大，粘滞衰减系数、热传导衰减系数和散射衰减系数都会增大，进而接收到的超声波信号强度变小。

(2)介质的粘度小于0.025 Pa⋅s时，粘度越大，声粘滞衰减系数增大，换能器接收到的超声波信号幅值变小。

(3)介质的密度在1～2g/cm3范围时，随着介质密度的增加，声粘滞衰减系数和热传导衰减系数都减小，进而接收到的超声波信号强度变大。

(4介质中的颗粒粒径在10～200 um范围时,颗粒尺寸越大,其对超声波的散射能力就越强，声散射衰减系数越大，进而接收到的信号幅值就越弱。

超声波在介质中传播时,介质的各个声学特性对超声波信号幅值有着非常重要的影响。而粘滞衰减、热传导衰减、散射衰减这三者之间所占的比重可以通过以下条件的模拟数值进行计算，得出结果如图10所示。

假设超声波在介质中的声速为1800 m/s，介质粘度15 mPa⋅s，介质密度为1200 Kg/m3，超声波频率为500 KHz，热传导系数为0.65 W/m⋅℃，定压比热cp为11000 J/kg⋅℃，定热比率k为1.30，则定容比热cv=cp/k=8462J/kg⋅℃，介质中颗粒半径为80 um。

图10 超声波衰减影响比重

通过对仿真的结果分析得出超声波的散射衰减在三类衰减中的影响比重最大，热传导衰减相比而言，影响微乎其微，所以散射对于回波信号的幅值的影响最为显著。

[1]陈强.超声波流量计的流速测量的研究[D].沈阳：沈阳工业大学，2007.

[2]国家质量监督检验检疫总局，JJ1030-2007《超声波流量计检定规程》[S].

[3]罗守南.基于超声多普勒方法的管道流量测量研究[D].北京：清华大学，2004.

[4]聂世均.超声波在泥浆中的传输规律研究[D].东营：中国石油大学,2007.

[5]杨扬.基于多普勒效应法的超声波流量计的研究[D].南昌：南昌大学信息工程学院自动化系,2007.

[6]马大猷.现代声学理论基础[M].北京：科学出版社,2004.

[7]Mao D H,Zhang Y F,Nie C H.Effects of ultrasonic treatment on structure of roll casting aluminum strip[J].Journal of Central South University of Technology,2007（03）：363-369.

[8]聂世均.超声波在泥浆中的传输规律研究[D].东营：中国石油大学,2007.

[9]张全兴.超声波非均匀介质传播衰减特性研究[D].沈阳：沈阳工业大学信息科学与工程学院,2015.

[10]许肖梅.声学基础[M].北京：科学技术出版社,2003.

[11]胡博.超声波测量河流泥沙含量的算法研究[D].郑州：郑州大学,2005.

Analysis of Mathematical Modeling and Influence Factors of Ultrasonic Sewage Flow Measurement

REN Zeng-qiang1,2,LI Yue-zhong1,2∗,QIAN Yong-an3
(1.School of Mechanical and Electronic Engineering,East China University of Technology,Nanchang Jiangxi,330013；2.Jiangxi Province Engineering Research Center of New Energy Technology and Equipment(East China University of Technology),Nanchang Jiangxi,330013;3.Jiangxi Institute of Metrology&Testing,Nanchang Jiangxi,330002)

Based on the principle of ultrasonic doppler effect,the doppler measurement mathematical model of sewage was built.The ultrasonic transmission and reception in the process of conduction formula was analyzed and deduced.The mathematical formula of flow velocity and flow rate can obtain by the doppler frequency shift measurement.On the basis of studying the ultrasonic propagation attenuation characteristic theory in such special medium for sewage,the attenuation of propagation property is simulated by using MATLAB simulation software.The wave equation of ultrasonic signals spreading in medium water is deduced on the basis of doppler ultrasonic transmission theory.According to the acoustic wave equation,they analyses the ultrasonic signal transmission attenuation characteristic in the medium,and know that the ultrasonic signal transmission attenuation characteristic in the medium is relative to medium density,medium viscosity,particle size and ultrasonic frequency.By using the MATLAB software simulating sewage medium ultrasonic attenuation characteristic,they know that the particle size of sewage and the ultrasonic frequency has an important influence on the ultrasonic amplitude value.The theoretical research results are confirmed by the conclusion of numerical simulation.

sewage flow measurement;ultrasonic doppler;ultrasonic attenuation;modeling and simulating

TH

A

1674-0874(2017)02-0021-04

〔责任编辑 高彩云〕

2016-12-08

国家自然科学基金[61663001]；“江西省新能源工艺及装备工程技术研究中心”开放基金项目[JXNE2015-06]；江西省科技厅科研院所基础设施配套项目[2015BBA13046]

任增强（1989-），男，山西吕梁人，硕士，研究方向：电路系统设计与智能化设备。∗李跃忠，男，教授，通信作者。