二部图的Resolvent Estrada指标的界

乔晓云

(山西大学商务学院，山西太原 030031)

二部图的Resolvent Estrada指标的界

乔晓云

(山西大学商务学院，山西太原 030031)

图G是一个具有n个顶点m条边的(n,m)二部图。图G的EE指标和EEr指标是Estrada引入的图的两个不变量，二部图中有精确的EE(G)指标上下界的范围。在此基础上，得出(n,m)二部图的EEr(G)指标更为精确的上下界。

(n,m)二部图；EEr(G)指标；闭迹个数

图G的Resolvent Estrada指标EEr是E.Estrada和D J Higham在2010年在文献[1]中引入图的不变量，目前关于这个指标的研究很少。D Cvetkovic和M Doob在文献[2]中介绍了二部图的邻接矩阵特征值的一些性质。贾媛媛在文献[3]中得到一般图G，r-正则图以及(n,m)二部图的Estrada指标EE更为精确的上下界。在此基础上，本文得出(n,m)二部图的Resolvent Estrada指标更为精确的上下界。

1 基本概念与引理

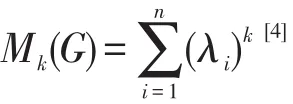
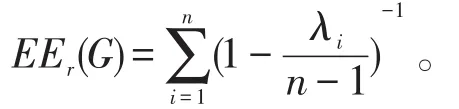
引理1[4]对于任意k≥2，有不等式左边的等号成立当且仅当对于所有的i都有，左边的等号成立当且仅当x=m1且

2 主要结论

定理1对于一个连通二部图G(m,n)（n≥2）它的Resolvent Estrada指标EEr(G)的上下界是：

综上，故原不等式成立。

[1]ESTRADA E,HIGHAM D J.Network properties revealed through matrix functions[J].SIAM,2010(52)：696-714.

[2]CVETKOVIC D，DOOB M.Spectra of graphs-Theory and application[M].Academic Press：New York，1980.

[3]GUTMAN.Estimating the Estrada index[J].Linear Algebra and its Application，2007（427）：70-76.

[4]贾媛媛.若干图的Estrada指标的研究[D].西宁：青海师范大学，2009.

[5]扈生彪，郑国彪.图的特征多项式的若干性质[J].纯粹数学与应用数学，2002，18（4）：90-94.

The Study on Resolvent Estrada Index of(n,m)Bipartite Graph.

QIAO Xiao-yun
(Bussiness College,Shanxi University，Taiyuan Shanxi,030031)

LetGbe(n,m)bipartite graph withnvertices andmedges.Estrada introduced two graph invariants of the Estrada and Resolvent Estrada index ofG,with lower and upper bounds forEE(G)index of bipartite graph.On this basis,we give new lower and upper bounds forEEr(G)index of(n,m)bipartite graph.

(n,m)bipartite graph;EEr(G)Index;the number of close walk

0157

A

1674-0874(2017)02-0012-02

〔责任编辑 高海〕

2016-11-15

山西省社科联重点课题[SSKLZDKT2015088];山西大学商务学院校级科研基金项目[2015035]

乔晓云（1982-），女，山西平遥人，硕士，讲师，研究方向：图论。