基于Java多线程的预处理迭代并行求解器

武瑞婵,邓华丽

（湖北文理学院数学与计算机科学学院，湖北襄阳 441053）

基于Java多线程的预处理迭代并行求解器

武瑞婵,邓华丽

（湖北文理学院数学与计算机科学学院，湖北襄阳 441053）

预处理技术在改善系数矩阵条件数和保证收敛的问题上起到了举足轻重的作用。文中将Java多线程技术与SSOR-PCG算法相结合，设计并实现了一个可交互的并行求解器，为用户的求解过程提供了许多便利。通过算例表明，二者的有机结合可以有效地提高运算效率，同时也可看出运算速度与线程数量并不成正比。

Java多线程；预处理技术；并行计算

对实际问题的数值模拟常常归结为稀疏线性方程组的求解问题，如何提高计算效率一直是这些领域的研究热点，求解的方法也是层出不穷。随着云平台的兴起，并行求解又引发了新一轮的研究热潮[1]，研究成果不断有新的进展，应用的领域也越来越广泛[2]。在迄今为止众多的迭代方法中，超松弛迭代（SSOR）[3]可以通过对参数的调整来改善矩阵的病态特性，预处理共轭梯度法[4]（PCG）在解决对称正定大型稀疏矩阵的问题上不仅具有良好的精度和稳定性，而且还可以使系数矩阵A的特征值分布密集，保证较快的收敛速度。SSOR-PCG算法在文献[5-6]中分别从不同角度对这一理论进行了全方位的论证，卫加宁[3]等还进一步论证了SSOR参数的取值范围。

预处理技术可以改变收敛性，也可以在一定程度上提高运算效率，但若能与多线程并行计算技术进行完美融合，将会使运算效率得到进一步提升。本文将SSOR-PCG算法与Java多线程技术相结合设计和实现了一款并行求解器。计算过程也对串行计算和并行计算的效率进行了详细比较，并使用可视化界面技术将这种计算过程直观化，用户可以通过并行求解器对大型稀疏方程组进行更为方便、有效地求解，极大地方便了用户。最后文章还借鉴了多核环境下的多线程思想[7-8]，旨在寻求更为合适的并行求解模式。

1 并行求解器设计原理

其中D=diag(a11,a22,…,ann)，为系数矩阵A的主对角线元；CL为严格下三角矩阵，它的元素是由A相应部分元素取负号以后构成的。

任取初始向量 x0，则计算得 r0=b-Ax0，z0=M-1r0，p0=z0，对于 k=0,1,…,计算：

2 并行求解器的实现

主要技术：Jsp+css+Sqlserver2005,开发工具：MyEclipse+SQL Server 2005。

求解器所具备的主要功能：导入、输入和随机生成方程组，运用单、多线程来进行计算。

当用户选择“导入已有方程组”并点击时，系统会显示后台数据库中所存放的所有矩阵信息，包括它的阶数，如图1所示。用户可以任意选择待计算的方程组，将系数矩阵的名称填入框内并点击相应计算按钮即可跳转至计算结果界面。界面中详细说明了所计算的矩阵及矩阵的阶数、计算结果、计算方式、计算时间等，用户操作简便，结果清晰明了。

若数据库中没有储存所需计算的系数矩阵，用户则可以点击以上任一界面中的“输入新的方程组”向数据库中添加信息，如图2～4所示。鉴于大型稀疏线性方程组系数矩阵零元素较多的特点，为方便用户输入，计算器在输入新的矩阵时可以忽略零元素，只输入非零元即可。

图1 导入界面

图2 单线程求解界面

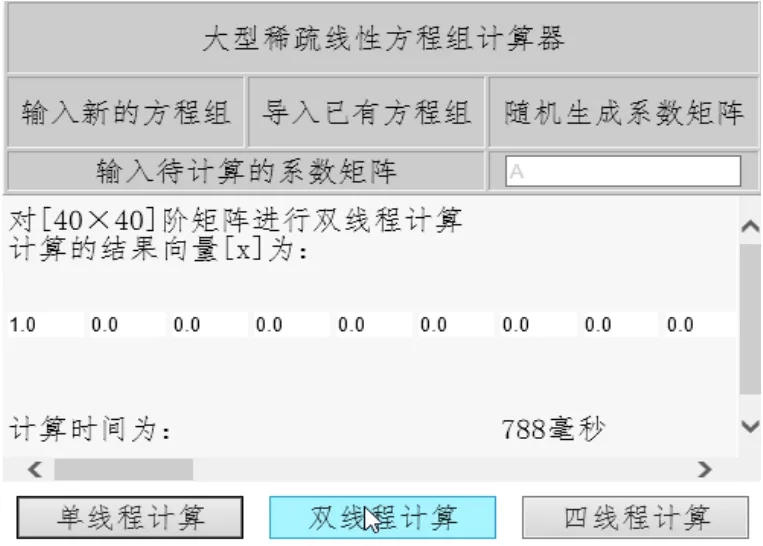
图3 双线程求解界面

图4 四线程求解界面

数据输入完成后，用户可以点击“只存储数据”或“存储并计算”按钮进行相应的操作。若点击“存储并计算”则会得到如图5类似结果。该界面所设计的默认计算是单线程计算，若用户需要计算其它线程的结果，同样可以选择不同的按钮进行计算。

为满足某些理论研究需要，求解器还提供了“随机生成系数矩阵”的功能，如图6。用户只需要输入所求矩阵的阶数即可获得一个随机矩阵，以它作为系数矩阵也可以点击数据存储或存储并计算按钮，其计算过程类似于求解器的前两个功能，这里不再赘述。

图5 输入新的方程组界面

图6 随机生成系数矩阵界面

3 效率分析

以一个40阶的系数矩阵为例如表1～2，通过该计算器来研究多线程并行计算的时间：

表1 某次计算时间

表2 多次平均计算时间

从表1～2可以看出，由于多线程的特性是各线程在排队等待享用CPU资源，因而每次计算顺序和计算时间都不确定。而随着线程分配数目的增多，计算用的时间相应减少，这也说明了利用多线程并行求解确实可以提高运算效率。但是，从无论从单线程到双线程，还是从双线程到四线程，计算时间都不是直接减半。尤其是从双线程到四线程，这种情况体现得尤为明显，这也说明了线程的数量与运算效率并不成比例。

4 小结

在大型稀疏线性方程组的求解中，为了克服系数矩阵病态特性，保证求解过程中的数值稳定性及高效性，本文运用SSOR-PCG算法与Java多线程技术相结合来模拟并行计算，完成了一个求解大型稀疏线性方程组的并行求解器的设计。通过实例计算可知，基于多线程技术的并行计算确实可以提高运算效率，但线程数量与运算效率并不成正比。不足的是，大型稀疏矩阵的多样化决定了本文研究的片面性，本文并没有找到一个适合所有大型稀疏线性方程组求解的方法。而且并行算法的设计模式也具有多样性，同样值得深入研究。

[1]刘师范.并行计算方法研究与应用[J].数字技术与应用,2014(1)：109-110.

[2]张冬姣,孟庆伟,王萍.基于Java多线程的并行计算技术研究及应用[J].科学中国人,2014（10）：15-16.

[3]卫加宁,武瑞婵.预处理迭代的性质及其应用[J].武汉理工大学学报(交通科学与工程版),2006,30(4)：646-648.

[4]刘盎然.线性方程组的迭代和最速下降法[J].赤峰学院学报(自然科学版),2014(2)：10-13.

[5]薛秋芳.解线性方程组的几种迭代法的收敛性分析[D].西安：陕西师范大学,2014.

[6]KURDI YEl,GROSS W J,GIANNACOPOULOS D，et al.Parallel Multigrid Acceleration for the Finite-Element Gaussian Belief Propagation Algorithm[J].IEEE Transactions on Magnetics,2014,50(2)：7014304-1-7014304-4.

[7]王晗.基于多核环境下的多线程并行程序设计方法研究[D].郑州：中原工学院,2014.

[8]冯佩,钟诚,韦伟.多核多线程并行求解线性方程组[J].合肥工业大学学报(自然科学版),2011(2)：237-240.

Parallel Solver about the Preconditioned Iterative Based on the Java Multithread

WU Rui-chan,DENG Hua-li
(School of Mathematical and Computer Sciences,Hubei University of Arts and Science,Xiangyang Hubei,441053)

The pretreatment technology is very important to improve the condition number of coefficient matrix and ensure its convergence problem.In this paper,an interactive parallel solver is designed;it will offer many convenient for the user.The technology of this solver is Java multi-thread and SSOR pretreatment iterative.Numerical example shows that the efficiency of operation can be improved effectively by using these technologies,but the computing speed is not proportional to the number of threads.

java multithread;preconditioned;parallel computing

O245

A

1674-0874(2017)02-0009-03

〔责任编辑 高海〕

2016-11-15

国家自然科学青年基金资助项目[71501064]

武瑞婵（1978-），女，山西昔阳人，硕士，讲师，研究方向：计算数学。