诱导Banach代数及其表示

黄利忠，石岩岭

（1.山西大同大学数学与计算机科学学院，山西大同037009；2.山西大同大学网络信息中心，山西大同037009）

诱导Banach代数及其表示

黄利忠1，石岩岭2

（1.山西大同大学数学与计算机科学学院，山西大同037009；2.山西大同大学网络信息中心，山西大同037009）

基于Banach代数动力系统,提出了诱导Banach代数的定义,证明了Banach代数的不可约有界表示蕴含着诱导Banach代数的不可约有界表示,最后探讨了连续函数空间稠密子代数的结构特征。

G-空间;诱导Banach代数;表示

在量子物理中,C*-动力系统经常被用来描述时间演化和可见的空间转化。因而交叉积理论在量子物理学及其它学科中有着广泛的应用。D.P.Williams的专著“Crossed Products ofC*-Algebras”[1]对C*-代数交叉积近年来的发展做了详细且系统的描述,提出了一些新的问题,极大地推动着交叉积理论的发展。在文献[2],S.Dirksen探讨了Banach代数动力系统的非退化的连续共变表示与相应的Banach代数交叉积的非退化有界表示之间的关系，随后又证明了交叉积代数与广义Burling代数是拓扑同构的[3]。基于理论和应用的重要性,一大批数学学者投身于交叉积的研究,得到了丰富而深刻的结果[3-6]。

设A是Banach代数,我们用Aut(A)表示A上等距自同构映射构成的全体。称三元序组(A,G,α)是一个Banach代数动力系统,其中A是一个Banach代数,G是局部紧的Hausdorff群,α：G→Aut(A)是G在 A上的强连续表示。 在C*-代数的情形下,由于每个动力系统都可在A的本原理想空间Prim A上产生一个G-作用,故考虑给定集合上的G-作用及相关问题是有意义的。本文在Banach代数动力系统和G-空间的基础上,给出诱导Banach代数的概念,对其结构做了初步探讨,证明了若Banach代数A上的表示是有界不可约的,则诱导Banach代数(A,G,α)上的表示也是有界不可约的,最后我们研究了映到(A,G,α)的稠密子代数Ccc(Y,Indcα)的结构特征。

1 诱导Banach代数

设X是一个(左)G-空间,x∈X,一般我们称集合 G·x：={s·x∈X,s∈G 且 x∈X}是过 x点的轨道。在 x点处的稳定群是指 Gx：={s∈G：s·x=x}。对任意的x∈X,若Gx={e},则称G-作用是自由的。轨道的集合记为X G,自然映射 p：X→X G称为轨道映射,若轨道空间赋予商拓扑,则称X G为轨道空间。轨道空间X G中元素的等价关系定义为：对任意的 x,y∈X,x≠y,x～y当且仅当G·x=G·y。一般,轨道映射 p是连续的开映射.称局部紧的G-空间P 是真的,若映射 (s,x)↦(s·x,x)是一个从 G×P 到P×P的一个真映射。任何紧群的作用都是真作用。一般地,如果P是一个真的局部紧的G-空间,则P G是一个局部紧的Hausdorff空间。

定义1设(A,G,α)是Banach代数动力系统,P是一个左G-空间。令

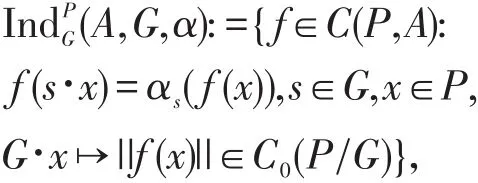
由于α是G在A上的连续同态,映射x↦||f(x)||在G-轨道上是常数,这样G·x↦||f(x)||是有意义的。从定义上易知(A,G,α)是一个Banach代数,同时若A是对合的,则(A,G,α)也是对合的。当P是右G-空间时,我们可定义

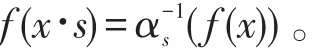
定理1设G是自由真作用于局部紧空间P的右边的局部紧群,(A,G,α)是Banach代数动力系统。若对任意的 f∈Cc(P),a∈A,f·a(x)= ∫Gf(x·s)αs(a)/u(s),则 f·a是诱导Banach代数(A,G,α)中定义良好的元。

证明由于G在P上的作用是真的,对任意给定的 x, 集合{s：x·s∈sup p(f)}(其中 supp(f)表示 f的支集)是紧的。显然 f(x·s)αs(a)属于Cc(G,A),因此f·a 定义良好。下证对任意的

若{xi}i∈D(D为指标集)是P中收敛于x的网,则存在x的一个紧邻域K,存在N∈D,当i＞N时,xi∈K 。令表示空集),则L是紧集。由 f的一致连续性,对任意的ε＞0,存在x的一个紧邻域K0,当y∈K0时,有|f(y)-f(x)|＜ε。

此 时若 s∈L,一 定 有 |f(y·s)-f(x·s)|＜ε 。 而xi∈K0,所以

从而 f·a在 P上是连续的。 要证 x·G→||f(x)||∈C0(P G),只需说明

而||f·a(·G)||一定在无穷远处趋于零,这是显然的。所以 f·a是(A,G,α)中定义良好的元。

推论1设(A,G,α)是Banach代数动力系统,其中G是自由真作用于局部紧空间P左边的局部紧群,则对任意的 f∈Cc(P),a∈A,

定理2设(A,G,α)是Banach代数动力系统,其中G是自由真作用于局部紧空间P左边的局部紧群,π0是 A在Banach空间X上的不可约有界表示。若π(A,G,α)→B(X)定义为：

证明对任意的 f,g∈(A,G,α),λ,η∈K,

所以π是有界的。

于是,

2 子代数Indcα

定理3设(A,G,α)是Banach代数动力系统,Y是局部紧空间,P是局部紧的G-空间。令Ccc(Y,Indcα)是C(Y×P,A)中满足下列条件的函数族{f}：

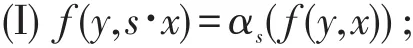
(II)存在紧集C⊂Y,T⊂P G,使得若 (y,G·x)≠ C×T,则 f(y,x)=0 。则映射 y↦f(y,·)属于Cc(Y,Indα);若将 Ccc(Y,Indcα)视为 Cc(Y,Indα)的子代数,则 Ccc(Y,Indcα)在 Cc(Y,Indα)中按归纳极限拓扑意义下是稠密的。

证明首先 f(y,·)∈Indα 。若映射 y↦f(y,·)不连续,则存在 ε＞0,对Y中收敛于 y的网{yi},||f(yi,·)-f(y,·)||≥ε。注 意 到 f(y,·)∈Indα , 故 存 在{xi}⊂P,使得 ||f(yi,xi)-f(y,xi)||≥ε 。又因为 f∈Ccc(Y,Indcα),故{G·xi}⊂T ，于是有收敛的子网。 所以对P中的元素x,存在si∈G,使得xisi→x。进而

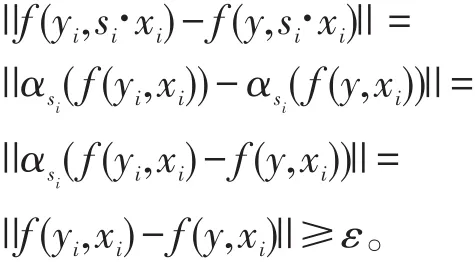
若将Ccc(Y,Indcα)视为 Cc(Y,Indα)的子代数,为证Ccc(Y,Indcα) 在 Cc(Y,Indα) 中 的 稠 密 性, 可 设z∈Cc(Y), f∈Indcα。由于 Cc(Y)⊗Indcα 在 Cc(Y,Indα)中按归纳极限拓扑是稠密的,且Indcα在Indα中稠密的,故 z⊗f∈Cc(Y,Indα)。定义

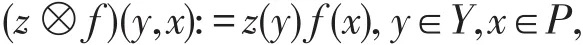
则 (z⊗f)(y,s·x)：=z(y)f(s·x),且支集 supp(z⊗f)包含在某个紧集中,这表明z⊗f∈Ccc(Y,Indα)。

推论2设(A,G,α)是Banach代数动力系统,Y是局部紧空间,P是自由的真的局部紧的G-空间。若F∈Cc(Y×P,A),则

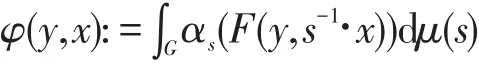
定义了Ccc(Y,Indcα)中的元素φ。

[1]WILLIAMS D P.Crossed products ofC*-algebras[M].Mathematical Surveys and Monographs：American Mathematical Society,Providence,RI,2007.

[2]DIRKSEN S,JEU M D,WORTEL M.Crossed products of Banach algebras，I[J].arXiv：1104,5151(2011).

[3]DE M JEU,MESSERSCHMIDT M,WORTEL M.Crossed products of Banach algebras，II[J].arXiv：1305,2304(2013).

[4]HUANG L,LU F.Reduced crossed products associated with Banach algebra dynamical systems[J].Integr.Equat.Oper.Th,2016,84(4),451-462.

[5]BEDOS E,KALISZEWSKI S,QUIGG J,etal.A new look at crossed product correspondences and associatedC*-algebras[J].J Math Anal Appl,2015,426(2)：1080-1098.

[6]GIORDANO T,SIERAKOWSKI A.Purely infinite partial crossed products[J].J Funct Anal,2014,266(9)：5733-5764.

[7]RAEBURN I,WILLIAMS D P.Morita equivalence and continuous-traceC*-algebras[M].American Mathematical Society,Providence,RI,1998.

Induced Banach Algebra and Its Representations

HUANG Li-zhong1,SHI Yan-ling2
(1.School of Mathematics and Computer Science,Shanxi Datong University,Datong Shanxi,037009;2.Network Information Center,Shanxi Datong University,Datong Shanxi,037009)

Based on Banach algebra dynamical system,the notion of induced Banach algebra is given.We show that if the representation of given Banach algebra is irreducible bounded,then the representation of the associated induced Banach algebra is also irreducible bounded.We study the structure of a dense subalgebra of continuous function space.

G-spaces;induced Banach algebras;representations

O177.5

A

1674-0874(2017)02-0001-03

〔责任编辑 高海〕

2016-12-16

国家自然科学基金青年科学基金资助项目[11301312];山西大同大学博士科研项目[2015-B-09]

黄利忠(1980-),男,山西代县人,博士,讲师，研究方向：算子理论与代数。