抽样法与灵敏度法keff不确定度量化∗
胡泽华1)2)† 叶涛1)2) 刘雄国1)2) 王佳1)2)
1)(北京应用物理与计算数学研究所,北京 100094)2)(中国工程物理研究院高性能数值模拟软件中心,北京 100088)(2016年7月7日收到;2016年9月30日收到修改稿)
抽样法与灵敏度法keff不确定度量化∗
胡泽华1)2)† 叶涛1)2) 刘雄国1)2) 王佳1)2)
1)(北京应用物理与计算数学研究所,北京 100094)2)(中国工程物理研究院高性能数值模拟软件中心,北京 100088)(2016年7月7日收到;2016年9月30日收到修改稿)
核反应堆的中子学模拟计算中,核数据的不确定度导致的积分量计算结果的不确定度,通常采用基于微扰理论的灵敏度与不确定度分析方法(简称灵敏度法)量化.灵敏度分析法原则上只适用于线性模型,且一般输运计算程序难以直接进行灵敏度分析.而抽样法直接抽样核数据输入中子学计算程序进行计算,通过对计算结果的统计分析评估计算量的不确定度.抽样法易于实现、计算精确、且适用性强.在灵敏度分析与不确定度量化程序SURE中,增加了抽样法不确定度的量化功能.为将抽样法不确定度量化应用于复杂问题的模拟计算,需对其进行细致的考核.为此,选取简单的临界基准实验模型,分别采用灵敏度分析法和抽样法进行不确定度量化,得到了各核素各反应道核数据导致的keff计算不确定度.对比显示,两种方法的不确定度计算结果有很好的符合,验证了SURE程序抽样法功能的正确性.抽样法计算的keff符合正态分布,说明在一般核数据的不确定度范围内,keff与核数据近似成线性关系,利用灵敏度分析法评估keff计算值的不确定度是适用的.
不确定度量化,随机抽样法,灵敏度,核数据
1引 言
数值模拟是目前核反应堆工程设计与安全分析的重要基础,而不确定度是计算结果可信度的量度.在核反应堆工程领域,安全性是需要关注的首要问题;而经济性则决定了商业核电的竞争力.科学量化模拟计算的不确定度,对合理平衡核工程设计的安全性与经济性具有重要的意义,因而越来越受到关注.随着新型反应堆(GEN-IV)[1]研究与实验的发展,对反应堆数值模拟不确定度量化的可靠性与精度提出了更高的要求[2].发展可靠的反应堆数值模拟的不确定度分析方法,对提高数值模拟的可信度十分必要.
模拟计算的不确定度源自多方面因素,而输入数据(如系统的物质性质、几何尺寸)引入的不确定度是其中的重要部分.源自输入数据的不确定度属认知不确定度,已经发展了多种方法进行不确定度量化(简称UQ).这些方法大致可分为两类:确定论方法和随机统计方法.两者的主要区别在于:确定论方法基于对计算模型的简化近似进行,只在一定范围内适用,计算速度快;而统计方法在理论上是精确的,但需要进行大量的计算,基本上是普适的.
在反应堆领域,常用的确定论UQ方法有:传统的基于一阶微扰近似的灵敏度与不确定度(S/U)分析方法[3]和最近引入的多项式混沌展开(PCE)方法等[4].灵敏度分析方法在核反应堆的中子学计算中有长期的广泛应用[5−9].S/U分析方法基于一阶微扰近似计算响应量对核数据等输入参数的灵敏度系数S,再利用线性近似的不确定度传递公式,由S结合核数据的协方差得到核数据导致的积分响应量计算不确定度.灵敏度分析方法可用于分析中子有效增殖因数(keff)、反应率等响应量的不确定度,计算速度快,在一定范围内结果也比较可靠,但难以普遍适用于多物理复杂问题计算的不确定度量化.近几年,在流体力学和结构力学等领域广泛应用的PCE方法也被引入核数据评价[10]以及反应堆计算的不确定度分析[4,11,12].相比基于微扰的灵敏度分析法,PCE方法计算量大,但适用性较好.
随机统计法不确定度量化,通常称为Monte Carlo(MC)法或抽样方法,通过对问题进行一系列的模拟,统计得到计算结果的不确定度.抽样方法UQ,除去统计不确定度(可通过增加抽样次数降低)外是精确的,是普适的UQ方法,但是所需的计算量大.近来,随着计算能力的快速提升,多种基于随机抽样的UQ方法逐步发展,并得到较广泛的应用[13−16].随机抽样法在模拟计算的随机输入参数空间内进行抽样,获取系列随机参数组,将各参数组代入计算程序中完成计算,得到系列计算结果;通过对计算结果的统计分析得到期望值与方差.抽样法不需要了解模拟计算过程,可将计算过程视为“黑箱”,因此易于实现;但抽样法要进行多次模拟计算以得到收敛的结果,需要大量的计算时间.
灵敏度分析与不确定度量化程序SURE[9],基于微扰理论发展了keff、反应性系数等积分量对全套核数据的灵敏度分析功能;利用灵敏度系数结合协方差数据,量化核数据导致的积分量计算不确定度.通过与直接法计算和成熟程序[8]的对比,SURE程序的灵敏度分析与不确定度量化功能,已得到比较充分的验证.为拓展SURE程序不确定度量化的适用范围,发展了随机抽样法不确定度量化功能.在将抽样法应用于实际复杂问题的不确定度量化前,为保证可靠性,需对SURE中实现的抽样法功能的可靠性进行比较充分的验证.由于灵敏度分析法不确定度量化是基于线性近似的,其适用范围也值得细致考查.
本文通过与传统的灵敏度法不确定度计算结果的对比,验证SURE中新发展的抽样法不确定度量化功能的正确性.鉴于抽样法是“精确”的UQ方法,通过两种方法计算结果的对比,也考察了基于线性近似的灵敏度法不确定度量化的适用性范围.本文的第2部分介绍核数据及其协防的基本概念,以及计算中所采用的核参数和程序;第3部分介绍灵敏度法和抽样法不确定度量化理论;第4部分介绍计算分析采用的两个基准实验模型;第5部分给出灵敏度分析法和抽样法的不确定度量化结果;最后给出结论.
2核数据与输运计算
2.1 核数据及其协方差
核(反应)数据主要描述粒子与原子核发生反应的概率(以截面表述),以及反应后出射粒子的能量和角度分布信息(以双微分截面表述)等,是中子输运问题计算的主要输入参数,也是计算不确定度的主要来源.核数据主要基于实验测量数据评价得到,其真值是未知的,应视为服从正态分布的随机量.最新的评价核数据库[17],不仅包含核数据的期望值,还包含协方差.核数据的协方差描述核数据的不确定度及数据间的关联,是进行不确定度量化的基础数据.核数据σi的期望值与协方差cov(σi,σj)构建了核数据的联合概率分布,可视为多维正态分布.
2.2 输运计算与核数据处理
本文对比考察灵敏度分析法与随机抽样法的keff不确定度量化,分别利用SURE程序的灵敏度分析模块Sensitivity和抽样模块Sample进行计算.灵敏度分析法需分别进行一次输运计算和伴随输运计算,得到通量和伴随通量;抽样法需进行多次输运计算,以统计keff计算结果.两方法中均采用一维多群SN输运程序ANISN[18]进行输运计算.
输运计算所需的多群输运核数据,灵敏度分析所需的多群核反应截面与分反应道群转移矩阵,以及不确定度量化所需的多群协方差数据,均采用NJOY[19]的172群结构,基于ENDF/B-VII.1评价库[17]的中子核数据制作而成.图1为235U的核数据的部分协方差,图1(a)为非弹散射截面172群协方差;图1(b)为辐射俘获截面协方差;图1(c)为弹散截面与非弹散射截面间的协方差;图1(d)为裂变截面与俘获截面间的协方差.

图1 (网刊彩色)235U核数据的172群核数据协方差 (a)非弹散射;(b)辐射俘获;(c)非弹散射-弹散;(d)裂变-辐射俘获Fig.1.(color online)172group covariance data for235U nuclear data:(a)Inelastic scattering;(b)radiative capture;(c)inelastic scattering-elastic scattering;(d) fi ssion-radiative capture.
3keff的不确定度量化方法
分别简述传统的基于微扰理论灵敏度分析的keff模拟计算不确定度量化方法和近来得到广泛应用的基于随机抽样的不确定度量化方法.
3.1 灵敏度分析法
灵敏度分析法不确定度量化通过一次输运计算和一次伴随输运计算得到中子角通量和伴随角通量,再基于微扰理论得到keff计算对全套核数据的灵敏度系数;由灵敏度系数结合协方差,计算核数据不确定度导致keff计算的不确定度.
模拟计算中,灵敏度指输入参数变化导致的输出量(计算结果)的变化量,(相对)灵敏度系数(sensitivity coefficient)SR,α定义为输出量的相对变化量与导致其变化的输入量相对变化量之比:

其中,R为模拟计算的输出量(响应量、积分量),α为计算的输入参数(如核数据、核素丰度等).
记λ=1/keff,根据一阶微扰理论,keff计算对核数据的灵敏度系数表示为

其中,ϕ为ϕ(r,E,Ω)的简写,由keff本征值输运方程
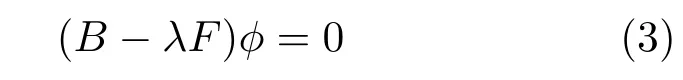
计算得到;ϕ∗为ϕ∗(r,E,Ω)的简写,由keff本征值伴随输运方程

计算得到;B和F分别为输运算符和裂变算符,分别表示为
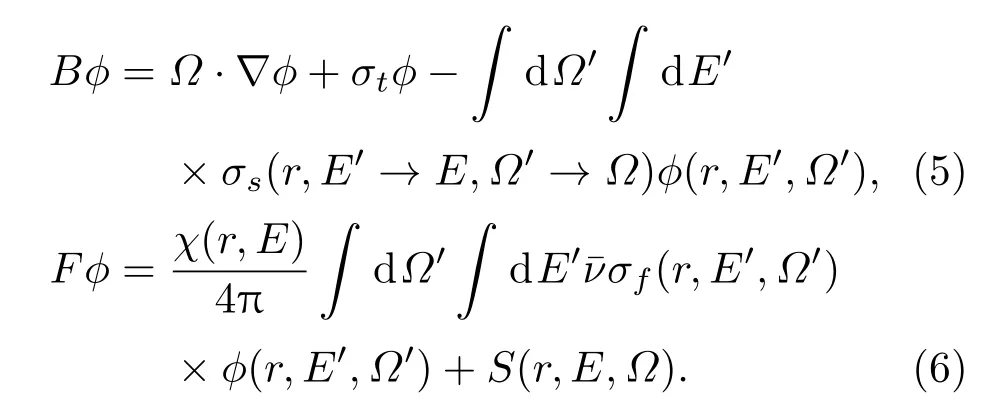
可见,求得角通量和伴随角通量,即可由(2)式得到keff对核数据的灵敏度系数.一般利用确定论多群SN离散坐标输运方法,进行一次输运计算和一次伴随输运计算,求解通量和伴随通量.近来发展了基于连续能量MC计算的伴随通量统计方法[20],进行keff对连续能量核数据的灵敏度分析.本文采用多群SN方法进行输运和伴随输运计算.
假定keff计算值与核数据间是线性关系,利用灵敏度系数结合协方差数据,由不确定度传递公式

即可量化keff计算的不确定度,其中,σi为第i个核数据,Sk,σi为keff对核数据的灵敏度系数,Cσi,σj为核数据间的协方差矩阵.
3.2 随机抽样法
一般可将多群SN输运计算中使用的N个核数据的随机分布视为N维正态分布,利用核数据的期望值σi(i=1,N)及其协方差C(σi,σj)可建立核数据的N维正态分布空间.
若考虑其中的n(n≤N)个核数据,核数据及其期望值组成的列矩阵分别记为

协方差矩阵记为C,则n个核数据的概率密度分布为
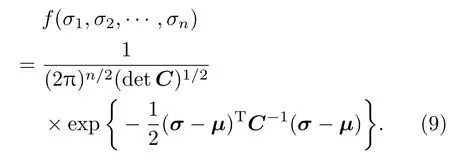
为在n维正态分布空间内进行随机抽样,首先对协方差矩阵C进行奇异值分解,得到T矩阵,使得

再从标准正态分布中抽样n个随机数,记为Z,则的核数据抽样为

在核数据的随机分布空间进行抽样,每次抽样得到一套核数据,将抽样核数据输入计算程序,得到一个keff计算值.进行M次抽样,计算得到M个keff值.通过对keff计算结果进行统计分析,得到keff计算的期望值和方差:

与灵敏度分析法不同,抽样法不需要假定keff与核数据间成线性关系.由于抽样法不需线性假定,且可将计算程序视为“黑箱”使用,因而抽样法不但计算精确,而且具有更广泛的适用性.
抽样法中,在量化某一反应道数据导致的不确定度时,在该反应道数据随机分布内抽样,统计计算结果的标准差;在量化两反应道关联导致的不确定度Uc时,首先在两反应道核数据的联合随机分布内进行抽样,得到keff不确定度量化值U0,再分别独立量化两反应道数据导致的不确定度U1和U2,利用下式

得到反应道关联导致的不确定度.
4基准实验模型
由于抽样法不确定度量化,需进行大量的模拟计算,计算时间消耗大.为节约时间,选取了简单的基准实验模型Godiva和Jezebel[21]进行计算.Godiva和Jezebel都是美国洛斯阿拉莫斯国家实验室开展的临界积分实验.Godiva为球形高浓铀(235U)裸临界基准装置,半径为8.7407cm,keff的基准实验值为1.0±0.001;Jezebel-239Pu为球形239Pu裸基准装置,半径为6.38493cm,keff的基准实验值为1.0±0.002.两装置的核素成分见表1.

表1 Godiva和Jezebel的核子数密度Table 1.Atom densities for the Godiva and Jezebel Benchmark.
5计算分析
利用SURE程序的灵敏度分析模块和抽样模块,分别对基准模型Godiva和Jezebel,计算了各核素的弹散(n,n)、非弹(n,n′),n 2n(n,2n)、裂变(n,f)和辐射俘获截面(n,gamma),以及平均裂变中子数(nubar)导致的keff计算不确定度.
5.1 Godiva基准实验模型
通常的输运计算,直接采用核数据的期望值.采用制作的172群核数据(期望值),计算的Godiva基准实验的keff为1.0006;采用随机抽样法,抽样10000组核数据(这里主要是为了考察keff计算的分布规律进行了10000次抽样,实际的抽样法量化中,并不必要进行这么多次抽样计算),计算得到keff期望值(平均值)为1.0010,两者相差仅为4×10−4,符合很好.采用灵敏度法量化的全部核数据导致的keff计算不确定度为1.206%,采用抽样量化为1.212%,两者相差6×10−5,符合得很好.
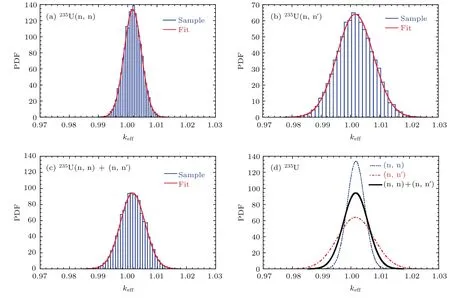
图2 (网刊彩色)Godiva基准模型抽样法不确定度量化I(PDF为概率密度函数) (a)弹散截面导致的keff计算值分布;(b)非弹截面导致的keff计算值分布;(c)弹散与非弹截面导致的keff计算值分布;(d)三者对比Fig.2.(color online)Uncertainty quanti fi cation using sampling method for Godiva Benchmark I(PDF is probability density function):(a)keffdistribution due to elastic cross sections;(b)keffdistribution due to inelastic cross sections;(c)keffdistribution due to elastic and inelastic cross sections;(d)comparison of the three cases.
进一步采用抽样法分别量化各核素各反应道截面数据导致的Godiva基准实验的keff计算不确定度,每次计算抽样10000次.如图2所示,图2(a)—(c)为keff抽样计算值分布直方图与keff抽样计算的平均值与标准差u为参数的正态分布曲线.图2(a)和图2(b)分别给出了235U的弹性散射截面与非弹性散射截面的随机分布导致的keff计算值分布;图2(c)给出了235U的弹性散射截面与非弹性散射截面的联合随机分布导致的keff计算值分布.可见,三种情况下,keff计算值的随机分布均很好地符合正态分布.由于截面由正态分布抽样得到,keff分布符合正态分布表明在三种情况下截面的抽样扰动值与keff计算扰动值基本符合线性关系.图2(d)给出了三种情况下keff分布拟合正态分布曲线.可见,弹散截面导致的keff计算不确定度最小,非弹导致的不确定度最大,弹散与非弹共同导致的不确定度介于两者之间.这是由于弹散与非弹截面间是负相关(如图1(c)),而弹散与非弹截面主要有正的灵敏度系数,因而其对不确定度的贡献为负值.
图3对比了235U的裂变截面、辐射俘获截面以及裂变-辐射俘获截面联合分布下的keff抽样计算结果.图3(a)—(c)分别为裂变、辐射俘获和裂变-辐射俘获截面随机分布下keff抽样计算值分布直方图与keff抽样计算的平均值与标准差u为参数的正态分布曲线,图3(d)给出了三种情况下keff分布拟合正态分布曲线.可见,裂变与俘获截面共同导致的keff计算不确定度最大,其次为俘获截面.裂变截面与俘获截面基本上是负相关(如图1(d)),但裂变截面有正的灵敏度,俘获截面为负的灵敏度,两者的关联对不确定度的贡献为正.俘获截面的抽样扰动值仍与keff计算扰动值也基本符合线性关系.
利用MATLAB软件的normplot命令分别绘制了弹散截面和俘获截面抽样的keff计算值的正态概率分布图,分布点越接近直线越符合正态分布.如图4所示,两种情况下keff分布均基本符合正态分布,只是不确定度较大的俘获截面抽样的keff分布略偏离正态分布一些.
采用灵敏度分析法,先计算keff对各核数据的灵敏度系数,再结合协方差数据,利用不确定度传递(7)式,计算了各核素各反应道截面不确定度导致的keff的不确定度.抽样法与灵敏度法量化的keff不确定度的对比见表2.

图3 (网刊彩色)Godiva基准模型抽样法不确定度量化II (a)裂变截面导致的keff计算值分布;(b)俘获截面导致的keff计算值分布;(c)裂变与俘获截面导致的keff计算值分布;(d)三者对比Fig.3.(color online)Uncertainty quanti fi cation using sampling method for Godiva Benchmark II(PDF is Probability Density Function):(a)keffdistribution due to fi ssion cross sections;(b)keffdistribution due to capture cross sections;(c)keffdistribution due to fi ssion and capture cross sections;(d)comparison of the three cases.
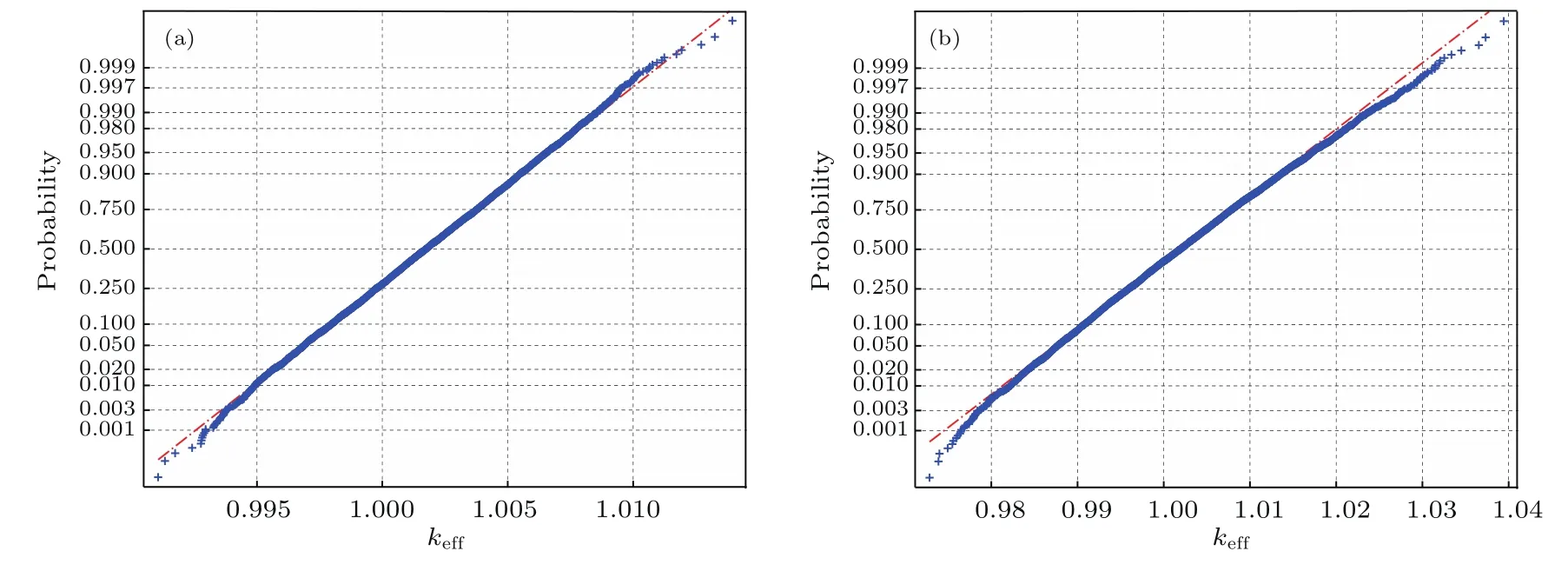
图4 (网刊彩色)正态概率分布 (a)弹散截面抽样的keff分布;(b)俘获截面抽样的keff分布Fig.4.(color online)Normal probability distribution:(a)keffdistribution due to elastic cross sections;(b)keffdistribution due to capture cross sections.
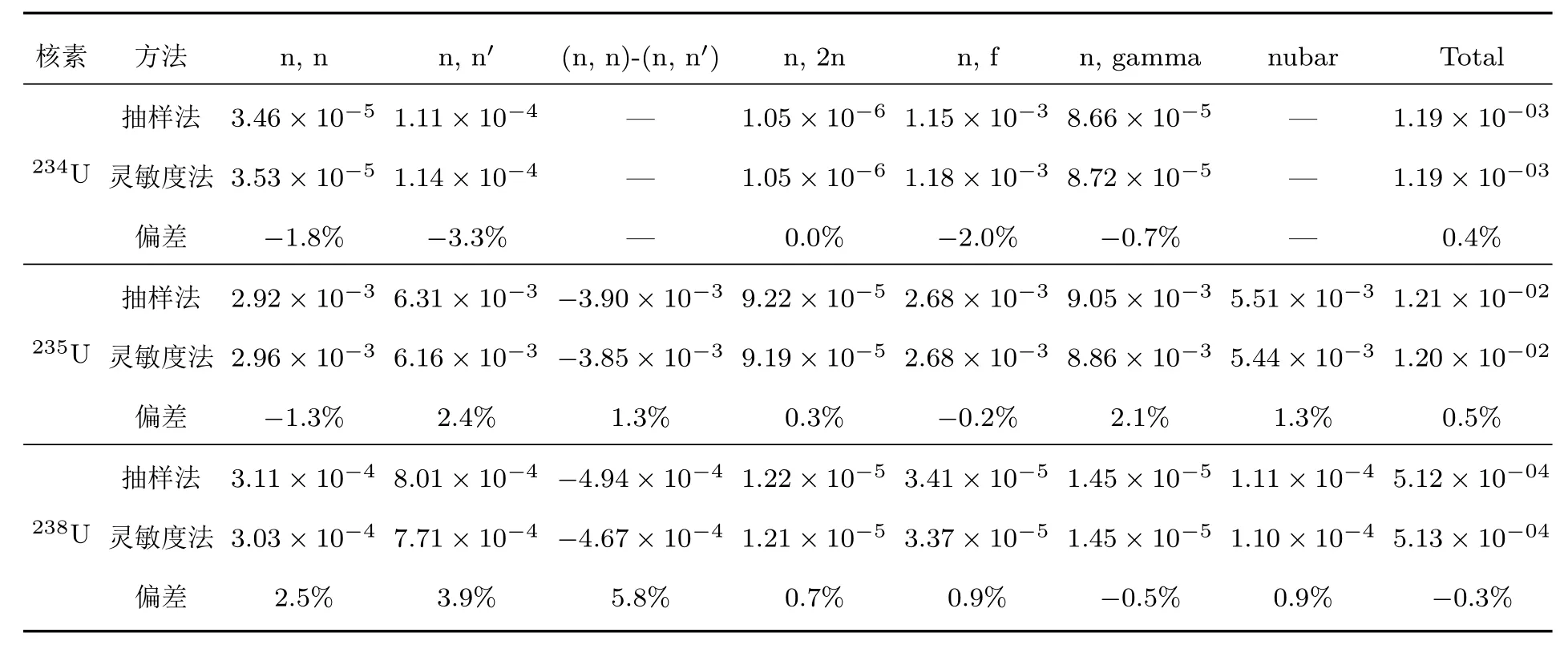
表2 各核素各反应道核数据导致的Godiva模型keff计算不确定度Table 2.Uncertainties of kefffrom every nuclides and every reaction types for Godiva.
可见,对各核素各反应道,采用灵敏度分析法和抽样法得到的keff计算不确定度量化结果,均有很好的符合,最大偏差<6%.SURE程序灵敏度分析法不确定度量化结果已通过与成熟程序(TSUNAMI,SUSD等[5])结果比较得到充分的验证.抽样法不确定度量化结果与灵敏度法结果符合很好,一方面表明SURE抽样法不确定度量化结果的可靠性,另一方面也进一步印证了灵敏度法量化的可靠性.
鉴于灵敏度法中采用的不确定度传递公式是基于输入数据与计算结果间是线性关系的假定,灵敏度法与抽样法的结果符合很好也显示对Godiva模型的计算,在核数据协方差的扰动范围内,keff计算值与核数据成线性关系.
5.2 Jezebel基准实验模型
采用核数据期望值,计算的Jezebel基准实验的keff为0.99996,采用随机抽样法计算得到keff期望值为1.0001,两者相差仅为1.4×10−4,符合得很好.进一步,采用灵敏度分析法和抽样法分别量化各核素各反应道截面数据导致的Jezebel基准实验的keff计算不确定度,结果见表3.
可见,与Godiva模型计算相似,对各核素各反应道,采用灵敏度分析法和抽样法得到的keff计算不确定度量化结果均有很好的符合,最大偏差仅为2.3%.
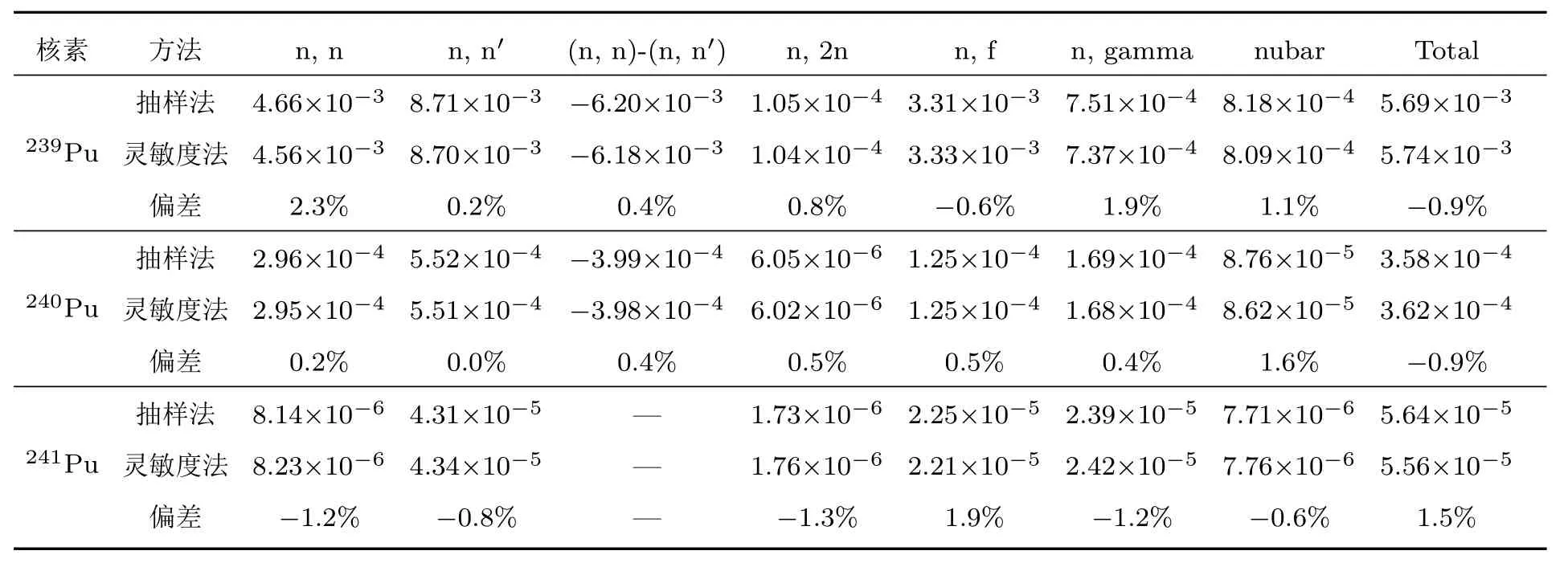
表3 各核素各反应道核数据导致的Jezebel模型keff计算不确定度Table 3.Uncertainties of kefffrom every nuclides and every reaction types for Jezebel.
6结 论
分别采用SURE程序的灵敏度分析方法和随机抽样方法,对两个典型临界基准实验Godiva和Jezebel,计算了各核素各反应道核数据不确定度导致的keff计算的不确定度.对比显示,两方法得到的不确定度量化结果符合很好.在多维正态分布空间内,对核数据进行抽样,代入输运程序得到keff计算值.统计分析表明,keff计算值很好地符合了正态分布,验证了在一般核数据的不确定度范围内keff与核数据近似成线性关系.这表明在一般的核数据不确定度范围内,基于线性模型的灵敏度法不确定度量化方法是可靠的.但对不确定度很大的核数据,灵敏度法不确定度量化的可靠性需进一步考察.对各核素各反应道截面,抽样法不确定度量化结果与灵敏度法结果均有很好的符合,验证了SURE程序抽样法模块的可靠性,在进一步检验后将应用于复杂非线性问题模拟计算的不确定度量化.为减少计算时间,将在抽样法的基础上发展多项式混沌展开方法用于复杂的多物理问题的灵敏度分析与不确定度量化.
[1]USDOE 2002 A Technology Roadmap for Generation-IV Nuclear Energy Systems USDOE/GIF-002-00(Washington:USDOE)p1
[2]Salvatores M,Jacqmin R 2008 Uncertainty and Target Accuracy Assessment for Innovative Systems Using Recent Covariance Data Evaluations NEA/WPEC-26(Paris:OECD/NEA)p1
[3]Marable J H,Weisbin C R 1979 Theory and Application of Sensitivity and Uncertainty Analysis(Oak Ridge:Oak Ridge National Laboratory)p16
[4]Gilli L,Lathouwers D,Kloosterman J L,van der Hagen T H J J 2013 Nucl.Sci.Eng.175 172
[5]Kim D H,Gil C S,Lee Y O 2008 International Conference on Nuclear Data for Science and Technology Nice,France,April 22–27,2007p289
[6]Kodeli I 2008 Sci.Technol.Nucl.Instll.2008 659861
[7]Pusa M 2012 Sci.Technol.Nucl.Instll.2012 157029
[8]Williams M L,Rearden B T 2008 Nucl.Data Sheets 109 5
[9]Hu Z H,Wang J,Sun W L,Li M S 2013 Atom.Energy Sci.Technol.47 25(in Chinese)[胡泽华,王佳,孙伟力,李茂生2013原子能科学技术47 25]
[10]Dossantos-Uzarralde P J,Guittet A 2008 Nucl.Data Sheets 109 2894
[11]Gilli L,Lathouwers D,Kloosterman J L,van der Hagen T H J J,Koning A J,Rochman D 2013 Ann.Nucl.Energy 56 71
[12]Williams M M R 2007 Nucl.Sci.Eng.155 109
[13]Wieselquist W,Zhu T,Vasiliev A,Ferroukhi H 2013 Sci.Technol.Nucl.Instll.2013 549793
[14]Zhu T,Vasiliev A,Ferroukhi H,Pautz A 2014 Nucl.Data Sheets 118 453
[15]Zhu T,Vasiliev A,Ferroukhi H,Pautz A 2015 Ann.Nucl.Energy 75 713
[16]Zhu T,Vasiliev A,Ferroukhi H,Pautz A,Tarantola S 2015 J.Nucl.Sci.Technol.52 8
[17]Chadwick M B,Herman M,Oblozinsky P 2011 Nucl.Data Sheets 112 110
[18]Engle W W J 1967 A User’s Manual for ANISN:A One-Dimensional Discrete Ordinates Transport Code with Anisotropic Scattering(Oak Ridge:Oak Ridge Gaseous Di ff usion Plant Computing Technology Center)p1
[19]Macfarlane R E,Muir D W,Boicourt R M,Kahler A C 2012 The NJOY Nuclear Data Processing System(Los Alamos:Los Alamos National Laboratory)p1
[20]Kiedrowski B C,Brown F B 2013 Nucl.Sci.Eng.174 227
[21]Briggs J B 2004 International Handbook of Evaluated Criticality Safety Benchmark Experiments(Paris:Nuclear Energy Agency)p1
PACS:28.20.—v,28.20.Gd,28.41.AkDOI:10.7498/aps.66.012801
*Project supported by the Key Laboratory of Neutron Physics of China Academy of Engineering Physics(Grant No.2013AA02),Sub-item of Special Project of the National Energy Bureau,China(Grant No.2015ZX06002008),National Magnetic Con fi nement Fusion Energy Research Project,China(Grant No.2015GB108002).
†Corresponding author.E-mail:hu_zehua@iapcm.ac.cn
Uncertainty quanti fi cation in the calculation of keffusing sensitity and stochastic sampling method∗
Hu Ze-Hua1)2)†Ye Tao1)2)Liu Xiong-Guo1)2)Wang Jia1)2)
1)(Institute of Applied Physics and Computational Mathematics,Beijing 100094,China)2)(Software Center for High Performance Numerical Simulation,China Academy of Engineering Physics,Beijing 100088,China)(Received 7 July 2016;revised manuscript received 30 September 2016)
The sensitivity and uncertainty analysis(S/U)method based on the fi rst order perturbation theory is commonly employed to calculate the uncertainties in-nuclear reactor’s integral parameters,such as the neutron e ff ective multiplication factor(keff),due to uncertainties in nuclear data.However,this method is only theoretically suitable for the linear model because of its fi rst order approximation.Moreover,S/U method is difficult to incorporate into a neutronics code,because the adjoint angular fl ux is needed to obtain the sensitivity coefficient of an integral parameter to nuclear data.Meanwhile,the sampling approach based on parametric random sampling of input parameters,an easy implemented method,evaluates the uncertainties in the integral parameters by performing a set of neutronics simulations inputted with a set of stochastic nuclear data sampled from a multinomial normal distribution with nuclear cross section mean values and covariance data.The sampling approach is considered as a more exact method,as linear approximation is not needed.With the increase of computational power,the sampling methods with consuming more time are now possible.The sampling approach is incorporated into SURE,a sensitivity and uncertainty analysis code developed in IAPCM,as a functional module.A careful veri fi cation of the new function is necessary before it is used to analyze complicated problems,such as multi-physical coupling calculations of nuclear reactor.Two simple fast criticality benchmark experiments,namely Godiva(HEU-MET-FAST-001)and Jezebel(PU-MET-FAST-001),are selected to verify the sampling module of SURE.The uncertainties in nuclear data are given by multigroup covariance matrices processed from ENDF/B-VII.1data.The uncertainties in the computed value of keffresulting from uncertainties in the nuclear data are calculated with both S/U and sampling methods.The uncertainties due to reaction cross sections for each nuclide in two benchmarks given by two methods with the multigroup covariance matrices are in good agreement.Since the S/U module of SURE code is veri fi ed extensively,the correctness of the sampling function of the code is con fi rmed as well.The distribution of the kefffrom the sampling approach obeys the normal distribution pretty well,which indicates that keffvaries linearly with the nuclear data under its uncertainty range,since the nuclear data used in calculations are assumed to be normal distribution in the sampling method.The results from the sampling method also support the S/U method with linear approximation as a suitable uncertainty quanti fi cation method for keffcalculation.
uncertainty quanti fi cation,stochastic sampling method,sensitivity,nuclear data
10.7498/aps.66.012801
∗中国物理研究院中子物理学重点实验室基金(批准号:2013AA02)、能源局06重大专项(批准号:2015ZX06002008)和国家磁约束
核聚变能研究专项(批准号:2015GB108002)资助的课题.
†通信作者.E-mail:hu_zehua@iapcm.ac.cn

