海面随机起伏对噪声场空间特性的影响规律∗

周建波1)2) 朴胜春1)2)† 刘亚琴1)2) 祝捍皓3)

1)(哈尔滨工程大学,水声技术重点实验室,哈尔滨 150001)2)(哈尔滨工程大学水声工程学院,哈尔滨 150001)3)(浙江海洋大学海洋科学与技术学院,舟山 316022)(2016年7月22日收到;2016年10月9日收到修改稿)

海面随机起伏对噪声场空间特性的影响规律∗

周建波1)2) 朴胜春1)2)† 刘亚琴1)2) 祝捍皓3)

1)(哈尔滨工程大学,水声技术重点实验室,哈尔滨 150001)2)(哈尔滨工程大学水声工程学院,哈尔滨 150001)3)(浙江海洋大学海洋科学与技术学院,舟山 316022)(2016年7月22日收到;2016年10月9日收到修改稿)

对于1kHz以上声波,海面起伏会对浅海声传播产生显著影响,现有的噪声预报模型在建模过程中基本没有考虑海面起伏的影响.针对这一问题,本文基于传输理论建立了随机起伏界面下噪声场垂直相关性和指向性模型,仿真分析了海面起伏对噪声强度、垂直相关性与指向性的影响.结果表明,对于表面噪声,海面随机起伏使声波能量从中间阶简正波向低阶和高阶简正波转移,而对噪声强度起主要贡献的一般是中间阶简正波,所以海面起伏使得噪声强度减弱;简正波之间能量的耦合导致垂直平面上不同掠射角方向上到达的声波响应发生变化,经由海面反射大掠射角到达的声波响应以及中小角度到达的声波响应变弱,而经由海底反射大掠射角到达的声波响应变强;海面随机起伏还会扰动各阶简正波相位,使不同阶简正波互相关性变弱,致使噪声场的空间相关性也变弱.

传输理论,随机起伏,环境噪声,空间特性

1引 言

海洋环境噪声是海洋背景场的主要特性之一,是海洋中任意地点、任何时刻都存在的声场,是水声学研究中的重要组成部分.传统的水声学对海洋环境噪声的研究多是为了降低或抑制海洋环境噪声对水下设备的干扰,提升水下设备的工作性能[1].从另一个角度考虑,海洋环境噪声是海洋中永恒存在的声场,包含了水体及海底海面等环境特性信息.所以,可以利用环境噪声的特性来推测海底声学参数[2,3]、海面上风速[4]、提取声场格林函数[5]等.利用海洋环境噪声研究海洋环境物理特性的优势在于环境噪声测量可以通过很小的代价获得较丰富的海洋声学信息,因此研究海洋环境噪声特性具有积极意义.

海洋环境噪声模型可为噪声场时空分布特性、空间相关性及指向性等提供数值预报.海洋环境噪声模型是在噪声源研究的基础上结合波导声传播特性发展起来的.Cron和Sherman[6]最早基于射线方法,给出了噪声场水平和垂直相关函数.该模型没有考虑海底的影响,而且没有考虑声线的折射效应,所以只适用于均匀的深海环境;在Cron和Sherman模型的基础上,Chapman[7]加入了海底反射的影响,导出了以俯仰角为变量的噪声强度和噪声垂直相关函数;Kuperman和Ingenito[8]利用波动理论处理噪声传播问题,同时考虑近场连续谱以及远场离散谱贡献,给出了水平分层介质中噪声场空间相关函数.Cary[9]将抛物方程传播模型和海面噪声源耦合起来,计算了水平非均匀波导环境下噪声场的垂直分布.但是该方法只适合远场,且只适合低频浅海噪声预报;Perkins和Kuperman[10]采用绝热简正波理论,给出了三维环境下噪声场的空间预报模型,但是该模型准确程度有待检验;Harrison[11]采用射线理论,给出了一种适合高频噪声场空间特性的预报模型,在一定程度上弥补了波动方法的局限;Yang和Kwang[12]利用近场快速场模型远场简正波模型建立了分层介质中噪声垂直指向性预报模型,该方法由于计算速度快、物理意义明确而被广泛应用;Buckingham等[13]研究了海底声速和衰减对噪声场的垂直指向性的影响,并用噪声垂直指向性来反演这些参数,并得到沉积层表层声速;Aredov和Furduev[14]通过噪声场的垂直指向性计算了海底反射损失,详细研究了海底反射系数与频率、掠射角的关系.国内学者在海洋环境噪声预报方面也做了大量的工作,黄益旺等[15,16]将体积噪声标量场模型和K-I噪声标量场模型扩展到矢量场,研究了噪声场中声压与质点振速3个正交分量的相关特性,推导得到了窄带噪声场空间相关系数的解析表达式;铁广鹏和郭新毅[17]结合实验数据提出了两种非高斯噪声模型以匹配实际的非平稳的海洋环境噪声,相对于传统的噪声模型,该模型适用范围更为广泛;林建恒和高天赋[18]采用简正波模型与射线模型相结合的方法来计算噪声的空间相关特性,在保证计算精度的同时提高了计算速度;孙军平等[19]分析了典型船舶水下辐射噪声实验数据,据以数值构建船舶辐射噪声,该研究对开展海洋信道船舶水下辐射噪声特性研究有重要意义和实际价值.He等[20]在已有的海面噪声模型的基础上,提出了航道附近海洋环境噪声预报模型,很好地解释了实验测量的噪声水平相关特性.以上学者为海洋环境噪声的完善和发展都做出了重要贡献.

海洋环境噪声源有很多,其中风生噪声是海洋环境噪声的重要组成部分,0.3—50kHz区间内海洋环境噪声和海洋表面状况及所观察区域的风有直接的关系,也就是说这个频段范围的海洋环境噪声主要是由风和海面相互作用产生的.海面在风的扰动下必然会随机起伏,关于起伏界面引起的声散射问题早在20世纪70年代就有学者开展了相关研究[21−23],但是都存在着计算速度慢或者计算精度低等问题.Thorsos等[24,25]近几年基于传输理论给出了一种新的起伏界面下声散射预报模型,并研究了海面起伏对声传播的影响.他们的研究结果表明,对于几百赫兹的声波,在绝大部分常见的海况下,海面的随机起伏对声传播影响比较弱,可以不予考虑.对于1kHz以上的声波,界面起伏对声传播有显著的影响,尤其是对于浅海,随机起伏界面对声传播的影响不能被忽略.Colosi和Morozov[26],Kaustubha和John[27]对传输理论模型做了进一步完善,将声速起伏和界面起伏声场预报模型统一起来,细致地分析了声速起伏和界面起伏对模态之间的能量耦合、相位的扰动以及声场干涉结构的影响,再次证明了海面起伏对中高频段的声传播的影响不容忽略,而噪声场的特性是由噪声源特性及其传播特性共同决定的,所以浅海高频海洋环境噪声特性必然也会受海面起伏的影响.然而现有的噪声预报模型在处理声传播过程时都将海面当作平整界面处理,没有考虑海面随机起伏的影响.针对这一问题,本文基于传输理论方法,给出各向同性P-M波浪谱下噪声场垂直相关性和指向性模型,仿真分析海面起伏对噪声场空间特性的影响,并对仿真结果从物理机制方面进行了解释.

2随机起伏界面下的噪声预报模型

2.1 传输理论模型

由简正波理论可知,水平分层介质中简谐点源的声场可以表示成一系列简正波的叠加:

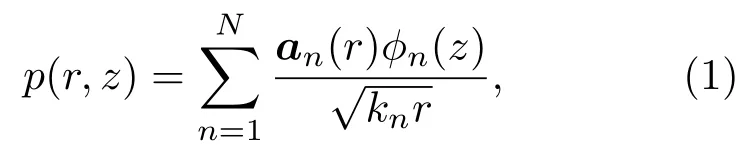
其中an(r)为模态幅度函数,r为接收点距离声源的水平距离,ϕn(z)为海面没有起伏时声场实本征函数,kn为声场本征值的实部,N为简正波的阶数.当海面平整时,an(r)由声源深度决定,而当海面是随机起伏的,an(r)由声源深度和海面起伏剧烈程度共同决定.实际的海洋波导中海水海底介质都是存在吸收的,所以声场本征值一般为复数,设声场本征值ln=kn+iαn,其中αn可以通过微扰法获得.

Creamer[28]给出了浅海海面随机起伏条件下模态幅度函数an(r)随距离的演化方程:

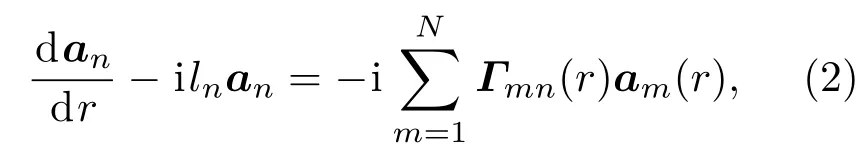
其中Γmn为海面波浪起伏作用下模态耦合矩阵.当海面起伏较小时,大部分能量作为相干波沿着镜反射方向传播,小部分能量作为非相干波被散射到其他方向.需要指出的是(2)式中的an(r)是相干波模态幅度与非相干波模态幅度之和.忽略二维界面散射效应,利用一阶微扰理论,模态耦合矩阵可以用下式表示[22]:

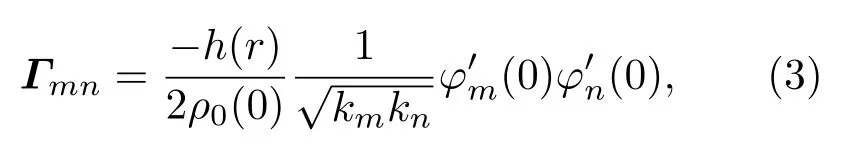
其中h(r)为海面位移,ρ0(0)为海面处海水密度,为海面处第m阶模态本征函数的导数.这里我们关心的是声场的二阶统计量〈p(r,z1)p∗(r,z2)〉:

该微分方程为非刚性微分方程,可以利用Adams-Bashfourth-Moulton算法求解.其中Imp,qn为散射矩阵,表达式为[25]

式中kqp=kp−kq,Δmn,qp(ξ)= 〈Γmn(r)Γqp(r+ξ)〉为第m阶和n阶模态耦合矩阵与第p阶和q阶模态耦合矩阵的水平相关函数.

这里我们选择P-M波浪谱进行研究,P-M波浪谱Sh(k)表达形式如下[25]:

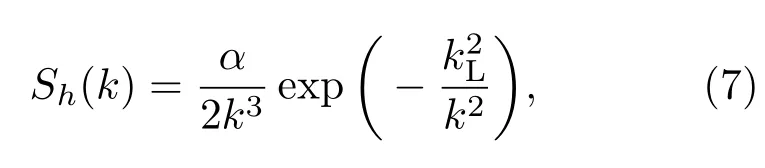
其中α =8.1× 10−3,kL= βg2/U4,β =0.74,g=9.81m/s2,U为海面上方19.5m高度上的风速.利用(7)式生成随机起伏海面位移h(r),然后代入到(3)式和(6)式中,便可得到粗糙海面散射矩阵:

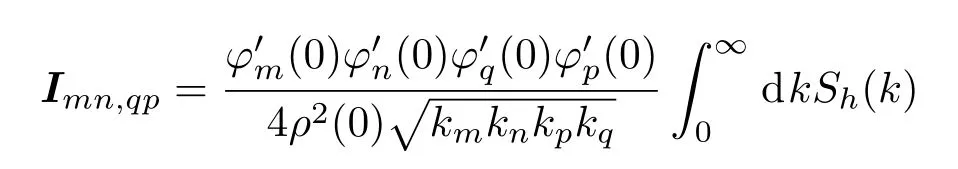
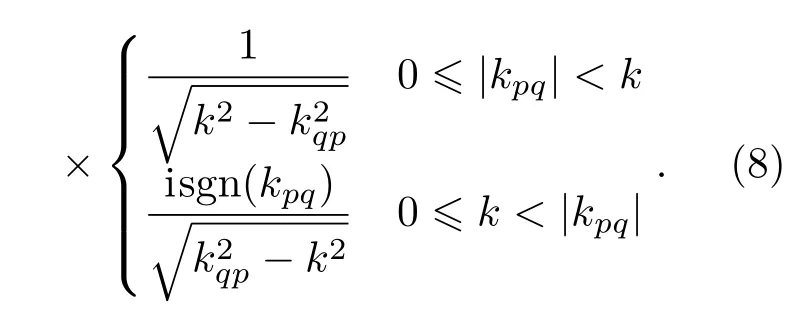
对(8)式中积分部分进行三角代换并化简可以得到:

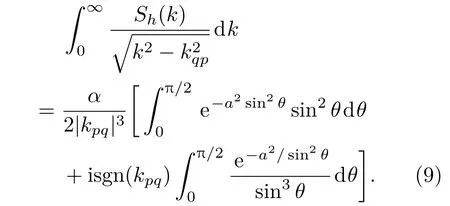
将(9)式代入到(8)式中,通过数值积分可得到散射矩阵,代入到(5)式中即可求解得到模态相关矩阵

2.2 噪声场垂直相关性模型

假设统计互不相关的噪声源均匀分布在海面下方某一深度的无限大平面上.对于任意一小的噪声面元ds,该面元内噪声源作用下垂直方向上声场的互谱密度dC12可以表示成:

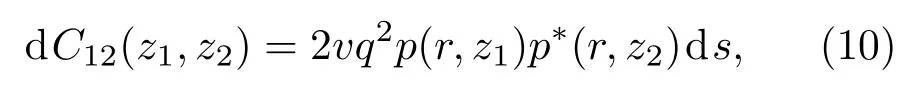
其中v为单位面积噪声源密度,q为噪声源强度.假设海面粗糙度在水平方向是各向同性的,且海洋环境与水平方位角无关,那么半径为Rnoise的圆区域范围内噪声源作用下噪声场的互谱密度为

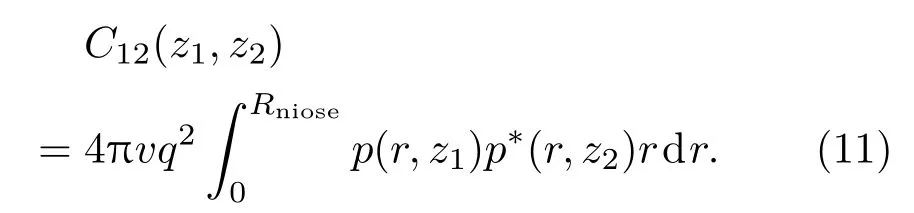
将(4)式代入到(11)式中,便可得到垂直方向上空间两点声场的互谱密度:

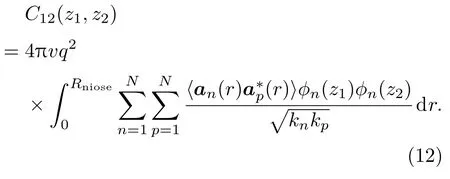
当z1=z2,(12)式表示的是z1点的噪声强度;当z1=z2,将(12)式做归一化处理可得不同深度z1和z2上的两点垂直相关性.

2.3 噪声场垂直指向性模型

考虑不相关噪声源,对于给定的掠射角θ,结合垂直阵列波束形成,可以得到θ方向上到达的声波响应B(θ)为[12]

其中kc为声波波数,zt为第t个接收器深度.假设噪声源强度均匀,且海洋环境为水平分层,上式可以写成:

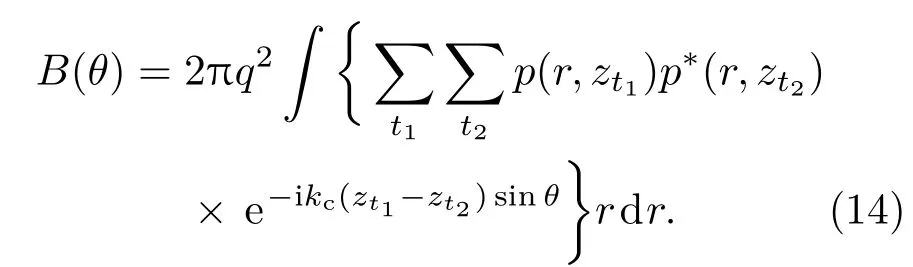
将(4)式代入到(14)式即可得到噪声场的垂直指向性:

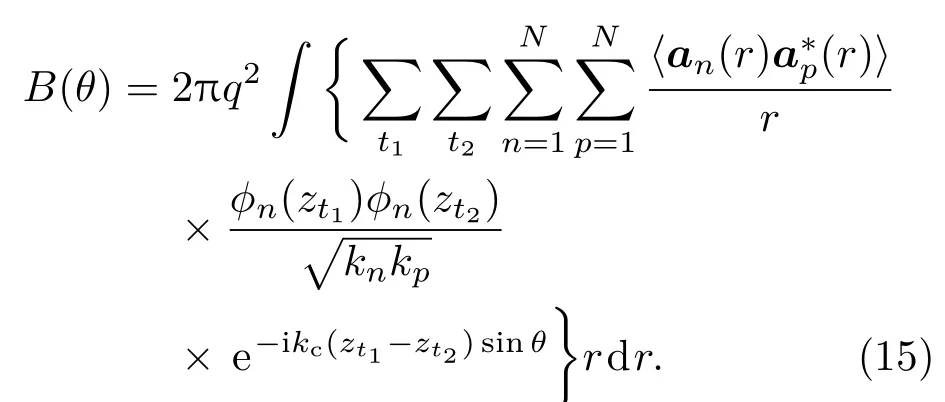
通常,简正波模型被认为是一种远场近似模型,近场范围内得到的声场是不准确的,所以现有的基于简正波方法的噪声垂直指向性模型都将近场和远场分开考虑,远场声场采用简正波方法,而近场声场则用射线或者快速场方法.Westeood等[29]给出了一种基于参考深度的简正波模型,该模型在近场范围也能给出精确的解.这里我们选择用Westwood等给出的简正波模型来求解本征函数和本征值,所以直接用(15)式即可得到噪声场垂直指向性,无需对近场远场分开考虑.

3仿真计算

3.1 海面随机起伏对声传播的影响

为了更好地理解起伏海面对噪声场空间特性的影响.这里先仿真研究起伏界面对声传播的影响.仿真的海洋环境如图1所示,海深H=40m,海水声速、密度和衰减分别为cw=1500m/s,ρw=1.0g/cm3,αw=0.000063dB/λ. 海底为液态半无限空间,海底声速、密度和衰减分别为cb=1623m/s,ρb=1.77g/cm3,αb=0.2dB/λ,仿真的声波频率1000 Hz,海面风速为5.5m/s.

图1 海洋环境示意图Fig.1.Schematic of waveguide in which simulations are performed.

为了突出海面起伏对声传播的影响,这里先忽略海水以及海底吸收的影响.此时,能量传输方程满足:

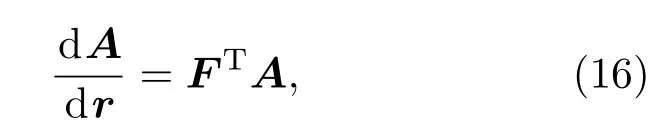
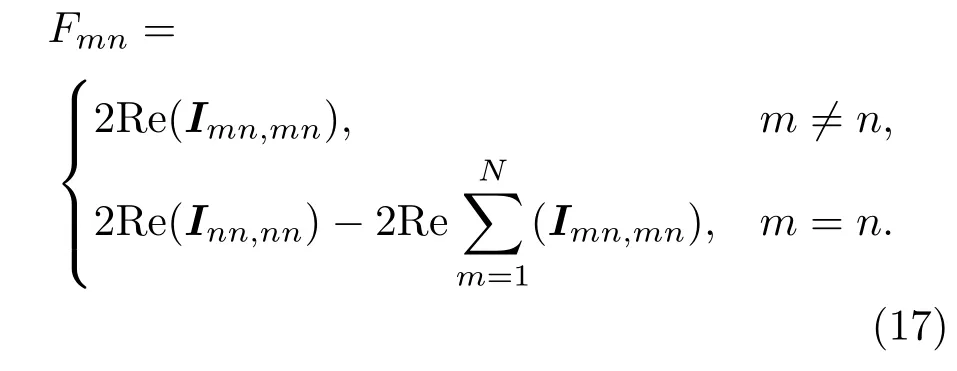
(16)式的解可以写成:A(r)=V exp(−λr)VTA0,其中λ =diag[λ1···λn]和V=[v1···vn]分别为矩阵FT的特征值和特征向量,A0代表的是各阶模态能量初始值.这里我们关注矩阵F的特征值,因为它的大小决定模态初始能量A0随着距离指数衰减的速度.由于这里忽略了所有衰减的影响,所以λn的大小决定了第n阶模态耦合的能量衰减速度.为第n阶模态耦合距离.由简正波理论可知,海水和海底吸收引起的能量衰减速度是由本征值虚部决定的,模态能量衰减距离定义为Pn=[2αn]−1.

图2给出的是各阶模态的耦合距离和衰减距离,随着模态阶数增加,模态的衰减距离减小,也即越高阶模态传播距离越短,而低阶模态因为出射角度较小,受海底衰减影响较小,所以可以远距离传播.模态耦合距离则随着阶数增加逐渐减小.当Rn＜Pn时,表示该阶模态能量在能量被衰减完之前可以发生能量耦合.从图2中可以看到第二阶以及更高阶的模态都可以发生能量耦合,而第一阶模态基本不受海面起伏的影响.图3给出的是Fmn,其物理意义是第m阶模态和第n阶模态的耦合强度.从图3中可以看到,模态之间耦合满足对称性,高阶模态之间的耦合一般要大于低阶模态之间的耦合,且阶数相差较小的简正波之间耦合和能量转移能力一般要强于阶数相差较大的情况.

图2 模态耦合距离和衰减距离Fig.2.Mode coupling range and attenuation range.

图4给出的是风速为0和5.5m/s(传输理论方法和Monte Carlo方法)时声压传播损失,选取的声源深度zs=10m,接收深度zr=20m.从图中可以看到,本文所用的传输理论模型和Monte Carlo模型得到的结果基本符合,验证了传输理论模型的有效性.此外,海面有无起伏对声压传播损失曲线产生了显著差异,说明海面起伏对高频声传播具有显著影响.因此在计算高频声传播时,海面起伏的影响应该予以考虑.

图3 (网刊彩色)模态耦合强度Fig.3.(color online)Strength of mode coupling.

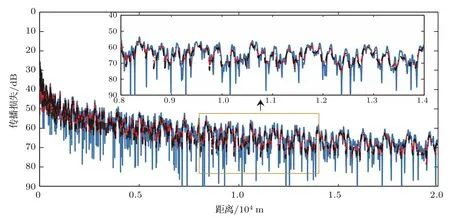
图4 (网刊彩色)声压传播损失,风速0m/s(蓝色实线)、风速5.5m/s传输理论方法(红色点线)、风速5.5m/s Monte Carlo方法(黑色点划线)Fig.4.(color online)Pressure propagation loss,for wind speed 0m/s(blue solid line),transport theory with wind speed 5.5m/s(read dot line),and Monte Carlo simulation with wind speed 5.5m/s(black dot dash line).

3.2 海面随机起伏对噪声强度的影响

由文献[16]可知,海面起伏最直接的影响就是会导致声波能量损耗,这里首先研究海面起伏对噪声强度的影响.图5给出的是风速为0,5.5和10.0m/s时1000 Hz的噪声强度,由于选取的噪声源强度为单位值,所以给出的噪声强度为相对强度.当风速为零时,海面没有起伏,此时噪声强度最大.随着风速增加,海面起伏加剧,在全海深范围内噪声强度都有所减弱,尤其在海面和海底附近,噪声强度的衰减尤为明显.由文献[12]可知,整个界面噪声源作用下第n阶噪声模态的强度

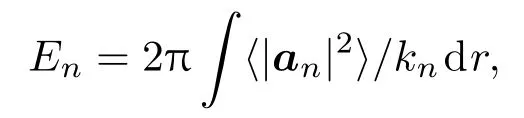
那么当海面没有起伏和有起伏时,第n阶噪声模态能量强度差值

其中〈|anf|2〉和〈|anr|2〉分别为海面没有起伏和有起伏时第n阶噪声模态的能量.若Dn＞0,表示海面随机起伏使得该阶模态向外转移能量,对噪声场强度的贡献减弱;反之则表明海面随机起伏使得该阶模态获得能量,该阶模态对噪声场强度贡献增强.图7给出的是海面没有起伏时20km范围内噪声源作用下各阶噪声模态强度En.由于噪声源比较浅,低阶简正波模态激发强度很弱,虽然这部分模态能量衰减较小,但并不是对声场起主要贡献的,高阶模态出射角较大,受海底衰减影响比较严重,作用距离非常有限,所以对噪声强度起主要贡献的主要是中间部分模态.图8给出了海面没有起伏和有起伏时各阶噪声模态强度差值,对于低阶模态和高阶模态,Dn＜0;而对于中间模态,Dn＞0.也就意味海面起伏会使中间模态能量向高阶以及低阶模态转移,但是低阶模态耦合获得的能量非常少,高阶模态获得能量后受海底衰减影响比较严重,能量迅速衰减,所以海面起伏导致噪声强度的减弱.

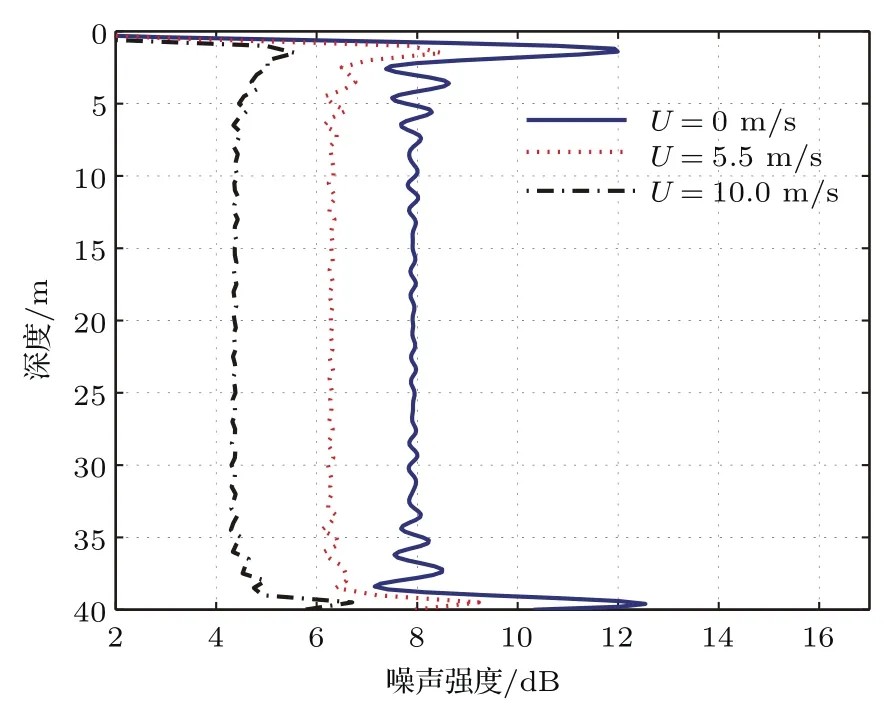
图5 (网刊彩色)不同风速下噪声强度Fig.5.(color online)Noise intensity for di ff erent wind speed.

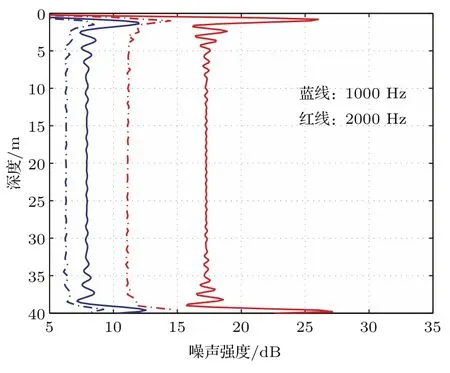
图6 (网刊彩色)不同频率下噪声强度Fig.6. (color online)Noise intensity for di ff erent frequencies.

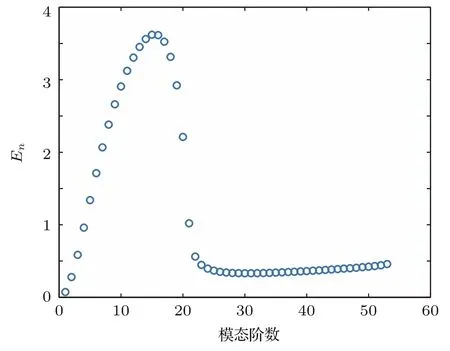
图7 海面无起伏噪声模态能量Fig.7.The noise modal intensity for unperturbed surface.

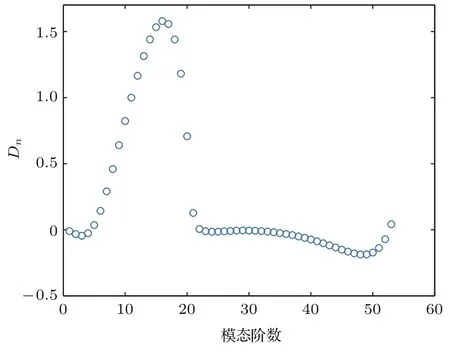
图8 海面无起伏和有起伏噪声模态能量差Fig.8.The di ff erence of noise modal intensity between unperturbed and perturbed case.

图6给出的是1000 Hz(蓝线)和2000 Hz(红线)在不同风速(实线U =0m/s,点线U =5.5m/s)下的噪声强度仿真结果.显然海面起伏对高频噪声强度影响更加明显.相同海面起伏使得1000 Hz噪声强度衰减约1.5dB,而使2000 Hz噪声强度衰减达到约5dB.可见,相同海面起伏下,声波频率越高,能量损耗越严重.这一结论对精确估计风生噪声源强度是很有必要的.现有的噪声源强度估计模型基本都没有考虑海面起伏对声传播过程的影响,所以现有预报模型得到的中高频噪声源强度可能偏小.

3.3 海面随机起伏对噪声场相关性的影响

海面起伏不仅会引起各阶简正波模态能量的变化,还会扰动各阶模态的相位,所以,海面起伏不但会影响噪声强度,还会对声场的空间相关性产生影响.图9给出了风速为0,5.5和8.0m/s时1000 Hz的噪声垂直相关性.如果不考虑海水以及海底的吸收,当海面没有起伏时,任意两阶模态随着距离有确定的相位差关系.而当海面存在随机起伏,各阶模态相位会被起伏的海面随机延迟或者提前,所以造成了不同阶模态相关性降低,最终导致场的相关性也变弱.图11和图12分别给出的是风速为0和8.0m/s时不同模态归一化相关函数((a)是1和2,2和3以及3和4阶模态归一化相关系数,(b)是10和11,11和12以及12和13阶模态归一化相关系数,(c)是20和21,21和22以及22和23阶模态归一化相关系数).模态归一化相关函数定义为其中n和p代表模态阶数.低阶模态受海面起伏影响较小,所以相关性下降的比较缓慢,而高阶模态受海面起伏影响比较大,所以各阶模态相关性迅速下降.对比两种风速下的模态相关系数,可以看到:海面起伏越大,不同模态间的相关性衰减越迅速,尤其是高阶模态相关性受海面起伏剧烈程度的影响尤为明显.因此海面起伏加剧,噪声场的相关性衰减更快.

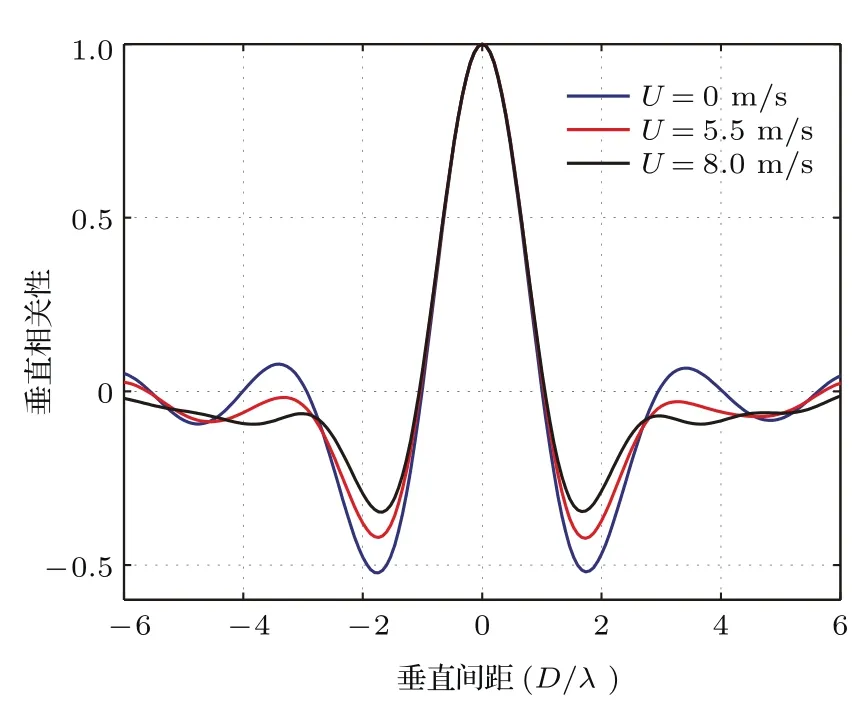
图9 (网刊彩色)不同风速下垂直相关Fig.9.(color online)Vertical spatial correlation for di ff erent wind speed.

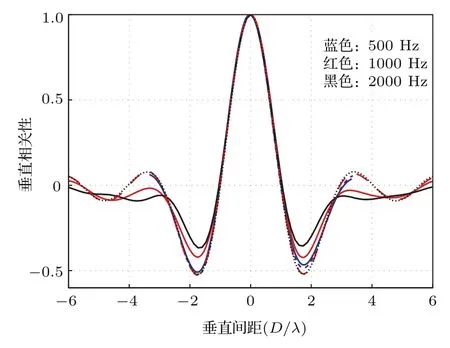
图10 (网刊彩色)不同频率和风速下垂直相关Fig.10.(color online)Vertical spatial correlation for di ff erent frequencies and di ff erent wind speed.

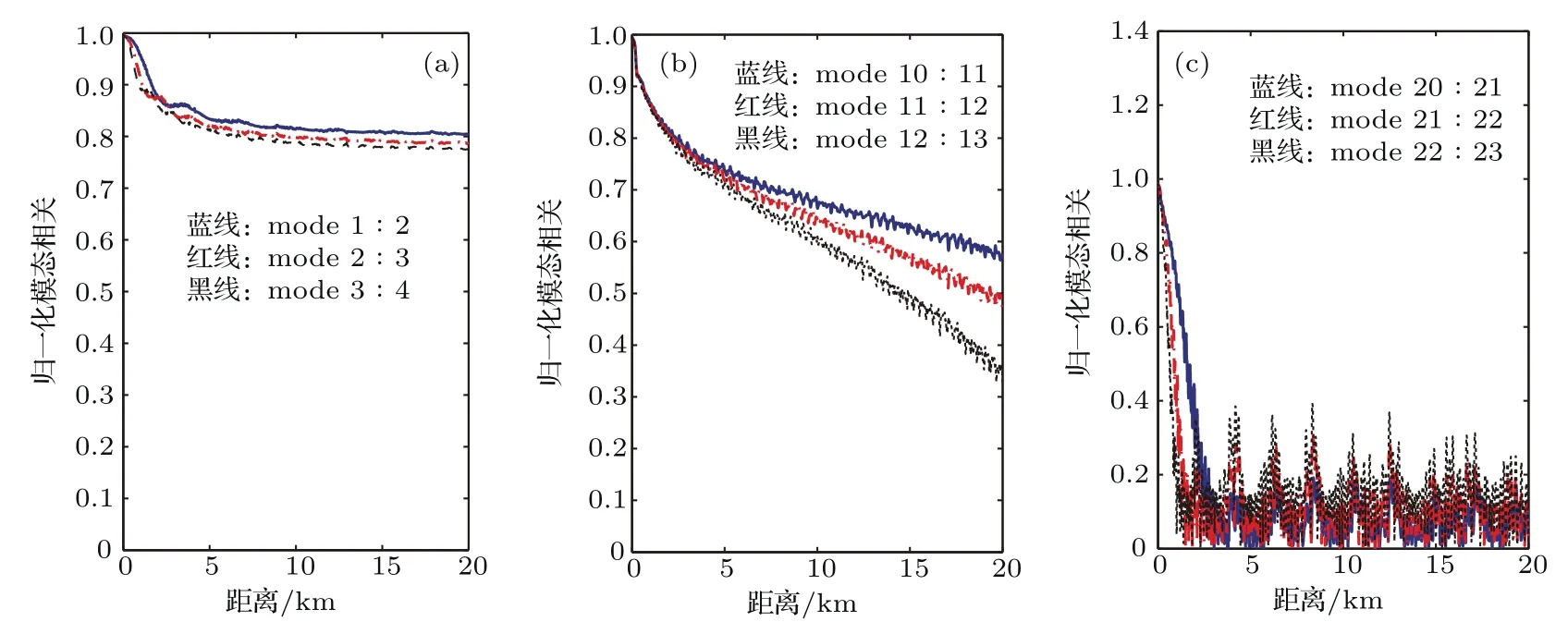
图11 (网刊彩色)U=5.5m/s模态归一化相关函数Fig.11.(color online)Normalized mode coherences for the case with U=5.5m/s.

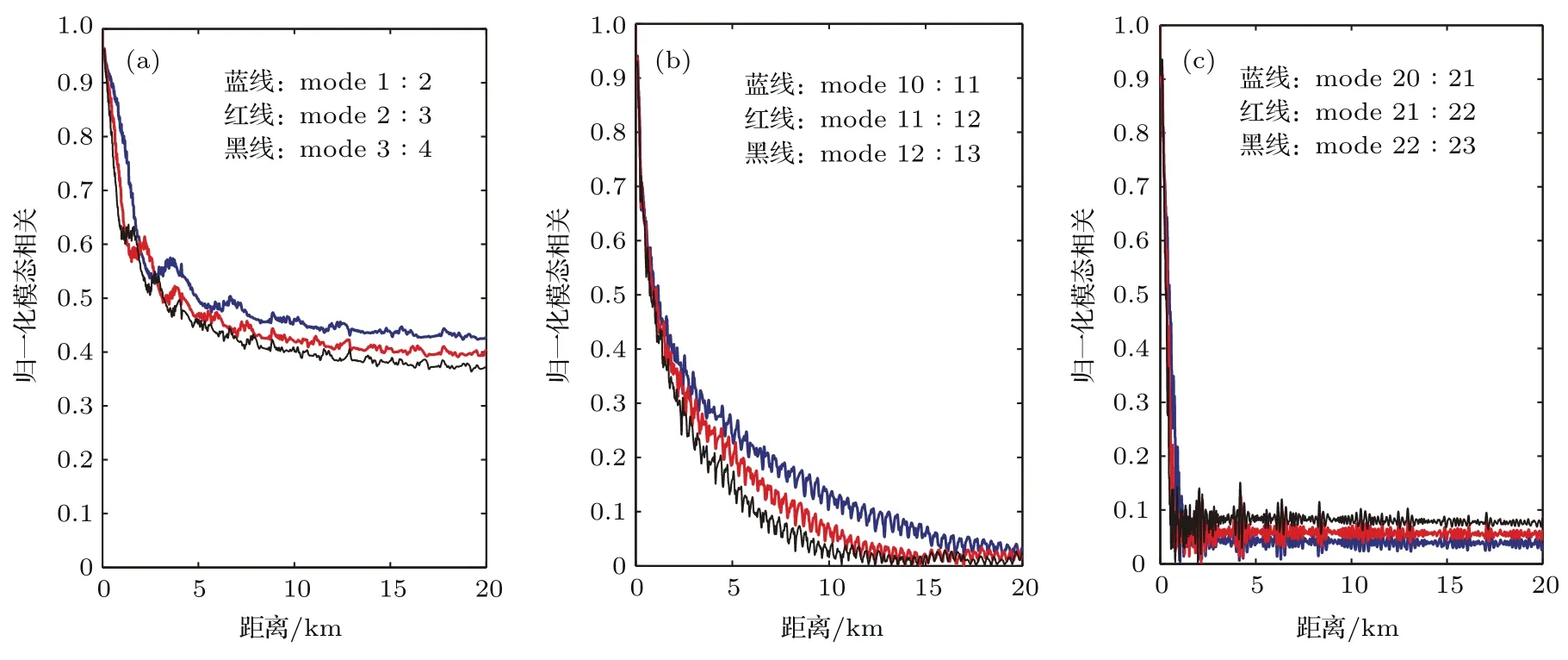
图12 (网刊彩色)U=8.0m/s模态归一化相关函数Fig.12.(color online)Normalized mode coherences for the case with U=8.0m/s.

图10给出的是500,1000和2000 Hz三个频率下不同风速时的噪声场垂直相关性.其中虚线对应的是风速为0m/s时的结果,而实线对应风速为5.5m/s时的结果.当海面没有起伏时,仿真条件下噪声场的垂直相关性基本和频率无关,仅依赖于垂直间距和声波波长的比值.而当海面存在起伏时,不同频率声波受海面起伏影响程度不同,所以此时噪声场垂直相关性不仅仅依赖于垂直间距,还和频率有关.这是海面有起伏和没有起伏时中高频噪声场空间特性的一个显著差异.

3.4 海面随机起伏对噪声场垂直指向性的影响

噪声场垂直指向性描述的是垂直平面上不同掠射角到达的声波响应强度.当界面存在起伏时,各阶简正波能量发生耦合,某些模态能量增强,某些模态能量减弱,能量增强的模态对应掠射角到达的声波响应会增加,能量减弱的模态对应掠射角度到达的声波响应就会减弱.这里,我们结合起伏界面下各阶模态能量耦合来分析界面起伏对噪声场垂直指向性的影响.

为了验证本文所用噪声垂直指向性模型的正确性,图13给出了两种方法得到的海面没有起伏时500 Hz噪声场垂直指向性,其中蓝线和红线分别是用快速场方法和本文所用的方法得到的结果.快速场方法在近场范围内也能给出比较准确的声场解,所以快速场方法得到的指向性结果是考虑了“头顶”噪声源作用的结果.从图中可以看到两种方法的结果在小掠射角范围内基本上完全符合,只有在大掠射角范围内才有微小的差异,噪声场在垂直方向上的响应最大差异约17.3dB,而两种模型误差不超过0.4dB,显然这个差异完全在可接受范围内.证明了本文所选用的噪声垂直指向性模型是可信的.

图13 (网刊彩色)噪声场垂直响应Fig.13.(color online)The noise vertical directionality.

图14 (网刊彩色)海面有无起伏噪声场垂直响应Fig.14.(color online)The noise vertical directionality for unperturbed and perturbed case.

图15 (网刊彩色)海面无起伏和海面有起伏时各阶模态能量对比Fig.15.(color online)The mode energies for the unperturbed and perturbed case.

图14给出了1000 Hz噪声场垂直指向性.其中蓝线和红线分别是海面风速为0和5.5m/s时不同掠射角上到达的声波响应.正角度响应对应的是直达声线、海面反射声线和海底-海面反射声线,而负角度响应则对应的是海底反射声线.在小掠射角|θ|＜5°范围内,海面起伏对这个角度范围内到达的声波响应基本没有影响;在5°＜ |θ|＜ 25°范围内,海面没有起伏时这个掠射角范围到达的声波响应要强于海面有起伏时的声波响应;对于更大掠射角,从海面反射到达的声波强度变弱,而从海底反射到达声波强度变强.图15给出的是U=0m/s和U=5.5m/s时部分模态能量〈|an|2〉,其中实线对应的是U=0m/s时的结果,点划线对应的是U=5.5m/s时的结果.海面起伏对第一阶模态能量影响非常小.定义rmin,n为起伏海面第n阶模态获取能量对应的最大水平距离,在r＜rmin范围内,模态主要是从其他阶模态获得能量,超过这个距离后模态主要是向其他阶模态输出能量.在0—20km范围内,海面有起伏时前三阶模态能量总大于海面没有起伏时这几阶模态能量.海面起伏对这几阶模态做正功,这几阶模态获得的能量大于它们向外转移的能量(见图15(a)).因为声源靠近海面,低阶模态激发强度很弱,由于耦合而获得的能量也非常少,所以低号阶模态虽然整体上获得能量,但是这部分模态对应掠射角到达的声波响应增强得并不明显.随着模态阶数的增加,rmin越来越小,在绝大部分距离上,海面有起伏时模态能量曲线斜率大于海面没有起伏时能量曲线斜率(见图15(b)),也即这部分能量大幅度向其他阶模态转移.随着模态阶数继续增加,模态在整个传播距离上都向外输出能量,而不获取能量(见图15(c)),海面起伏导致这些模态获得的能量小于它们向外转移的能量,所以这部分模态对应的掠射角达到的声波响应要小于海面没有起伏时这部分模态的响应.结合图8可以看到,第16阶模态向外转移的能量最多,相应地,这阶模态对应掠射角θ=17°声波响应变弱得最为明显.而对于第22阶附近的模态,海面起伏基本不改变其模态能量,所以这阶模态对应掠射角方向上到达的声波响应基本没有变化.由文献[22]可知,当海面粗糙起伏时,海面不再是绝对反射边界,声波每次和海面作用后都会损耗能量,尤其是对于大掠射角入射的声波,能量损耗尤为严重,所以海面有起伏时经由海面反射到达的声波强度会变弱.而海面起伏使得高阶模态获得的能量大于其向外转移的能量,所以从海底方向以大掠射角到达的声波响应变强.

4结 论

本文基于传输理论模型建立了随机起伏界面下风生噪声场空间相关性模型和指向性模型.仿真分析了海面随机起伏对声传播、噪声强度、噪声垂直相关性和指向性的影响.仿真结果表明,海面随机起伏能够使得简正波模态之间发生能量耦合,高阶模态间耦合作用要强于低阶模态间能量耦合.对于风成表面噪声,海面起伏使得中间阶模态损失能量,而低阶模态和高阶模态获得能量,而对噪声强度起主要贡献的恰恰是中间阶模态,所以海面起伏使得噪声强度减弱.中间阶模态向外转移的能量大于获得的能量,因此这部分模态对应掠射角到达的声波响应会变弱.海面有起伏时,声波和海面作用后会发生能量损耗,所以经由海面反射大掠射角到达的声波强度变弱,而高阶模态获得的能量大于向外转移的能量,所以经由海底反射大掠射角到达的声波强度变强.海面起伏不仅影响各阶模态幅度,还会扰动各阶模态相位,降低模态之间相关性,最终导致噪声场相关性越弱.本文所给出的模型可以考虑海面起伏对高频声传播的影响,这对准确估计高频噪声源强度有积极意义.此外,大掠射角范围内噪声垂直响应受海面起伏影响比较明显,所以必然包含了海面风速、起伏等气象信息,所以可以考虑用来进行海面参数反演等工作.

[1]Guo X Y,Li F,Tie G P 2014 Physics 43 723(in Chinese)[郭新毅,李凡,铁广鹏 2014物理43 723]

[2]Buckingham M J,Jones S A 1987 J.Acoust.Soc.Am.81 938

[3]Harrison C H,Simons D G 2002 J.Acoust.Soc.Am.112 1377

[4]Lin J H,Chang D Q,Ma L,Li X J,Jiang G J 2001 Acta Acust.26 217(in Chinese)[林建恒,常道庆,马力,李学军,蒋国建2001声学学报26 217]

[5]Arnaud D,Eric L,Mickael T 2003 J.Acoust.Soc.Am.113 2973

[6]Cron B F,Sherman C H 1962 J.Acoust.Soc.Am.34 1732

[7]Chapman D M 1989 J.Acoust.Soc.Am.85 648

[8]Kuperman W A,Ingenito F J 1980 J.Acoust.Soc.Am.67 1988

[9]Carey W M 1986 J.Acoust.Soc.Am.80 1523

[10]Perkins J S,Kuperman W A 1993 J.Acoust.Soc.Am.93 739

[11]Harrison C H J 1997 J.Acoust.Soc.Am.102 2655

[12]Yang T C,Kwang Y 1997 J.Acoust.Soc.Am.101 2541[13]Buckingham M J,Deane G B,Carbone N M 1995 J.Comput.Acoust.10 101

[14]Aredov A A,Furduev A V 1994 J.Acoust.Phys.40 176

[15]Huang Y W,Yang S E,Piao S C 2009 J.Harbin Engineer.Univ.1 1209(in Chinese)[黄益旺,杨士莪,朴胜春2009哈尔滨工程大学学报1 1209]

[16]Huang Y W,Yang S E 2010 J.Harbin Engineer.Univ.2 137(in Chinese)[黄益旺,杨士莪2010哈尔滨工程大学学报2 137]

[17]Tie G P,Guo X Y 2014 Tech.Acous.33 209(in Chinese)[铁广鹏,郭新毅 2014声学技术 33 209]

[18]Lin J H,Gao T F 2003 Tech.Acous.22 119(in Chinese)[林建恒,高天赋 2003声学技术 22 119]

[19]Sun J P,Yang J,Lin J H,Jiang G J,Yi X J,Jiang P F 2016 Acta Phys.Sin.65 124301(in Chinese)[孙军平,杨军,林建恒,蒋国健,衣雪娟,江鹏飞 2016物理学报 65 124301]

[20]He L,Li Z L,Zhang R H,Peng Z H 2008 Chin.Phys.Lett.25 582

[21]Guy V N,Jorge C N 1994 J.Acoust.Soc.Am.99 2013

[22]Kuperman W A,Ingenito F 1977 J.Acoust.Soc.Am.61 1178

[23]Rouse ffD,Ewart T E 1995 J.Acoust.Soc.Am.98 3397

[24]Thorsos E I,Elam F S,Hefner W T,Reynolds B T,Stephen A R,Yang J 2010 Second International Shallow-Water Conference ShangHai,China,September 16–20,2009p99

[25]Thorsos E I,Henyey F S,Elam W T,Reynolds S A,Williams K L 2004 High Frequency Ocean Acoustics California,America,March 1–5,2004p132

[26]Colosi J A,Morozov A K 2009 J.Acoust.Soc.Am.126 1026

[27]Kaustubha R,John A C 2015 J.Acoust.Soc.Am.137 2950

[28]Creamer D B 1996 J.Acoust.Soc.Am.99 2825

[29]Westwood E K,Tindle C T,Chapman N R 1996 J.Acoust.Soc.Am.100 3631

PACS:43.20.+g,43.30.+m,02.30.Gp,02.30.HqDOI:10.7498/aps.66.014301

*Projectsupported by theScienceand Technology Foundation ofStateKey Laboratory,China (GrantNo.9140C200103120C2001),the National Natural Science Foundation of China(Grant No.11234002),and the Open Foundation from Fishery Sciences in the First-class Subjects of Zhejiang,China(Grant No.20160004).

†Corresponding author.E-mail:piaoshengchun@hrbeu.edu.cn

Ocean surface wave e ff ect on the spatial characteristics of ambient noise∗

Zhou Jian-Bo1)2)Piao Sheng-Chun1)2)†Liu Ya-Qin1)2)Zhu Han-Hao3)

1)(Acoustic Science and Technology Laboratory,Harbin Engineering University,Harbin 150001,China)2)(College of Underwater Acoustic Engineering,Harbin Engineering University,Harbin 150001,China)3)(Marine Science and Technology College,Zhejiang Ocean University,Zhoushan 316022,China)(Received 22 July 2016;revised manuscript received 9 October 2016)

The ocean ambient noise fi eld experiences a stochastic process of many such noise sources and the respective interactions of their wave fi elds with the waveguide boundaries.At frequencies of about 1kHz and higher,forward scattering from surface wave can strongly a ff ect shallow water sound propagation.However,most of the available ambient forecasting models do not consider the e ff ects of multiple forward scattering from surface wave.Therefore,there is a need for an accurate method of predicting ambient noises at middle and high-frequency which can account for surface scatterings.Aiming at such a requirement,a propagation model based on transport theory method is described which yields the second-order moment of the acoustic fi eld.Monte Carlo simulations of acoustic propagation loss are employed to validate the transport theory method.The mode number dependence of mode coupling phenomenon is demonstrated at 1000 Hz via the competing e ff ects of mode coupling and attenuation ranges.Low and middle propagating modes are seen to have a smaller coupling range than the attenuation range,allowing mode coupling e ff ects to take precedence over attenuation e ff ects.The mode energies and the coherences are also examined,and it is found that the mode coupling rate for surface wave is signi fi cant,but strongly dependent on mode number.Mode phase randomization by surface waves is found to be dominated by coupling e ff ects.On the basis of transport theory propagation model,connecting with the properties of ambient noise sources,a spatial characteristic model for ambient noise under surface wave is presented.Further,the e ff ects of surface wave on ambient noise intensity,vertical correlation and vertical directionality are analyzed.Simulation results show that the surface wave may result in energy transfer from medium modes to low modes and high modes,the rate of energy transfer depends on the mode energy di ff erence.Since the medium mode plays an important role in noise intensity,the noise intensity decreases with the increase of surface wave.In addition to noise intensity,the vertical correlation of ambient noise also decreases due to mode phase randomization by surface wave.Besides,mode coupling can also lead to a change of vertical beam intensity distribution,positive high-angle beams associated with direct,surface,and bottom-surface-bounced rays become weaker,while negative high-angle beams associated with bottom bounced rays become stronger.Since the vertical directionality is sensitive to surface wave,the model can be applied to ocean surface parameter inversion.In summary,the model provided in this paper is closer to actual ocean waveguide and has future prospect in ocean acoustic engineering application.

transport theory,random fl uctuation,ambient noise,spatial characteristics

10.7498/aps.66.014301

∗国防科技重点实验室基金(批准号:9140C200103120C2001)、国家自然科学基金重点项目(批准号:11234002)和水产浙江省一流学科开放课题(批准号:20160004)资助的课题.

†通信作者.E-mail:piaoshengchun@hrbeu.edu.cn