响应曲面法在CTD烘梗丝工艺参数优化中的应用

赵静芬，李坚，李日南，邹克兴，张旭升，朱静

（广西中烟工业有限责任公司技术中心，广西南宁530001）

响应曲面法在CTD烘梗丝工艺参数优化中的应用

赵静芬，李坚，李日南，邹克兴，张旭升，朱静

（广西中烟工业有限责任公司技术中心，广西南宁530001）

在单因素试验的基础上，利用响应曲面法的中心复合表面设计，对CTD烘梗丝工艺参数进行优化分析。选择PG温度、PG流量、PG含氧量作为优化因素，研究各因素的不同水平对烘梗丝出口含水率均值的影响；选择HT蒸汽流量、物料流量作为优化因素，研究各因素的不同水平对烘梗丝出口含水率标准偏差的影响。通过响应曲面分析得到烘梗丝的最优条件为PG温度200℃，PG流量21 500 m3/h，PG含氧量2.21%，HT蒸汽流量391.6 m3/h，物料流量3 428 kg/h；在此条件下，烘后梗丝含水率CPK值可达到1.21。

响应曲面法；CTD；梗丝；优化

含水率是烟草制丝加工工艺中的重要检测和控制参数之一，特别是关键加工工序——加料和烘丝等重要工艺点，必须对烟丝（梗丝）含水率进行严格控制才能保证烟丝（梗丝）的加工品质。南宁卷烟厂制梗丝生产线采用意大利COMAS公司的CTD气流干燥设备进行梗丝膨胀烘干，该设备在使用过程中存在烘后梗丝含水率波动较大的问题，表现为含水率CPK值[1]偏低，一般在0.7～0.9，明显低于生产过程其他工艺点的控制水平，不符合工厂精益生产的要求。

响应曲面分析法（Response surface methodology，RSM）是一种优化工艺条件的有效方法，可检查响应变量与一系列试验变量之间的关系，确定试验因素及其交互作用在工艺过程中对指标响应值的影响，精确地表述因素和响应值之间的关系[2-4]。将响应曲面分析法应用于烘梗丝工艺的研究中，更有利于表述和研究各因素对含水率CPK值的影响，为提高烘梗丝出口含水率的控制稳定性、提升梗丝品质提供准确的试验数据。

1 材料与方法

1.1 材料和仪器

材料：一类烤烟型卷烟叶组所用的配方梗丝，广西中烟南宁卷烟厂提供。

仪器：CTD型烘梗丝机，意大利COMAS公司产品；TM710e型在线红外水分仪，NDC红外技术公司产品。

1.2 试验方法

利用单因素方差分析、等方差检验等分析方法分别找出影响烘后梗丝含水率均值和标准偏差的烘梗丝工艺参数，然后针对含水率均值和标准偏差分别利用响应曲面法设计试验进行工艺参数优化。

式中：M——工艺标准规定的中心值；

T——2倍允差；X——数据的平均值；σ——数据的标准偏差。

1.3 针对含水率均值的响应面优化试验设计

中心复合表面设计（CCF）因素水平见表1。

表1 中心复合表面设计（CCF）因素水平

应用Minitab软件，采用中心复合表面设计方法，在前期单因素试验的基础上，对影响烘梗丝出口含水率均值的主要工艺条件进行试验设计，同时进行局部控制，使其他非关键因素保持一致。

1.4 针对含水率标准偏差的响应面优化试验设计

试验因素与水平设计见表2。

表2 试验因素与水平设计

应用Minitab软件，采用中心复合表面设计方法，在前期单因素试验的基础上，对影响烘梗丝出口含水率标准偏差的主要工艺条件进行设计，同时进行局部控制，使其他非关键因素保持一致。

2 结果与分析

2.1 含水率均值的试验结果分析

2.1.1 模型的拟合

响应曲面CCF设计及试验结果见表3。

表3 响应曲面CCF设计及试验结果

中心复合表面设计二次模型方差分析见表4。

表4 中心复合表面设计二次模型方差分析

由表4可看出，回归F值为9.25，多元相关系数R2=89.28，预测R2=59.53，调整R2=79.62，说明模型对试验实际情况拟合较好；p=0.001（p＜0.05视为模型拟合显著），表明该模型高度显著，可用来进行响应值的预测，试验设计方案正确。

二次模型回归方程系数显著性检验见表5。

表5 二次模型回归方程系数显著性检验

由表5表明，因素A对含水率均值的线性效应极显著，因素B，C对含水率均值的线性效应显著；因素B2，C2对含水率均值的曲面效应极显著，因素A2对含水率均值的曲面效应不显著；因素AB，AC，BC对含水率均值的交互影响不显著。说明3个因素均不同程度地对响应值产生显著或极显著的影响，试验设计的因素选择是成功的。

将未达到显著水平的因素剔除，将其平方和及自由度并入剩余项，进行第2次方差分析，以提高检验的精确度。

第2次方差分析见表6

表6 第2次方差分析

第2次方差分析，回归F值为14.25，多元相关系数R2=83.58，预测R2=61.72，调整R2=77.71，说明模型对试验实际情况拟合较好；p＜0.000 1，表明该模型高度显著，可用来进行响应值的预测。根据模型失拟性分析p=0.278＞0.05，说明该模型无失拟。

第2次回归方程系数显著性检验见表7。

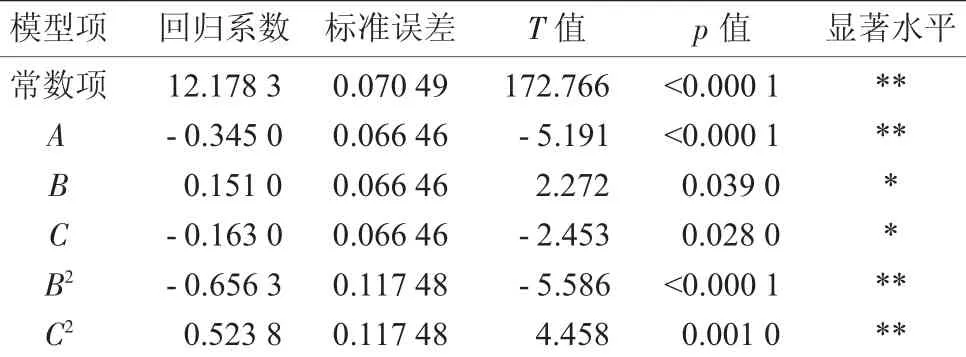
表7 第2次回归方程系数显著性检验

由表7分析表明，模型回归及保留的各因素项均达到显著水平，说明含水率均值与试验因素之间存在极显著的回归关系，其优化的回归方程为：

Y=12.178 3-0.345A+0.151B-0.163C-

0.656 3B2+0.523 8C2.

2.1.2 响应曲面图与等值线图的分析

通过响应曲面图与等值线图对任意2个因素对含水率均值的交互影响进行分析与评价，以确定最佳因素水平范围。

PG流量和PG含氧量对CTD出口含水率均值交互影响的等值线图（a）和曲面图（b）见图1。

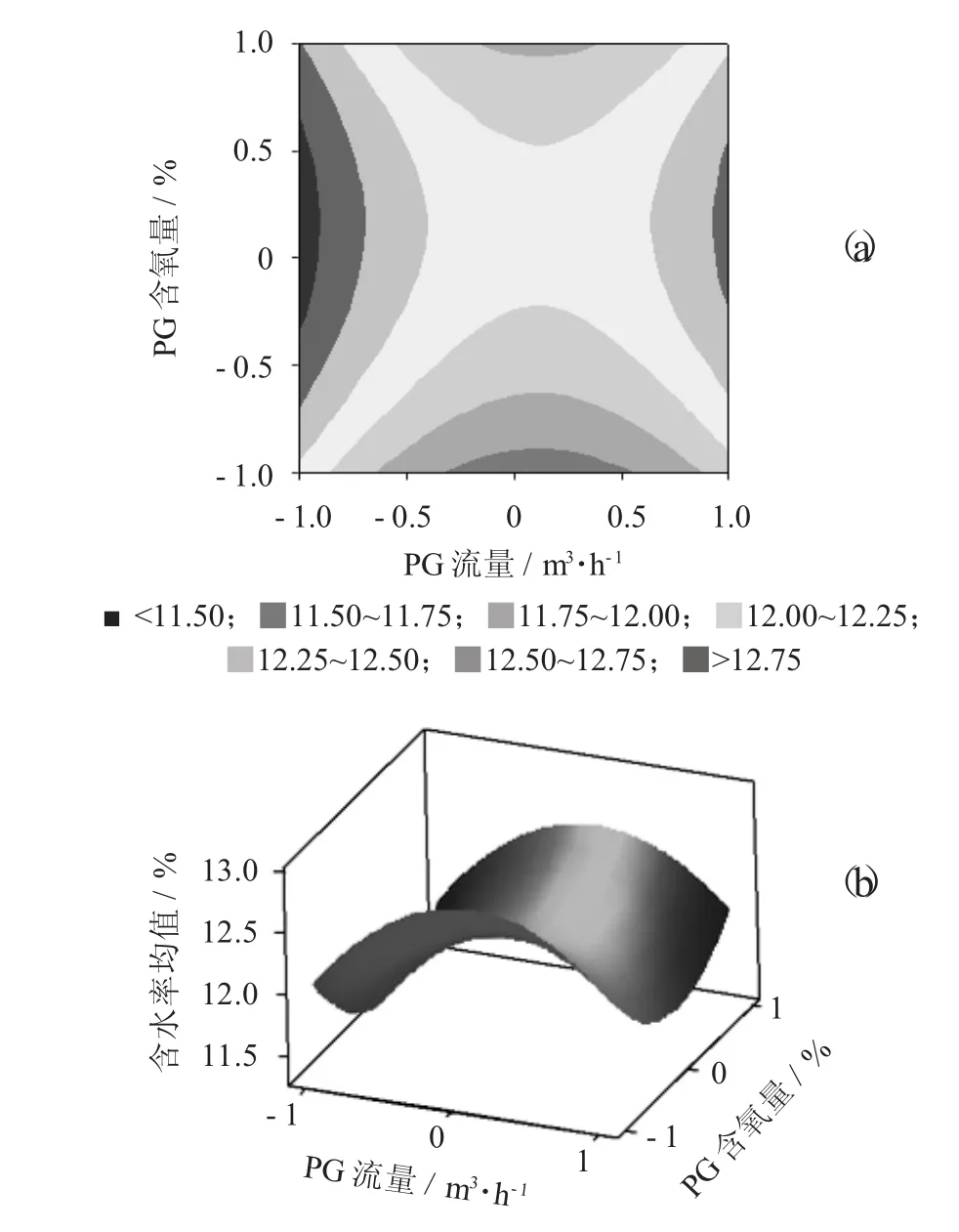
图1PG流量和PG含氧量对CTD出口含水率均值交互影响的等值线图（a）和曲面图（b）

图1 显示了PG温度为220℃时，PG流量和PG含氧量对CTD出口含水率均值的交互影响。在PG流量不变的条件下，随着PG含氧量的增加，含水率均值出现先降低后升高的趋势。在PG含氧量不变的条件下，随着PG流量的增加，含水率均值先升高后降低。

PG温度和PG含氧量对CTD出口含水率均值交互影响的等值线图（a）和曲面图（b）见图2。

图2PG温度和PG含氧量对CTD出口含水率均值交互影响的等值线图（a）和曲面图（b）

图2 显示了PG流量为22 000 m3/h时，PG温度和PG含氧量对CTD出口含水率均值的交互影响。在PG温度不变的条件下，随着PG含氧量的逐渐增加，含水率均值出现先降低后升高的趋势。在PG含氧量不变的条件下，随着PG温度的升高，含水率均值出现降低的趋势。

PG温度和PG流量对CTD出口含水率均值交互影响的等值线图（a）和曲面图（b）见图3。

图3显示了PG含氧量为2.5%时，PG温度和PG流量对CTD出口含水率均值的交互影响。在PG温度不变的条件下，随着PG流量的逐渐增加，含水率均值出现先升高后降低的趋势。在PG流量不变的条件下，随着PG温度的升高，含水率均值出现降低的趋势。

使用响应优化器直接计算最优解。

含水率均值试验的响应优化器计算结果见图4。

由图4可知，当PG温度200℃，PG含氧量2.21%，PG流量21 500 m3/h时，含水率均值可达到12.0%。在此基础上进行试验验证，实测含水率均值为12.02%。

2.2 含水率标准偏差的试验结果分析

2.2.1 模型的拟合

图3 PG温度和PG流量对CTD出口含水率均值交互影响的等值线图（a）和曲面图（b）

图4 含水率均值试验的响应优化器计算结果

试验设计及结果见表8，二次模型方差分析见表9。

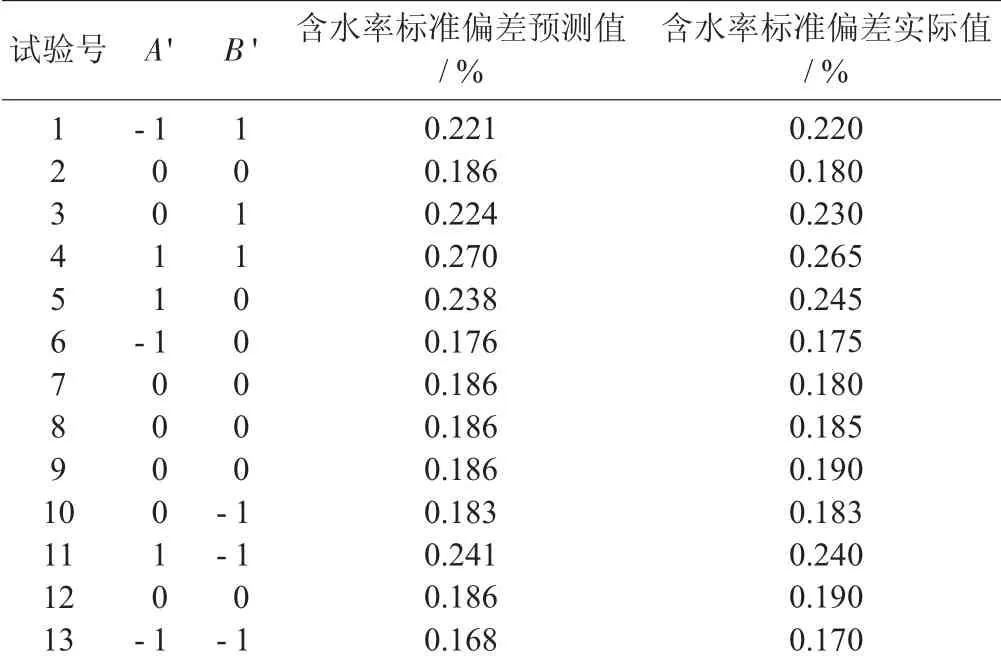
表8 试验设计及结果

表9 二次模型方差分析

由表9可以看出，回归F值为73.57，多元相关系数R2=98.13，预测R2=89.44，调整R2=96.80，说明模型对试验实际情况拟合较好；p＜0.000 1（p＜0.05视为模型拟合显著），表明该模型高度显著，可用来进行响应值的预测，试验设计方案正确。

二次模型回归系数显著性检验见表10。

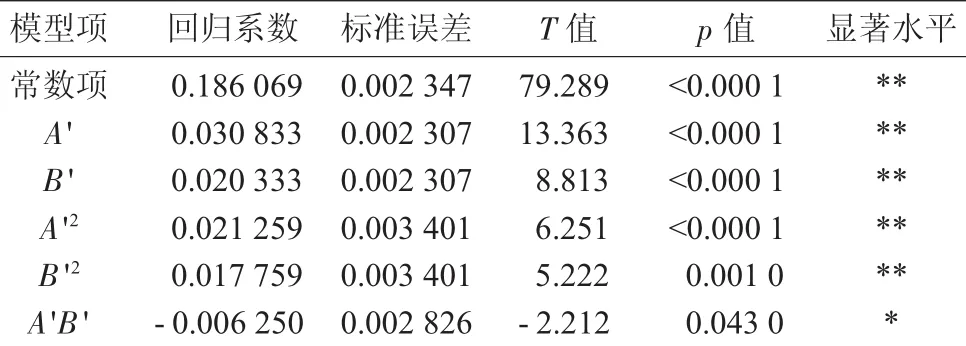
表10 二次模型回归系数显著性检验

由表10分析表明，模型回归的各因素项均达到显著水平，说明含水率标准偏差与试验因素之间存在极显著的回归关系，其回归方程为：

Y'=0.186 069+0.030 833A'+0.020 333B'+

0.021 259A'2+0.017 759B'2-0.006 25A'B'.

2.2.2 响应曲面图与等值线图的分析

物料流量和HT蒸汽流量对CTD出口含水率标准偏差交互影响的等值线图（a）和曲面图（b）见图5。

图5 物料流量和HT蒸汽流量对CTD出口含水率标准偏差交互影响的等值线图（a）和曲面图（b）

由图5可以看出，确实存在1个区域可以使含水率标准偏差达到最小。

由Minitab软件得到优化条件的处理，确定最优工艺条件为HT蒸汽流量391.6 m3/h，物料流量3 428 kg/h，理论计算CTD出口含水率标准偏差达到0.156%。在此基础上进行试验验证，实测含水率标准偏差为0.158%。

结合烘梗丝出口含水率均值的数据，计算可得CPK值为1.21。

3 结论

通过响应曲面试验设计方法，分别考查了PG温度、PG流量、PG含氧量对CTD烘梗丝出口含水率均值的影响，以及HT蒸汽流量、物料流量对CTD烘梗丝出口含水率标准偏差的影响。二次方程的模

型回归极显著，且失拟性检验不显著，说明通过本试验所建立的二次回归方程成功地反映了所考查各因素与响应值之间的相关性，试验设计科学合理。CTD烘梗丝的最佳工艺条件为PG温度200℃，PG流量21 500 m3/h，PG含氧量2.21%，HT蒸汽流量391.6 m3/h，物料流量3 428 kg/h；在此条件下，烘后梗丝含水率CPK值为1.21。

[1]李卫红.质量统计技术[M].北京：中国计量出版社，2006：45-82.

[2]马林，何桢.六西格玛管理[M].北京：中国人民大学出版社，2003：359-365.

[3]陈魁.试验设计与分析[M].北京：清华大学出版社，1996：94-180.

[4]马逢时.六西格玛管理统计指南——MINITAB使用指导[M].北京：中国人民大学出版社，2011：475-488.◇

第6期（总第433期）农产品加工No.6 2017年6月Farm Products ProcessingJun.

Response Surface Methodology as an Approach for Optimization of CTD Drying Process of Cut Stem

ZHAO Jingfen，LI Jian，LI Ri'nan，ZOU Kexing，ZHANG Xusheng，ZHU Jing
（Technology Center，Guangxi Tobacco Industry Limited Liability Company，Nanning，Guangxi 530001，China）

Response surface methodology（RSM）based on a central composite face-centered design（CCF）is applied for the optimization of CTD drying process of cut stem.In RSM analysis，the pairwise interactive effects of PG temperature，PG flow，oxygen level，on the yield of the mean and the HT steam flow，inlet cut stem flowon the yield of the standard deviation of outlet moisture are examined.Results show that the optimal values of the above parameters are determined as follows：PG temperature 200℃，PG flow 21 500 m3/h，oxygen level 2.21%，HT steam flow 391.6 m3/h and inlet cut stem flow 3 428 kg/h.Under the optimized conditions，the experimental CPK value of outlet moisture is 1.21.

response surface methodology；CTD；cut stem；optimization

TS412

A

10.16693/j.cnki.1671-9646（X）.2017.06.008

1671-9646（2017）06a-0028-05

文章编号：1671-9646（2017）06a-0024-04

2017-05-09

赵静芬（1985—），女，硕士，工程师，研究方向为烟草加工工艺技术。

超声波辅助燕麦多酚提取