基于时差的导弹协同定位技术
陈书恒,唐 极,易凤琼
(1.海军装备研究院,上海 200436;2.解放军92492部队,海南 三亚 572528;3.解放军75706部队,广东 广州 510500)
基于时差的导弹协同定位技术
陈书恒1,唐 极2,易凤琼3
(1.海军装备研究院,上海 200436;2.解放军92492部队,海南 三亚 572528;3.解放军75706部队,广东 广州 510500)
导弹协同作战的关键技术之一就是导弹协同定位技术。针对多导弹时差定位系统,建立了定位模型,推导了定位误差表达式并作了仿真分析,针对不同布站形式对定位精度变化趋势进行了阐述。
协同作战;时差;定位
0 引 言
导弹协同作战的关键技术之一就是导弹协同定位技术,目前导弹中制导阶段主要依靠导弹自身的惯导/全球定位系统(GPS)组合定位,但战时我方卫星若遭到敌方打击,如何对敌方的雷达目标进行精确定位也成为一个棘手的难题[1]。采用导弹协同定位是解决问题的途径之一,为了使导弹获得很好的隐蔽性、更远的作用距离、更大的覆盖范围,定位应采用无源定位。
目前无源定位方法主要包括测向交叉法、时差定位法等[2]。多站时差定位具有定位精度高、速度快、抗干扰能力强等特点[3],本文主要在不同布站形式、确定的站址误差以及授时误差情况下对定位精度变化趋势进行分析。
1 多站时差定位算法
在三维空间中,辐射源信号到达2个观测站的时间差可以确定以2个观测站为焦点的双曲面。一般情况下,三维定位需要4个观测站同时接收辐射源信号,得到3组互不相关的时差,从而规定目标所在的3个双曲面,其交点就是目标位置[4]。换言之,在空间中至少需要4枚导弹同时接收辐射信号才能对空间目标定位[5]。
设空间时差定位系统由1个主子弹O0(x0,y0,z0)和3个副子弹O1(x1,y1,z1)、O2(x2,y2,z2)和O3(x3,y3,z3)构成,辐射源为T(x,y,z),如图1所示。通过比较信号到达4个子弹的到达时间(TA),即可测量得到3个时差TDOA:
TDOAi=TAi-TA0=Δti,i=1,2,3
(1)
定义距离:
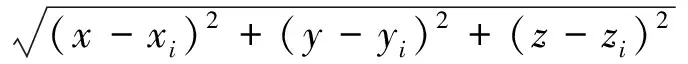
i=0,1,2,3
(2)
因此上述时差测量实质为距离差:
(3)
式中:c为电磁波的传播速度。
将距离公式(2)代入式(3)进行移项并平方后,整理可得:
(x0-xi)x+(y0-yi)y+(z0-zi)z=ki+r0·Δri
(4)
为求解式(4)所确定的非线性方程组,可先将r0看作1个已知量,从而得到如下表达式:
AX=F
(5)
当3个副站在x、y、z这3个方向均不等值时,A可逆,并且有:
(6)
令A-1=[aij]x×3,由式(6)可计算得到辐射源坐标:
(7)
(8)
将式(7)代入式(2)中r0的表达式,得到:
(9)
其中:
(10)
通过式(9)求解r0,即可得到辐射源位置。
2 算法仿真分析
本文对四站时差定位算法进行仿真分析,由于各站的分布情形对时差定位精度具有较大影响,仿真分析了不同布站形式、确定的站址误差和授时精度情况下的定位精度变化趋势,在不同的布阵形式下,定位精度变化趋势不同,因此在实际情况下应合理地选择布阵形式,以提高定位精度。
对于四站时差定位算法,仿真条件为:导弹间基线长度为50 km,目标距离导弹1 600 km,站址误差为100 m,授时精度为30 ns。具体仿真情形为:
(1) T形分布:假设在地心坐标系中O1、O2、O3坐标分别为(50,0,6 620)、(-50,0,6 620)、(0,0,6 620),O4在平面内以O1为圆心作圆周运动。在整个动态变化过程中,可以得到当O4的坐标为(15.2,0,6 667.6)时定位误差为最小值16.400 1 km,几何精度因子(GDOP)分布图如图2所示。
(2) Y形分布:假设在地心坐标系中O2、O3坐标分别为(0,43.3,6 620)、(0,-43.3,6 620),O1、O4在平面内以(0,0,6 620)为圆心作圆周运动。在整个动态变化过程中,可以得到当O1、O4的坐标分别为(8,0,6 647.7)、(24,0,6 691.1)时定位误差为最小值15.45 km,GDOP分布图如图3所示。
(3) 菱形分布:假设在地心坐标系中O2、O3坐标分别为(43.3,0,6 620)、(-43.3,0,6 620),O1、O4在平面内以(0,0,6 620)为圆心作圆周运动。在整个动态变化过程中,可以得到当O1、O4的坐标分别为(-22.8,0,6 630.3)、(22.8,0,6 609.7)时定位误差为最小值18.09 km,GDOP分布图如图4所示。
3 结束语
多导弹协同作战是未来战争的必然需求,利用时差技术对目标进行精确定位,可以提高打击精度。本文针对空间中多导弹时差定位进行了建模,并对定位误差进行了仿真分析,从仿真的结果看,在四弹时差定位的模型中,每种布阵形式定位精度的动态变化过程都不同。比如T形布阵形式虽没有最小的定位误差,但是在整个动态过程中的定位精度最为平滑,这使得在整个作战过程中,导弹编队的姿态更易控制。本文为多导弹协同作战提供了一种测向定位的方法,另外还需突破小型化技术、高精数字化接收测量技术、复杂电磁环境信号分选识别等技术,多导弹协同才能真正应用到实战中。
[1] FOY W H.Position-location solutions by Taylor-series estimation[J].IEEE Transactions on Aerospace and Electronic Systems,1976,12(2):187-194.
[2] 郭福成,樊昀.双星 TDOA/FDOA 无源定位方法分析[J].航天电子对抗,2006,22(6):20-23.
[3] 孙仲康,周一宇,何黎星.单多基地有源无源定位技术[M].北京:国防工业出版社,1996.
[4] 钟丹星,邓新蒲,周一宇.一种基于WGS-84地球面模型的卫星测时差定位算法[J].宇航学报,2003,24(6):569-573.
[5] 刘钰,陈红林.一种空间测向定位的解析算法和误差仿真分析[J].微处理机,2007(6):94-96.
MissileCooperationLocationTechnologyBasedonTimeDifference
CHEN Shu-heng1,TANG Ji2,YI Feng-qiong3
(1.Naval Academy of Armament,Shanghai 200436,China; 2.Unit 92492 of PLA,Sanya 572528,China;3.Unit 75706 of PLA,Guangzhou 510500,China)
One of key technologies for missile cooperation operation is missile cooperation location technology.Aiming at multi-missile time difference location system,this paper sets up location model,deduces the expression of location error and performs simulation analysis.Aiming at different station distribution types,the change trend of location precision is expatiated.
cooperation operation;time difference;location
2016-04-20
TN971
:A
:CN32-1413(2017)03-0026-03
10.16426/j.cnki.jcdzdk.2017.03.006

