基于短时傅里叶变换的噪声移频类灵巧干扰特征提取
宫 健,张 磊,陈 晨,熊 武
(1.西安电子科技大学,陕西 西安 710071;2.空军工程大学,陕西 西安 710051;3.解放军66133部队,北京 100043;4.解放军93792部队,河北 廊坊 065000;5.解放军94907部队,江西 南昌 330013)
基于短时傅里叶变换的噪声移频类灵巧干扰特征提取
宫 健1,2,张 磊3,陈 晨4,熊 武5
(1.西安电子科技大学,陕西 西安 710071;2.空军工程大学,陕西 西安 710051;3.解放军66133部队,北京 100043;4.解放军93792部队,河北 廊坊 065000;5.解放军94907部队,江西 南昌 330013)
灵巧干扰兼备压制干扰和欺骗干扰的特点,其主要的技术指标为干扰的瞬时变化性和随机生成性,傅里叶变换作为常用的信号处理工具只适用于确定信号和平稳信号,并不能对灵巧干扰进行有效分析,针对这一问题采用短时傅里叶变换来提取出噪声移频类灵巧干扰的特征,仿真了信号参数对干扰效果的影响,得出了有利于新型综合电子干扰系统研制和对抗的一些结论。
灵巧干扰;时频分析;噪声移频;短时傅里叶变换
0 引 言
雷达系统的电子干扰与反干扰技术在高技术军事战争中发挥着越来越重要的作用,各种新技术也随之迅猛发展[1-3]。灵巧干扰正是在各种先进的雷达技术普遍应用、传统的压制性干扰和欺骗性干扰不再能有效发挥作用的背景下提出的。
灵巧干扰作为一种新型干扰,兼备压制性和欺骗性双重优势,通常是用在雷达工作频率范围发射多个在时间上与真实回波信号重叠,并且遮盖住回波噪声的猝发式脉冲的方式实现[4-6]。
灵巧干扰的主要技术指标为干扰信号的瞬时变化性和随机生成性,傅里叶变换作为常用的信号处理工具,只适用于确定信号和平稳信号,并不能对灵巧干扰进行有效分析,因此本文研究了时频分析的基本工具——短时傅里叶变换来提取出噪声移频类灵巧干扰特征的方法。
1 雷达回波匹配滤波处理模型
1.1 线性调频信号
假设脉冲压缩雷达发射的波形为线性调频信号,表示为:
(1)
式中:T为脉冲宽度;μ=B/T为调频斜率;B为调频带宽。
对应匹配滤波器的频率响应为:
H(f)=kS*(f)exp(-j2πft0)
(2)
式中:k为匹配滤波器增益;t0为匹配滤波器的固有物理延迟。
为了数学分析的方便,可假设t0=0。滤波器的相频特性与回波信号的相频特性相反,即:
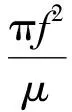
(3)
线性调频信号经匹配滤波器输出频谱为:
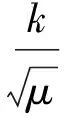
(4)
1.2 二相编码信号
二相编码脉冲信号的复数表达式为:
s(t)=u(t)exp(j2πf0t)
(5)
(6)
式中:u(t)为回波复包络;τ为子脉冲的时长;N为子脉冲的个数;T为整个编码的脉冲时长;φ(t)∈{φn=0,π},表示采用的相位调制函数;f0为工作频率。

(7)
式中:χ1(td,0)为子脉冲的自相关函数,并且:
(8)
χ2(mτ,0)是归一化伪随机序列的非周期自相关函数。
2 噪声移频类灵巧干扰时频分析模型
2.1 噪声移频类灵巧干扰
假设噪声移频函数为:
(9)
式中:n(t)为噪声信号;KFM为移频系数。
则噪声移频类灵巧干扰表示为:

(10)
由上式可见,噪声移频类灵巧干扰本质上是雷达信号与噪声调频信号的乘积,即:
(11)

(12)
经推导可得最小均方误差的系数an应为:

(13)
最小均方误差为:
(14)
则式(10)可分解为:
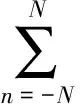
(15)
可见,噪声移频类灵巧干扰本质上可以看作2N+1个频移量为nΔf固定移频干扰的加权叠加。
2.2 短时傅里叶分析方法
1977年Allen给出了短时傅里叶变换(STFT)的定义[8]:

(16)
可见,z(t′)的短时傅里叶变换可以看作是z(t′)乘上1个以时间t为中心的“分析窗”γ*(t′-t)的傅里叶变换。
利用上面的原理对线性调频信号与二相编码信号通过匹配滤波器前后进行时频特性的仿真,结果如图1、图2所示。
3 噪声移频类灵巧干扰特征提取
3.1 线性调频信号噪声移频灵巧干扰仿真
下面对线性调频信号噪声移频灵巧干扰的时频域联合分布仿真,假设信号的时宽T=50 μs,频带宽度B=5 MHz,工作频率f0=10 MHz,用50 MHz频率进行采样,采用高斯白噪声移频调制,干扰增益10 dB,结果如图3所示。
由图3可见噪声移频类灵巧干扰使回波信号出现了密集的假目标,假目标出现的位置与移频量fd解得的时间是对应的。另外,也可以发现干扰峰值比回波峰值要低一些。所以移频调制对线性调频信号的干扰特征为在真实回波范围产生密集的距离假目标,达到欺骗性的压制干扰效果。
由图1、图3可知,移频调制类灵巧干扰的频谱宽度比不移频时略有减小,在时域上比真实目标要有所超前,这是由于进行了移频处理,使信号不再与滤波器匹配,从而使干信比降低,移频量过大对灵巧干扰效果不利。
3.2 二相编码信号噪声移频灵巧干扰仿真
下面对二相编码信号噪声移频灵巧干扰的时频域联合分布进行仿真验证,仿真信号参数设置为时宽T=169 μs,子脉冲宽度τ=1 μs,信号形式为13×13组合巴克码,载波中心频率f0=2 MHz,采样频率20 MHz,采用高斯白噪声移频调制,干扰增益10 dB,结果如图4所示。
由图4可见,噪声移频干扰使回波信号的旁瓣电平有所抬升,并且当移频量增大时主瓣也会恶化。所以,灵巧干扰对二相编码信号的干扰效果主要表现为使回波主瓣和旁瓣的结构发生变化,影响对目标的距离分辨能力。
由图2、图4可知噪声移频类灵巧干扰可使二相编码信号的回波周围出现大量杂乱分布的干扰点,并且由于二相编码信号的多普勒敏感性导致回波主瓣和旁瓣的结构也产生了严重的崎变。
4 结束语
灵巧干扰以其技术的先进性和干扰的灵活性必将在未来电子对抗中发挥出越来越重要的作用。本文采用时频分析的基本方法——短时傅里叶变换来提取出噪声移频类灵巧干扰的特征,仿真信号参数对干扰效果的影响,有利于解决新型电子对抗系统探索和设计中的相关问题,进一步推动灵巧干扰技术的发展,在军事领域具有十分广阔的应用前景。
[1] SCHLEHER D C.Electronic Warfare in The Information Age [M].Boston,American:Artech House,1998.
[2] BAUMELA L,MARAVALL D.Real-time target tracking[J].IEEE Transactions on AES,1995,10(7):947-955.
[3] GRIIFFTHS H D.New ideas in FM radar[J].IEE Electronics and Communication Engineering Jounnal,1990,2(5):185-194.
[4] 王雪松,肖顺平,冯德军,等.现代雷达电子战系统建模与仿真[M].北京:电子工业出版社,2010.
[5] 邱杰.灵巧噪声干扰本质含义探讨[J].海军航空工程学院学报,2011,26(5):481-484.
[6] 周政,唐宏,张永顺,王春阳.基于时域采样的灵巧噪声干扰研究[J],现代雷达,2010,32(5):53-55.
[7] 宁斐,唐斌.一种灵巧式欺骗干扰原理及实现[J].微计算机信息,2008,24(18):74-76.
[8] 董建华,顾汉明,张星.几种时频分析方法的比较及应用 [J].工程地球物理学报,2007,4(4):312-316.
FeatureExtractionofSmartNoiseFrequency-shiftJammingBasedonShort-timeFourierTransform
GONG Jian1,2,ZHANG Lei3,CHENG Chen4,XIONG Wu5
(1.Xidian University,Xi'an 710071,China;2.Air Force Engineering University,Xi'an 710051,China; 3.Unit 66133 of PLA,Beijing 100043,China;4.Unit 93792 of PLA,Langfang 065000,China; 5.Unit 94907 of PLA,Nanchang 330013,China)
The smart jamming has both characteristics of suppression jamming and deception jamming.The main technique indexes are about the characteristics of instantaneous change and random creation.As a conventional tool of signal processing,Fourier transform is only adapted to determined signal and smooth signal,and can not perform effective analysis to smart jamming.Aiming at the problem,this paper uses short time Fourier transform to extract the characteristics of smart noise frequency-shift jamming,simulates the influence of signal parameters on jamming effect,educes some conclusions that can help the research and countermeasure of new synthetical electronic jamming system.
smart jamming;time frequency analysis;noise frequency shift;short-time Fourier transform
2017-01-21
国家自然科学基金,项目编号:61601502;航空基金,项目编号:20150196007,20150196003,20160196003
TN972.2
:A
:CN32-1413(2017)03-0001-04
10.16426/j.cnki.jcdzdk.2017.03.001

