浅谈高中数学教学中如何培养数学建模能力

摘 要：数学建模是运用数学思想、方法和知识解决实际问题的过程，现已成为不同层次数学教育的重要和基本的内容，是数学学习的一种新的方式，为学生提供了自主学习的空间，有助于学生体验数学在解决实际问题中的价值和作用、体验数学与日常生活和其他学科的联系，增强应用意识。

关键词：数学建模能力；精致课堂

数学课程标准对数学建模教学提出以下的要求：在数学建模的教与学的过程中应充分发挥数学建模的教育功能，培养学生的数学观念、科学态度、合作精神；激发学生的学习兴趣，培养学生认真求实、崇尚真理、追求完美、讲究效率、联系实际的学习态度和学习习惯。很多选拔考试中也渗透了这方面的知识，因此，培养学生的数学建模能力是很重要的。本人通过对新教材的教学，结合新教材的特点和研究性学习的开展，对如何培养学生的数学建模能力和精致课堂理念进行探索，结合精致课堂要求的“三环五步”，现就如何提高数学建模能力谈下几点体会：

一、重视各章节前问题的教学，做好预习反馈，使学生明白数学建模的实际意义

教材的每章前都有实际问题的引入，上课时让学生明确学习本章后，能用相关数学模型去解决这些问题，让他们明白生活中或历史上存在的很多问题都与数学有关，培养他们的兴趣，也对数学建模知识有了渴求。如新教材必修四提出“物体做匀速圆周运动时位置变化的周期性，做简谐运动物体的位移变化的周期性；交变电流变化的周期性；四季的更替等。用数学知识如何刻画这种变化呢？”

通过学生的思考讨论，引出周期函数，然后讲解周期函数的概念，归纳其特点，展开新课程的教学，教导学生遇到周期性问题可以考虑用周期函数的相关知识去解决。

二、通过几何、三角形测量问题和列方程解应用题的教学，呈现目标，进行合作探究，渗透数学建模的思想与思维过程

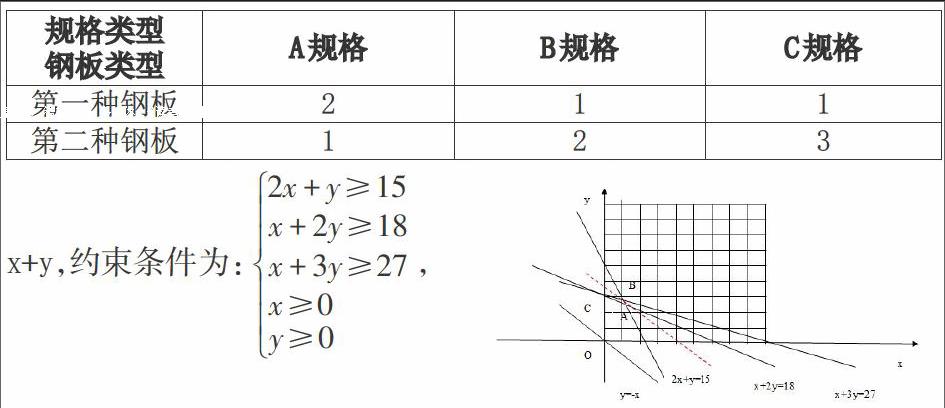
在教学中对学生展示建模的如下过程：现实原型问题→数学模型→演算推理→数学模型的解→现实原型问题的解→返回解释。数学建模过程的重点及难点就是据实际问题特点，通过观察、类比、归纳、分析、概括等基本思想，联想现成的数学模型或变换问题构造新的数学模型来解决问题。这时就要教会学生如何审题，找出关键点出来，再联系到所学过的知识来建立模型。例如，两种大小不同的钢板可按下表截成A，B，C三种规格成品：

某建筑工地需A，B，C三种规格的成品分别为15，18，27块，问怎样截这两种钢板，可得所需三种规格成品，且所用钢板张数最小。

分析：这是一道线性规划问题，关键在于求钢板张数就是求整数解，当所得最优解不是整数时，须在可行域内调整。

作出可行域如图所示：

令目标函数z=0，作出直线l：y=-x，平行移动直线l，发现在可行域内，经过直线x+3y=27和直线2x+y=15的交点A（18/5，39/5）可使z取得最小，由于18/5，39/5都不是整数，而最优解（x，y）中，x、y必须都是整数，因此可行域内点A不是最优解.通过在可行域内画网格线发现，经过可行域内的整点且与原点距离最近的直线是x+y=12，经过的整点是B（3，9）和C（4，8），它们都是最优解。

答：要截得所需三种规格的钢板，且使所截两种钢板的张数最少的方法有两种：第一种截法是截第一种钢板3张，第二种钢板9张，第二种截法是截第一种钢板4张，第二种钢板8张，两种方法都最少截两种钢板共12张。

这道题目再现了解建模题目的整个过程，其中在找最优解的B和C两点时，可以采用代入法验证，那样可以更快得出结果，比较适合基础较差的学生，不过过程就不够严密。

三、结合各章研究性课题的学习，探究提升，培养学生建立数学模型的能力，拓展数学建模形式的多样性与活泼性

数学的学习给人的感觉总是很枯燥乏味，因此学生的学习兴趣不是很浓，很多学生直接说：“如果不是为了高考，我才不学数学呢！”可见，“恨”和“怕”到了什么程度啊！当然数学由它本身的性质决定了有时学习起来确实很枯燥，何况那么长的实际应用问题，阅读都是困难的事情，还要理解并解答，确实是令人感到头痛！不过新课程标准下，教材有了很大变化，增设了很多实用性和趣味性的内容。如果老师能够结合到这些内容来进行展开，学生的兴趣很容易就激发出来，从而有了信心和动力，也培养了能力。

例如，讲完了必修1后有个实习作业“了解函数形成和发展的历史”。我布置了任务：每个小组完成一个选题，只要和函数有关的都可以。结果不少学生搜集了著名数学家们的故事，还写了感想。然后我就把他们搜来的资料分发给其他学生让他们感受数学家之所以成“大家”的过程，激发他们的兴趣。

四、培养学生的其他能力，及时总结，完善数学建模的思想和技巧

数学应用题的解决关键在于建立数学模型，数学建模能力不是一步到位的，需要其他知识方法和能力的累积。

首先，需要在平常的讲课中，为学生打下牢固的基礎，否则在审题酝酿的过程中就会一筹莫展，无法找到合适的模型。

其次，引导学生博览群书，多看各种各样的应用题。我们面对突发事件和状况往往会比较慌张，而熟悉的情况处理起来得心应手，解题也是一样，面对不熟悉的题目心里就会没底，解答起来也就没有那么顺手，但是如果面对熟悉的题目解答就很容易了。

再次，教导学生多留意身边的实际问题，养成善于观察，善于发现并提出问题的良好习惯，加强数学的应用意识。

然后，教导学生及时总结解题的方法技巧，积累相关的经验。

最后，健全临场发挥的心理品质。俗话说：“智者千虑，必有一失”。不管平常准备得如何充分，能力储存到什么程度，毕竟都是有限的，在考场上仍有可能受到挫折。这时就需要有充分的思想和心理准备，树立信心，实事求是，抱着一颗平常心去面对，就可以正常发挥甚至超常发挥自己的水平。

参考文献：

[1]兰永胜等.数学思想方法与建模技巧[M].青岛海洋大学出版社，2000.

[2]普通高中数学课程标准（实验）解读.江苏教育出版社，2004.

作者简介：

杨小玲（1980—），女，广东湛江人，领南师范学院数学与应用数学专业毕业，现任教于湛江二中港城中学.