建构主义环境下高中数学教学模式的应用
陈修宝
【摘 要】建构主义环境下,学为中心的意识得到充分认可。本文从|创设情境、协作对话、和进行意义建构等方面,阐述建构主义环境下高中数学教学模式的应用。
【关键词】建构主义;高中数学;教学模式
建构主义认为,学习环境是学习者可以在其中进行自由探索和自主学习的场所。与建构主义学习环境相适应的教学模式为:“以学生为中心,在整个教学过程中由教师起组织者、指导者、帮助者和促进者的作用,利用利用情境、协作、会话等学习环境要素充分发挥学生的主动性、积极性和首创精神,最终达到使学生有效地实现对当前所学知识意义建构的目的”。那么,这种教学模式如何具体地应用到高中数学教学中呢?笔者以“函数奇偶性”的为例加以论述。
一、创设真实情境,提供建构前提
建构主义提倡在教师指导下的以学生为中心的学习,追求教与学的合作化,并强调创设真实情境,把创设情境看作是“意义建构”的必要前提。因此,教师要考虑创设有利于学生建构情境的问题,从而使学生能利用自己原有认知结构中的有关知识与经验去同化当前学习到的新知识,赋予新知识以某种意义。如果原有知识与经验不能同化新知识,则要引起“顺应”过程,即对原有认知结构进行改造与重组。“数学情境”是从事数学活动的环境,是数学行为产生的条件,学生从中获得信息,通过联想、反思,发现数、形、结构及关系之间的联系,进而提出问题、研究问题、解决问题。
由于在学习函数奇偶性之前,已经学习了函数的概念和函数的图象,学生具备了利用函数解析式研究图形性质的知识基础,同时考虑到初中又学习了中心对称和轴对称图形,因此,可创设情境:
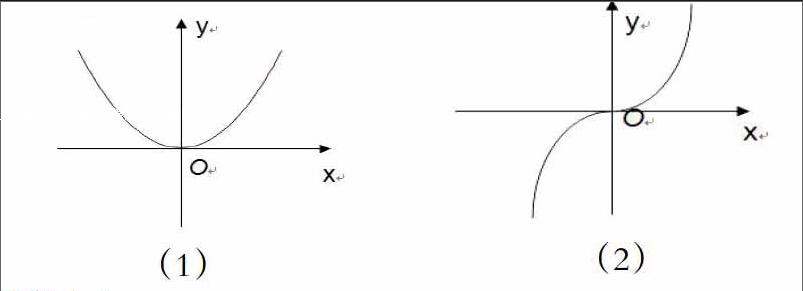
问题1:图(1)、(2)具有怎样的对称关系?
问题2:能否从函数表达式y=f(x),x∈D的角度对“关于y轴对称”和“关于原点对称”提出值得研究的问题?
(在这里调动学生已有的知识和经验,提供他们提出问题的基础,让学生自然提出问题。)
经过思考和考虑,可得出:
⑴y=f(x),x∈D满足什么条件时,其图象关于y轴对称?
⑵y=f(x),x∈D满足什么条件时,其图象关于原点中心对称?
至此,教师通过调动学生已有的认知结构,引导学生提出问题,展示知识发生过程,从而创设情境。
二、立足学为中心,坚持协作对话
建构主义认为,学习者与周围环境的交互作用对于学习内容的理解和知识的意义建构起着关键性的作用。对话和协商是意义生成和发展的途径,是个体所构建的知识获得“合法性”的方式。通过互动、协作、讨论等一系列活动,教师与学生、学生与学生的知识与思维得到了共享交流,从而学习者群体完成了对所学知识的意义建构。在数学教学中,“协作”、“对话”贯穿着始终。因此,教师应结合教学内容、根据学生的具体情况组织学习者对当前所学知识的概念、基本原理、基本方法和基本过程进行讨论与交流,并对协作学习过程进行引导,使之有利于学习者的主动探索和自主发现,更多更好地获取关于客观事物规律与内在联系的知识,向发展联想思维和建立新旧概念之间联系的意义建构的方向发展。教师要提出适当的问题以引起学习者的思考和讨论,在讨论中设法使之感到课堂教学轻松,从而使学生主动观察、主动思索、积极参与、发表意见、交流信息、相互启发、畅所欲言,在不断肯定、修正自己的思维过程中实现自我构建。
1.观察图(1)、(2),请根据已有的知识和方法设计出你对⑴、⑵的研究方案。
回到“情境”,再次调动学生已有的知识和经验,使学生很容易地从图像到具体的函数:y=x,y=x。
学生通过思考、讨论、交流与协作作出如下方案:
对于研究问题⑴
先考虑特殊情形。
举出图象关于y轴对称的函数,如:y=x,并与描点绘图过程相对应发现,图象关于y轴对称的根本原因是其上的点关于y轴对称的点仍然在图象上,即-x与x对应相同的函数值。
再抽象上升到一般情形。
函数y=f(x),x∈D的图象关于y轴对称
<=>图象上任意一点(x,f(x))关于y轴对称的点(-x,f(x))仍然在图象上。
<=>(-x,f(x))满足y=f(x),x∈D
<=>f(x)=f(-x)( x∈D)
于是,当且仅当f(x)=f(-x)( x∈D)时,函数y=f(x),x∈D的图象关于y轴对称。——(1)
再用类似方法研究问题⑵。学生得出结论:
当且仅当f(-x)=-f(x)( x∈D)时,函数y=f(x),x∈D的图象关于原点对称。——(2)
三、进行意义建构,增强自主意识
荷兰数学家Freudenthal提出,學习数学的唯一正确方法是实现“再创造”,也就是说由学生本人去发现或创造出要学的东西,教师的任务是引导和帮助学生去进行这种再创造的工作。数学的“再创造”过程不仅可以还原知识的产生过程,使学生真正理解,而且有利于发展学生自主学习的意识和独立思维的能力。
前面研究了简单情形——图象关于坐标轴和原点的对称性的情况,在此基础上应引导学生通过一般化进行拓宽与引申,提出更一般性的问题。
⑴y=f(x),x∈D满足什么条件时,其图象关于直线y=b对称?
⑵y=f(x),x∈D满足什么条件时,其图象关于直线x=a轴对称?
⑶y=f(x),x∈D满足什么条件时,其图象关于点(a,b)中心对称?
⑷y=f(x),x∈D满足什么条件时,其图象关于y=x对称?
⑸y=f(x),x∈D满足什么条件时,其图象关于直线y=kx+b对称?
以上问题可引起学生更深入的探讨,实现以再创造为目标的意义建构。
当然,建构主义学习环境下的数学教学模式具体应用的方式还有很多,如:强调利用各种信息资源来支持“学”(而非支持“教”);强调“过程教学”重于“结论教学”;强调“社会环境”;强调“同化学习”和“顺应学习”等等,并且,各种教学模式不是孤立的,而是有机联系的。总之,教师应根据教材的不同内容和学生的认知水平灵活加以运用,为促进学生建构活动的顺利进行创造良好的“环境”,应通过自己的工作向学生展现出“活生生”的数学思维活动过程,揭示出数学知识所蕴涵的数学思想方法来,从而帮助每个学生最终都能相对独立的完成数学建构活动,达到数学素质教育的目标。

