见微知著，优化教学

肖雄伟

[摘 要] 教学的过程是从未知向已知不斷生成的过程，生成不可一蹴而就，而应该关注于“微”处，通过细微处教学的精细化实现课堂教学的有效、高效.

[关键词] 高中数学；微；教学；目标；问题

教学的过程是动态生成的过程，早在1974年，美国的心理学家维特洛克发表了《作为生成过程的学习》一文，文章把“生成学习”作为一个观点做了明确表态，并且从心理学的角度论述了“生成”这一概念，随着当前新课程改革的深化，“生成性教学”被越来越多地提起，对于高中数学教学，如何借助于生成性教学模式促进教学效果的提升呢？笔者认为应该抓住一个“微”字，教学环节的“微化”、教学目标的“微化”、问题的“微化”、思路的“微变”等等，见微知著促进知识、方法、能力的生成.

[?] 微化环节，提高课堂效率

教学是复杂的过程，如何提升课堂效率呢？笔者认为需要我们教师在教学设计的过程中结合教材的特点和学生的具体学情进行精致化的处理，将一整节课进行“微化”和拆解，让我们每一个教学环节都能够贴合学生的具体学情，实现因材施教.

例如，“函数概念”这节课，笔者在教学环节的设计上进行了如下的“微化”.

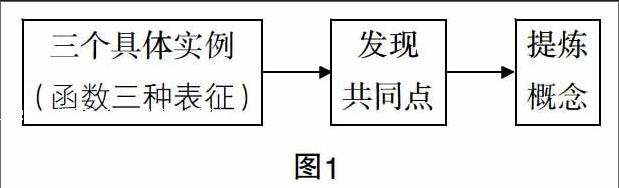
从教材设计来看，粗线条地分割课堂环节，可以将一整节课分层如下3个模块（如图1所示）.

这样的设计看上去毫无问题，但是实际教学中却不是很理想，为什么？仅仅给学生提供几个生活中的实例，学生很难发现其中存在的共同点，提炼和抽象出概念就更困难了. 为什么？因为教材的编排对学生而言存在着较大的知识与思维跨度，怎么办？必须合理地调整教材教学内容的顺序，同时将教学环节“微（观）化”，使其符合学生的学习心理特征，提高课堂教学的实效，笔者对于这节课的教学环节进行了如下的设计.

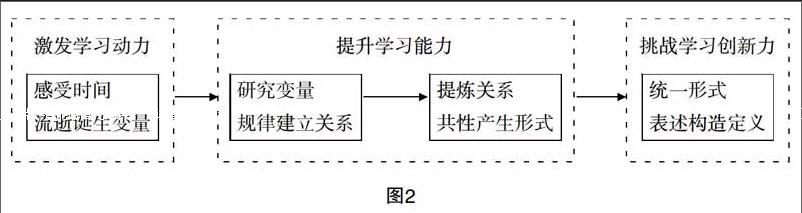
站在数学知识的系统性角度来看，联系函数三种表征的核心是“变量”，学生对变量是有认知基础的，但是认识存在片面性，我们在教学之初就应该让学生清楚地意识到其在函数中所扮演的角色，为此在教学环节的设计上选择了从“了解变量”入手，以此为基础将“函数”的三个表征进行有效的串接，最终统一表述概括为可以揭示函数本质的定义.

实践经验表明，我们要想提升课堂教学的效率，就必须结合学生的学龄特点将我们教学的每一个环节做到精细，确保学生每个环节的情感体验都是正向和积极的，都能将原有的认知经验和新问题的解决联系到一起.

[?] 微化目标，明确重、难点

“目标来源于并运行于活动之中……是活动中而非活动的转折点”这个观点得到了诸多教育学家的肯定. 新课程改革以来，我们大家对“教学目标”有了新的认识，教学目标不应该是单一性的，它是教师与学生在知识的平台上互动交流、切磋学习产生的一个丰满的体系，具有丰富的层面以及各个层面的不断扩展、延伸. 因此，在这样的理论引导下，初期教学的策划、目标的树立本身就应该设立为明确的“微化目标”，借助于对教学目标的微化，将真正的重、难点凸显出来，提高课堂教学和探究方向的明确性.

例如，关于“函数单调性”的教学，从教学重、难点上看，本节课主要目标是要引导学生发现如何运用多个维度的数学语言对“函数单调性的定义”进行有效的描述和表征，让学生充分体验对函数单调性的定义进行描述的过程. 既然确立了这样一个目标，那么我们在教学过程中就应该向着这个目标努力，课前我们应该有这样的思考：如果进一步微化重、难点，数学语言又可以从图形、文字、符号三个方面进行，难在哪里呢？图形、文字都不难，但是都仅仅是定性的描述，显然是不够准确的，因此通过目标的微化，本节课的教学目标就被锁定在了如何运用“符号语言”来定量地刻画函数单调性这个问题上.

[?] 微变问题，促进生成

数学知识和方法的生成是一个复杂而漫长的过程，如果我们不注重问题设计的精细化，难以给学生留下深刻的印象，问题微型化、微变化能够深刻刻画数学概念，提高学生对数学知识的理解程度.

仍然以“函数单调性”的教学为例，为了促进学生运用数学符号来表征和刻画数学概念，笔者在问题设计的细微处进行多次微变与追问.

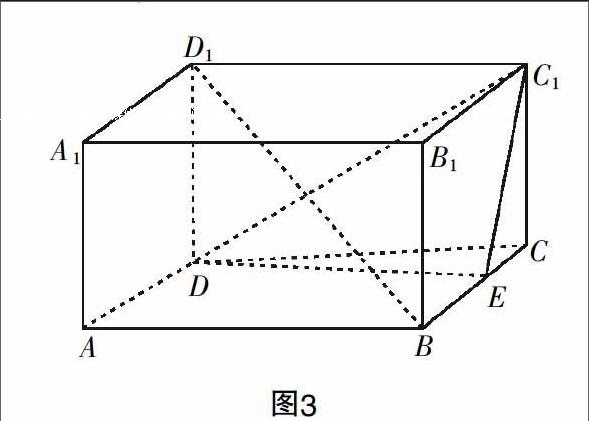
问题1：是否可以由1<2<3<…<99<100时f（1）

引导学生从作图的角度进行问题解决的推演，将符号语言与图像语言相结合，但是学生的认识往往还停留在定性的层面，如何促进认识的深入呢？可以将问题微变.

问题2：如果f（2）

问题2的设计是为了让学生接近准确的数学语言表述，但是不要急于给学生下定义，而是让学生充分地体验“任意”二字，在学生认识形成后，可以将认识与函数图像的几何意义相结合，结合几何意义（借助于图像在区间内任意两点连线斜率的正、负来分析），进行比较，当然对于初学者而言，要想很好地理解单调性还是有难度的，等学习了导数后就可以深入概念的数学本质.在得到定义后，还可以对定义进一步探究.

[?] 微变思路，发散思维

最终数学学习的效果是通过解决问题来反馈的，而很多学生反映课堂上能听懂，做题时总是思路理不顺，其根本原因在于学生的思维没有被有效打开，容易出现思维定式或“漏洞”. 为了促进学生思维发展，我们在教学过程中一定不能满足于问题的解决，还应该关注于解题思路的微变与拓展.

例1：如图3所示的长方体ABCD-A1B1C1D1中，E为BC的中点，求证：BD1∥平面DEC1.

思路1：从解题的思路上来看，很多教师和学生满足于“中心投影”法：BD1∥OE（O=DC1∩CD1，构建三角形中位线），如果我们教师在这个问题的解决中只满足于运用这个思路来完成例1的解答，那么不利于思维的发散，除了这个思路还有其他的思路么？给学生足够多的时间，学生就会将思维的方向进行拓展与延伸.

如何转化可以证明线面平行？稍加停顿，学生就很自然地联系到“线线平行”或“面面平行”，思路也就随之而来.

思路2（平行投影法）：具体的思维方向有2个：（1）BD1∥DG（G=B1B∩C1E）；（2）BD1∥C1H（H=AB∩DE）.

思路3（转换法）：设E1为B1C1的中点，从平面DEC1与平面BE1D1之间存在的位置关系入手，将线面平行问题转化为面面平行问题.

思路4（向量法）：（1）借助于“基底”进行推证；（2）借助于空间直角坐标进行算证.

当然，也并非所有的数学问题都能联系到多种解决问题的方法，但是这种有意识地拓宽解决问题思路的做法值得我们每一个数学老师在教学过程中进行尝试，因为我们教师有意识地拓展思路会对学生有潜移默化的影响，长期的浸润有助于学生科学素养和发散性思维的提升.

总之，我们教育的目的最终是发展学生的综合素养，对于高中数学而言要发展学生的理解力、创造力、情感、态度等等诸多方面，因此教学环节、问题和思路的引导不可过于粗犷，多从“微”处着手与展开，顺应素质教育的要求，长期下来，有助于提升学生思维的缜密性和创新性，甚至于有些是我们教师所没有想到的新的观点、新的认知，这些生成显然不是学生死记硬背的结果，而是“微”教学的成果. 我们把每个细微之处做实了，在借助于运用、拓展、串联等方式将学习的成果进行整合最终获得的将是更为稳固的知识与能力.