遵循规律，导之有方

王海华

摘 要：要掌握正确、清晰、完整的数学概念，既依赖于学生的数学认知状况，又依赖于教师的教学措施。笔者以“什么是周长”教学为例，尝试从教材、学生入手，根据学生的学习起点，关注“周长”概念的本质，探寻概念教学的有效方法。

关键词：周长；概念；本质；建构

数学概念是事物空间形式和数量关系的本质属性在人脑中的反映，是进行数学思维的基本要素。只有正确理解和掌握数学概念，才能有效进行判断、解释、推理、运算与解决问题，因此概念教学在数学教学中具有十分重要的地位。

回顾近年来数学概念教学的普遍情况，笔者发现有三点不足：首先，概念教学过于模式化——从举例、提出定义、复述、例题讲解到练习巩固，程式化明显，缺少对具体问题的具体设计；其次，课堂概念教学在目前的课堂上往往姗姗来迟——不少教师会在概念教学前边加一段故事情节，美其名曰是“情境创设”，却没曾想绕来绕去，冲淡了核心概念的探讨；当然，有些教师则认为概念教学是简单易懂的事，没必要讲，或者简单带过，等做作业时出了问题才幡然悔悟。

为了更有效地帮助学生深刻理解概念，让概念学习过程成为一个主动建构意义的过程，教师必须遵循教育心理学的基本理念，了解小学生的认知特点，结合学生的学习基础，从多方面入手进行概念教学。下边以“什么是周长”为例进行分析，以求教于同行。

一、直观情境引路，建立表象

表象是事物不在眼前时，人在头脑中出现的关于事物的形象。在数学概念中要十分重视表象这座桥梁的运用，让学生在积累了丰富感性认识的基础上，通过表象过渡进行科学的抽象，并上升为理性认识。

【案例呈现】

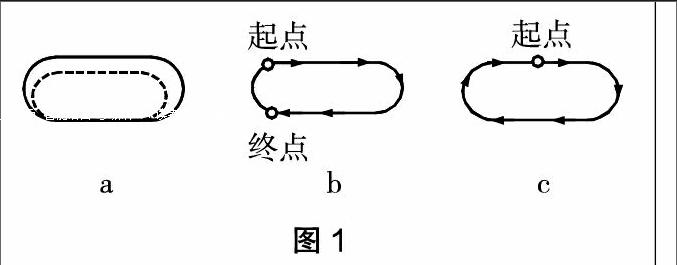
师：爸爸给小明制定了一个锻炼计划，让他每天围着操场跑一圈。我们看看小明是怎么跑的？（指图1a，实线是操场的一圈，虚线是小明跑的路线）

师：他跑的跟你想的一样吗？应沿着操场的哪儿去跑？请指出来。

生（指图）：沿着实线跑。

师：这条实线是操场的边线，那么第二天小明又跑了（图1b），请问第二天是否符合要求？

生：小明没跑完。

师：你觉得他应跑到哪儿？请上来指一指。

师：虽然他沿着边线跑，但要从起点跑到哪里？

生：起点。

师：沿着边线跑，从起点跑回到起点，这样才叫跑一圈。

师：接下来第三天，小明跑得对吗？（图1c）

生：对。

师：谁来说说，小明是怎么跑的……

师：一圈就是一周，今天我们就来学习周长。（板书：周长）

这里笔者首先给学生们呈现了小明跑的一周，但没有沿着操场的边线跑，紧接着沿着边线，但没有跑完，最后呈现怎样跑才是操场的一周。通过三天不同的跑步方式，层层递进，将周长的三个要素（沿边、总长、封闭）孕育其中，很好诠释了周长的概念。由此可见，周长的表象建立必须通过对直观形象的直接操作才能获得，这符合小学生以形象思维为主的特点，有助于抽象概念的建立。

二、多种感官参与，触摸属性

著名的心理学家皮亚杰说：“知识来源于动作。”在以活动操作为切入点的几何概念引入过程中，教师应指导学生做到眼、耳、手、口、脑并用，让学生主动地探索新知，发展思维，从而抽象出几何概念的表象。例如在引出周长的概念后，笔者设计了下面这张“活动与作业”并用的作业纸（如图2）。

【行为分析】笔者在学生初步感知“什么是周长”后，从学生身边熟悉的事物——树叶引入。在描的过程中对树叶的周长有了初步的感知。随后再给学生提供多种图形，描一描，建立对周长的丰富感性认识，特别是五角星图和篮球场图，学生容易产生误解。通过对比、观察，学生深刻地掌握了周长的内涵。在学生认识了平面图形的周长之后，再引导他们从生活中找一找物体的周长，并且摸一摸。这样做，一方面丰富了学生的感性体验，将他们对周长的认识加以拓展；另一方面，将数学知识与生活实际紧密联系起来，使学生感到数学无处不在，增强学好数学的信心。设计量一量这个環节的目的是想让学生感受到周长在实际生活中的应用，并且通过测量来加深学生对周长的认识。

三、学习问题解决，深化内涵

完整的学习过程是发现问题、提出问题、解决问题的过程，教师始终要善于抓住身边的素材，注意让学生经历知识的发生发展过程，感悟知识的本来面目，加深对数学概念的深入理解，让学生在“再创造”中得到知识、情感、态度和价值观的充分发展。如图2中“我来量一量 算一算周长”这个环节的教学：

师：选择你最喜欢的一个图形，量一量它的周长，并把测量结果记在表格里。你在量的时候碰到什么困难？

生：有，树叶？

师：怎么量？

生：用软尺或绳子。

师（演示）：先把绳子绕着树叶一周，再在绳子上做好记号，拉直后用尺子量出绳子的长度。

（同桌合作完成）

师：量一量其他图形，要求：同桌可以合作，自己选择材料。

反馈：你们量出了什么的周长？谁能再说说什么是周长……

小学生喜欢动手操作，这为测量周长的活动提供了一个很好的发展空间。笔者让学生运用准备的学具——软尺、线、软铁丝、直尺量算出身边图形的周长，然后小组交流方法，最后汇报。课堂上出现了两种情况：一是图形的边是直线时可以用量、算的方法求出它的周长；二是图形的边是曲线时可以用绕、量的方法求出它的周长。学生从中深刻体验到解决问题策略的多样化。在优化测量方法以后，学生的思维更加敏捷，知道要从不同角度去探索解决问题的多种方法和技巧，充分体验了自主解决问题的快乐，享受到成功的喜悦，有利于形成良好的数学认知结构。同时，通过测量与计算一些物体的周长，学生的思维得到了拓展，清晰而又牢固地再现了周长同边线之间的关系，加深了对“周长”概念的理解。

四、追寻不变之变，升华本质

对于概念的练习需要有变化，变化的往往是具体场景，不变的则是概念本身，用不变去“度量”变化，就能在变化中找到不变的本质。概念的正例反映了最有利于概括的关键信息，反证则反映了最有利于学生通过辨别突出概念的本质属性，如对于“在墙角设置三道篱笆围出一块菜地”这样的练习，其实就是出示了一个跟周长有关而又不是周长的练习。还有一种变化就是习题的变式，通过变化题目条件得出有可能变化的结论。

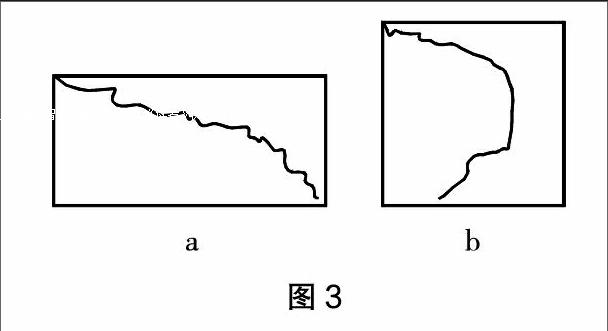
经过前几步的学习，学生对于周长有了一定的认识，但仍有很多认识模糊的地方，如认为面大周长就大，面小周长就小。笔者设计了一个练习：一个长方形（图3a）沿对角线撕开，分成的两半的周长哪个更长？如果一个正方形（图3b）沿画线撕成两部分，哪部分图形的周长更长？学生容易产生思维定式，这时教师不急于评论，让学生自己发现正方形和长方形撕纸方式的不同，这样学生的思维便可得到升华。

彭晓玫说过：“小学生学习数学的开始，就在于概念的学习的开始。”在建构概念的过程中切不能让学生生吞活剥，只有遵循从直观到抽象的思维发展规律，沿着“直观—表象—属性-内涵-本质”的路线进行探究，让学生多种感官参与进来，才能将概念从内涵到外延“连根拔起”，让学生在心领神会的同时获得心畅手快的成就感。