从“算法”走向“意义”

王婵丹

摘 要：平均数是小学数学统计与概率版块的一个基本概念。学生能比较容易地掌握平均数的计算方法，却常忽略平均数的特征及其意义。因此，教学“平均数”一课就需立足于学情调查分析，汲取教材给予我们的启示，从“情境创设追求真实性与可靠性”“不同维度切入达成意义建构”“习题多层开发体现统计价值”三方面，帮助学生更好地理解平均数的统计意义，从而形成数据分析观念，感悟其统计价值。

关键词：平均数；数据分析观念；统计意义

平均数作为一个常用的统计量，是小学数学统计与概率版块的一个基本概念，历来是课堂研究的重要内容。为了解学生在学习本课之前有哪些知识储备，认知和学习能力达到哪种水平，笔者对城乡三、四年级近200名学生进行了问卷调查，发现主要存在以下两个问题。

[调查问题1]

你听说过平均数吗？请用自己的语言说说什么是平均数？

[水平分级]

如表1，根据学生回答确定其对于“平均数”概念认知能力的水平级别。

[数据呈现]

三、四年级分别发放84份、134份问卷，收回有效卷84份、134份，统计情况如图1。

归因分析：知识负迁移，导致“平均分”与“平均数”混淆。

对于平均数意义的理解，三、四年级学生大多处于0～1级水平。虽然四年级学生总体认知水平好于三年级，但大多是基于“均分”的认识上。可想而知，学习过程中出现“平均数”与“平均分”概念混淆实属难免，关键在于课堂中如何帮助学生理解“每份”能代表一组数据的集中趋势，实现从“平均分”上升到对“平均数”意义的理解上。

[调查问题2]

比一比：男生与女生哪队踢毽子水平更高？

（1）要比哪队踢毽子水平更高，当人数不同时，你打算比什么？怎样比？

（2）你可以通过算一算或画一画等各种方式，说明这一队成绩好的理由。

[水平分级]

如表2，根据学生回答确定其对于“人数不同的两队如何比较踢毽水平”的能力水平级别。

[数据呈现]

三、四年级分别发放84份、134份问卷，收回有效卷84份、134份，统计情况如图2。

归因分析：经验缺乏，从“用总数”到“用平均数”出现思维断层。

从统计数据显示，处在1级水平即用“总踢毽个数”去比较两组水平的人占了多数。访谈处在1级水平的学生：“说说你为什么要比总数？”大多学生认为，把每个人的踢毽个数加起来就能代表整个队的踢毽水平。访谈处在0级水平的学生，发现有一部分真不知道该怎么比，还有一小部分学生认为，人数不同，比总数不公平，但想不到该用什么数来代表每个队的踢毽水平。由此可见，绝大部分学生对于平均数的意义及其统计价值是陌生的。

那么，教材能给予我们哪些启示呢？通过教材之间的横向与纵向对比，寻找在编排上的共性与区别，以求了解编排中的变化，寻求到问题解决的方法。

对比1：选取人教版例1（图3）与北师大版（图4）在统计素材上进行横向比较。

启发：基于合适情境的创设，把握“教”的方向。

从统计过程看，北师大版较完整地呈现了数据产生的背景，而人教版仅用图表呈现了数据整理后的结果。可见，有些内容不适合在课堂中经历统计过程，又缺失统计研究的价值。所以，统计素材的选择至关重要。

对比2：选取人教版2002年与2016年的教材，对同类素材不同编排上进行对比（图5）。选取人教版例2与北师大版，对意义建构不同路径上进行对比（图6）。

启发：基于有效路径的选择，明确“教”的方法。

纵向看，从“相同人数比较→不同人数比较”调整，教材更想凸显“用平均数去代表两组数据的总体水平，体现平均数的统计作用与价值”的意图。横向看，北师大版呈现同一个人连续数据的一般水平，人教版呈现一个小组分散数据的整体水平。这些调整变化以及编排上的不同，都给课堂建构“平均数”意义指明了路径与方向。

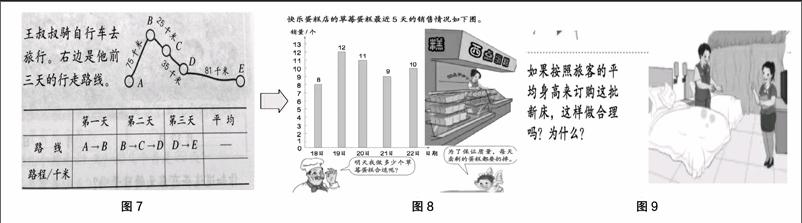
对比3：选取人教2002年出版的“平均数”练习课的最后一题（图7）与人教2016年出版的“平均数”练习课的最后两题（图8和图9），在习题演变上进行对比。

启发：基于习题演变的分析，核实“教”的目标。

过去的习题更侧重于“算法”的巩固，虽然在形式上出现图文结合，有时会涉及加权平均数的深化，但落脚点还是在于“算法”的理解。现在习题的考查点发生了本质变化，更关注学生对“平均数”意义的理解，更关注数据分析观念的建立，更关注对用统计结果做出合理推断与预测的能力的考查。因此，习题的改编与设计应倾向于这方面思考。

综上所述，无论是纵向的教材调整，还是横向的版本对比，都能发现教材对“平均数”这个统计量在素材的选择、算法的探究、意义的理解、习题的设计等方面做出了调整。其目的是想实现从“算法意义上的平均数”走向“统计意义上的平均数”。

那么，在教学“平均数”时，就必须顺应教材带给我们的调整与变化的启示，必须遵循学生的认知和能力水平，让学生真正融入统计领域，让数学课堂真正富有统计味道。

一、真实情境创设，体现统计价值

增强数据统计的真实性和可靠性，就必须坚持实事求是的原则，因为真实性是可靠性的基础，可靠性是真实性的外在表现，两者和谐统一，这也是教学“统计与概率”领域内容时必须遵循的原则。那么如何解决时间上的矛盾呢？

1. “延伸”课堂，克服時间不足的矛盾

实现与其他课程整合是延伸课堂时间、拓宽课堂空间的比较有效的途径。如：套圈个数的数据收集可以通过与活动课相结合；记数字情况统计可以创设一个课前的游戏环节；生日月份的统计可以与综合实践课相结合等。

[片段描述]

（1）课前五分钟：如图10，这是一个记数字游戏，考验同学们的记忆力，请大家把你看到的数字按顺序记在纸上，看看在3秒时间内你能记住几个？

（2）在这一轮游戏中，我们班最多记住了（ ）个，这是我们班的最高水平。还想再玩吗？

这一环节的设置，不仅创设了和谐轻松的学习氛围，而且还能让学生比较科学与真实地了解自己和同伴三秒钟记数字的水平，让统计的数据具有真实可靠性。更重要的是向学生传递了统计所做的研究是有现实背景和意义的，那么我们基于数据分析所做的推断是合理有价值的。只有这样，才能帮助学生建立科学的研究观，才能发展学生数据分析观念，感悟統计的价值。

2. 重置问题，数据呈现更趋合理化

教学平均数时往往会创设“再增加一个数据，看看平均数会发生怎样的变化”这一问题情境。但往往后续增加的这个数据，执教者可能因为要达成某个教学目标，会虚拟这个数据。

[片段描述1]感受极端数据

师：同学们，乙队的整体水平低了些，她们想再增加一名队员，你们觉得他们队有没有反败为胜的可能？（ppt展示如图11，感悟平均数被大大拉高的现象）

一生在座位上窃窃私语：王强能套这么多吗？

当提供一个极大数据时，学生对于“平均数易受极端数据的影响”感受比较深刻。但这个违背事实依据的数据，个别学生就质疑“这位高手怎么比另外三个人的总和还要多呢”。显而易见，这样的情景创设违背了科学性，统计结果就失去了其价值。现调整如下：

[片段描述2]

师：老师也加入了这场套圈比赛，你们觉得平均水平会有怎样的变化？

生1：我认为平均水平会高一些，因为老师的水平会比我们好一点，如果您套了15个，乙队的水平就能提高。

生2：可能还是7个，如果老师套了7个，那么平均数就不会发生变化。

生3：那也有可能会比原来的平均数要低，万一老师不擅长套圈呢。

可见，问题情境的调整不仅开放了学生的思维，更重要的是能引导学生根据现有的数据做出一个合理的分析，这样更有利于数据分析观念的培养。

二、不同维度切入，达成意义建构

基于学情调查与教材分析，一般会采取以下素材和路径来推进“平均数”意义的建构。

1. 立足“均分”经验，实现意义架构

基于学生有“均分”的经验，教师从“平均每份是多少”切入意义教学是比较顺畅的。但这层认知仅停留在把一个数均分后的结果上，学生很难把这些离散的点，当作一个整体看待。那么怎样实现“这一份的数字能代表这组数据的集中趋势或整体水平”呢，笔者认为可以增加“对比思辨”的环节，实现“统计意义”上的建构。

[片段描述]

想一想，我能说理。

师：通过刚才的研究，我们知道了平均数能代表一组数据的平均水平。现在请同学们想想图12中哪个问题能用“平均数”去解释？为什么？

生1：我认为第二个问题能用平均数解释。因为只要第三个花瓶给第二个花瓶一朵花，就能让三个花瓶的花同样多。

生2：我也认为第二个问题可以用平均数解释。因为通过“18÷3=6”就能求出每个花瓶可以插6朵花，这个6就是“6、5、7”这三个数的平均数。

老师见同学们认知基本达成一致，追问：那第一个问题呢？

生3：我觉得第一个问题虽然也是通过“18÷3=6”来计算的，但其实这道题是把18花朵平均分成三份，求每份是多少？

生4：我和生3的想法相同，这是二年级学过的平均分。

师归纳：同学们说得很有道理。其实“平均分”和“平均数”都可以通过“总数÷份数=每份的数”得到。但平均数的特点就是还能用这个每份相同的数，去描述一组数据的平均水平，就像生2说的那样，6是“6、5、7”这组数据的平均数。

此题是人教版例2中的做一做，当认识完“平均数”意义后，会有一部分学生仍存在混淆。此时，教师要直视这一现象，通过“题组式”对比，让学生用“平均数”的知识解释问题，再经历对比、讨论、思辨，渐渐明晰“平均数”的意义。

2. 站在“统计”高度，实现意义架构

如果课堂一开始就定位在“统计”高度上，即在学生思维的困惑处展开研究，学生就会跳出“平均分”的干扰，从统计学的角度认识、理解、感悟“平均数”的意义。但同时，我们也能预设到学生对“集中趋势”的理解是非常困难的。因此，在仔细研读了教材后，教学时就可以从“连续数据的一般水平”与“分散数据的整体水平”中展开意义探究。

如：北师大版教材采用的素材就是“淘淘一人五次记数字”的情境，对于这五个连续数据的平均水平的描述，教学中可以舍弃“集中趋势”，而采用“一般水平”的描述。

[片段描述]关注“连续数据的一般水平”

对比不同水平感悟，平均数代表一组数据的一般水平。

师：9可以说是淘淘5次记数字的最高水平，那4个呢（生说：最低水平）。那能用哪个数字来代表淘淘5次记数字的一般水平呢？

生1：我觉得是5，因为5不会太多也不会太少，在中间。

生2：我认为是6，因为刚才我们用移多补少法，得到了淘淘每次都能记6个（图14）。

生1：但6这个数字，一次也没有出现呀。（顿时教室里没有声音）

生3：如果每次都记5个的话，还可以让每一次再分1个（图15）。

老师引导学生感悟实际数据与平均数据的区别。

师：现在同学们想不明白的地方在于选5，还可以再分，选6，没有被套出来。

看样子，同学们已经关注到“平均数”最核心的部分了。其实，能代表一组数据平均水平的数，它不一定要真实存在，不一定真要有一次记住6个数字。它可以通过算与移的方法，让它们变得同样多。现在你们说说：可以用哪个数字代表淘淘记数字的一般水平？

生1：我认为是6，因为选6的时候淘淘这五次就同样多了。