改进的DFT插值频率估计算法及其DSP实现

郑 威 陈德昶 刘红星

(1.江苏科技大学电子信息学院 ,镇江,212003; 2.南京大学电子科学与工程学院,南京,210093)

改进的DFT插值频率估计算法及其DSP实现

郑 威1陈德昶1刘红星2

(1.江苏科技大学电子信息学院 ,镇江,212003; 2.南京大学电子科学与工程学院,南京,210093)

在Quinn算法和插值迭代算法(A&M算法)的基础上,提出了一种改进的离散傅里叶变换(Discrete Fourier transform, DFT)插值频率估计算法。该算法首先通过Quinn算法估计出1个频率误差作为迭代估计算法的误差初值,然后用迭代算法精确估计频率误差。改进后的算法可以有效减少迭代次数,因此同时具有Quinn算法的高效率和A&M插值迭代算法的高精度。为了提高算法在DSP处理器上的运行效率,本文还对算法在DSP上的实现提出了一种优化方法，有利于该算法的实时性应用。仿真结果表明该算法在频率估计精度、实时运算效率以及对噪声的抗干扰性能上均获得了提升。

频率估计；离散傅里叶变换插值；估计精度

引 言

信号频率估计是信号处理领域的一个重要问题，在很多工程问题上都有广泛应用，如语音信号处理中的基音周期估计、电网质量分析中的谐波及间谐波检测和生物医学信号处理中的心率估计等。在以上诸多应用中，如何得到观测信号频率参数的精确估计一直是研究的热点问题。正弦信号频率参数的极大似然估计可以通过被测信号的周期图最大极值获得[1-2]，但该方法计算比较耗时，且存在收敛性的问题。自回归模型(Autoregressive, AR)、Prony以及多重信号分类算法(Multiple signal classification, MUSIC)等现代谱估计方法涉及到相关和矩阵分解运算，不易硬件实现[3]。由于离散傅里叶变换(Discrete Fourier transform, DFT)可通过快速傅里叶算法(Fast Fourier transformation, FFT)迅速得到结果，便于实时处理[4]。通过搜索DFT离散谱线的最大幅值，其对应的谱线频率可作为真实频率的估计。但这是一个粗略估计，由于DFT变换的频率分辨率受数据长度的影响，并且存在栅栏效应，严重影响了频率估计的精度，其误差范围为±Δf/2,Δf为DFT谱线之间的最小间隔，即频率分辨率。当信号真实频率不是Δf的整数倍，采用矩形窗时，其位于主瓣内最大幅值谱线与其相邻谱线之间，而估计误差与这两条谱线的幅值之比有关。根据这一性质，采用DFT幅度比值进行插值成为一种精确估计频率的方法[5-15]。

在文献[7]中，Quinn利用最大谱线与其左右两条相邻谱线的DFT系数之比的实部来估计频率误差，从而得到真实频率的估计。该方法的优点是计算简单、效率高，但只能进行一次运算，估计精度受限。文献[8]中提出了一种基于DFT插值的迭代算法(A&M算法)，将频率误差进行迭代计算，不断逼近真实频率，提高了估计精度；但是由于每次迭代都需要进行乘累加运算，所以运算量比较大，导致算法的效率较低。由于迭代算法和Quinn算法的优缺点刚好可以互补，所以两种算法的结合可以保证在一定的估计精度下提高算法估计效率。本文利用Quinn算法估计的误差结果作为迭代算法的误差初值，提出了一种改进的DFT插值频率估计算法，并且对该算法在DSP处理器上的实现进行了优化，以提高算法在处理器中的运行效率。

1 DFT插值算法原理

1.1 Quinn算法

设待测的离散单频复信号为

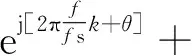
(1)

式中：A，f，θ分别为信号的幅度、频率和初始相位；w(k)为高斯白噪声。对信号的傅里叶变换结果为

(2)

假设mN为DFT变换最大谱线处的索引，则信号的真实频率为

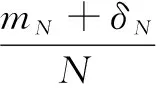
(3)

式中：δN为频率误差。只要计算出误差值就可以获取信号的真实频率f。文献[7]通过式(2)最终推出在忽略噪声情况下最大频谱与左右相邻频谱之间的比值关系为

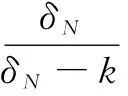
(4)

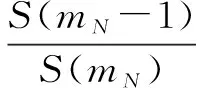
1.2 迭代插值算法原理

A&M算法通过搜索DFT变换结果获取最大谱线处的索引mN，然后计算出其左右一半频谱间隔处的DFT系数，通过频域插值算法计算信号的真实频率。由于mN应该最接近真实频率，所以认为δN在[-0.5, 0.5]之间。已知DFT系数计算公式为

(5)

文献[7]根据式(5)推导出

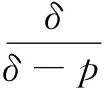
(6)

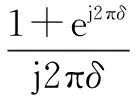
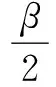
(7)

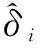
2 改进算法的原理与实现

2.1 改进算法

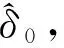
步骤1 对信号进行FFT变换，记下变换结果，并且对结果进行搜索找出最大谱线处的索引mN。

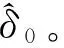
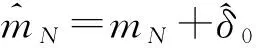
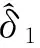
2.2 改进算法的DSP实现

根据算法的原理，整个算法可以分为3个部分。首先对信号进行FFT变换并搜索最大谱线的位置，然后通过Quinn算法计算出误差初值，最后把误差初值代入迭代算法计算出迭代1次后的误差值。由于TI官方提供的数字信号处理浮点库中的复数快速傅里叶变换(Complex fast Fourier transform, CFFT)不仅具有很高的精度，而且由于TI官方对库函数的实现进行了很好的优化，使其都具有很高的运行效率，所以这里的FFT变换直接调用官方的CFFT。对于Quinn算法，由于它的过程非常简单,所以对它的实现在这里不特别叙述。本文主要对迭代算法的实现进行分析，并提出了优化方法。由于在处理器上不能直接进行复数运算，所以必须对迭代算法的式(5)进行分解，考虑到式(5)变换结果的实部和虚部分别对应余弦和正弦变换的结果,所以令

(8)

则有

Sp=Spcos-jSpsin

(9)

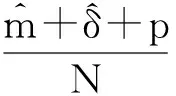
3 仿真分析

仿真分析在Matlab仿真环境和TI的TMS320F-28335处理器上进行，从算法收敛性、噪声对估计精度的影响以及算法的效率几个方面分别对Quinn算法、迭代算法和改进算法进行了仿真分析。在MATLAB仿真环境中对算法收敛性、噪声对估计精度的影响以及算法的效率进行分析比较。在TMS320F28335处理器上对优化效果进行仿真测试。

3.1 算法的收敛性分析

在进行收敛性分析时，对Quinn算法、迭代算法和改进算法在相同的条件下进行仿真实验比较3种算法的收敛性。仿真实验采用频率f在24.5～25.5 Hz之间，增量为0.1 Hz,相位θ为0的离散正弦信号，添加信噪比SNR为0 dB的高斯白噪声。采样频率f设为1 024 Hz，信号的长度N取1 024，作1 024点FFT变换。仿真中，对每个实验信号进行1 000次频率估计，统计每个实验信号估计结果的均方误差。迭代算法、改进算法以及Quinn算法随频率变换的收敛曲线如图1，2所示，其中比率R定义为R=频率估计均方误差(MSE)/CRB，R的计算公式在文献[7]中给出。

从图1可以看出迭代算法迭代1次、两次以及改进算法的收敛性都非常接近CRB，而且改进算法和两次迭代后的收敛性明显比只进行1次迭代要好。从图1，2可以看出，相对于迭代算法和改进算法,Quinn算法的估计精度相差太远。所以改进算法相对于迭代算法在减少迭代次数的同时能够有效地保证算法的估计精度，相对于Quinn算法的估计精度更有明显的提高。

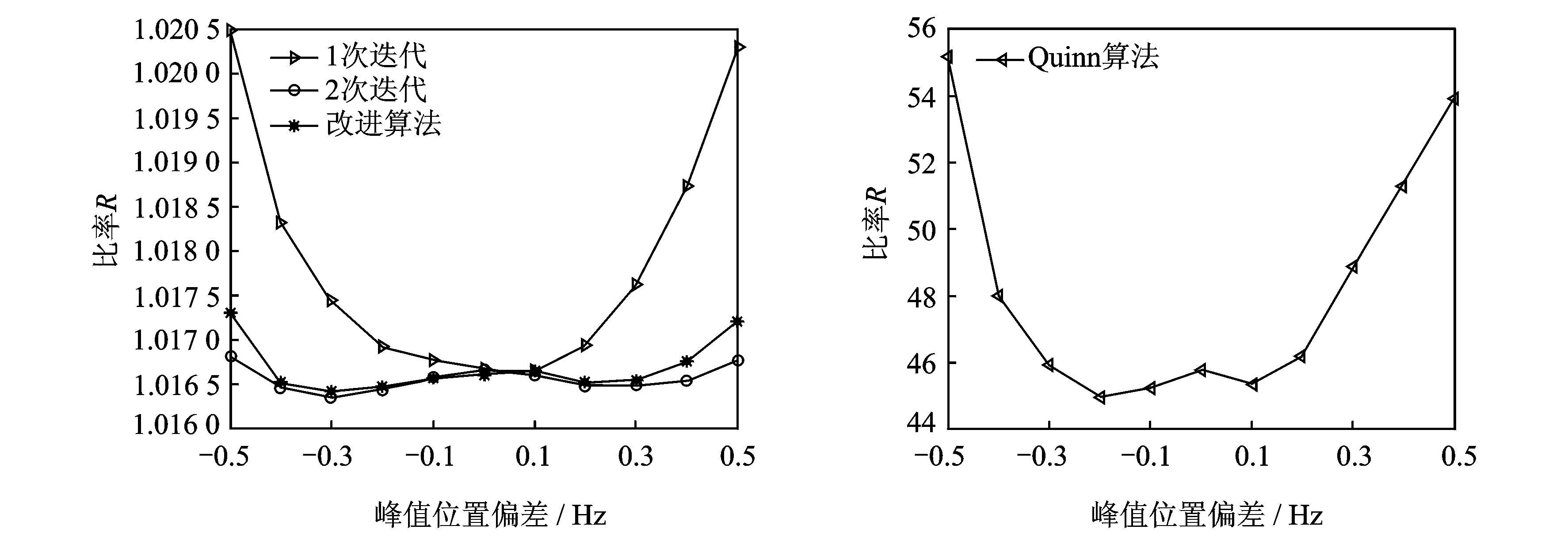
图1 迭代算法和改进算法的收敛性 图2 Quinn算法的收敛性Fig.1 Convergence of iterative algorithm and improved algorithm Fig.2 Convergence of Quinn algorithm

3.2 噪声影响分析

从收敛性分析结果得知Quinn算法与迭代算法及改进算法估计精度相差太大，所以这里主要分析改进算法和迭代算法的抗干扰性能。为了充分比较改进算法与迭代算法的抗干扰性能，分别对正对谱线处、偏离1/4频谱间隔处和偏离1/2频谱间隔处的几个频率进行分析。根据上述要求采用3个频率f分别为120，120.25，120.5 Hz的离散信号，信号的其他参数都与进行收敛性分析时相同，噪声为高斯白噪声，信噪比SNR取-5～5 dB，步长为1 dB。仿真中，分别在上述信噪比下对3个实验信号进行1 000次频率估计实验,统计不同信噪比下频率估计的均方误差。3个实验信号的频率估计均方误差MSE随信噪比SNR的变化曲线如图3～5所示。从图3～5可以看出，随着信噪比的提高均方误差变小，估计精度提高，并且均方差始终保持在千分之一数量级，而且实验信号频率越接近频谱，改进算法的噪声特性越接近于迭代算法。在信噪比大于0 dB时改进算法基本都可以保持和二次迭代相同的噪声特性。

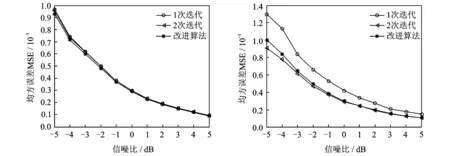
图3 正对谱线处 图4 偏离1/4频谱间隔处 Fig.3 Aligning at spectral line Fig.4 Deviation from 1/4 spectral line

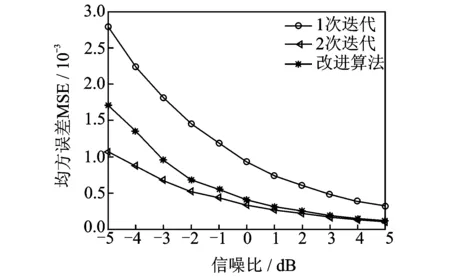
图5 偏离1/2频谱间隔处Fig.5 Deviation from 1/2 spectral line

Tab.1 Computing time of iterative algorithm and improved algorithm

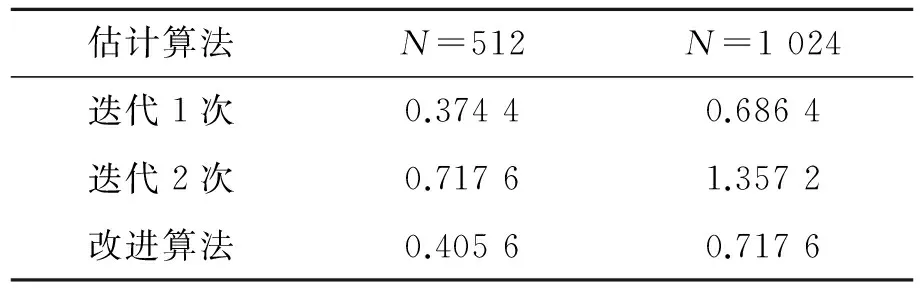
估计算法N=512N=1024迭代1次0.37440.6864迭代2次0.71761.3572改进算法0.40560.7176

所以改进算法和迭代算法一样都具有很好的抗干扰性能。

3.3 算法效率分析

在分析效率时,首先在Matlab中对改进算法和迭代算法的效率进行分析比较,分别对信号长度N为512和1 024时两种算法的效率进行统计,记录进行1 000次估计所需的时间，仿真结果在表1中。观察表1中的数据可以发现，改进算法的运算时间和1次迭代所需的时间非常接近，几乎接近于2次迭代所需时间的一半，所以改进算法在保持几乎相同的估计精度下，相对于原迭代算法的效率提高了近1倍。在TMS320F28335处理器和CCS软件上对迭代算法的优化效果进行分析，在FFT变换长度N分别为32，128，512和1 024时记录直接调用三角函数的周期数与进行优化之后算法程序运行的周期数，周期数=运行时间×处理器工作频率,结果如表2所示。对表2中的数据进行分析可以发现，把三角函数的计算优化为加减乘除运算后算法的效率提高了5～6倍，并且FFT变换长度N越大,效率增加的倍数越大，即优化之后算法的效率至少提高了5倍。

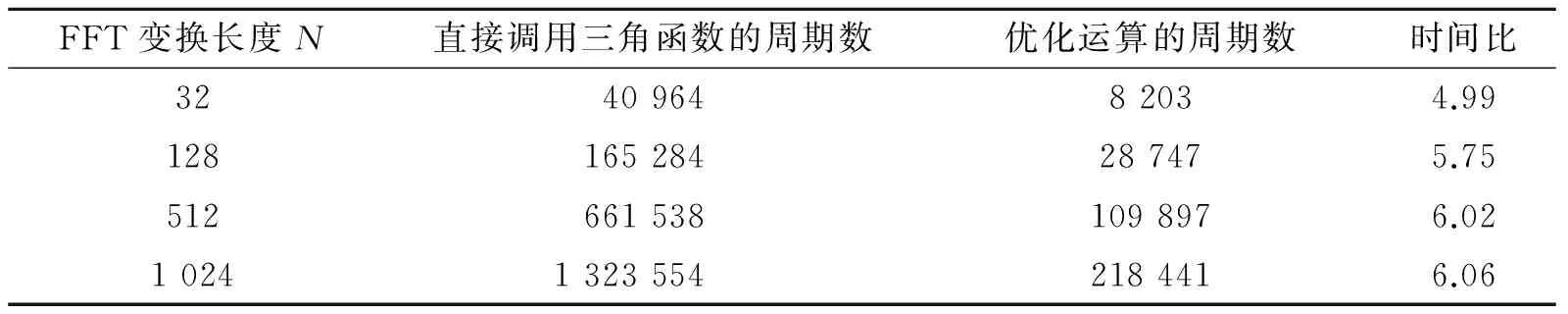
表2 直接调用三角函数与优化后运行效率对比

4 结束语

DFT插值频率估计算法兼顾了估计性能和运行效率，一直是频率估计研究和应用领域的热点，但如何将现有的算法进行融合，吸收各自方法的优势而获得既准又快的效果仍然是值得研究的问题。本文分析了Quinn算法和A&M迭代算法的原理及两者的优缺点，在此基础上提出了改进的DFT插值频率估计方法。并且对迭代算法在处理器上的实现进行了优化，提高了算法程序在处理器上的运行效率。在算法的收敛性、抗噪声性能以及效率等方面对算法进行了仿真分析和对比，验证了改进算法高精度和高效率的特性。本文所得结论可为DFT插值频率估计算法在各类实际应用场合下获得更好的估计精度以及实时性提供一些有益的参考。

[1] Abatzoglou T J．A fast maximum likelihood algorithm for the frequency estimation of a sinusoid based on Newton methods[J]. IEEE Trans ASSP, 1985,33(1):77-89．

[2] Rife D C, Boorstyn R R. Single-tone parameter estimation from discrete-time observations[J]. IEEE Trans Inform Theory, 1974,20(5):591-598.

[3] Tsui J. Digital techniques for wideband receivers[M]. USA: Artecth House, 2002:1-6.

[4] 齐国清，贾欣乐.插值FFT估计正弦信号频率的精度分析[J].电子学报，2004,32(4):625-629.

Qi Guoqing, Jia Xinle, Accuracy analysis frequency estimation of sinusoid based on interpolated FFT[J]. Acta Electronica Sinica, 2004,32(4):625-629.

[5] Rife D C, Vincent G A. Use of the discrete Fourier transform in the measurement of frequencies and levels of tones[J]. Bell System Technical Journal,1970,49:197-228.

[6] Jane V K, Collins W L, Davis D C. High accuracy analog measurements via interpolated FFT[J]. IEEE Trans IM, 1979,28(2):113-122.

[7] Quinn B G. Estimating frequency by interpolation using fourier coefficients[J]. IEEE Trans Signal Process,1994,42(5):1264-1268.

[8] Aboutanios E, Mulgrew B. Iterative frequency estimation by interpolation on fourier coefficients[J].IEEE Trans Signal Process,2005,53(4):1237-1242.

[9] 周龙健,罗景青,房明星. 基于IIN算法和Rife算法的正弦波频率估计算法[J].数据采集与处理,2013,28(6):839-842.

Zhou Longjian, Luo Jingqing, Fang Mingxing. Frequency estimation of sinusoid wave based on IIN algorithm and rife algorithm[J]. Journal of Data Acquisition and Processing, 2013,28(6):839-842.

[10]陈兵，祝俊，唐斌. 修正傅立叶系数插值测频算法及DSP实现[J].信号处理，2009,25(2):285-288.

Chen Bing, Zhu Jun, Tang Bin. Modified frequency estimator using Fourier coefficients interpolation and its DSP implementation[J]. Signal Processing, 2009,25(2):285-288.

[11]谢胜,陈行,于平,等. 基于Quinn算法和相位差法的正弦波频率估计综合算法[J]. 信号处理, 2011,27(5):771-775.

Xie Sheng, Chen Hang, Yu Ping, et al. Sinusoid wave frequency estimation combined algorithm based on Quinn algorithm and phase difference correction algorithm [J]. Signal Processing, 2011,27(5):771-775.

[12]王俊，刘红星. 基于插值Fast Fourier transform 谐波分析的桥梁状态评估方法[J].南京大学学报(自然科学版)，2009，45(4)：482-487.

Wang Jun, Liu Hongxing. A new technology to assess long-span bridge condition based on harmonic analysis via interpolated Fast Fourier transform[J].Journal of Nanjing University:Natural Sciences, 2009,45(4):482-487.

[13]孟建. 相参信号频谱的精确估计[J].系统工程与电子技术,1999,21(10): 67-70.

Meng Jian. Spectrum estimating of correlative signal[J]. Systems Engineering and Electronics,1999,21(10):67-70.

[14]林云松, 黄勇, 肖先赐. 实正弦信号的快速相位差分频率估计方法[J].电子科技大学学报, 1999,8(2):120-123.

Lin Yunsong, Huang Yong, Xiao Xianci. Fast frequency estimation methods o f real sinusoidal signal from phase differences[J].Journal of University of Electronic Science and Technology of China,1999,8(2):120-123.

[15]丁康，张晓飞. 频谱校正理论的发展[J].振动工程学报,2000,13(1):15-22.

Ding Kang, Zhang Xiaofei. Advances in spectrum correction theory[J]. Journal of Vibration Engineering, 2000,13(1):15-22.

This paper proposes an improved frequency estimation algorithm using discrete Fourier transform (DFT) interpolation based on the Quinn algorithm and iterative interpolation algorithm (A&M algorithm). The proposed algorithm first uses a frequency error estimated by the Quinn algorithm as the initial error value of the iterative estimation algorithm. Then frequency error is estimated accurately by the iteration algorithm. The algorithm can effectively reduce the number of iterations and guarantee the precision of estimation results, thus improving the computational efficiency. To enhance the efficiency of the algorithm on the DSP processor, this paper also proposes an optimization method for the implementation of the algorithm on the DSP processor, which is helpful for the application of the algorithm in real time. The simulation results show that the proposed algorithm can increase the frequency estimation accuracy, and the efficiency of real-time computation with good anti-noise performance.

frequency estimation; discrete Fourier transform(DFT) interpolation; estimation precision

国家自然科学基金(61601206)资助项目;江苏省自然科学基金(BK20160565)资助项目;江苏省高校自然科学研究(15KJB310003)资助项目。

2014-07-22；

2014-09-29

TP391

A

郑威(1982-)，男，博士，讲师，研究方向：生物医学信息检测与处理，E-mail:zhweiweixy@gmail.com。

陈德昶(1990-)，男，硕士研究生，研究方向:数据采集与处理、DSP实现。

刘红星(1968-)，男，教授，研究方向：智能信号处理、生物医学信号处理。

Improved Frequency Estimation Algorithm Using DFT Interpolation and Its Implementation on DSP

Zheng Wei1, Chen Dechang1, Liu Hongxing2

(1.College of Electronic Information, Jiangsu University of Science and Technology, Zhenjiang, 212003, China; 2.College of Electronic Science and Engineering, Nanjing University, Nanjing, 210093, China)