基于随机游走的流形学习与可视化

邵 超 万春红 张啸剑

(河南财经政法大学计算机与信息工程学院,郑州，450046)

基于随机游走的流形学习与可视化

邵 超 万春红 张啸剑

(河南财经政法大学计算机与信息工程学院,郑州，450046)

现有的全局流形学习算法都敏感于邻域大小这一难以高效选取的参数,它们都采用了基于欧氏距离的邻域图创建方法,从而使邻域图容易产生“短路”边。本文提出了一种基于随机游走模型的全局流形学习算法(Random walk-based isometric mapping，RW-ISOMAP)。和欧氏距离相比,由随机游走模型得到的通勤时间距离是由给定两点间的所有通路以概率为权组合而成的,不但鲁棒性更高,而且还能在一定程度上度量具有非线性几何结构的数据之间的相似性。因此采用通勤时间距离来创建邻域图的RW-ISOMAP算法将不再敏感于邻域大小参数,从而可以更容易地选取邻域大小参数,同时还具有更高的鲁棒性。最后的实验结果证实了该算法的有效性。

全局流形学习;等距映射;邻域图;随机游走;通勤时间距离

引 言

随着大数据时代的到来,人们越来越重视通过维数约简方法来获得高维数据的低维简洁表示,这样可以极大地提高数据洞察力。近年来,人们提出了多种流形学习算法,可以发现很多高维非线性数据内在的低维流形,成为目前比较有效的非线性维数约简方法[1],如典型的全局流形学习算法等距映射[2-4](Isometric mapping,ISOMAP)和典型的局部流形学习算法局部线性嵌入[5-6](Locally linear embedding,LLE)等。其中,以等距映射为代表的一类流形学习算法通过保持数据点之间的全局度量如测地距离来获得数据的低维嵌入,从而能更好地保持数据的全局结构、获得更好的可视化结果,称为全局流形学习算法。这些全局流形学习算法都敏感于邻域大小这一实际中难以高效选取的参数[7-9]。究其主要原因,它们都采用了基于欧氏距离的邻域图创建方法,容易在邻域图中产生“短路”边,从而使这些全局流形学习算法都敏感于邻域大小参数和数据中的噪声,鲁棒性较低。目前人们大都采用欧氏距离来创建邻域图,主要有K-最近邻(K-nearest neighbor，KNN)法和ε-邻域(ε-neighborhood)法等。为使邻域图能正确反映数据的内在几何结构,从而成功运行流形学习算法,人们通常使用残差来选取合适的邻域大小参数[2,10],但需要多次运行整个流形学习算法,从而使该参数在实际中难以高效选取。通过对多个运行结果进行集成[8],可以减弱邻域大小参数对流形学习算法的影响,但时间复杂度会明显增大。通过剔除邻域图中的“短路”边[11-12],也可以减弱邻域大小参数对流形学习算法的影响,但同时又会引入新的同样难以高效选取的额外参数。文献[13,14]为每一个数据点自适应地选取不同的邻域大小参数,但计算相对复杂。

近年来,人们利用随机游走(Random walk)理论,在邻域图上得到了通勤时间距离[15-18]这一新型的距离度量,它由邻域图上给定两点间的所有通路以概率为权组合而成。因此,和ISOMAP算法采用的单一最短路径距离相比,通勤时间距离更加鲁棒;和创建邻域图常用的欧氏距离相比,通勤时间距离能在一定程度上度量具有非线性几何结构的数据之间的相似性[15-18]。因此,采用通勤时间距离来创建邻域图不但能更好地避免“短路”边,减弱邻域大小参数对流形学习算法的影响,从而更容易地选取邻域大小参数,而且还能使流形学习算法获得更高的鲁棒性,这就是本文算法的出发点。

1 随机游走模型和通勤时间距离

数据分析首先需要计算任意两个数据点之间的相似度,通常采用

(1)

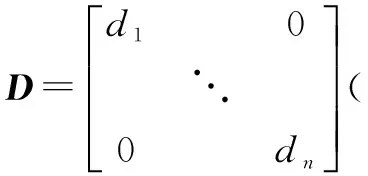
(2)

该度量将邻域图上从xi到xj的所有通路以概率为权进行组合,不但能在一定程度上度量具有非线性几何结构的数据之间的相似性[15-18](据此创建的邻域图不容易产生“短路”边,因此对邻域大小参数并不敏感),而且比单一的最短路径距离更加鲁棒,但它并不对称,经对称化后为通勤时间距离[15-16]，则

c(i,j)=h(i|j)+h(j|i)

(3)

经证明,通勤时间距离可以根据式(4)计算得到[15,16]，则

(4)

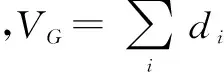
(5)

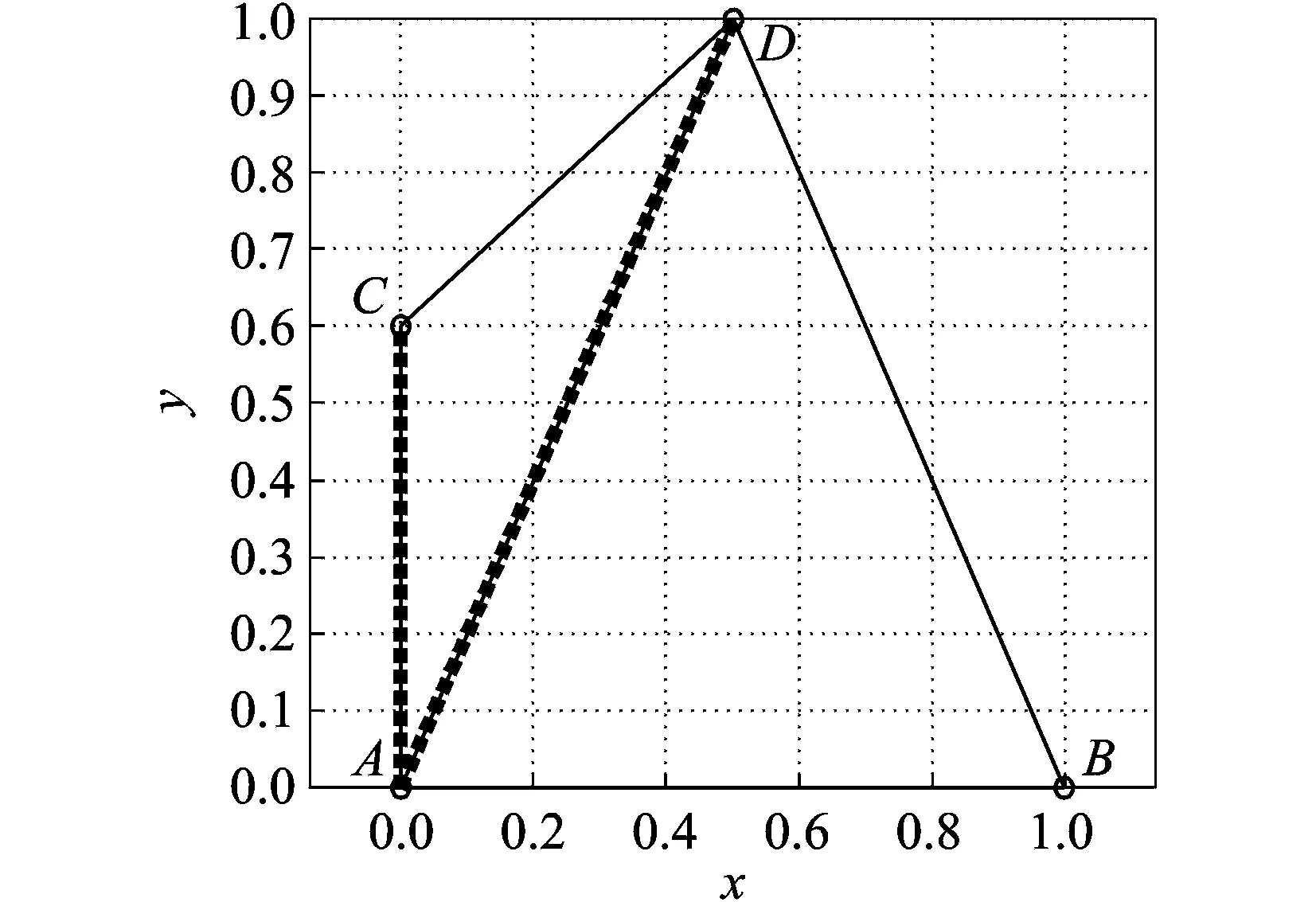
图1 数据集{A,B,C,D}的邻域图(k=2)Fig.1 Neighborhood graph of data set {A,B,C,D}(k=2)

式中：Λ为包含L+最大几个(为了数据可视化,通常为2或3)特征值的对角矩阵,Φ为对应的特征向量矩阵。给定两点间的通路越多,或某些通路越短,其通勤时间距离就会越小[15-18](如图1所示)。因此,CTE算法会扭曲数据的全局几何结构(见随后的实验结果)。另外,基于通勤时间距离来创建的邻域图可能会漏掉其中某些最近邻点(如图1所示,如果采用通勤时间距离,数据点B就不再是A的k-最近邻点(k=2)),从而难以确保最短路径距离对测地距离这一全局度量的良好逼近[2]。在图1中，数据集{A，B，C，D}的邻域图(k=2)，如细实线表示,其中,数据点A的两个k-最近邻点为B和C。然而,如果采用通勤时间距离,则数据点A的两个k-最近邻点不再是B和C,而是C和D,如粗虚线表示,这是因为D和A之间存在多条相对较短的通路,如(A,D)和(A,C,D)。

2 RW-ISOMAP算法

为了更好地展现数据的全局几何结构,本文依然采用ISOMAP算法的做法,即在低维嵌入空间中保持由最短路径距离逼近得到的流形上唯一有意义的全局度量—测地距离;但不同之处在于本文采用随机游走模型得到的通勤时间距离来创建邻域图,以此来减弱邻域大小参数对流形学习算法的影响,并提高流形学习算法的鲁棒性。为了确保对测地距离的良好逼近,首先应为每个数据点都保留若干个最近邻点,同时为了能在最大程度上避免“短路”边,本文采用使邻域图能够连通的最小k值(记作km)来创建邻域图(称为最小连通邻域图,记作Gm)。然后在最小连通邻域图的基础上使用通勤时间距离来为每个数据点增加更多的最近邻点。由于通勤时间距离考虑了数据内在的非线性几何结构,能在避免“短路”边的情况下使邻域图足够稠密,从而使测地距离能够得到更加精确的逼近[19]。因此本文算法基于随机游走模型的全局流形学习算法(Random walk-based ISOMAP，RW-ISOMAP)可简要描述为

(1)给定数据集X=(xi)，i=1,…,n,采用欧氏距离来创建最小连通邻域图Gm:

(a)k=0;

(b) Do

(i)k=k+1;

(ii) 采用k-最近邻法创建邻域图G;

(iii) 在G上运行广度优先搜索算法判断其是否连通;

(c) UntilG连通;

(d)Gm=G;km=k。

(2)计算任一数据点xi基于通勤时间距离的k-最近邻点集合N'k(i):

(a) 给定邻域大小参数k1,根据式(1)计算相似矩阵W=(wij)n×n;

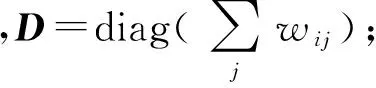
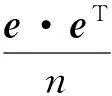
(d) 根据式(4)计算所有数据点之间的通勤时间距离C=(c(i,j))n×n;

(e) 计算xi基于通勤时间距离的k-最近邻点集合N'k(i)={j|j≠i∧IND(c(i,j))≤k}(和基于欧氏距离的k-最近邻点集合Nk(i)不同),其中,k为邻域大小参数,IND(c(i,j))为c(i,j)在c(i,·)(除c(i,i)外)升序排列中的次序。

(3)给定邻域大小参数k2,对于任一xi,如果j∈N'k2(i),则将连接边加入到邻域图Gm中,最终得到邻域图G。

(4)在G上计算所有的最短路径距离(同ISOMAP算法)。

(5)运行古典多维尺度分析(Classical multi-dimensional scaling,CMDS)算法,得到所有数据点的低维嵌入(同ISOMAP算法)。如上所述,RW-ISOMAP算法主要有3个参数:k1,k2和t。其中,邻域大小参数k1和尺度参数t用于在式(1)中计算通勤时间距离。由于通勤时间距离以概率为权对给定两点间的所有通路进行加权和,转移概率相对较小且稀疏得多的“短路”边对通勤时间距离的影响会比较小(如图2所示,当k1取不同值(如k1=8，16，24)时,基于通勤时间距离的CTE算法其结果几乎相同),从而使RW-ISOMAP算法对k1并不敏感。图2所用算法为CTE,数据集为Swiss roll(如图3(a)所示)。

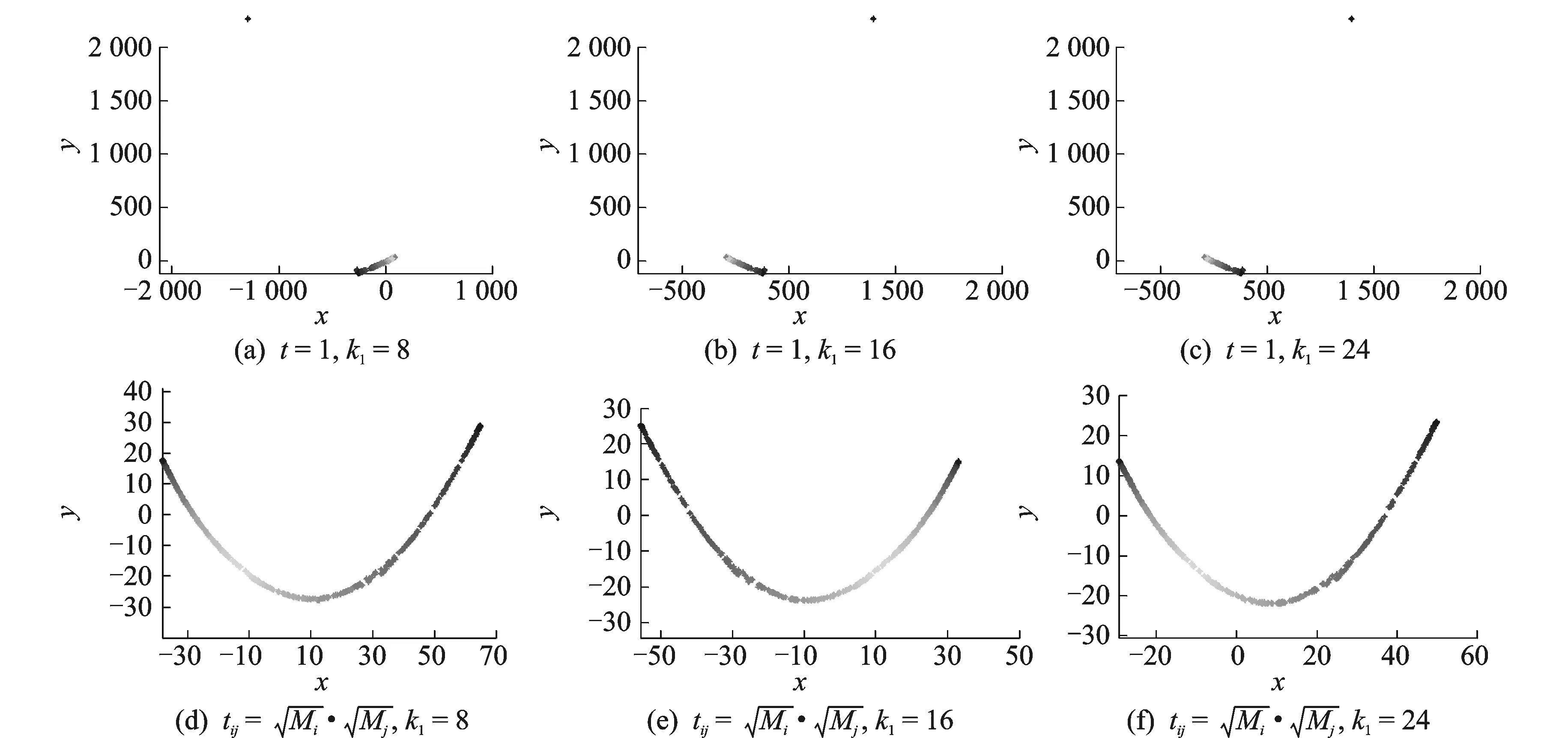
图2 参数t对可视化结果的影响Fig.2 Influence of parameter t on visualization results

稀疏得多的“短路”边通常都是长边,为了给长边的两个顶点赋予更小的相似度(使其具有更小的转移概率,这样可以进一步降低“短路”边对通勤时间距离的不良影响),尺度参数t通常取比较小的值,如t=1。为了更好地对分布不均匀的数据进行可视化,RW-ISOMAP算法采用保角等距映射[20](Conformal ISOMAP，C-ISOMAP)算法的作法,即

(6)

式中：xip和xjp分别为xi和xj的第p个k-最近邻点。该方法得到的可视化结果如图2(d-f)所示。和图2(a-c)相比,给不同的连接边赋予不同的参数tij能够得到更好的可视化结果。因此随后实验中的CTE算法也将采用这一方法。邻域大小参数k2用于在最小连通邻域图Gm上加入更多的连接边,由于通勤时间距离能够在一定程度上度量具有非线性几何结构的数据之间的相似性(如图4(d-f)所示,在流形上相距较远的数据点,其通勤时间距离也比较大),采用通勤时间距离来创建邻域图不容易产生“短路”边,从而使RW-ISOMAP算法对k2也不敏感。

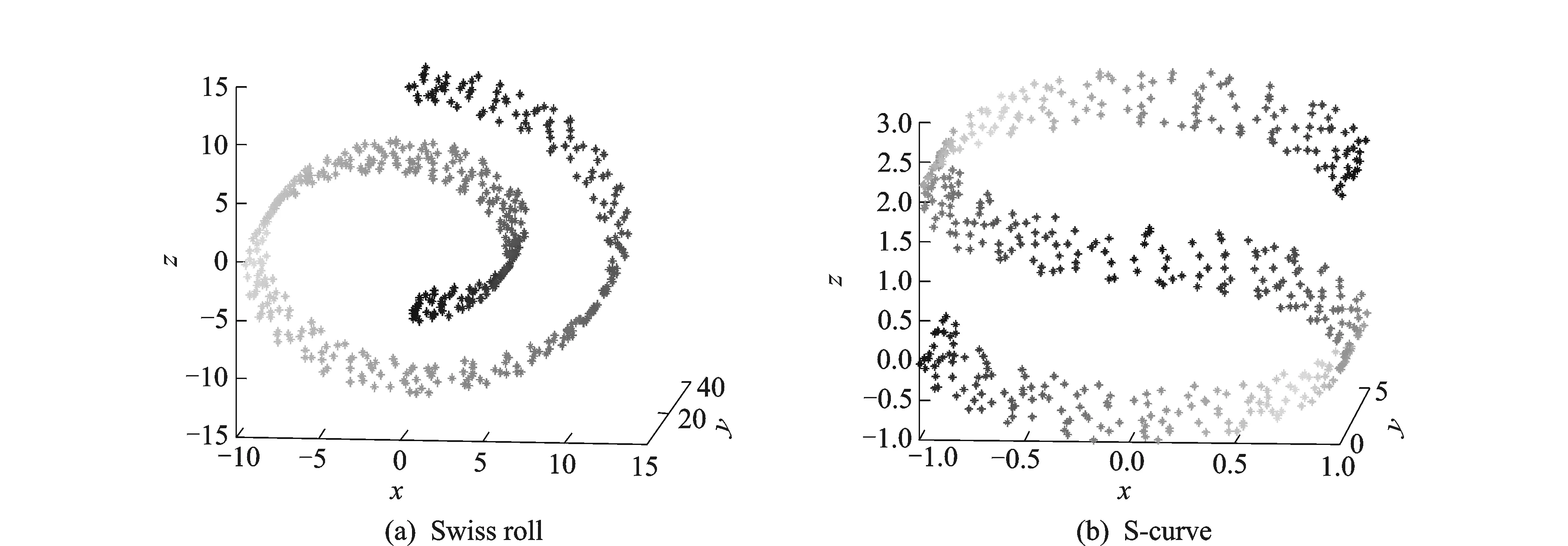
图3 实验中的两个数据集Fig.3 Two data sets in experiments

3 实验结果

3.1 完整流形的实验结果

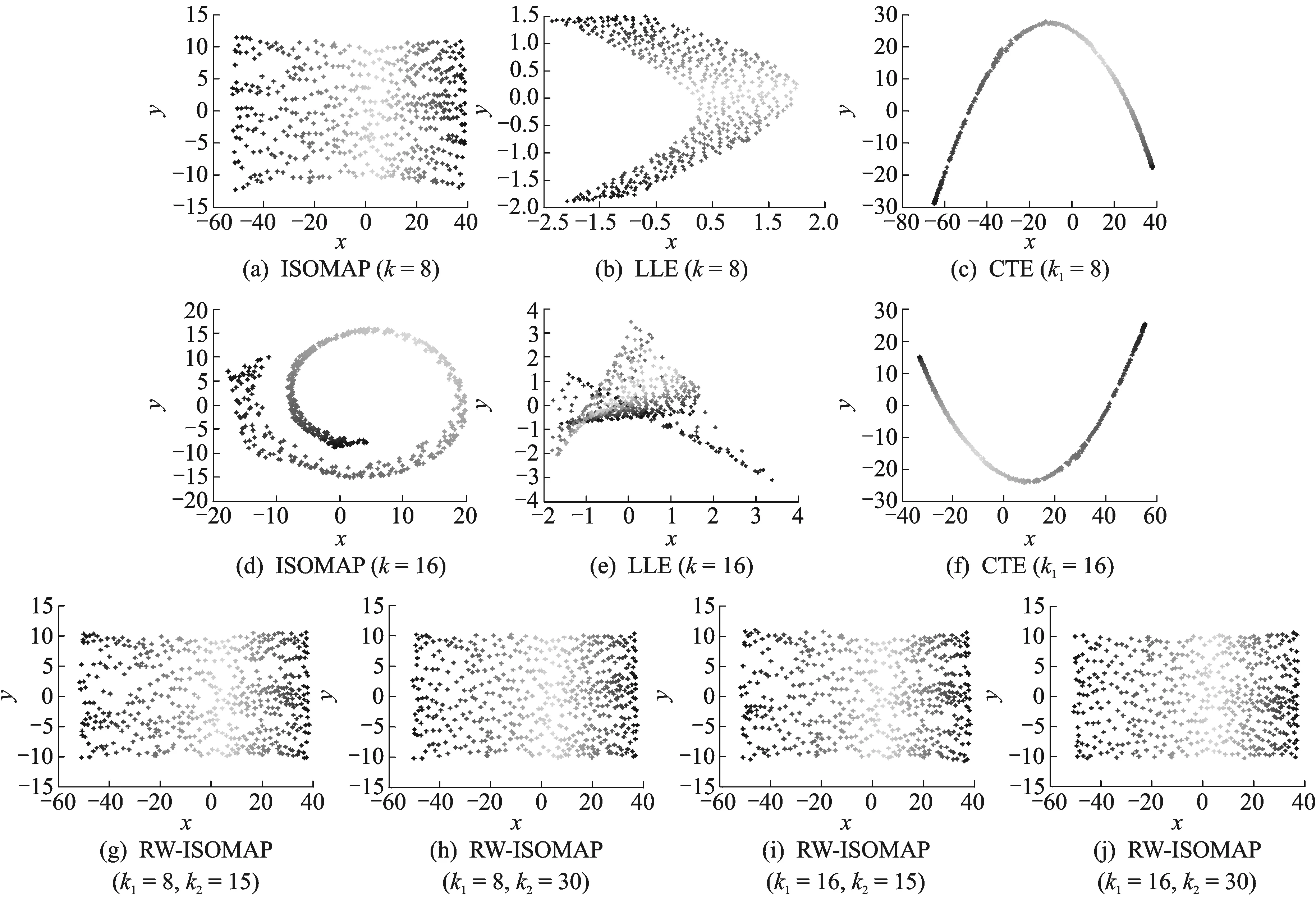
图4 不同算法对Swiss roll的可视化结果Fig.4 Visualization results of different algorithms on Swiss roll

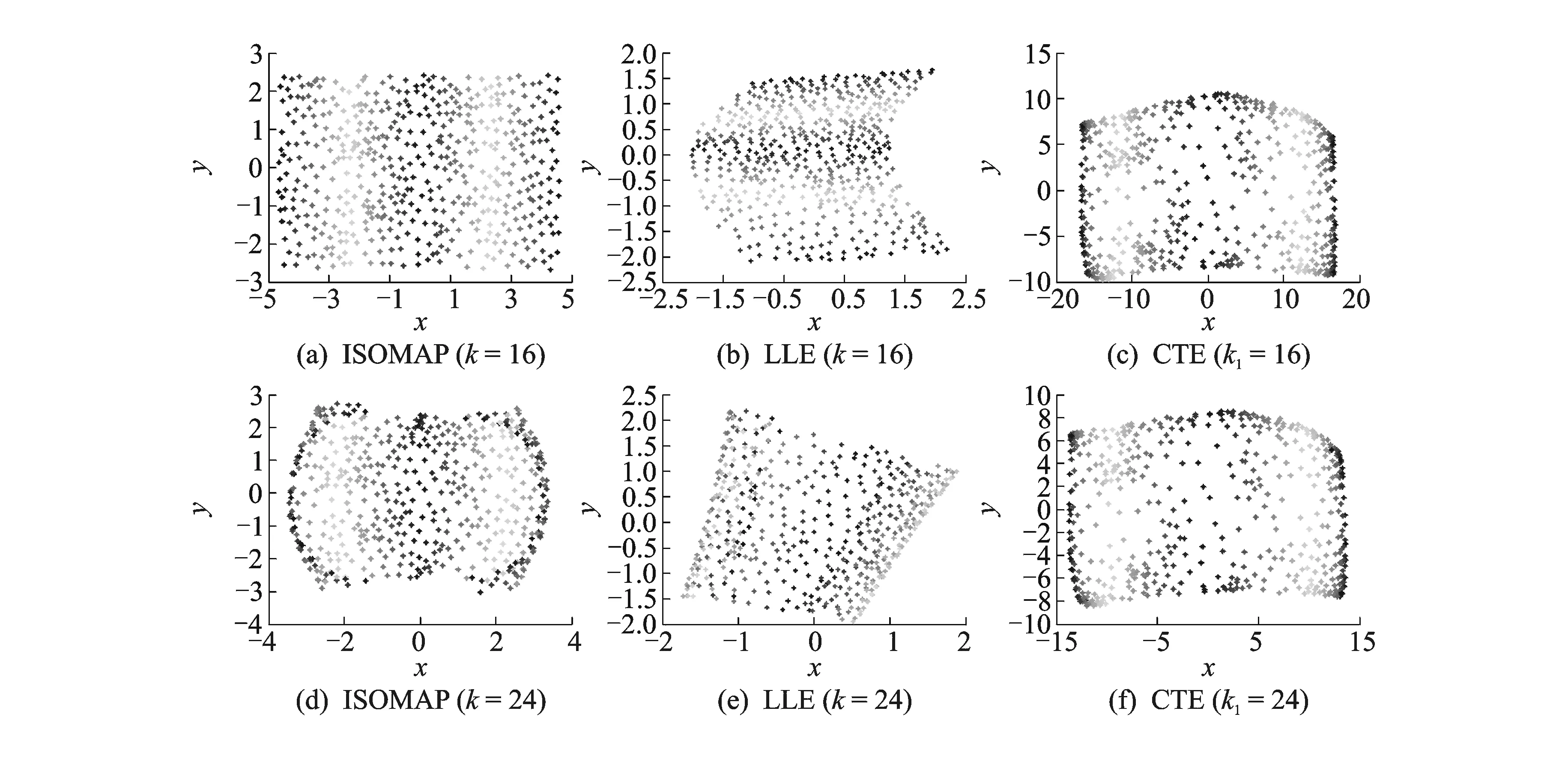
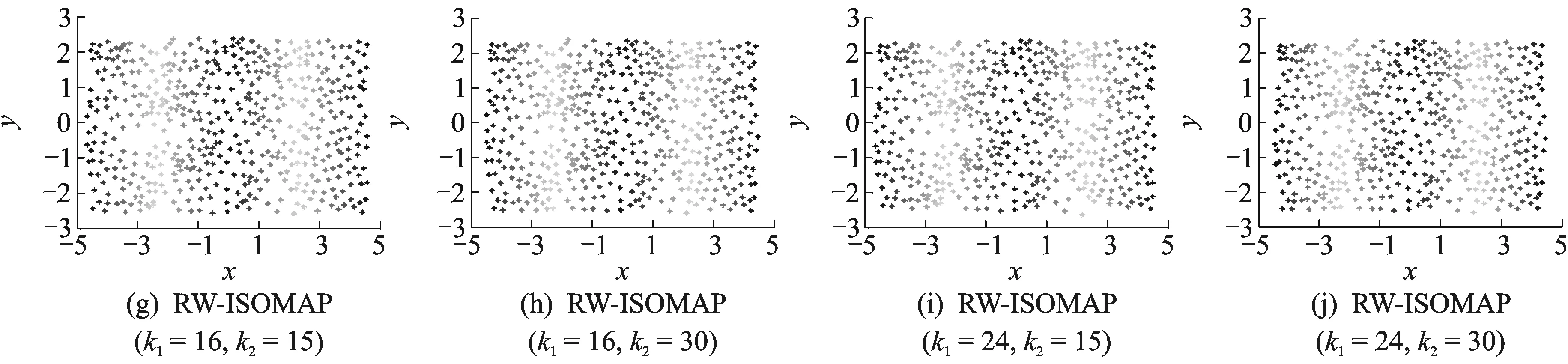
图5 不同算法对S-curve的可视化结果Fig.5 Visualization results of different algorithms on S-curve

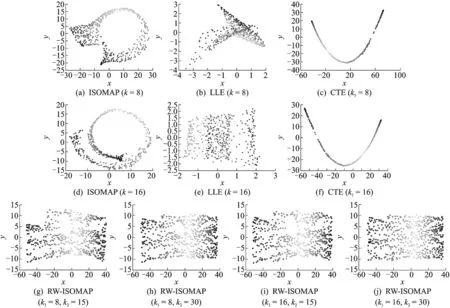
图6 不同算法对加入了噪声的Swiss roll的可视化结果Fig.6 Visualization results of different algorithms on Swiss roll with noise

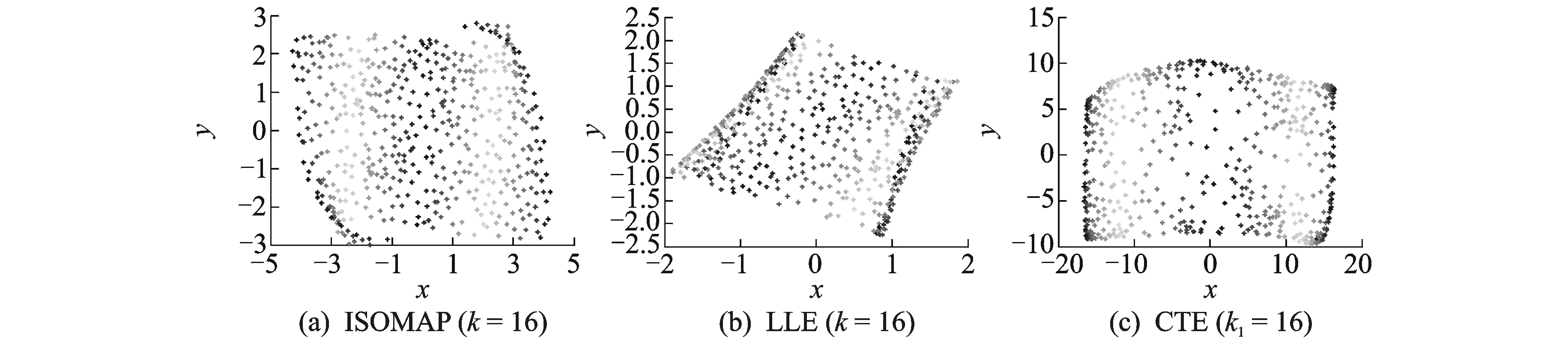
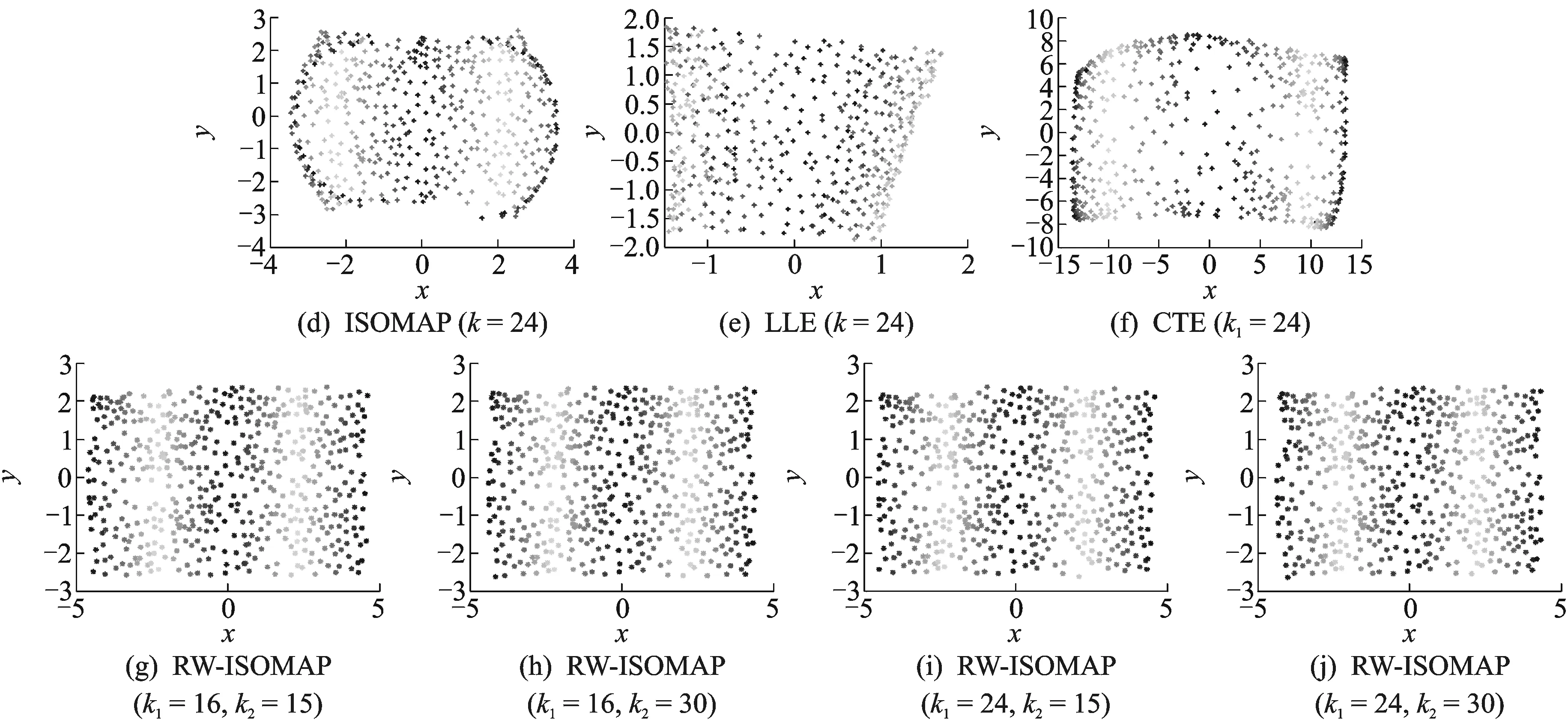
图7 不同算法对加入了噪声的S-curve的可视化结果Fig.7 Visualization results of different algorithms on S-curve with noise

为了验证本文提出的RW-ISOMAP算法的有效性,本文在Swiss roll[2]和S-curve[5]数据集(具有500个数据点,如图3所示)上分别运行ISOMAP，LLE，CTE和RW-ISOMAP算法,实验结果分别如图4，5所示。如图4(a，b,d，e)和图5(a，b,d，e)所示,当邻域大小参数合适时,如k=8(Swiss roll)和k=16(S-curve),ISOMAP和LLE算法都能较好地展现数据的内在几何结构,然而，当邻域大小参数取更大值时，如k=16(Swiss roll)和k=24(S-curve)，ISOMAP算法和LLE算法会扭曲数据的内在几何结构，相比之下,CTE算法能较好地展现数据的内在几何结构,但会扭曲数据的全局几何结构,如图4(c,f)和图5(c,f)所示。如图4(g-j)和图5(g-j)所示,和ISOMAP，LLE算法相比,RW-ISOMAP算法并不敏感于它的两个邻域大小参数k1和k2。和LLE，CTE算法相比,RW-ISOMAP算法能更好地展现数据的全局几何结构,这是因为RW-ISOMAP算法保持的也是测地距离这一全局度量,而不是和通路条数相关的通勤时间距离。为了验证RW-ISOMAP算法的鲁棒性,本文在这两个数据集上分别加入了一定程度的噪声[21],并再次运行ISOMAP算法、LLE算法、CTE算法和RW-ISOMAP算法,实验结果分别如图6，7所示。如图6(a-c)和图7(a-c)所示,在加入了噪声的这两个数据集上,ISOMAP和LLE算法已经不能正确地展现数据的内在几何结构,而CTE算法却依然能较好地展现数据的内在几何结构,从而具有一定的鲁棒性。相比之下,如图6(g-j)和图7(g-j)所示,在加入了噪声的这两个数据集上,RW-ISOMAP算法依然能较好地展现数据的内在几何结构,不但具有和CTE算法(如图6(c,f)和图6(c,f)所示)相当的鲁棒性,而且具有更好的全局保持能力。众所周知,残差可用来衡量低维嵌入映射的质量,进而用来判断流形学习算法对邻域大小参数的敏感程度。如图8所示,RW-ISOMAP和CTE算法对邻域大小参数的敏感程度远低于ISOMAP和LLE算法。此外RW-ISOMAP算法得到的映射质量要远好于CTE算法(表现为更小的残差)。

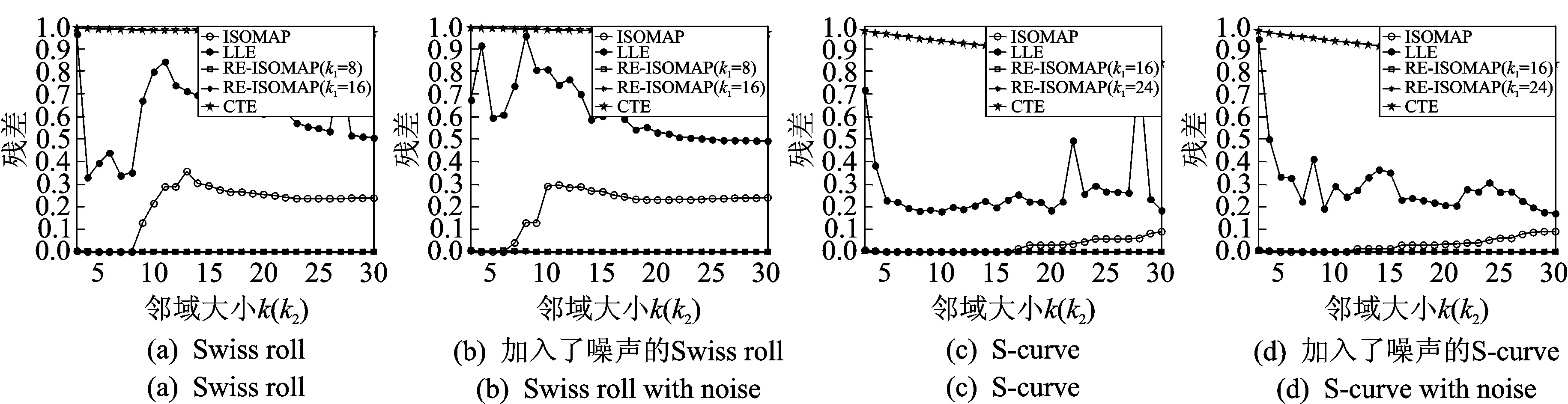
图8 不同算法得到的残差Fig.8 Residual variances obtained by different algorithms on different data sets

3.2 不完整流形的实验结果

为了验证RW-ISOMAP算法在不完整流形上的有效性,本文在Swiss roll数据集上去掉一些数据点形成一个空洞(如图9所示),再次运行ISOMAP算法、LLE算法、CTE算法和RW-ISOMAP算法,实验结果如图10所示,RW-ISOMAP算法不但能较好地展现该数据的内在几何结构(ISOMAP算法只有在邻域大小参数合适时才能做到这一点),而且对邻域大小参数也不敏感。

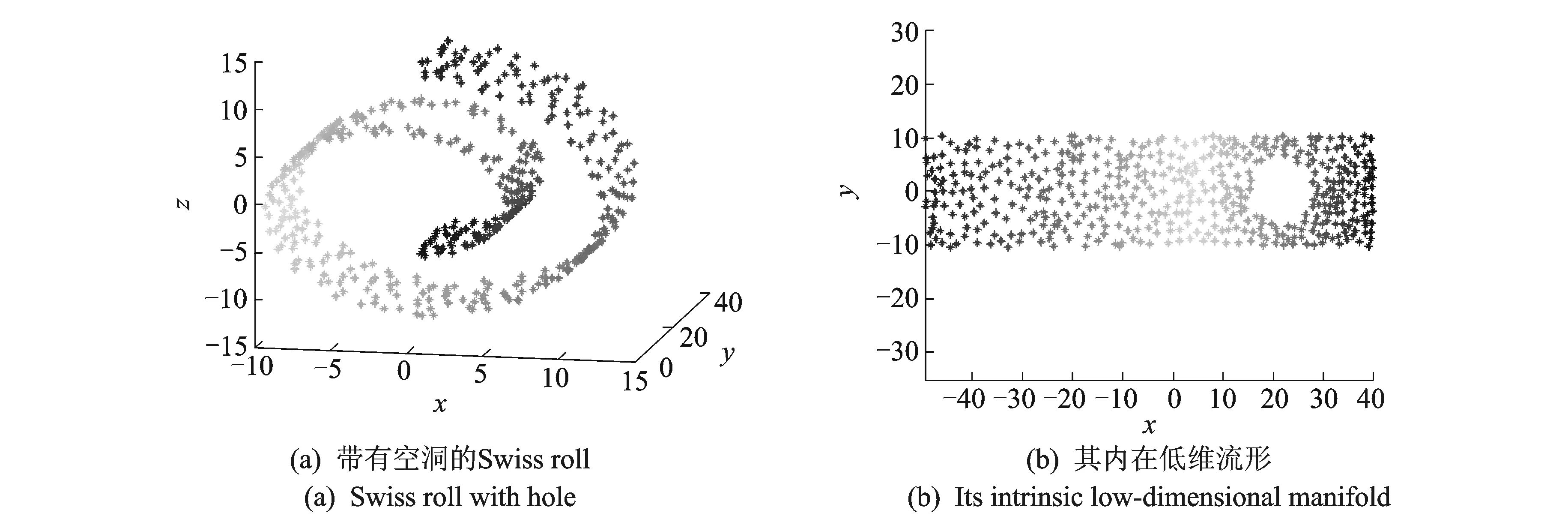
图9 带有空洞的Swiss roll及其内在低维流形Fig.9 Swiss roll data set with hole and its intrinsic low-dimensional mailfold

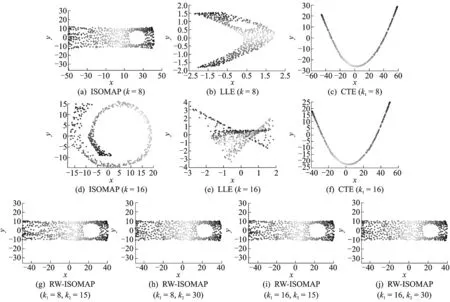
图10 不同算法对带有空洞的Swiss roll的可视化结果Fig.10 Visualization results of different algorithms on Swiss roll with hole

3.3 实际数据集的实验结果

为了验证RW-ISOMAP算法在实际数据集上的有效性,本文在人脸数据集[2]上再次运行ISOMAP算法、LLE算法、CTE算法和RW-ISOMAP算法。如图11所示,RW-ISOMAP和CTE算法对邻域大小参数的敏感程度依然低于ISOMAP和LLE算法。给定邻域大小参数k=k1=k2=10(比最大合适邻域大小k=8(如图11所示)稍大),图11由该邻域大小参数在ISOMAP，LLE和CTE这3个算法中为k,而在RW-ISOMAP算法中为k2。RW-ISOMAP算法依然能获得人脸图像的有意义排列(如图12所示)。

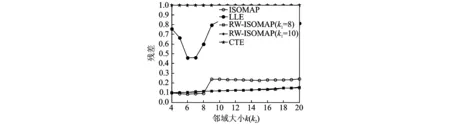
图11 不同算法在人脸数据集上得到的残差Fig.11 Residual variances obtained by different algorithms on face data set

4 结束语

由随机游走模型得到的通勤时间距离具有良好的鲁棒性,且考虑了数据内在的非线性几何结构,因此本文提出了基于随机游走的全局流形学习算法RW-ISOMAP,以克服传统的基于欧氏距离的邻域图创建方法鲁棒性差、拓扑不稳定等问题。该算法在最小连通邻域图的基础上加入更多的基于通勤时间距离的连接边,从而能在避免“短路”边的前提下使邻域图足够稠密,以实现对测地距离的良好逼近。因此该算法不但能真实地展现数据的全局几何结构,而且具有较高的鲁棒性。如何将该算法扩展至多流形数据将是下一步的研究内容。

[1] 杨剑,李伏欣,王珏.一种改进的局部切空间排列算法[J].软件学报,2005,16(9):1584-1590.

Yang Jian, Li Fuxin, Wang Jue. A better scaled local tangent space alignment algorithm[J]. Journal of Software,2005,16(9):1584-1590.

[2] Tenenbaum J B, de Silva V, Langford J C. A global geometric framework for nonlinear dimensionality reduction[J].Science,2000,290(5500):2319-2323.

[3] 王耀南,张莹,李春生.基于核矩阵的ISOMAP增量学习算法研究[J].计算机研究与发展,2009,46(9):1515-1522.

Wang Yaonan, Zhang Ying, Li Chunsheng. Kernel matrix based incremental learning isomap algorithm[J].Journal of Computer Research and Development,2009,46(9):1515-1522.

[4] 吴文通,李元祥,韦邦合,等.局部测地距离估计的增量等距特征映射算法[J].上海交通大学学报,2013,47(7):1082-1086.

Wu Wentong, Li Yuanxiang, Wei Banghe, et al. Incremental ISOMAP method based on locally estimated geodesic distance[J].Journal of Shanghai Jiaotong University,2013,47(7):1082-1086.

[5] Roweis S T, Saul L K. Nonlinear dimensionality reduction by locally linear embedding[J].Science,2000,290(5500):2323-2326.

[6] Zhang S. Enhanced supervised locally linear embedding[J].Pattern Recognition Letters,2009,30(13):1208-1218.

[7] Saul L K, Roweis S T. Think globally, fit locally: Unsupervised learning of low dimensional manifolds[J].Journal of Machine Learning Research,2003,4(1):119-155.

[8] 詹德川,周志华.基于集成的流形学习可视化[J].计算机研究与发展,2005,42(9):1533-1537.

Zhan Dechuan, Zhou Zhihua. Ensemble based manifold learning for visualization[J].Journal of Computer Research and Development,2005,42(9):1533-1537.

[9] 邵超,黄厚宽,赵连伟.一种更具拓扑稳定性的ISOMAP算法[J].软件学报,2007,18(4):869-877.

Shao Chao, Huang Houkuan, Zhao Lianwei. A more topologically stable ISOMAP algorithm[J].Journal of Software,2007,18(4):869-877.

[10]Samko O, Marshall A D, Rosin P L. Selection of the optimal parameter value for the ISOMAP algorithm[J].Pattern Recognition Letters,2006,27(1):968-979.

[11]Wen G, Jiang L, Shadbolt N R. Using graph algebra to optimize neighborhood for isometric mapping[C]∥Veloso M M.Proceedings of the 20th International Joint Conference on Artificial Intelligence.Menlo Park,CA:AAAI Press,2007:2398-2403.

[12]Yang L. Building k edge-disjoint spanning trees of minimum total length for isometric data embedding[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,2005,27(10):1680-1683.

[13]文贵华,江丽君,文军.邻域参数动态变化的局部线性嵌入[J].软件学报,2008,19(7):1666-1673.

Wen Guihua, Jiang Lijun, Wen Jun. Dynamically determining neighborhood parameter for locally linear embedding[J].Journal of Software,2008,19(7):1666-1673.

[14]Zhang Z, Wang J, Zha H. Adaptive manifold learning[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,2012,34(2):1473-1480.

[15]Qiu H, Hancock E R. Clustering and embedding using commute times[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,2007,29(11):1873-1890.

[16]Fouss F, Pirotte A, Renders J M, et al. Random-walk computation of similarities between nodes of a graph with application to collaborative recommendation[J].IEEE Transactions on Knowledge and Data Engineering,2007,19(3):355-369.

[17]Albano J A, Messinger D W. Euclidean commute time distance embedding and its application to spectral anomaly detection[C]∥Proceedings of SPIE 8390.Bellingham,WA:SPIE,2012:1-15.

[18]Kim K H, Choi S. Walking on minimax paths for k-NN search[C]∥Proceedings of the 27th AAAI Conference on Artificial Intelligence. Bellevue,Washington,USA:AAAI Press,2013:518-525.

[19]Jing L, Shao C. Selection of the suitable parameter value for ISOMAP[J].Journal of Software,2011,6(6):1034-1041.

[20]de Silva V, Tenenbaum J B. Global versus local methods in nonlinear dimensionality reduction[J].Advances in Neural Information Processing Systems,2003,15:721-728.

[21]Balasubramanian M, Shwartz E L, Tenenbaum J B, et al. The ISOMAP algorithm and topological stability[J].Science,2002,295(5552):7.

The existing global manifold learning algorithms are relatively sensitive to the neighborhood size, which is difficult to select efficiently. The reason is mainly because the neighborhood graph is constructed based on Euclidean distance, by which shortcut edges tend to be introduced into the neighborhood graph. To overcome this problem, a global manifold learning algorithm is proposed based on random walk, called the random walk-based isometric mapping (RW-ISOMAP). Compared with Euclidean distance, the commute time distance, achieved by the random walk on the neighborhood graph, can measure the similarity between the given data within the nonlinear geometric structure to a certain extent, thus it can provide robust results and is more suitable to construct the neighborhood graph. Consequently, by constructing the neighborhood graph based on the commute time distance, RW-ISOMAP is less sensitive to the neighborhood size and more robust than the existing global manifold learning algorithms. Finally, the experiment verifies the effectiveness of RW-ISOMAP.

global manifold learning; isometric mapping; neighborhood graph; random walk; commute time distance

国家自然科学基金(61202285)资助项目；河南省教育厅科学技术研究重点(14B520020)资助项目。

2015-06-03；

2015-06-30

TP181

A

邵超(1977-),男,博士,教授,硕士生导师,研究方向：机器学习、数据挖掘与可视化,E-mail：sc_flying@163.com。

万春红(1982-),女,讲师,研究方向：机器翻译与自然语言处理。

张啸剑(1980-),男,博士,副教授,研究方向：数据挖掘、图数据管理与隐私保护。

Manifold Learning and Visualization Based on Random Walk

Shao Chao, Wan Chunhong, Zhang Xiaojian

(School of Computer and Information Engineering, Henan University of Economics and Law, Zhengzhou, 450046, China)