基于MapReduce框架的分布式软K段主曲线算法

胡作梁 张红云

(1.同济大学计算机科学与技术系，上海，201804；2.同济大学嵌入式系统与服务计算教育部重点实验室，上海，201804)

基于MapReduce框架的分布式软K段主曲线算法

胡作梁1,2张红云1,2

(1.同济大学计算机科学与技术系，上海，201804；2.同济大学嵌入式系统与服务计算教育部重点实验室，上海，201804)

传统的主曲线算法在小规模数据集上能获得良好的效果，但单节点的计算和存储能力都不能满足海量数据主曲线的提取要求，而算法分布式并行化是目前解决该类问题最有效的途径之一。本文提出基于MapReduce框架的分布式软K段主曲线算法(Distributed soft k-segments principal curve,DisSKPC)。首先，基于分布式K-Means算法，采用递归粒化方法对数据集进行粒化，以确定粒的大小并保证粒中数据的关联性。然后调用软K段主曲线算法计算每个粒数据的局部主成分线段，并提出用噪声方差来消除在高密集、高曲率的数据区域可能产生的过拟合线段。最后借助哈密顿路径和贪婪算法连接这些局部主成分线段，形成一条通过数据云中间的最佳曲线。实验结果表明，本文所提出的DisSKPC算法具有良好的可行性和扩展性。

分布式并行化；主曲线；数据粒化;MapReduce

引 言

主曲线是第一主成分的非线性推广[1]，是一条通过数据分布的“中间”且满足自相合的无参数光滑曲线。主曲线学习的主要任务是研究如何从数据集中提取主曲线。在数据主曲线提取方面，Hastie T和Stuetzle W于1988年首次提出了(Hastie and stuetzle principal curve,HSPC)主曲线算法[2]。虽然HSPC主曲线可以较好地描述非线性数据，并且该曲线具有自相合以及无参数性等优点，但其仍然存在很多不足，如曲线的存在性至今未得到证明，同时还伴随着模型偏差、估计偏差和收敛性等问题。为了解决这些问题，文献[3]提出了BR主曲线，解决了闭HSPC主曲线由于曲率过大导致明显估计偏差的问题。针对模型偏差，文献[4]引入了半参数方法，重新定义基于混合模型的主曲线，解决了圆形和椭圆分布数据的模型偏差问题。针对存在性问题，文献[5]引入了有长度约束的主曲线概念，提出了多边形主曲线(Polygonal line principal curve,PLPC)算法，并从理论上证明主曲线的存在性。随着主曲线应用的不断深入，可以发现以上这些主曲线算法在处理具有自相交、分叉和环形分布特征的形态较复杂数据时，第一主成分作为初值已不再有效。针对这种情况，文献[6]提出一个接一个地发现主定向点并且有序连接它们来估算主曲线，提出了D主曲线算法。文献[7]采用逐渐合并局部第一主成分线来形成主曲线，给出了K段主曲线算法。文献[8]在K段主曲线算法基础上定义了点属于线的概率，提出了软K段主曲线(Soft k-segments principal curve,SKPC)算法。文献[9]用Delicado生成的主定位点作为初值，采用核光滑子进行曲线光滑，提出了一种自底向上的主曲线算法。文献[10]提出基于聚类的分段主曲线算法来提取字符数据主曲线。文献[11]将数据局部特征引入主曲线提取中，提出局部主曲线算法，以上这些算法解决了自相交、分叉和环形分布特征数据的主曲线提取问题。近几年，文献[12]提出了自适应约束K段主曲线算法来解决稀疏和不均匀分布数据主曲线提取问题。文献[13]提出基于黎曼距离的主曲线算法，该算法采用数据的黎曼距离,结合数据的分布密度来解决非恒定数据分布的主曲线提取问题，并用于划分高维数据空间。文献[14]提出局部主曲线与主曲面算法，该算法采用基于核密度函数和高斯混合模型的子空间约束均值漂移来解决具有回路、自相交和分支分布特点数据的主曲线与主曲面提取问题。文献[15]将粒计算思想应用于复杂形态数据主曲线提取，提出了用相关主曲线算法来解决从具有自相交，高弯曲和高分散等分布特征的复杂形态数据中提取主曲线的问题并加以应用。文献[16]将主曲线推广到粒主曲线, 对从大规模数据中提取主曲线做了初步探索。文献[17]针对文献[14]提出的子空间约束均值漂移算法(Subspace constrained mean shift,SCMS)在训练过程中不能加入新数据点的问题，提出了增长型SCMS算法，该算法预先在小样本集上使用SCMS训练主曲线，通过判断新的数据点与训练点集中点的相似关系来更新曲线。主曲线学习经过将近40年的发展，在小数据集上已获得良好的效果，但如今许多应用亟需计算海量数据的主曲线，传统主曲线算法的适用性和响应时间都难以满足。因此，需要研究一种可扩展的、能有效处理海量数据的主曲线方法。算法分布式并行化是目前处理海量数据最有效的方法之一[18]，而最流行的分布式计算框架是Google工程师Dean J等提出的MapReduce编程模型[19]。近几年来，MapReduce得到了大量商业机构和学术研究人员的关注。在工业界，Yahoo、Facebook、阿里和百度等大型互联网公司，纷纷将MapReduce用于自己的大数据业务上，处理诸如用户行为分析、日志分析和网页搜索等任务。学术界也掀起了学习研究使用MapReduee解决海量数据问题的热潮，文献[20-26]分别给出了几种针对不同场景和应用需求的基于MapReduee的分布式并行算法实现。

本文设计并实现了基于MapReduce的分布式软K段主曲线算法(Distributed soft k-segments principal curve,DisSKPC)。考虑到SKPC处理的数据块必须是空间上的连续区域且数量不能过多，首先基于分布式K-Means，采用递归粒化方法对数据集进行粒化，以确定粒的大小并保证粒中数据的关联性，将MapReduce分块处理思想转换成分粒处理。然后MapTask调用SKPC算法计算每个粒数据的局部主成分线段，并提出用噪声方差来消除在高密集、高曲率的数据区域可能产生的过拟合线段。最后ReduceTask将连接局部主成分线段的问题转化成求解一条最优哈密顿路径，采用贪婪算法求解，由此得到一条通过数据云中间的最佳曲线。

1 相关工作

主曲线概念由Trevor Hastie[2]在1984首次提出，他将主曲线定义成一条通过数据云中间且满足自相合的光滑曲线。

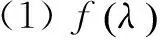
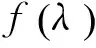
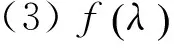
(1)

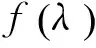
(2)

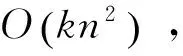
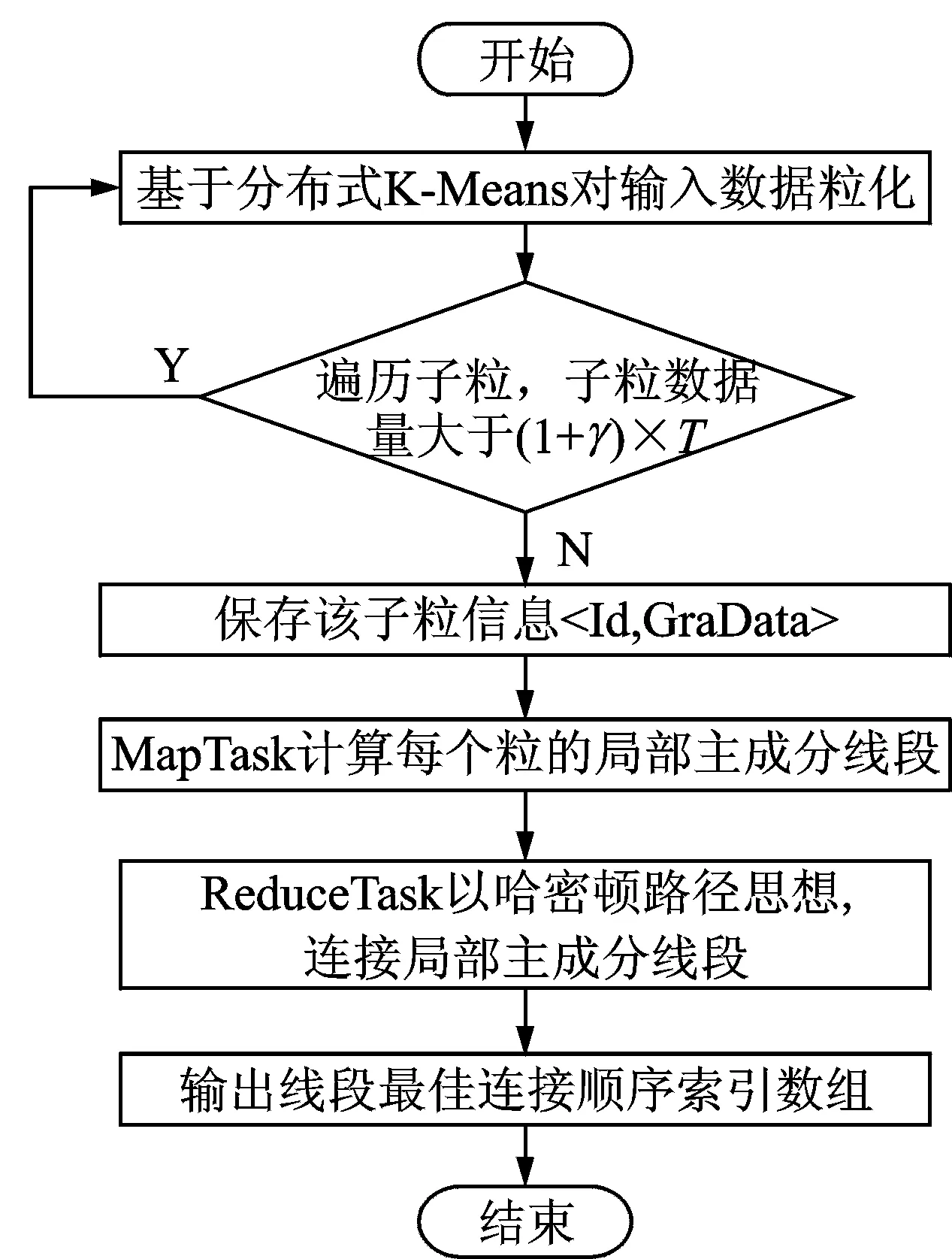
图1 DisSKPC算法流程Fig.1 DisSKPC flowchart

MapReduce最早是由Google提出的一种处理大规模数据集的分布式计算模型，模型的输入和输出均为键值对。MapReduce主要由Map和Reduce两个阶段构成，对需要处理海量数据的用户来说，分别编写函数Map和Reduce的业务逻辑就可以实现一个简单的分布式应用。Map函数：将输入Key/Value对按业务逻辑映射成另外一系列的Key/Vlaue对，并依据Key对中间数据对分组，结果传递给Reduce处理。Reduce函数：以组为单位对数据进行规约，并将最终产生的Key/Value对保存到输出文件中。

2 基于MapReduce的分布式SKPC算法DisSKPC

DisSKPC主要分为3个过程，分别是：(1) 对数据递归粒化，以确定粒的大小并保证粒中数据的关联性。(2) 执行Map操作，计算每个粒的局部主成分线段。(3) 执行Reduce操作，连接MapTask返回的局部主成分线段。图1为DisSKPC算法流程。MapReduce模型先对数据分块，然后并行处理每块数据，但默认的分块数据并不满足DisSKPC算法的要求。对于DisSKPC来说，每个数据块必须满足：(1) 每一块的数据在空间上是连续的区域，如果数据是空间上分散的区域，则Map会产生一系列随机、杂乱的线段。(2) 每一块的数据量不能过多，即单个高计算和存储消耗的SK算法不能处理过多的数据，以至于超过单个节点的计算和存储能力范围。所以，先将输入数据递归粒化，将分块处理转换成分粒处理。假设每个粒的数据量阈值为T，则初始粒个数为

(3)

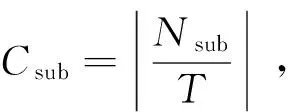
算法1RecurGraByDisKmeans

输入：输入数据Data、初始粒个数InitGraCount、粒总数TotoalGraCount、对子粒粒化标志Flag、粒化结果数组GraArray。

输出：粒化结果数组GraArray〈Id,GraData〉，Id为粒编号，GraData为该粒数据。

(1) 调用分布式K-Means算法对数据粒化，返回粒化结果。

(2) 计算粒化结果中每一粒的数据，输出〈Id,Data〉集合，Id为粒编号，Data为该粒数据。

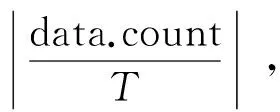
MapTask计算每个粒数据的局部主成分线段，输入为〈Id,GraData〉,Id为粒编号，GraData为粒数据，输出为〈Null,Lines〉,Lines为局部主成分线段端点坐标矩阵。在Reduce阶段，为了处理在高密集和高曲率的数据区域可能产生的过拟合线段，将Map输出的所有线段合并成线段矩阵后，使用算法2过滤过拟合线段。

算法2FilterOverfitLines

输入：线段端点矩阵L，列为线段端点坐标，如(2i,2i+1)列组成线段si，过拟合线段的距离λσ2，λ为自定义参数，σ2为噪声方差。

输出：消除过拟合线段后的L矩阵。

(1) 排序，将L按线段长度降序排列。

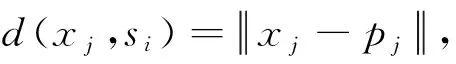
(4)

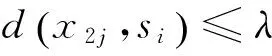
(3) 调整线段，求

(5)

(4) 消除线段，从L矩阵中删除在Cl,Cr中的线段索引列，重复步骤(2)。

ReduceTask中，连接局部主成分线段类似于求解数学领域中著名的旅行商问题(Travellingsalesmanproblem,TSP)，将其转化成找一条哈密顿路径使得总代价最小，输出为〈L,IndexArr〉,L为线段矩阵，IndexArr为顺序连接L的列索引。假设有k条线段s1,s2,…,sk，使用贪婪算法求解该问题，算法如下：

算法3LinkLines

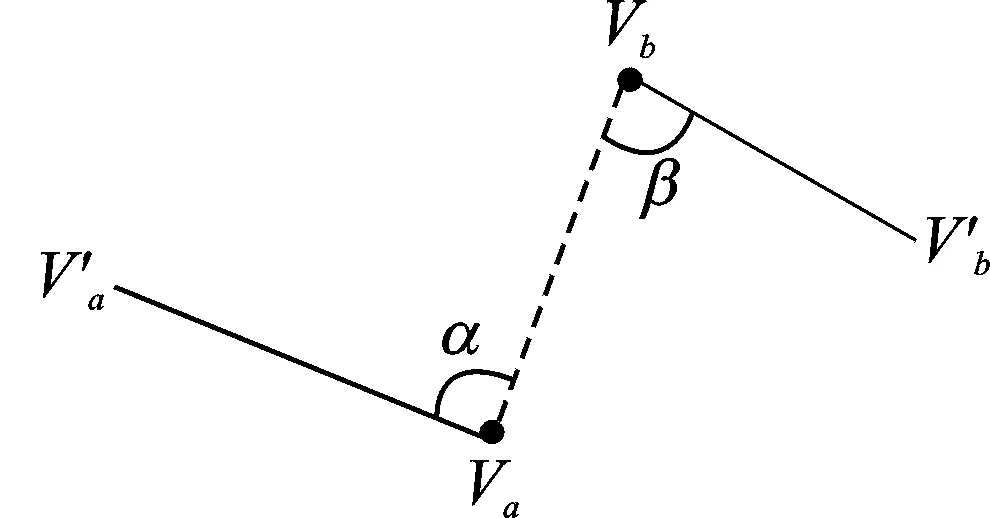
图2 连接两个哈密顿子图Fig.2 Connecting two Sub-PLs

输入：线段矩阵L，L列为线段端点坐标

输出：顺序连接L的列索引

(1) 令h=k，初始有h个哈密顿子图。

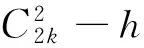
(3) 重复步骤(2)，最终产生最佳线段e1,e2,…,ek-1的端点连接顺序索引。为了更加直观地展示整个思路过程，DisSKPC整体流程示意图如图3。

3 实验及分析

集群环境基于Spark1.4.0MapReduce计算框架，使用Hadoop2.6Yarn作为资源管理器，采用Scala语言编写。使用J.J.Verbeek[7-8]在测试SKPC算法时产生数据的脚本生成本实验的数据集，节点属性信息如表1所示。

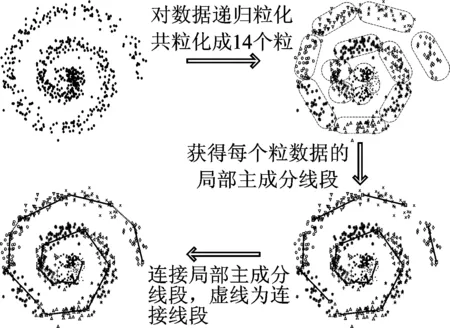
图3 分布式软K段主曲线流程示意图Fig.3 Diagram of DisSKPC

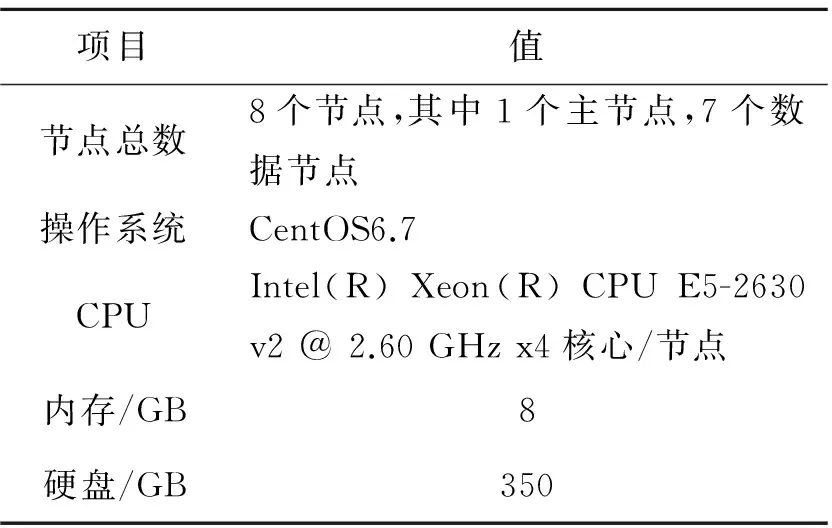
项目值节点总数8个节点,其中1个主节点,7个数据节点操作系统CentOS6.7CPUIntel(R)Xeon(R)CPUE5-2630v2@2.60GHzx4核心/节点内存/GB8硬盘/GB350

3.1 有效性分析

本实验的目的是测试DisSKPC算法的可行性，图4对比了SKPC算法和DisSKPC算法的效果。图4(a,c,e)是SKPC的运行结果，图4(b,d,f)是DisSKPC运行结果，其中不同的颜色代表不同的粒数据，N为数据总量，σ为噪声方差，T为每粒数据量阈值。从图4(a)可以看出，即使针对全局进行优化，在数据高密集和高曲率区域，SKPC算法仍有过拟合存在，而图4(b)，高密集的数据区域被粒化成多个粒，有效地避免了过拟合产生。图4(c)和图4(d)图相比，在顶点处，DisSKPC拟合效果更佳，但某些区域局部噪声较大，产生的线段方向和数据整体分布有偏差。图4(e)和图4(f)相比，两种算法都存在欠拟合现象，但从整体来看，DisSKPC在局部区域拟合效果更好，所以DisSKPC效果更佳。综上所述，DisSKPC拟合效果和串行SKPC算法有较高的一致性，都能比较完好地拟合出数据的分布。从原理上分析，SKPC算法插入一条新线段是通过比较数据集中所有的点，计算各点周围的数据点到最邻近的线段距离总和及到该点的距离总和，如果二者差值最大，将该点及其周围的点组成的区域作为数据块提取第一主成分线段，而这样的区域往往密集度较高，与先对数据粒化，将这些密集度较高的区域预先提取出来，再计算这些区域的第一主成分线段有着异曲同工之妙。

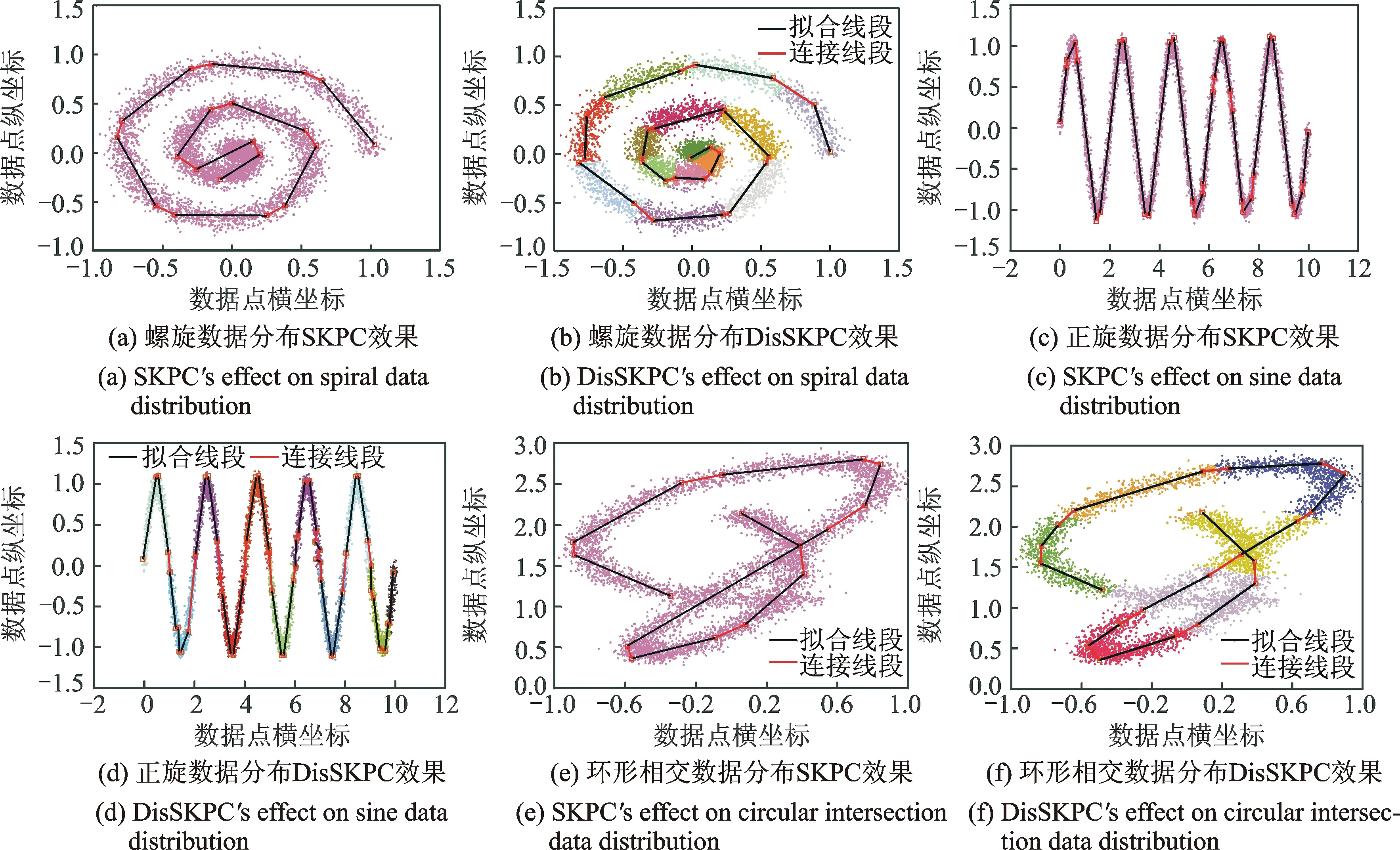
图4 SKPC与DisSKPC效果对比图Fig.4 Effect comparison of SKPC and DisSKPC

3.2 对比性分析

本实验的目的是为了比较串行SKPC算法和DisSKPC算法的效率。数据来源于将图4(c)的数据横向叠加，节点数目均为5，粒化阈值T=2 000，这里运行时间均为平均时间。从表2可以看出，当数据集较小时，串行SKPC算法有着更高的效率，这是因为DisSKPC算法集群节点的通讯和数据粒化都需要时间。当数据量N=4 000时，DisSKPC的并行使运行时间更短，并且串行算法由于内存的限制，难以处理数据量大于10 000的数据集。综上所述，并行DisSKPC算法更适合大规模数据集，具有更高的效率。

表2 SKPC和DisSKPC运行时间对比

Tab.2 Running time comparison of SKPC and DisSKPC

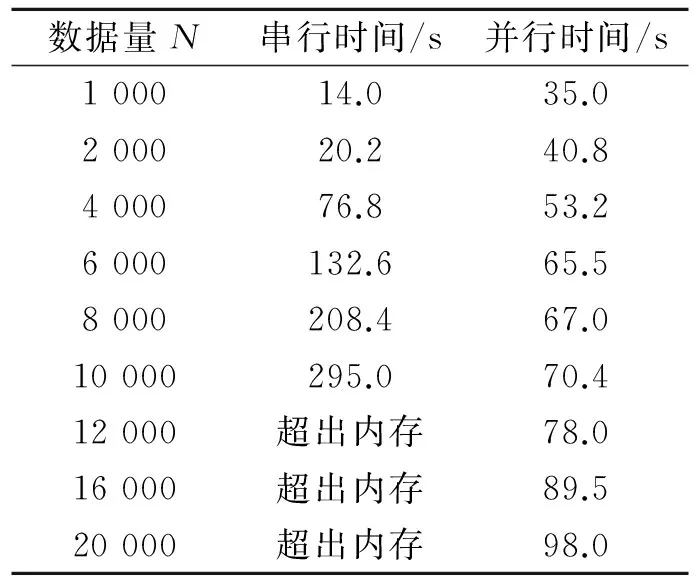
数据量N串行时间/s并行时间/s100014.035.0200020.240.8400076.853.26000132.665.58000208.467.010000295.070.412000超出内存78.016000超出内存89.520000超出内存98.0

3.3 性能分析

本节分别分析了计算节点的数目和粒化阈值T对算法性能的影响，数据来源于将图4(c)的数据横向叠加，实验结果为多次计算取平均值。

3.3.1 不同节点数对运行时间的影响

本实验的目的在于测试DisSKPC算法的并行性能，即运行时间随节点数目增加的变化情况。实验中，对于同一个数据集N=20 000，阈值T=2 000。从图5的实验结果可以看出，当节点数小于5时，随着节点数目的增加，DisSKPC的运行时间都呈下降趋势，这说明MapReduce 框架本身保证了DisSKPC算法的伸缩性，但需要注意的是随着节点数目的增多，节点之间通讯的时间消耗也必然增加，因此运行时间下降比率并不呈现线性；当节点数量继续增加时，算法的运行时间反而增加，这是因为这时增加一个节点带来的通信和调度等固有时耗大于任务并行化所带来的时间节省。所以总体上会出现前期运行时间随着节点的增多而减少，而后期随着节点数量的增多而增加的现象。

3.3.2 参数T对运行时间的影响

SKPC算法计算单个粒的时间对DisSKPC的运行时间有很大影响，所以对T的取值进行了实验，希望得出一个比较好的T值范围。实验中，使用数据集N=20 000，节点数目均为5。从图6的实验结果可以看出，T≤3 500时算法的运行时间增长率比较小，这是因为SKPC算法计算单个粒数据的局部主成分线段的时间相差并不大，但算法需要并行的任务数减少了。当T>3 500时，算法的运行时间急剧增大，这是因为这个时候SKPC算法计算单个粒数据局部主成分线的时间，远大于将粒粒化成更小的粒，再提取局部主成分线段的时间总和。需要指出，T在4 000～4 500和5 000～6 000时运行时间相差并不大，这是因为初始粒化的粒个数一样，导致最后粒的大小相差不大。综上所述，每粒数据量的阈值T≤3 500能节省大量的运行时间。

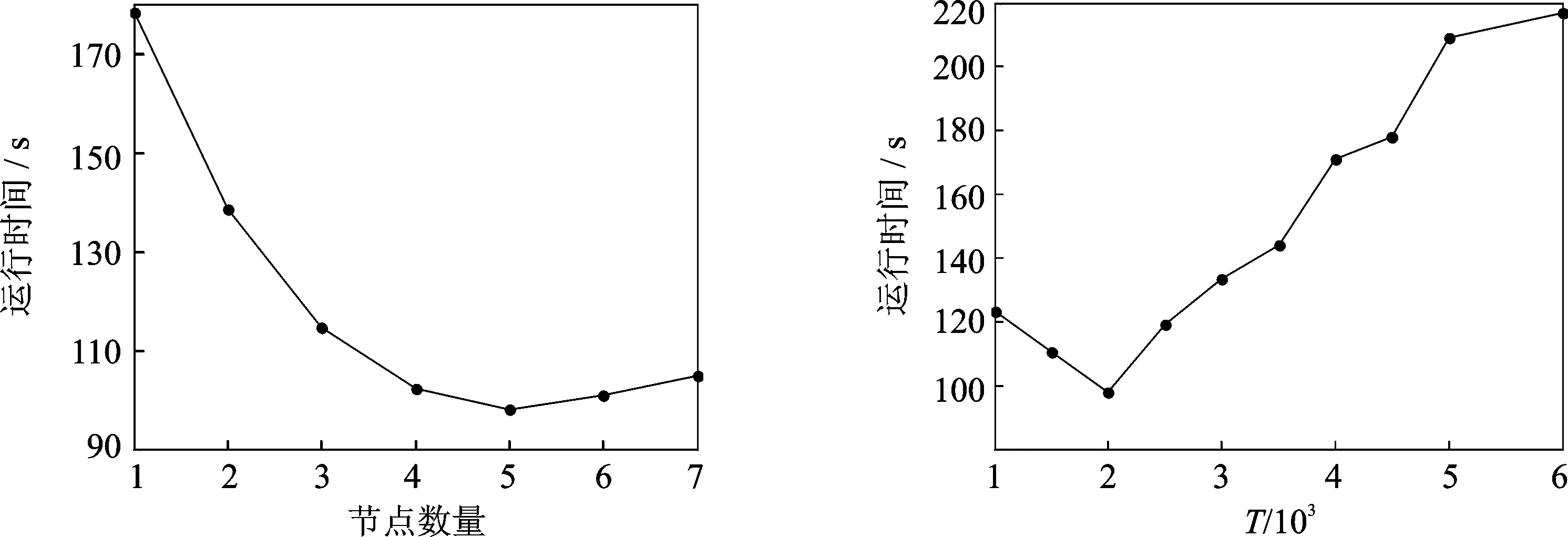
图5 不同节点数量对应的算法性能 图6 T对性能的影响Fig.5 Performance of different numbers of nodes Fig.6 Effect of T on performance

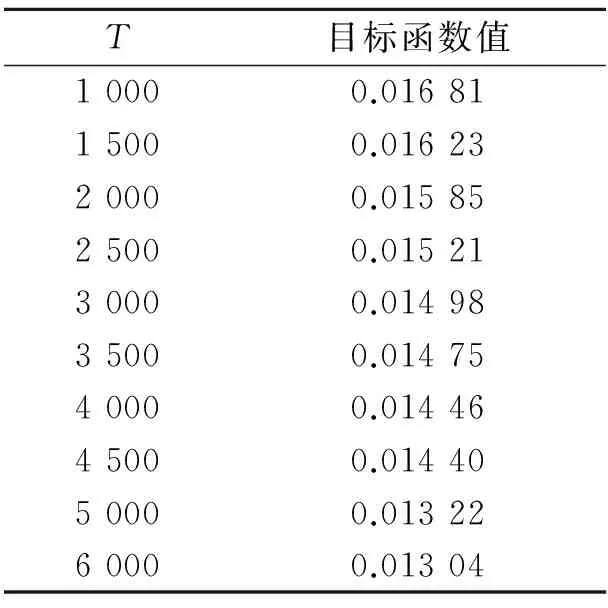
Tab.3 Value of objective function

3.3.3 参数T对数据拟合效果的影响

对给定数据点采用SKPC的目标函数来评估所得主曲线对数据的拟合效果，函数值越小，算法对数据的拟合效果越好

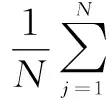
(6)

式中：α=2(d-1)σ2，σ为初始的噪声方差，d为数据的维度，l为拟合线段总长度。在ReduceTask中计算目标函数的值，以评估T对DisSKPC算法效果的影响。从表3的结果知道，随着T的增大，F逐渐减小，这是因为T越大，单个任务针对的拟合数据区域越大，越能接近全局的效果。但总体上，T的取值对目标函数影响并不大，其都能较好地拟合数据分布。

4 结束语

本文深入分析了传统主曲线的优缺点，发现其难以处理海量数据，针对该问题，设计并实现了基于MapReduce的分布式SKPC算法。通过多个角度进行了实验，结果表明提出算法的可行性和良好的伸缩性，并且通过调整T，还能较好地避免SKPC算法产生的过拟合现象。但本算法也有不完善的地方，如T需预先设定，不能自适应地选取一个最好的T使得算法的性能最好，在下一步工作中将进行探索和改进。主曲线在维数约简、数据可视化和模式识别等诸多领域有着广泛使用，本文提出的方法不仅为海量数据主曲线学习提供一种新的解决方案，而且对推动非线性智能信息处理的发展具有重要的理论意义。

[1] Baldi P, Hornik K. Neural networks and principal component analysis:Learning from examples without local minima[J].Neural Networks, 1989, 2(1):53-58.

[2] Hastie T, Stuetzle W. Principal curves[J].Journal of the American Statistical Association, 1989, 84(406):502-516.

[3] Banfield J D, Raftery A E. Ice floe identification in satellite images using mathematical morphology and clustering about principal curves[J].Journal of the American Statistical Association, 1992, 87(417):7-16.

[4] Tibshirani R. Principal curves revisited[J].Statistics & Computing, 1999, 2(4):183-190.

[5] Kégl B, Krzyzak A, Linder T, et al. Learning and design of principal curves[J].Pattern Analysis & Machine Intelligence IEEE Transactions on, 2000, 22(3):281-297.

[6] Delicado P. Another look at principal curves and surfaces[J].Journal of Multivariate Analysis, 2001, 77(1):84-116.

[7] Verbeek J J, Vlassis N, Krose B. A k-segments algorithm for finding principal curves[J].Pattern Recognition Letters, 2002, 23(2):1009-1017.

[8] Verbeek J J, Vlassis N, Kröse B. A soft k-segments algorithm for principal curves[M].Berlin, Heidelberg:Springer,2001:450-456.

[9] Liu X, Jia Y. A bottom-up algorithm for finding principal curves with applications to image skeletonization [J].Pattern Recognition,2005,38(7):1079-1085.

[10]张红云. 基于主曲线的脱机手写字符识别的研究[D]. 上海:同济大学, 2005.

Zhang Hongyun. Research on off-line handwritten digit recognition based on principal curves[D].Shanghai:Tongji University, 2005.

[11]Einbeck J, Tutz G, Evers L. Local principal curves[J].Statistics & Computing, 2005,15(4):301-313.

[12]Zhang J, Chen D. Constraint k-segment principal curves[J].Lecture Notes in Computer Science, 2006, 4113(2):345-350.

[13]Zhang J, Wang X, Kruger U, et al. Principal curve algorithms for partitioning high-dimensional data spaces[J].Neural Networks IEEE Transactions on, 2011,22(3):367-380.

[14]Ozertem U, Erdogmus D. Locally defined principal curves and surfaces[J].Journal of Machine Learning Research, 2011,12(4):1249-1286.

[15]Zhang H, Pedrycz W, Miao D, et al. A global structure-based algorithm for detecting the principal graph from complex data[J].Pattern Recognition, 2013, 46(6):1638-1647.

[16]Zhang H, Pedrycz W, Miao D, et al. From principal curves to granular principal curves[J].IEEE Transactions on Cybernetics, 2014, 44(6):748-760.

[17]Aliyari Ghassabeh Y, Rudzicz F. Incremental algorithm for finding principal curves[J].Iet Signal Processing, 2015, 9(7):521-528.

[18]Vernica R, Carey M J, Li C. Efficient parallel set-similarity joins using MapReduce[C] // ACM SIGMOD International Conference on Management of Data, SIGMOD 2010. Indiana: [s.n.] , 2010:495-506.

[19]Dean J, Ghemawat S. MapReduce:Simplified data processing on large clusters[J].Proceedings of Operating Systems Design and Implementation, 2004, 51(1):107-113.

[20]鲁伟明, 杜晨阳,魏宝刚,等. 基于MapReduce的分布式近邻传播聚类算法[J].计算机研究与发展, 2012,49(8):1762-1772.

Lu Weiming, Du Chenyang, Wei Baogang, et al. Distributed affinity propagation clustering based on MapReduce[J].Journal of Computer Research and Development, 2012, 49(8):1762-1772.

[21]王诏远, 李天瑞, 易修文. 基于MapReduce的蚁群优化算法实现方法[J].计算机科学, 2014, 41(7):261-265.

Wang Zhaoyuan, Li Tianrui, Yi Xiuwen. Approach for development of ant colony optimization based on MapReduce[J].Computer Science,2014,41(7):261-265.

[22]郭进伟, 皮建勇. 基于MapReduce的SON算法实现[J].计算机应用, 2014(S1):100-102.

Guo Jinwei, Pi Jianyong. Implementation of SON algorithm based on MapReduce[J].Journal of Computer Applications, 2014(S1):100-102.

[23]刘祥哲, 刘培玉, 任敏,等. 基于负载均衡和冗余剪枝的并行FP-Growth算法[J].数据采集与处理, 2016,31(1):223-230.

Liu Xiangzhe, Liu Peiyu, Ren Min, et al. Parallel FP-Growth algorithm based on load balancing and redundancy pruning[J].Journal of Data Acquisition and Processing, 2016,31(1):223-230.

[24]戴健, 丁治明. 基于MapReduce快速kNN join方法[J].计算机学报, 2015, 38(1):99-108.

Dai Jian, Ding Zhiming. MapReduce based fast kNN Join[J].Chinese Journal of Computers, 2015, 38(1):99-108.

[25]Li Q, Wang P, Wang W, et al. An efficient k-means clustering algorithm on MapReduce[M].Switzerland:Springer International Publishing, 2014:357-371.

[26]Cui X, Zhu P, Yang X, et al. Optimized big data k-means clustering using MapReduce[J].Journal of Supercomputing, 2014, 70(3):1249-1259.

[27]焦娜. 改进的软K段主曲线算法及其在指纹骨架提取中的应用[J]. 数据采集与处理, 2015, 30(5):1070-1077.

Jiao Na. Improved soft K-Segments algorithm for principal curves and its applications on fingerprint skeletonization extraction[J].Journal of Data Acquisition and Processing, 2015, 30(5):1070-1077.

[28]Yang M, Liao Z W. The skeletonization research of low-quality Chinese characters based on principal curves[C]// Machine Learning and Cybernetics, 2009 International Conference. Baoding, China: Institute of Electrical and Electronics Engineers, 2009:3238-3241.

[29]张红云, 苗夺谦, 傅文杰. 基于改进的GPL主曲线算法的指纹特征分析与提取[J].模式识别与人工智能, 2007, 20(6):763-769.

Zhang Hongyun, Miao Duoqian, Fu Wenjie. Analysis and extraction of fingerprint minutiae based on improved GPL principal curve algorithm[J].Pattern Recognition and Artificial Intelligence, 2007, 20(6):763-769.

[30]Srinath N K. MapReduce design of K-Means clustering algorithm[C]// Information Science and Applications, 2013 International Conference. Suwon: Institute of Electrical and Electronics Engineers, 2013:1-5.

The traditional principal curves algorithm can obtain good results on small datasets. But the computing and storage resources of a single node cannot meet the requirements of the extraction of principal curves on massive datasets.Distributed parallel computing is one of the most effective way to solve the problems. Therefore, we proposed a distributed soft K-segments algorithm for principal curves based on MapReduce, named DisSKPC. First, we recursively granulated all the numerical data into information granules to limit each granular size and ensure the relevance of the data in the granules using the distributed K-Means algorithm. Then we calculated the local principal component segments of each granule and eliminated over-fitting segments that may arise in the area of high-density and high-curvature using the noise variance. Finally, we connected these local principal component segments using the Hamiltonian path and greedy algorithm, forming a best curve through the middle of the data cloud. Experimental results demonstrate the feasibility and scalability of the proposed DisSKPC algorithm.

distributed parallel; principal curves; data granulation;MapReduce

国家自然科学基金(61573255)资助项目；上海市进一步加快中医药事业发展三年行动计划重点(ZY3CCCX36002)资助项目；中央高校基本科研业务费(0800219302)资助项目；上海市自然科学基金(14ZR1442600)资助项目。

2016-03-31；

2016-06-07

TP391

A

胡作梁(1990-)，男，硕士研究生，研究方向：认知与智能信息处理，E-mail：huzuoliang1990@163.com。

张红云(1972-)，女，博士，副教授，研究方向：主曲线、粒计算和粗糙集等。

Distributed Soft K-Segments Algorithm for Principal Curves Based on MapReduce

Hu Zuoliang1,2， Zhang Hongyun1,2

(1.Department of Computer Science and Technology, Tongji University, Shanghai, 201804, China; 2.Key Laboratory of Embedded Systems and Service Computing of Ministry of Education,Tongji University, Shanghai, 201804, China)