关于一类特殊函数方程的解及性质
赵 教 练
(渭南师范学院 数理学院,陕西 渭南 714099)
【自然科学基础理论研究】
关于一类特殊函数方程的解及性质
赵 教 练
(渭南师范学院 数理学院,陕西 渭南 714099)
引入q-Gamma函数,并通过求解一类特殊的q-Gamma函数方程,利用解析法给出了有关q-Gamma函数比率的性质及其推论。在其推广之下,将结果应用于研究有关Gamma和q-Gamma函数的比率不等式,得到了一类特殊函数方程的解及其性质。
Gamma函数;q-Gamma函数;比率;不等式
1 基本概念
Gamma函数是数学物理和特殊函数论中的重要函数,在函数论、概率论、数论和组合数学中都有重要的应用。Gamma 函数及其推广的 Gamma 函数的单调性可用于证明一些著名的不等式,Gamma函数的无穷级数展开可用于计算数论中一些算术函数在特殊点的值。
经典的Euler Gamma函数定义为:

1869年,J.Thoma[1]推广了Gamma函数,定义了Γq函数:对任意的正实数x和q(q≠1),有
(1)
(2)
1904年,F.H.Jackson[2]也讨论了Γq函数的推广形式和解析性质。基于Gamma函数在分析、数论、概率论、逼近论、数学物理等领域的重要应用[3-4],最近几年,很多学者研究了Gamma函数及其推广的Γq函数的性质[5-7],并且证明了推广的Γq函数与欧拉Γ函数
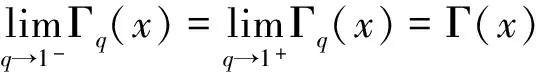
利用J.Thoma给定的(1)式和(2)式,可以得到类似的函数方程式
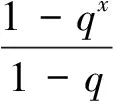
(3)
由此可以推导类似Gamma函数的递推公式。如果q→1,则
Γ(x+1)=xΓ(x),x>0。
(4)
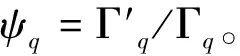
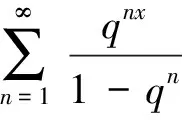
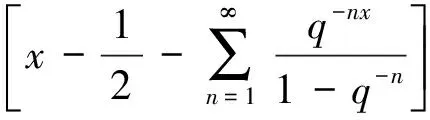
上述公式可以从J.Thoma定义的(1)式和(2)式推算得到。[9-11]
2 主要结果
1948年,W.Krull研究一般函数方程f(x+1)=φ(x)f(x),证明了如果φ满足一定条件,则具有对数性质的凹函数的解f具有存在性和唯一性。更精确地说,建立了以下结果。
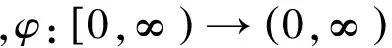
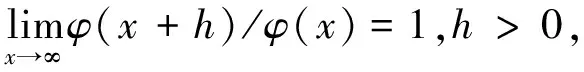
(5)
则
f(x+1)=φ(x)f(x),x≥0且f(0)=α
(6)
存在唯一的正解。[11]对于解f,在[0,∞)上是对数凹的,并且满足对于充分小的h>0,有
Krull提供了(6)式解的级数表达式。
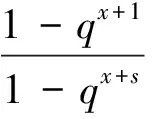
通过计算表明φq,s在[0,∞)上是对数凸的,且满足(5)式,所以Krull的命题揭示了(6)式存在一个对数凹解。
定理1 令α>0,s∈(0,1)是一个实数。函数方程
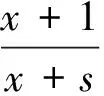
(7)
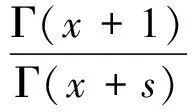
证明 利用公式(4),可以得出f(x)=αΓ(s)Γ(x+1)/Γ(x+s)满足(7)式。
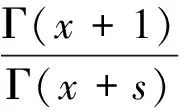
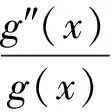
其中:ψ=Γ′/Γ为Γ函数的对数导数。利用积分表示


以及Laplace变换的卷积定理,可以得到
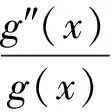
(8)
其中:

(9)
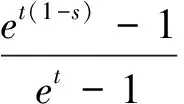
计算表明,在(0,∞)上Δ′/Δ是严格递减的。令t>0,那么有
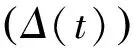
(10)
其中:p(x)=x2-s-(1-s)2x2+2s(s-2)x+xs-(1-s)2,x=et>1。
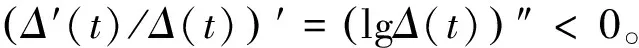
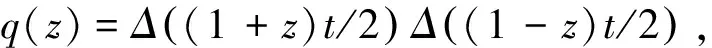
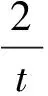
因为0<(1-z)t/2≤(1+z)t/2,所以Δ′/Δ的单调性揭示了
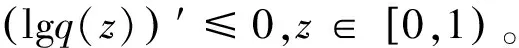

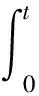
所以,对t>0,由公式(9)可以得出


(11)
利用(8)式和(11)式可以推得,对x≥0,g″(x)<0,由于满足(7)式的凹函数在[0,∞)上必须是正的,则得出严格凹函数f(x)=αΓ(s)Γ(x+1)/Γ(x+s)是(7)式唯一确定的解。
定理2 令α>0,q∈(0,1),s∈(0,1)是一个实数,函数方程
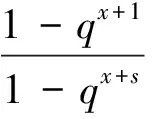
(12)
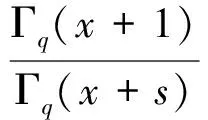
证明 应用函数方程式(3)得出f(x)=αΓq(s)Γq(x+1)/Γq(x+s)是(12)式的一个解。因为凹解必须是正的,所以从命题得出结论,f(x)是唯一确定的。
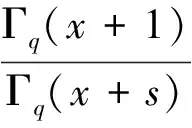
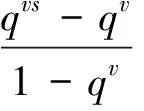
为了证明对x>0有g″(x)<0,只需证明
avan-v (13) q1h(q2) (14) 其中:0 如果h(x)是递减的,那么(14)式就成立。 (15) 且z=yk∈(0,1)。 由于vzv+1-n+(n-v)z1-v≥v+(n-v)=n,z∈(0,1),由此,结合(15)式可以得到:当y∈(0,1)时,有h′(y)<0。 [1] Rubel L A.A survey of transcendentally transcendental functions[J].American Mathematical Monthly,1989,96(9):777-788. [2] Davis P J.Leonhard Euler’s Integral:A Historical Profile of the Gamma Function:In Memoriam:Milton Abramowitz[J].American Mathematical Monthly,1959,66(10):849-869. [3] 窦向凯,尹枥.关于Gamma函数的几个不等式[J].滨州学院学报,2008,24(6):69-71. [4] 华东师范大学数学系.数学分析:下册[M].北京:高等教育出版社,2010:145-150. [5] 赵教练.关于q-Gamma函数及对数导数的性质[J].渭南师范学院学报,2012,27(10):8-10. [6] 张永利.关于伽马分布及相关分布性质的一点研究[J].大学数学,2012,28(3):135-140. [7] 王高雄.常微分方程[M].北京:高等教育出版社,2004:53-55. [8] 杨帆,陈超平.关于Gamma函数和Psi函数的性质[J].河南理工大学学报(自然科学版),2009,28(6):816-819. [9] 李爱军,普丰山.Gamma函数的对数完全单调性[J].信阳师范学院学报(自然科学版),2006,19(4):381-383. [10] Zhao J L,Luo Q M,Guo B N,et al.Logarithmic convexity of Gini means[J].Journal of Mathematical Inequalities,2015,6(4):509-516. [11] Qi F,Guo B N.Sharp inequalities for polygamma functions[J].Mathematica Slovaca,2015,65(1):103-120. 【责任编辑牛怀岗】 SolutionandPropertiesofq-GammaFunctionEquations ZHAO Jiao-lian This paper solved a kind of function equation of q-Gamma. The paper mainly shows the important theorems of the solution of q-Gamma functions, proving these theorems and studies the inequality of the ratio of q-Gamma functions by applying the results to the inequality. Gamma function; q-Gamma function; ratio; inequality O174.66 :A :1009-5128(2017)16-0010-04 2016-11-17 中国博士后基金项目:云计算中外包数据安全的关键密码技术(2015M582619);陕西省教育厅自然科学专项计划项目:椭圆函数论及其在数论和组合中的应用研究(15JK1264);渭南师范学院自然科学类人才项目:特殊函数及其在完全单调理论和数论中的应用研究(15ZRRC05);渭南师范学院教育教学改革研究项目:分类探究模式在《数学分析》课程改革中的创新与实践(JG201549) 赵教练(1978—),男,陕西兴平人,渭南师范学院数理学院副教授,理学博士,主要从事函数论、密码与信息安全研究。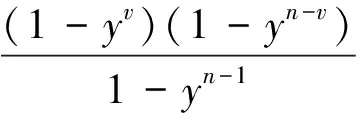


(School of Mathematics and Physics, Weinan Normal University, Weinan 714099, China)

