考虑现浇砼收缩与滑移时叠合板承载力的研究

黄玉梁, 盛宏玉, 王宗磊(合肥工业大学 土木与水利工程学院,安徽 合肥 230009)

考虑现浇砼收缩与滑移时叠合板承载力的研究

黄玉梁, 盛宏玉, 王宗磊
(合肥工业大学 土木与水利工程学院,安徽 合肥 230009)

基于ANSYS有限元软件,文章应用弹簧单元和生死单元对混凝土叠合板进行建模,分别考虑叠合面滑移、二次受力、现浇层混凝土收缩等因素的影响,研究叠合板的极限承载力并与整浇板进行对比。计算结果表明:叠合面的滑移对承载力的影响较小;施工过程中的二次受力可有效提高叠合板的承载能力;同时,现浇层混凝土的收缩会明显削弱叠合板的整体承载能力,且承载力随着收缩微应变的增大而迅速减小。

混凝土;二次受力;叠合面滑移;混凝土收缩;承载力;ANSYS软件

0 引 言

叠合板根据其使用和制造时的受力特点可分为预制部分和现浇部分。预制部分在工厂制造,然后构件承受施工阶段的荷载,同时作为现浇混凝土层的模板。这种构件与装配式结构相比,具有整体性能好、抗震性能优越的优点;与传统现浇结构相比,则具有省材、施工简便、工期短等优点。

由于叠合板组成材料的复杂性,再加上结构的特殊性,造成了相同截面上现浇和预制部分的混凝土应力应变的非线性变化,存在受拉钢筋“应力超前”和现浇混凝土“受压应变滞后”的现象,其受力性能和整浇板相比有较大的差异,同时现浇混凝土的收缩对叠合板承载力也有较大的影响。对于预制混凝土叠合板承载力的研究,已有很多的研究成果。

文献[1]通过理论分析与试验,研究了预应力混凝土薄板与叠合板开裂弯矩相关性模式;文献[2]研究了预应力混凝土空心叠合板的抗裂性及裂缝发展规律、挠度、承载力等结构性能,分析了跨高比、配筋率等影响预应力混凝土空心叠合板破坏性能的主要因素;文献[3-4]通过普通钢筋混凝土剪力墙和预制叠合板式混凝土剪力墙的荷载试验,对剪力墙的承载力、变形特征及耗能进行比较,重点探讨了叠合面的抗剪强度;文献[5]对钢筋混凝土叠合结构的二次受力过程进行了数值模拟,并分析了新旧混凝土叠合面之间的粘结滑移关系;文献[6]对PK 预应力混凝土叠合板的抗弯性能进行了模拟和试验研究,对比分析了叠合板的开裂荷载和极限承载力。

由于叠合板二次浇筑、两阶段受力的特点,迄今为止,对其受力机理和破坏形态仍没有一个统一和清晰的认识。虽然国内外众多学者通过对叠合板的试验和理论研究得出了一些有价值的结论,但很少考虑现浇混凝土收缩微应变的影响。本文采用ANSYS软件对混凝土叠合板进行了非线性有限元三维建模及全过程分析,通过计算分析和结果比较进一步了解新旧混凝土叠合面滑移、二次受力及现浇混凝土收缩对叠合板承载能力的影响。

1 有限元建模

1.1 混凝土本构关系

混凝土单轴受压的本构关系采用Saenz公式来描述[7]，其应力-应变关系曲线如图1所示。

混凝土应力-应变关系式如下：

(1)

其中,E0为原点切线模量;Ec为峰值点的割线模量;σ0、ε0分别为应力峰值和相应的应变,取ε0=0.002;εcu为混凝土极限压应变,取εcu=0.003 3。

1.2 钢筋本构关系

钢筋采用双线性随动强化模型,对应于Von-Mises屈服准则[8],其应力-应变关系曲线如图2所示。

具体关系式如下：

(2)

其中，fy为钢筋的屈服强度;Es=200 GPa,为弹性模量;εy为钢筋的屈服应变,εy=fy/Es。

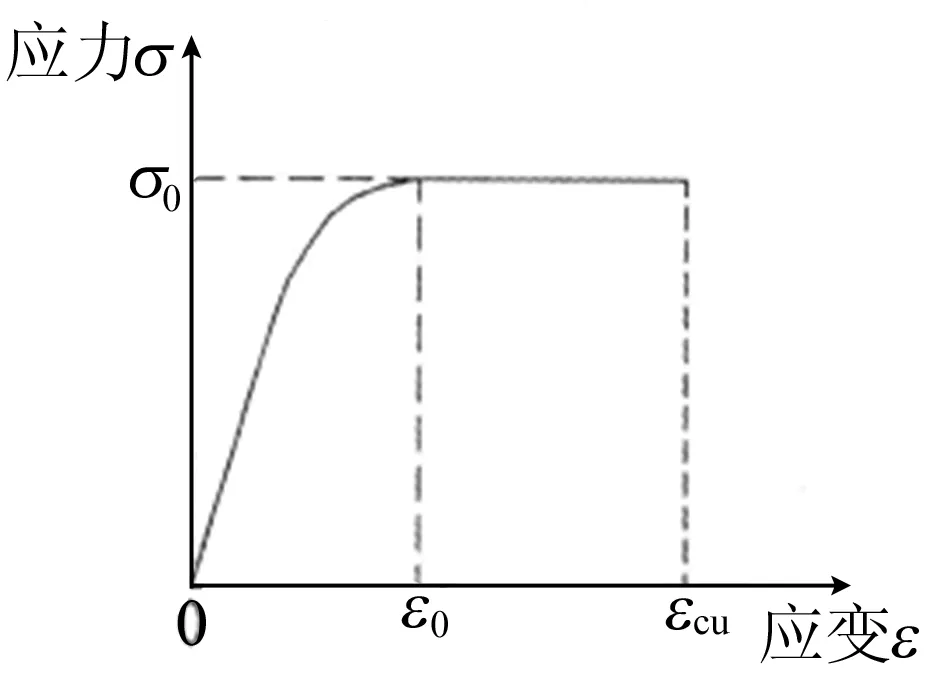
图1 混凝土应力-应变关系曲线

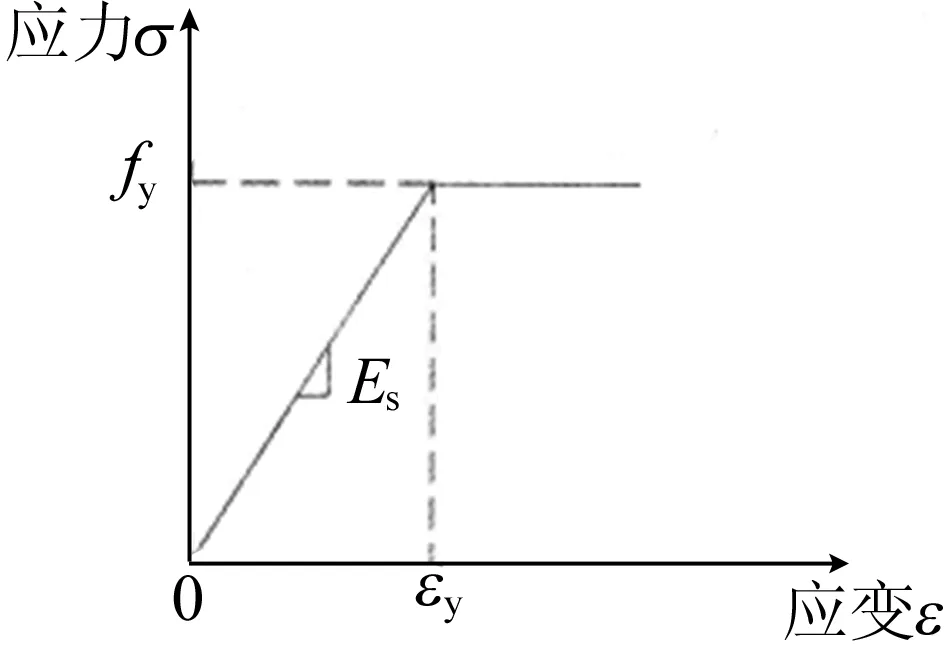
图2 钢筋应力-应变关系曲线

1.3 弹簧单元

在本文的有限元分析中,采用COMBIN39单元来模拟叠合层上下混凝土的联结,即在混凝土单元结点之间插入有位置无体积的弹簧单元,使上下两层混凝土单元在外荷载作用下通过弹簧单元发生相对滑移。根据文献[8]所建模型的基本方程如下:

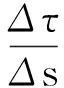
(3)

其中,k为粘结滑移曲线的斜率；Δτ为局部坐标下粘结应力增量；Δs为局部坐标下粘结滑移增量；A为从属于一个弹簧的混凝土单元的表面积。

本文假定混凝土竖向联结为刚性的,也不考虑叠合板的侧向滑移,只考虑纵向的水平滑移。(3)式中的刚度系数k与叠合面的凿毛程度和杂物清理状况有关,一般需通过实验来确定。文献[8] 在2块预制砼中间的后浇混凝土块上用千斤顶施加集中荷载,通过5组试验的结果,得到Δτ/Δs的平均值约为19.0 MPa/mm,本文在计算时参考此数值。

1.4 现浇混凝土收缩微应变的模拟

本文采用降温法来模拟现浇混凝土的收缩。取混凝土的热膨胀系数αC=1×10-5/℃,混凝土的收缩在早期发展较快,以后逐渐缓慢,最终趋于稳定,其收缩微应变受浇筑季节和时段的影响较大,不是一个定值,通常情况下,收缩值ε在2×10-4～5×10-4之间,相当于降温值t在20～50 ℃之间。

1.5 单元类型的选择及单元特性

钢筋单元选用LINK8单元,该单元有2个节点,每个节点有3个平动自由度,即UX、UY、UZ,它可以承受单向拉伸和压缩。混凝土采用SOLID65单元,该单元在普通8节点三维等参元的基础上增加了针对混凝土的材料参数和整体式钢筋模型,能反映混凝土的压碎和开裂。裂缝模拟采用弥散裂缝模型,一旦混凝土的主应力超过了混凝土的抗拉或抗压强度,ANSYS程序就会用不同颜色的线标记开裂或压碎单元的位置，能够很好地模拟混凝土和岩石材料的破坏过程。

1.6 混凝土的破坏准则

混凝土破坏准则采用Willam-Warnk五参数强度准则,用平均剪应力和平均正应力表示的拉、压子午线方程为:

(4)

由于拉、压子午线交于静水压力坐标轴上,(4)式中只有5个参数是独立的,这5个参数可由ANSYS中混凝土材料的输入参数单轴抗压强度fc、双轴抗压强度fcb、单轴抗拉强度ft、围压下双轴抗压强度f1及围压下单轴抗压强度f2确定。

1.7 构件破坏准则

在叠合板的有限元分析中,为了确定其极限承载力,当满足下列任一条件时即认为整体结构破坏：

(1) 板挠度大幅增大而荷载几乎不增加。

(2) 支承点与跨中受压区混凝土单元压碎。

(3) 总体刚度矩阵奇异。

2 叠合板抗弯性能的模拟

2.1 有限元模型

为了研究现浇混凝土层滑移和收缩对叠合板承载力的影响,本文运用ANSYS软件分层建立4种形式的叠合板模型,模型的长、宽、高分别为2 700、600、150 mm,模型的边界条件为在长度方向两对边简支、宽度方向自由,其截面叠合尺寸及界面联结情况见表1所列。

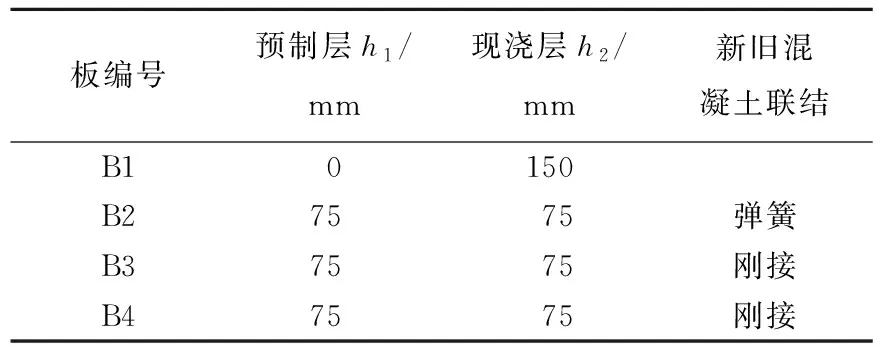
表1 板的尺寸及联结情况

表1中，B1为整浇板；B2和B3可用于分析对比叠合面滑移的影响；B3和B4可用于分析对比现浇混凝土收缩的影响,模型的分析示意图如图3所示(1/2模型)。

图3 有模型的分析示意图

叠合板新旧混凝土强度均为C30,混凝土立方体抗压强度标准值fcu,k=30MPa,单轴抗压强度fc=14.3MPa,单轴抗拉强度ft=1.43MPa,张开裂缝的剪力传递系数βt=0.5,闭合裂缝的剪力传递系数βc=0.95,弹性模量Ec=30GPa,泊松比υc=0.2。钢筋采用HRB400,屈服强度fy=360MPa,弹性模量Es=200GPa,泊松比υc=0.3。钢筋的直径为10mm,间距100mm,不考虑钢筋和混凝土之间的黏结滑移。创建分离式模型时,将几何实体以钢筋位置切分,划分网格时将实体边线定义为钢筋。采用直接将均布荷载(包括自重)施加到有限元模型(节点、单元)上,支座处则采用线约束,为了避免在支座位置处产生应力集中,从而使支座附近节点的混凝土突然破坏造成求解失败,在求解的过程中,宜采用文献[9]提出的方法,在支座处加弹性垫块。考虑到模型的对称性,建立了1/4模型。模型的单元尺寸为50mm,划分网格后的模型如图4所示。

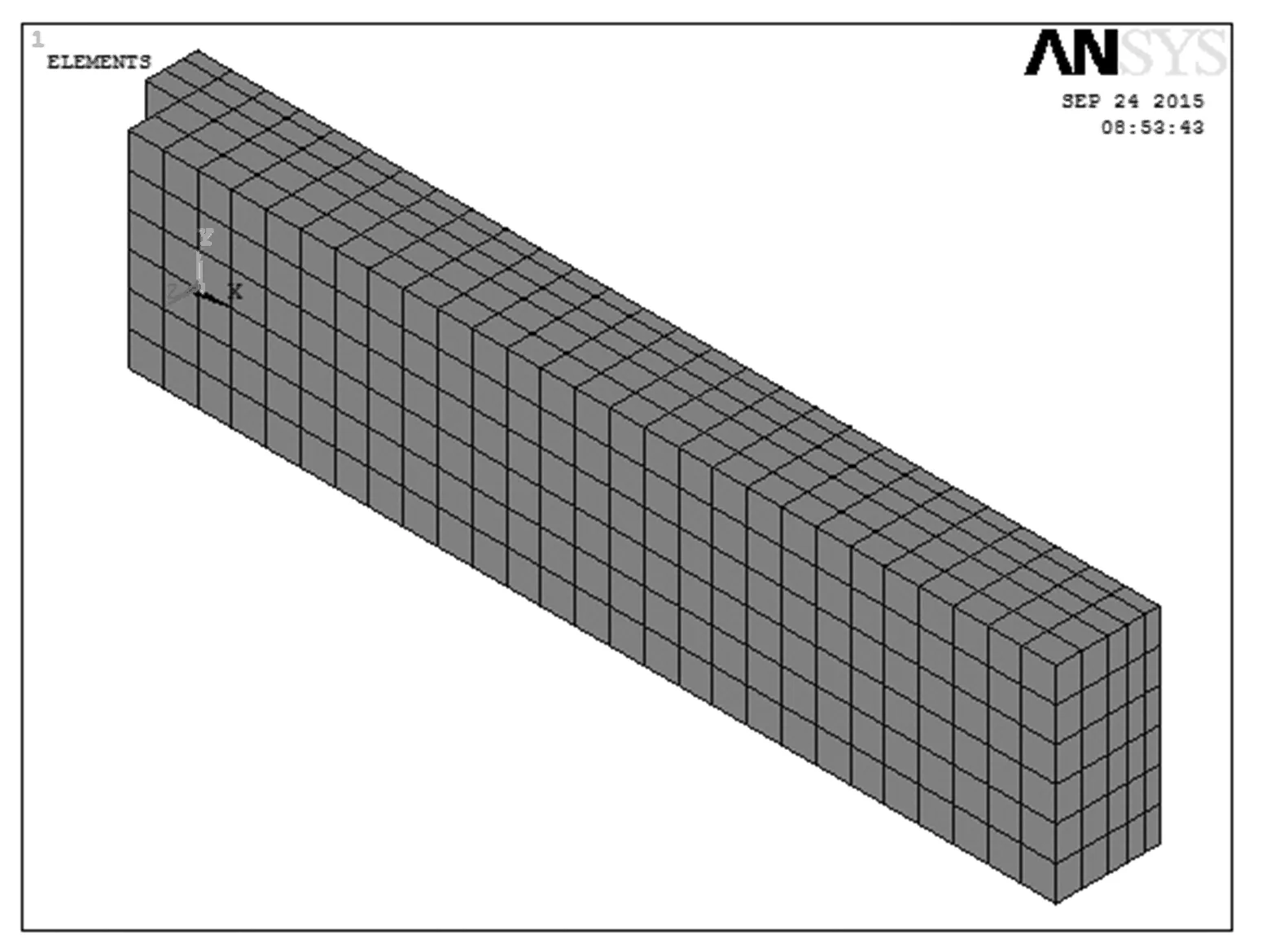
图4 有限元模型网格划分图

对混凝土材料,网格划分不易太密,因为网格划分越密应力集中和软化损伤越明显,也越容易出现不收敛以及错误的结果。

2.2 生死单元的运用

如果模型中加入(或删除)材料,那么模型中相应的单元就存在(或消亡)。单元生死选项就用于在这种情况下杀死或重新激活所选择的单元。叠合板的二阶段制造和二次受力使得其施工过程中载荷的施加涉及初始应力和变形的影响,一阶段荷载作用下预制板将形成初始应力场且产生相应的变形,当现浇混凝土浇注后,在完成养护的过程中存在应力重分布问题。为了有效模拟其受力过程,根据文献[9]介绍的分析步骤及ANSYS中提供的生死单元技术,在初始状态先杀死现浇筑的混凝土单元,对预制部分进行一次受力分析,然后再激活现浇的混凝土单元,对整体结构继续进行二次受力分析。

整浇板B1的分析步骤及荷载设置如下:

(1) 对整浇板施加整体自重。

(2) 对板表面施加均布面荷载,进行抗弯性能分析。

叠合板(B2、B3)的分析步骤及荷载的设置如下:

(1) 杀死现浇混凝土,对预制板施加自重。

(2) 保持现浇混凝土的杀死状态,对预制板上表面施加均布荷载,即相当于现浇混凝土的自重。

(3) 激活现浇混凝土单元,在整体结构的上表面施加均布面荷载,进行抗弯性能分析 (对于设置弹簧单元的叠合板,考虑混凝土单元的面内尺寸为50 mm×50 mm,根据(3)式可取水平弹簧的线刚度k为4.75×105kN/m。

叠合板B4的分析步骤及荷载的设置如下:

(1) 杀死现浇混凝土,对预制板施加自重。

(2) 保持现浇混凝土的杀死状态,对预制板上表面施加均布面荷载和相当于混凝土的自重。

(3) 激活现浇混凝土单元,对现浇混凝土单元施加一定幅度的降温,以模拟现浇混凝土的收缩。

(4) 对整体结构上表面施加均布面荷载,进行抗弯性能分析。

3 计算结果分析

本文基于以上建立的4种叠合板模型进行参数分析,通过对比来考察现浇混凝土的滑移和收缩对叠合板极限承载力的影响。2 700 mm跨度4种类型板的加载直至破坏的全过程曲线如图5所示,其中叠合板的两段不同初始斜率的直线代表两阶段受力的状态,当达到极限承载力时,荷载-位移曲线接近于水平直线段。各板的极限荷载值及破坏时的跨中挠度见表2所列。由计算结果可以看出，ANSYS得到的整浇板纵筋屈服时的荷载为37.40 kN左右,而按现行规范公式[10]计算得到的纵筋屈服点荷载为37.25 kN,两者误差为0.40%,吻合较好。考虑二次受力叠合板破坏荷载大约在39.50 kN,较一般钢筋混凝土整浇板的极限承载力提高了5.61%,这与预期的结果是相符的。计算结果表明，叠合构件能提高板的极限承载能力,ANSYS也能较好地模拟叠合板的受力过程。

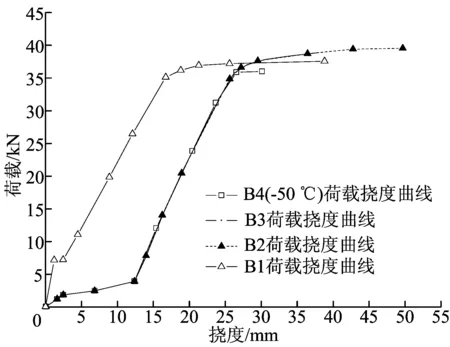
图5 2 700 mm各板的跨中荷载挠度曲线

考虑现浇混凝土收缩效应的叠合板在降温段结束后其挠度有微量的增大,在后续的二次受力过程中,叠合板的受拉钢筋提前屈服,使得整体极限承载力低于普通二次受力叠合板。降温50 ℃二次受力叠合板破坏荷载为36.20 kN,比整浇板的极限承载力降低3.2%,较普通二次受力叠合板的极限承载力降低8.40%;降温25 ℃二次受力叠合板破坏荷载为37.50 kN,和整浇板的承载力相当,较普通二次受力叠合板的极限承载力降低5.10%。

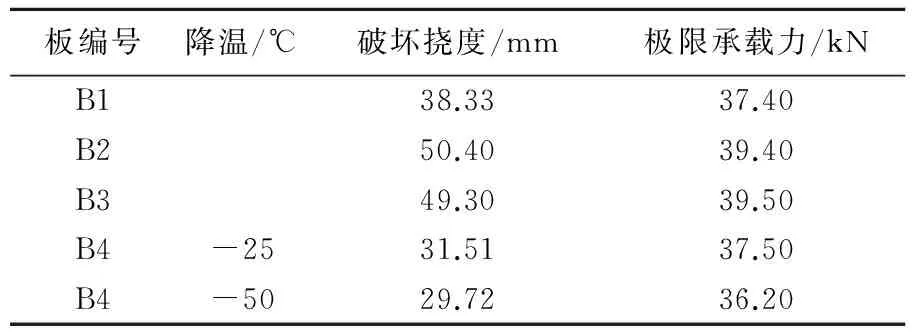
表2 2 700 mm各叠合板的承载力对比

本文用COMBIN14单元模拟叠合面的滑移,由于不涉及动力问题,弹簧不考虑阻尼效应。图4中B2、B3曲线几乎完全重合,说明叠合面的滑移对极限承载力的影响较小。为此本文又在叠合层厚度不变的情况下，考察了板跨度和弹簧刚度变化对叠合板的极限承载力的影响,板的参数及模拟结果见表3所列。由计算结果可以看出:弹簧刚度和跨度的变化对板极限承载力的影响也很小,可以忽略不计;但是随着弹簧刚度的减小,叠合板破坏时的挠度在逐渐增加,因此,其对结构的影响也应该引起重视;在弹簧刚度为4.75×105kN/m时,各跨度的板承载力都略微减小,而弹簧联结大跨度板与相应刚接板的承载力相比相当于破坏提前。本文所给的挠度为破坏前的挠度,并非完全破坏时挠度,因此在大跨度板破坏时挠度略有减小。

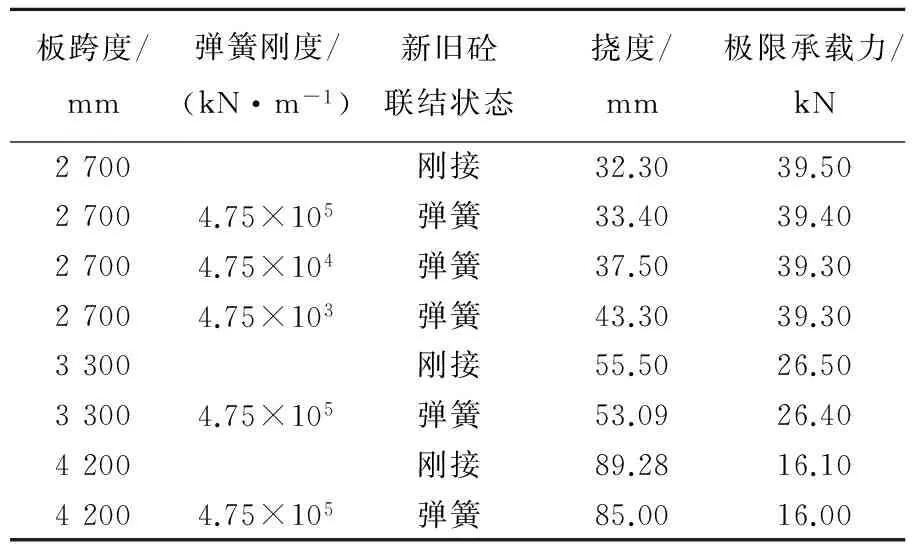
表3 叠合板参数与极限承载力模拟结果

4 结 论

本文分析了整浇钢筋混凝土板、二次受力混凝土叠合板以及考虑混凝土收缩钢筋混凝土叠合板,用ANSYS分别计算了极限承载力,通过有限元分析得出如下结论:

(1) 由整浇板的数值分析可以看出,ANSYS对模拟钢筋混凝土非线性的效果较好,计算出的极限承载力与规范公式给出的结果吻合较好,说明ANSYS可以很好地模拟混凝土板的非线性受力过程,同样也能保证模拟叠合板受力性能的可靠性。

(2) 生死单元的引入使得模拟过程比较真实地再现了叠合结构的二阶段制造和二次受力过程,不同材料之间粘结滑移的考虑使得模拟结果更加接近实际。

(3) 由于二次受力叠合板预制部分预压力的超前,从而有利于叠合板极限承载力的提高。

(4) 叠合面的滑移对承载力的影响较小,但对叠合板的变形有一定影响。通常在预制底板上预留有抗剪受力钢筋,一般情况下可不考虑叠合面滑移的影响,但也要注重叠合面的凿毛和清理工作。

(5) 现浇混凝土的收缩微应变对承载力的影响较大,因此在现浇混凝土的施工时要注意保持适当的温度和湿度,以降低混凝土收缩对叠合板承载力的影响。

[1] 郭乐功,杨艳春,郭乐宁.预应力混凝土叠合板与薄板开裂弯矩相关性分析[J].哈尔滨工业大学学报,2005,37(8):1151-1155.

[2] 刘成才,李九宏.预应力混凝土空心叠合板结构性能试验研究及影响因素分析[J].工业建筑,2011,42(2):35-38.

[3] 刘运林.双向叠合楼板拼缝处受力机理试验研究与数值模拟[D].合肥：合肥工业大学，2003.

[4] 叶献国,张丽军,王德才,等.预制叠合板式混凝土剪力墙水平承载力实验研究[J].合肥工业大学学报(自然科学版),2009,32(8):1215-1218.

[5] 孙冰，丁德馨，曾晟，等.钢筋混凝土叠合结构二次受力过程数值分析[J].华中科技大学学报(城市科学版)，2008，25(4)：260-263.

[6] 黄二位,吕忠珑，马素，等.PK 预应力混凝土叠合板的抗弯性能研究[J].工程建设与设计,2013(7):149-152.

[7] 吕西林，金国芳，吴晓涵.钢筋混凝土结构非线性有限元理论与应用[M].上海:同济大学出版社，1999：33-35.

[8] 鲍戈海.叠合板非线性有限元模拟[D].上海：同济大学,2003.

[9] 祝效华,余志祥.ANSYS高级工程有限元分析范例精选[M].北京:电子工业出版社,2004：38-88.

[10] 中华人民共和国住房和城乡建设部.混凝土结构设计规范:GB 50010-2010[S].北京:中国建筑工业出版社,2010:39-40.

(责任编辑 马国锋)

Researches on bearing capacity of composite slab considering the effect of shrinkage and slippage of cast-in-situ concrete

HUANG Yuliang, SHENG Hongyu, WANG Zonglei
(School of Civil and Hydraulic Engineering， Hefei University of Technology， Hefei 230009， China)

The model of concrete composite slab is established by using the spring element and birth-and-death element based on the ANSYS finite element software. The slippage of laminate surface， secondary loading and shrinkage of cast-in-situ concrete are considered respectively to study the ultimate bearing capacity of composite slab and the results are compared with those of the uniform cast slab. The calculation results indicate that the effect of slippage of laminate surface on the bearing capacity is small. The secondary loading in construction process can increase the bearing capacity effectively. Meanwhile， the shrinkage of cast-in-situ concrete can weaken the bearing capacity obviously. The bearing capacity is lowered rapidly with the increase of micro-shrinkage strain.

concrete; secondary loading; slippage of laminate surface; concrete shrinkage; bearing capacity; ANSYS software

2015-12-03；

2016-02-18

教育部新世纪优秀人才支持计划资助项目 (ncet-12-0838)

黄玉梁(1989-),男,安徽亳州人，合肥工业大学硕士生; 盛宏玉(1957-),男,安徽无为人，合肥工业大学教授,硕士生导师.

10.3969/j.issn.1003-5060.2017.06.018

TU375.2

A

1003-5060(2017)06-0809-05