数学通报2283号问题的再推广

安徽师范大学数学计算机科学学院 (邮编：241000)

数学通报2283号问题的再推广

安徽师范大学数学计算机科学学院刘其右郭要红(邮编：241000)

《数学通报》2283号问题[1]如下：

设a、b、c>0，求证：

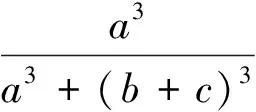
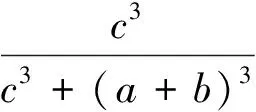
文[2]从指数方面出发，给出了上述一个不等式的推广如下：

定理1若a、b、c>0，且指数α>1，则

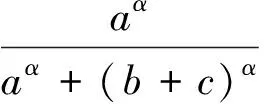
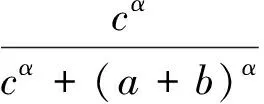
(1)

本文从项数与系数入手，给出定理1的一个推广.

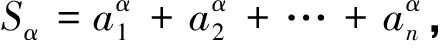
(2)

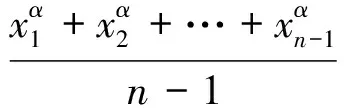
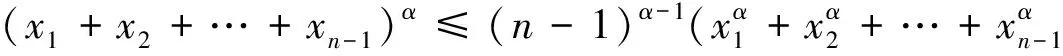
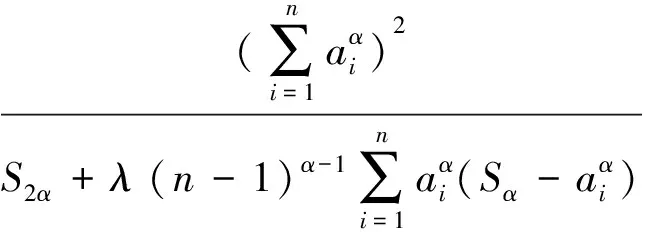
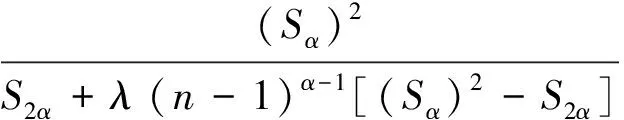
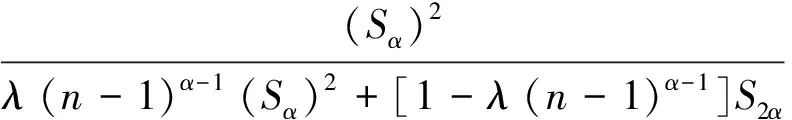
欲证(2)式成立，只须证

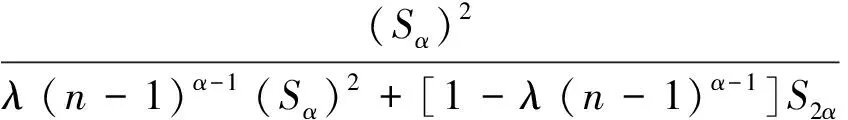
⟺[1+λ(n-1)α](Sα)2≥λn(n-1)α-1(Sα)2+n[1-λ(n-1)α-1]S2α，

⟺n[λ(n-1)α-1-1]S2α≥λn(n-1)α-1(Sα)2-[1+λ(n-1)α](Sα)2，

⟺n[λ(n-1)α-1-1]S2α≥[λ(n-1)α-1-1](Sα)2

(3)

若α=1且λ=1，则(3)为恒等式.

若α>1或λ>1，(3)式等价于

nS2α≥(Sα)2，也即

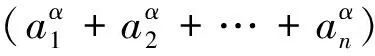
(4)

由加权平均不等式知(4)成立，所以(3)式成立，故(2)式成立，定理2得证.

在定理2中，取n=3,λ=1，则(2)转化为(1)式，所以定理2是定理1的推广.

1 姜坤崇. 问题2283[J]. 数学通报，2016，55(1)

2 黄兆麟. 数学通报2283号问题的指数推广[J]. 中学数学教学，2016(4)：55

3 匡继昌著. 常用不等式(第三版)[M]. 济南：山东科学技术出版社，2004.58

2017-04-11)