探索圈龙图的奇优美性
孙慧,姚兵,2
(1. 西北师范大学数学与统计学院, 甘肃 兰州 730070;2. 兰州交通大学电子与信息工程学院,甘肃 兰州 730070)
探索圈龙图的奇优美性
孙慧1,姚兵1,2
(1. 西北师范大学数学与统计学院, 甘肃 兰州 730070;2. 兰州交通大学电子与信息工程学院,甘肃 兰州 730070)
图的标号是图论的一个重要分支。定义了 2 种新图——圈龙图和多毛圈龙图,并证明它们都具有奇优美标号。多毛圈龙图是通过对圈龙图加叶子得来的,证明他们继承了圈龙图的奇优美性,证明方法能够算法化,为圈龙图和多毛圈龙图应用于网络提供了可行的理论保证。
圈龙图;多毛圈龙图;集有序奇优美标号;奇优美标号;叶子;奇优美图
图论作为数学的一大分支,起源于 1736 年的一个游戏——哥尼斯堡七桥问题。在随后的 300 年间,图论的研究迅速发展壮大,图论的多个分支随之诞生。图的标号作为图论的一个重要分支起源于在 1967 年 Rosa 的一篇论文,他提出了著名而困难的优美树猜想,并在短短的50年间,特别是上世纪六十至八十年代,随着计算机科学的迅速发展和计算机的广泛应用,它的研究发展尤为迅速。如今,图的标号在现代科学技术中的诸多领域(计算机科学、信息科学、密码学、数学证明等等)都得到广泛地应用。在进攻 Rosa 的优美树猜想过程中,许多新的图标号不断被发现,使得图标号成为图论的一个庞大的分支[1- 8]。奇优美标号是图标号的重要种类[9],文献[10-15] 给出关于图的奇优美性的一些结果。本文受文献[8,14]以及环形计算机网络的启发,发现两类具有奇优美标号的新图类——圈龙图和多毛圈龙图。
文中所考虑的图均为有限、无向、简单图。文中没有定义的术语和符号参见文献[15]。为方便起见,用记号 [m,n] 表示集合{m,m+1,m+2,…,n},其中m和n均为非负整数,且满足 0≤m 一个(p,q)-图G是指 |V(G)|=p和|E(G)|=q。图G的一个从顶点集V(G) (或边集E(G),或全集V(G)∪E(G)) 到一个非负正数集的单射f是指任何 2 个不同顶点u,v(或 2 条边或 2 个元素) 的像不同,即f(u) ≠f(v),称f为G的一个标号(labeling)。以下顶点标号集合{f(u)|u∈V(G)} 简记为f(V(G)),边标号集合 {f(uv)|uv∈E(G)} 简记为f(E(G))。 定义 1[14-15]对于给定的(p,q)-图G,如果存在一个单射f:V(G) → [0,q],使得边标号集合{f(uv)=|f(u)-f(v)‖uv∈E(G)}=[1,q],则称f是G的一个优美标号(graceful labeling),也称G为优美图(graceful graph)。此外,若图G是具有顶点二部划分 (X,Y) 的二部图,且f满足max{f(x)|x∈X} 定义 2 对于给定的(p,q)-图G,如果存在一个单射f:V(G) → [0, 2q-1],使得 f(E(G))={f(uv)=|f(u)-f(v)‖uv∈E(G)}=[1, 2q-1]o 则称G为奇优美图(odd-graceful graph),f是G的一个奇优美标号(odd-graceful labeling)。若图G是具有顶点二部划分(X,Y) 的二部图,且f满足f(X) 证明 设f是G的奇优美标号。现定义X={v|f(v) 是偶数},Y={v|f(v) 是奇数}。显然,V(G)=X∪Y以及X∩Y=∅。由于G的每一条边uv的标号为奇数,所以X和Y都是独立集。 其中F(n+1)=0。定义圈龙图G的一个标号函数f如下: f(w)=s-F(1)+2n-3; f(u1,2k-1)=F(2)+2k+2n-4,k∈[1,α(1)] 当i∈[2,n]时, f(ui,2k)=s-F(i+1)-2k+2n-2i+1, k∈[1,α(i)] f(ui ,2k-1) = (i) 任何 2 个顶点的标号互不相同,且对任意顶点u∈V(G),总有f(u)∈[0, 2q-1]。在圈龙图G的头中,k按取值范围取不同值时,圈龙图G上的顶点标号分别为: f(u1,2)=s-F(2)+2n-3,f(u1,4)= s-F(2)+2n-5,…, f(u1,α(1)+1)=s-F(2)+2n-α(1)-2, f(u1,α(1)+3)=s-F(2)+2n-α(1)-6, f(u1,α(1)+5)=s-F(2)+2n-α(1)-8,…, f(u1,a1-2)=s-F(2)+2n-a1-3, f(u1,a1)=F(1)+2n-3,f(w)= s-F(1)+2n-3, 图1 圈龙图Fig.1 A scheme of a cyclic dragon-graph D〈Ci 不难发现,在一个圈龙图G中,不同的顶点ui,j(j=2k或j=2k-1)的标号f(ui,j)彼此互不相同,那么,除了在圈Ci和Ci+1的公共顶点以外,当i从1取到n时,任何两个不同的顶点的标号皆不相同。需要注意的是,2个圈Ci和Ci+1的公共顶点的顶点标号是 此外, 这就证明:当u≠v(u,v∈V(G))时,总有f(u)≠f(v)和f(V(G))⊂[0,2q-1]。 以及 以及 在圈龙图G的头中,当k的取值范围取不同时,圈龙图G上的边标号取值分别为: 当i∈[2,n]时,可计算出圈龙图G上的边ui,juk,l的标号如下: 在圈龙图G中,每一个边标号的值也取决于i和k,在同一个圈Ci上,不同的边ui,jvi,l,当k按取值范围取不同值时,显然边标号f(ui,jvi,l)彼此互不相同。 此外, 另一方面,在圈龙图G的头中,有 因为 综合知:f满足奇优美标号的定义且有f(X) 图2是定理1的一个示例。 定理2 若圈龙图D〈Ci〉n1满足ai≡0(mod 4)(i∈[2,n]),a1≡2(mod 4),那么在其上通过任意加叶子,得到的多毛圈龙图HD〈Ci〉n1是奇优美图。 证明 令 其中 以及顶点标号为g(ui,j)=g(ui)+g(uiui,j)(j∈[1,li],i∈[2,s])。 3) 令g(v1v1,1)=2[M(s)+N(t)]-1,g(v1,1)=g(v1)-g(v1v1,1),定义多毛圈龙图G*的边标号为g(v1v1,l)=g(v1v1,1)-2(l-1)=2(M(s)+N(t))-2l+1(l∈[1,k1]),顶点标号为g(v1,l)=g(v1)-g(v1v1,l)(l∈[1,k1])。最后定义多毛圈龙图G*的边标号 图2 解释定理 1 的一个例子 另外,还有 进一步,有 因为 所以, 因此,当u≠v(u,v∈V(G*))时,总有g(u)≠g(v),以及 多毛圈龙图G*的边标号由 2 部分组成: 和 也就是说, 满足奇优美标号的定义,定理2得证。 解释定理2的一个例子在图3中给出。 图3 解释定理2的一个例子Fig.3 An example for illustrating Theorem 2 本文通过探索圈龙图和多毛圈龙图的奇优美性,定义了两种新图——圈龙图和多毛圈龙图,丰富了图论中奇优美图的种类。定理 1 证明了圈龙图具有集有序奇优美标号,定理2证明了多毛圈龙图具有奇优美标号。但是,进一步研究发现多毛圈龙图则只具有奇优美标号,不再具有集有序的性质。需要注意的是,本文的圈龙图的圈Ci和Ci+1的连接点不能够任意,那么连接点任意的圈龙图的图是否也具有奇优美标号呢? 另外,多毛圈龙图是通过对圈龙图加叶子得来的,并且良好的继承了圈龙图具有奇优美标号的性质,那么这种加叶子的方法是不是可应用于所有的图,并且新图是否依然继承了原图的标号性质,本文的圈龙图是否具有其他有意义的标号,这些都是今后需要继续研究的课题。 [1] 魏丽侠, 张昆龙. 几类并图的优美标号[J]. 中山大学学报(自然科学版), 2008, 47(3):10-13.WEILX,ZHANGKL.Gracefullabelingofseveralclassesofgraphs[J].ActaScientiarumNaturaliumUniversitatisSunyatseni, 2008, 47(3): 10-13. [2] 赵喜杨, 姚兵. 探讨树的(k,d)-边魔幻全标号[J]. 中山大学学报(自然科学版), 2016, 55(6): 67-73.ZHAOXY,YAOB.Discussionon(k,d)-edgemagictotallabeling[J].ActaScientiarumNaturaliumUniversitatisSunyatseni, 2016, 55(6):67-73. [3] 唐保祥, 任韩. 2类优美图的冠的优美标号[J]. 中山大学学报(自然科学版), 2015, 54(5): 24-27.TANGBX,RENH.Gracefullabelingof2kindsofgracefulgraphs[J].ActaScientiarumNaturaliumUniversitatisSunyatseni, 2015, 54(5): 24-27. [4]CHENGH,YAOB,CHENXE,etal.Ongracefulgeneralizedspidersandcaterpillars[J].ArsCombinatoria, 2008, 87: 181-191. [5] 姚明, 姚兵, 赵振学, 等. 关于太阳图魔幻标号的若干结果[J]. 甘肃科学学报, 2015, 27(4): 1-5.YAOM,YAOB,ZHAOZX,etal.Someresultsonthemagiclabelingofthesolargraph[J].JournalofGansuScience, 2015, 27(4): 1-5. [6] 刘信生, 刘元元, 姚兵, 等. 龙图的优美性[J]. 兰州理工大学学报, 2013, 39(3): 133-135.LIUXS,LIUYY,YAOB,etal.Thegracefulnessofdragongraph[J].JournalofLanzhouUniversityofTechnology, 2013, 39(3): 133-135. [7] 王宏宇, 姚兵, 杨超. 一类特殊对称图的边魔幻性[J]. 四川师范大学学报(自然科学版), 2013, 36(1): 28-33.WANGHY,YAOB,YANGC.Edgemagicofaclassofspecialsymmetricgraphs[J].JournalofSichuanNormalUniversity(NaturalScienceEdition), 2013, 36(1): 28-33. [8]FUMY,LIUXD,WANGLG.Thegracefulpropertyofakindofstringgraphs[J].JournalofSouthwestUniversityforNationalities, 2005, 31 (6):843-851. [9]GANAJOTHIRB.Topicsingraphtheory[D].Madurai:MaduraiKamarajUniversity, 1991. [10] 姚兵, 张家娟, 郭璟霞. 复合毛毛虫树的优美及奇优美性[J]. 兰州理工大学学报, 2012, 38(4): 147-150.YAOB,ZHANGJJ,GUOJX.Thegracefulandoddgracefulnessofthecompoundcaterpillartree[J].JournalofLanzhouUniversityofTechnology, 2012, 38(4): 147-150. [11] 谢建民, 姚兵, 张锐. 两类圈相关图的奇优美标号[J]. 甘肃科学学报, 2013, 25(4):1-3.XIEJM,YAOB,ZHANGR.Oddgracefullabelingoftwoclasscirclecorrelationgraphs[J].JournalofGansuScience, 2013, 25(4): 1-3. [12] 刘信生, 刘元元, 姚兵, 等. 具有奇优美性的一类龙图[J]. 西南大学学报(自然科学版), 2014, 36(4): 47-51.LIUXS,LIUYY,YAOB,etal.Aclassofgraphswithoddgracefulness[J].JournalofSouthwesternUniversity(NaturalScienceEdition), 2014, 36(4): 47-51. [13] 严谦泰. 积图Pn×Pm的奇优美性和奇强协调性[J]. 系统科学与数学, 2010, 30(3): 341-348.YANQT.ProductPn×Pmoddgracefulandoddstronglyharmonious[J].SystemScienceandMathematics, 2010, 30(3): 341-348. [14]ZHOUXQ,YAOB,CHENXE,etal.Aprooftotheodd-gracefulnessofalllobsters[J].ArsCombinatoria-WaterloothenWinnipeg-, 2012, 103:13-18. [15]JOSEPHAGALLIAN.Adynamicsurveyofgraphlabelling[J].TheElectronicJournalofCombinatorics, 2013,14:DS6. Exploring the odd gracefulness of cyclic-dragon graphs SUN Hui1, YAO Bing1,2 (1. College of Mathematics and Statistics, Northwest Normal University, Lanzhou 730070, China;2. School of Electronic and Information Engineering, Lanzhou Jiaotong University, Lanzhou 730070, China) The labeling of Graph is an important branch of the graph theory. Two kinds of new graphs, cyclic-dragon graphs and haired cyclic-dragon graphs, are defined. It is proved that they are odd-graceful. The haired cyclic-dragon graphs is made by adding leaves to cyclic-dragon graphs, so they inherit the odd-graceful property of cyclic-dragon graphs, whose method can algorithm that may be a theoretical guarantee for applying cyclic-dragon graphs and haired cyclic-dragon graphs to network. cyclic-dragon graphs; haired cyclic-dragon graphs; set-ordered odd-graceful labeling; odd-graceful labeling; leaf; odd-graceful graph 10.13471/j.cnki.acta.snus.2017.04.002 2016-12-16 基金项目:国家自然科学基金(61163054, 61363060, 61662066) 孙慧(1992年生),女;研究方向:图着色与标号;E-mail:18919104606@163.com 姚兵(1956年生),男;研究方向:图着色与标号、复杂网络及优化;E-mail:yybb918@163.com O157.5 A 0529-6579(2017)04-0009-07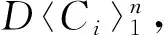
1 主要结论
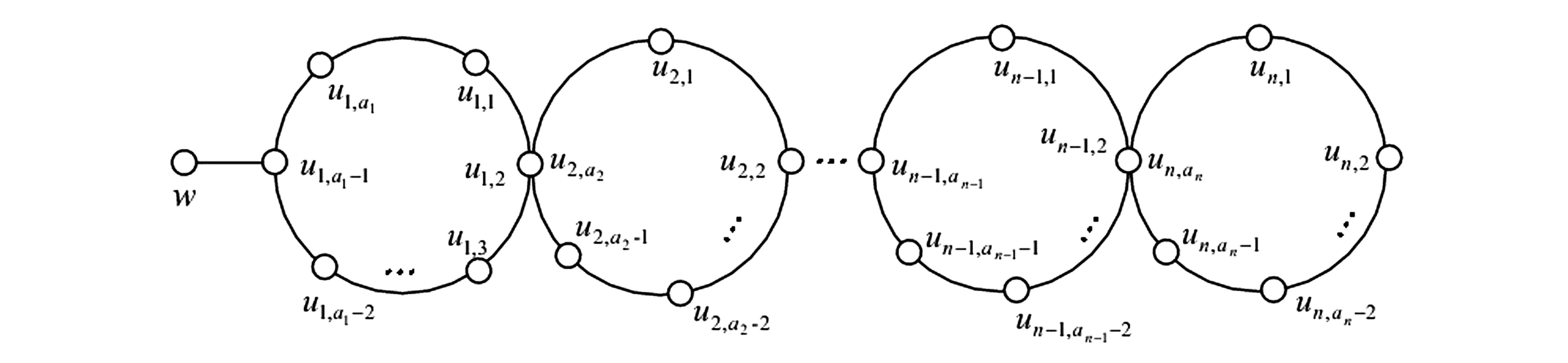


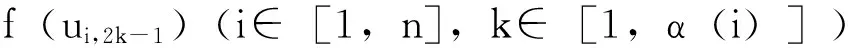
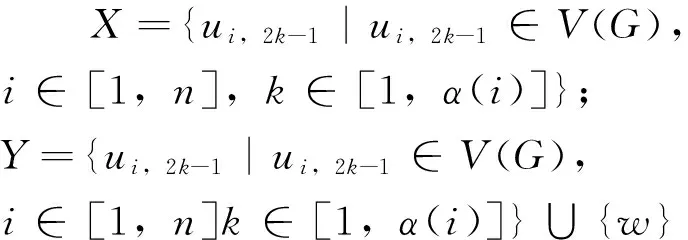
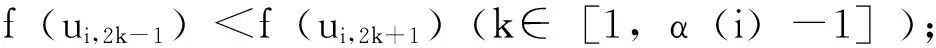


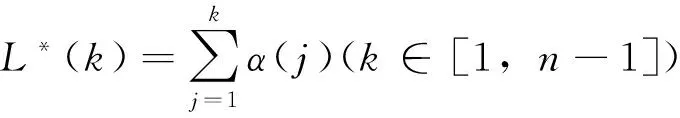
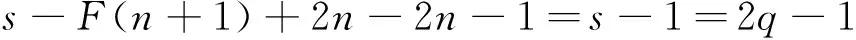
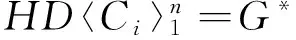
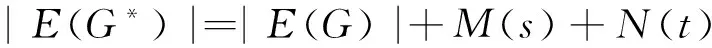
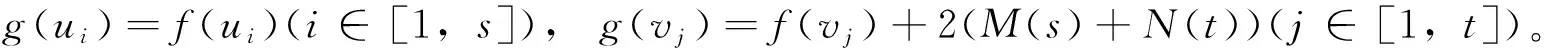
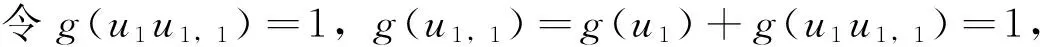
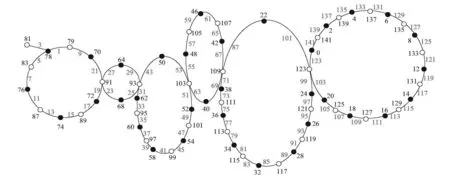
Fig.2 An example for illustrating Theorem 1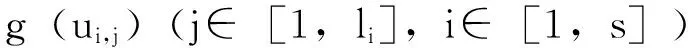

2 总结与问题

