资本资产定价模型在上海A股市场的检验
聂高辉 蔡琪
资本资产定价模型自上世纪60年代提出以后一直在资产评估、风险把控以及资产合理分配等领域受到广泛的关注与使用。该模型可以很好的辨别股市中某支股票或者某个证券的价格是否合理,同时通过模型的β系数的变化来衡量市场对资产的敏感度,从而有效的规避风险,使收益最大化。
国外对于资本资产定价模型的研究比较早,现今已经形成了一套完备的体系。资本资产定价模型自推导公布以来由一开始的推崇到质疑,到最后的扩充与发展。Jensen(1972)将资本资产定价模型运用到实务中,并且取得了预期的效果,进一步证明了该模型适合财务分析。资本资产定价模型在上世纪70年代到90年代受到了巨大的质疑与挑战,Ball(1978)实证分析发现股价收益比例高的企业往往会获得更高的回报,而且他认为这并非市场的原因,而是模型本身的缺陷导致的。Jegadeesh(1993)也提出了疑问,他发现股票的收益具有一定的惯性,会受前期的影响,他把这一现象定为“惯性效应”。在争论的同时Merton(1973)将资本资产定价模型由静态推广到动态,后来的学者在此基础上逐步建立了套利定价理论。国内对于资产资产定价模型的研究主要集中在分析其理论是否适用于我国上交所和深交所的股票市场。马静如(2001)运用动态分组方法分析深圳证券交易所A股市场是否适用CAPM模型,研究表明β系数与超额收益率并不成正比,小公司效应非常普遍,CAPM模型并不适合深圳证券交易所的股票市场。聂高辉、陈黎明(2015)选取深圳证券交易所A股市场为实证对象,对1300支股票进行分组研究,发现基本符合资本资产定价模型的理论,但是市场投机性仍存在。
国内外对于资本资产定价模型的研究还存在许多争论,争论点主要在实用性方面,CAPM模型是单期模型,需要许多约束条件。国内对于深圳证券交易所股票市场资本资产定价模型的适应性研究比较透彻,对于上海证券交易所股票市场的研究还比较少。尤其是在上海证券交易所在注册制改革,引入创业板和产业板后的股票市场的研究更少。文章选用上海证券交易所2015年3月到2017年1月1000支股票的数据进行模型的适用性分析。
本文选取沪市股票进行实证分析,我们以2015年3月作为基期,采集2015年3月至2017年1月以来23个交易月交易数据,数据来源于wind咨询金融终端;收集的数据对象主要有:交易日期、开盘价、收盘价、成交量、成交金额。
一、模型构建
考虑到模型研究的是股票组合收益率,假定某支股票α和股票市场χ一起构成了股票组合,组合股票的收益率表达式为式(1),方差表达式为式(2)。
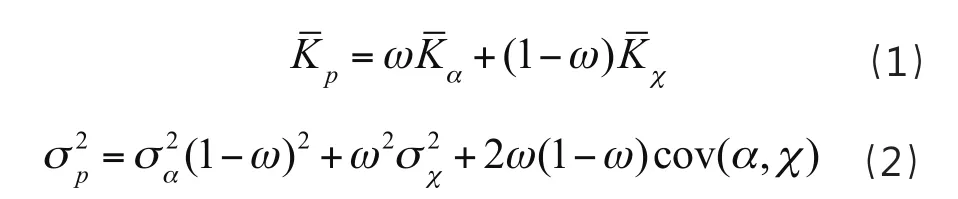
式(1)和式(2)中加入了ω和(1-ω),分别代表股票α和股票市场χ各自的权重系数。分别代表股票a的收益率和方差,分别代表股票市场的平均收益率和方差,分别代表股票组合α的收益率和方差,cov(α,χ)代表两者的协方差。
从上述两个方程式可以看出,权重对于两者均具有作用,因此我们对式(1)和式(2)的权重项进行一阶求导,得到式(3),在式(3)的基础上进行变化得到式(4)。
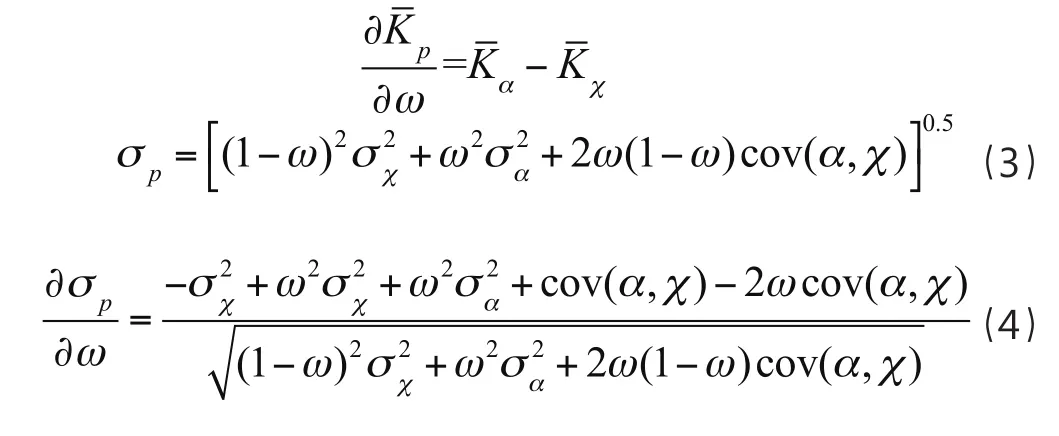
当权重趋近于零时,股票的组合收益率将无限趋近于市场的平均收益率,同时股票的组合方差也将无限趋近于市场的平均方差。因此式(4)可以理解为式(5)。同时,无风险收益Kf与市场平均收益所形成的线性方程的斜率可以表示为式(6)
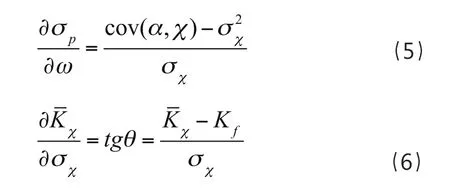
整理式(3)到式(6)可以得到资本资产定价模型的一般表达式为式(7)。
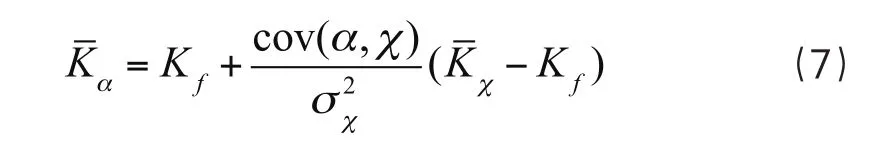
式(7)中Kf代表的是股票的无风险收益;代表的是个别股票的风险补偿;就是股票的贝塔系数,也是衡量股票风险的系数。因此,通常的CAPM模型方程表达为式(8)。
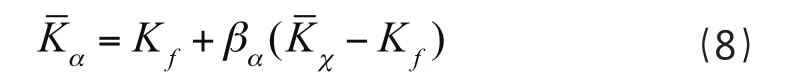
二、上海股市检验分析
CAPM模型的假设主要有两点。其一,股票组合的平均超额收益率与β系数之间存在线性关系;其二,CAPM模型中股票组合的超额收益率只与系统风险有关联。检验该模型在上海股票市场的适用性需要在这两个方面作出考虑。
(一)线性关系检验
在检验线性关系前,需要确定几个数据。模型中的无风险收益率按照2015年发行的3年期国债利率5%计算,股票的收益率按照当期收盘价与前期收盘价的差与前期收盘价的比值计算,股票组合的收益率按照组合中所有股票的平均收益率计算。同时,考虑到上海股市的股票数量较多,为保证模型验证的准确性以及确保选择的股票能够代表上海股市,选择上海证券交易所发行的具有代表性的800支股票,借鉴Jensen(1972)动态分组的办法,将800支股票按风险系数大小分成40组,每组20支股票。运用式(8)给出的方程式计算出40组股票组合的风险系数β。CAPM模型简化为一般的表达式为式(9),其中Ri表示第i个股票组合的超额收益率,将计算出来的组合收益与组合风险的数据代入,得出的回归结果如表1所示。
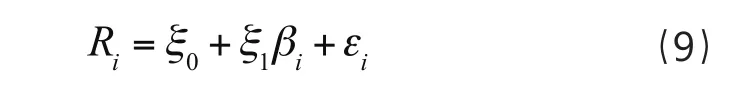
从式(9)的回归结果(表1)可以看出,模型的拟合系数为0.563,大于0.5说明该模型可以比较好的解释40组股票组合的超额收益率与风险系数β之间的关系。回归方程的常数项ξ0值为-0.798,且该系数在100%置信区间可信,这说明当系统的风险系数趋于零值时股票组合的超额收益率为负数,也就是说这种情况下股票组合没有收益,并且会亏损。这也从侧面反映出上海股市的投资者中风险偏好者较多,过于寄希望于高风险股票组合的高收益回报。风险β与超额收益率之间的系数ξ1值是0.031为正数,而且该系数在100%的置信区间内可信,这也表明上海股市中风险与超额收益存在明显的正向关系,这点和CAPM模型的第一点假设基本吻合。
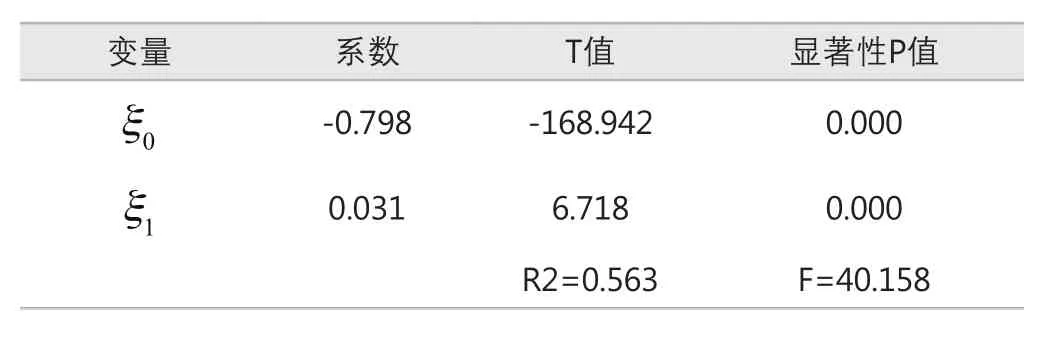
表1 回归结果
(二)横截面检验
模型检验的第二个假设就是超额收益率只与系统风险有关系。因此,文章在式(9)基础上引入非系统风险项δ以及风险系数β的二次方项β2检验这两项是否会影响股票组合的超额收益率,得到变化后的模型形式为式(10),代入相应数据得到回归结果(表2)。
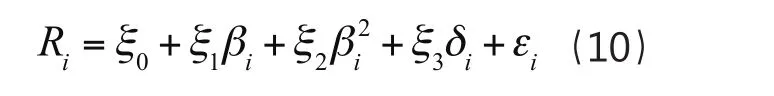
从式(10)的回归结果(表2)可以看出,模型的拟合系数为0.506,大于0.5说明该模型能较好的解释这四个变量之间的关系。变量ξ0的系数值为-0.741,且该系数值在100%的置信区间可信,负值也再次印证上海股票市场的投资者喜好风险投资。变量ξ1的系数值为0.028,且该系数值在99%置信区间可信,正值也说明上海股市的股票超额收益与风险系数存在正向关系。变量ξ2与ξ3的显著性P值为0.125和0.227均大于0.1,说明这两个系数值不显著,为增加模型的可信度,可以将这两个变量去除。另外,将式(9)和式(10)的回归结果比较发现,加入这两个变量后,模型的拟合优度降低了,AIC值也变大了。因此,可以认为非系统风险项δ以及风险系数β的二次方项β2与超额收益没有关系。
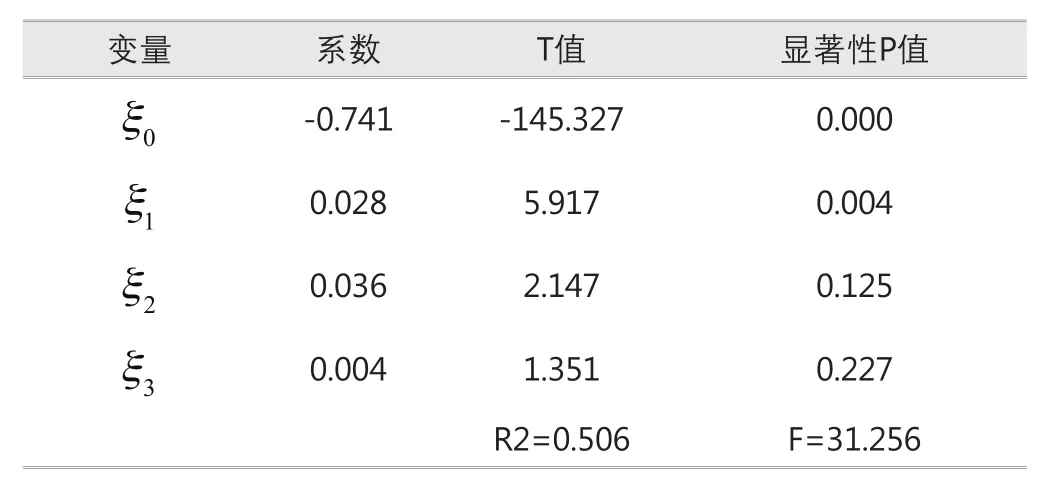
表2 回归结果
三、结论建议
文章首先介绍了资本资产定价模型的理论基础与模型方程,然后选取上海股市作为研究对象,检验该模型是否适合上海股票市场,研究结果表明上海股市的风险系数与超额收益存在正向关系,而且上海股市的风险系数β已经涵盖了所有影响股市超额收益的因素,超额收益的变化与其他任何要素都不相关。这两点与资本资产定价模型的一般理论非常符合。另外,模型(9)和模型(10)的常数项均为负值,表明上海股市的投资者偏爱风险收益,投机行为较多,股市发展还不成熟。
上海股市在进行注册制改革,引入创业板和产业板后股票市场越来越向着规范化发展,但仍然存在一些不足。首先,上海股票市场的投资者不够理性,过于追求风险收益,这和资本资产定价模型的投资者均为风险厌恶者的基本设定不一样。过于追求风险收益增加了股票市场的投机性,不利于股票市场的稳定发展。其次,市场信息发布不及时、不透明,投资者不能及时理解市场行情。同时,监管不到位,股票市场仍然存在主体企业财务造假的可能性。
针对上述问题,文章提出两点建议促进上海股市健康有序的发展。第一,建立股票市场准入机制,规范投资者的投资行为,政府部门应当进行入市前对投资者进行相关专业知识的普及与教育,同时积极引导投资者理性投资,避免投资的盲目性。第二,建立高效透明的信息发布平台,加强市场监管力度。交易所应当避免延时信息与错误信息出现,且股市信息要做到及时透明,杜绝信息不对称投资行为。

