快速响应微小卫星发射时机分析
李 岩 蔡远文 赵征宇 邓小军
1.装备学院航天装备系,北京101416 2.酒泉卫星发射中心,酒泉732750
快速响应微小卫星发射时机分析
李 岩1蔡远文1赵征宇2邓小军2
1.装备学院航天装备系,北京101416 2.酒泉卫星发射中心,酒泉732750

为了研究应对突发事件的对地观测微小卫星应急快速发射和部署问题,综合运用二体动力学模型和球面几何学相关知识,分析了固定发射和机动发射方式下微小卫星发射时机的选择方法。根据在规定时刻从指定轨道过顶确定目标的总体要求,提出了满足平面窗口和相位窗口条件的发射时机和发射位置计算方法。该方法能应用于微小卫星快速部署相关问题的仿真试验,为研究航天发射系统的快速响应机制提供了理论支撑。 关键词 微小卫星;轨道;发射窗口;幅角;对地观测
微小卫星集成了微纳米、微机电等先进技术和工艺,相比同等功能的大型卫星,具备体积轻便、发射灵活和响应敏捷等优势。在应对突发事件时,已在轨运行的大卫星,往往难以及时变轨获取事发区域的信息。这时,机动灵活地快速发射微小卫星进入指定轨道,能够及时、准确地提供目标区域的观测信息,有效弥补在轨卫星时隙,为快速行动决策提供情报支持。在卫星轨道参数明确的条件下,发射时机的选择是决定微小卫星的响应是否迅速及时的关键因素。关于发射时机或发射窗口的计算,许多文献都有论述,文献[1-3]对发射窗口的概念、影响因素和计算过程等给出了理论阐述,但没有设计针对具体任务的算例。文献[4-6]分别对星地链路时间窗口、交会对接发射窗口和再入返回窗口进行计算和仿真,均针对预定常规发射和返回任务,发射窗口主要关注航天器光照、导航条件和机动能力,对在规定时间到达指定位置的应急性要求不高。文献[7-8]分析了平面和相位窗口,给出了轨道机动和交会任务发射窗口的快速确定方法,对对地观测任务发射窗口的分析具有一定参考意义。本文借鉴上述文献的理论和方法,在目标点位置、运行轨道和过顶时间确定的条件下,分析微小卫星快速发射时机,为对地观测微小卫星的快速部署提供决策支持。
1 发射窗口选择问题分析
针对确定区域的对地观测,要求在最短时间内将微小卫星发射进入指定轨道,并在规定时刻t1到达目标区域上空执行观测任务。设目标地区经纬度为λ1,φ1,发射点经纬度为λ0,φ0。观测轨道一般选取近地圆轨道,设轨道高度为h,倾角为i,升交点赤经为Ω,可采用固定点发射和机动发射的发射方式。
对于固定点发射的时机选择,一方面要求发射点经过指定轨道平面,即满足平面窗口[9-10]条件;另一方面,卫星发射进入轨道后需要在规定时刻t1过顶目标区域,即满足相位窗口[9-10]条件。如果发射运载器的上面级变轨能力较强,能够搭载微小卫星完成轨道平面内的相位调整后释放,使其在t1时刻过顶目标区域;或者微小卫星自身可机动调整相位,确保在t1时刻过顶目标区域,那么发射窗口的选择可以只考虑平面窗口条件,而相位调整则由上面级或微小卫星自身机动完成。如果不具备上面级,微小卫星也不具备调相机动能力,那么就要计算合适的发射时机,使卫星入轨时,既满足平面窗口条件,又满足相位窗口条件。
在机动发射条件下,假设运载器可以机动至地面任意发射点发射卫星(如:空中机动发射),那么确定应急发射时机的问题,可以转化为选择合适的发射位置,使卫星在规定时间tr内过顶目标区域。这样,发射时刻即为t1-tr,发射点位置则需按照平面和相位窗口条件确定。
综上分析,对地观测微小卫星发射时机选择可分为以下3种情况分析:
1)固定发射点,考虑平面窗口条件的发射窗口选择,相位调整由上面级或微小卫星自身机动完成;
2)固定发射点,考虑平面和相位窗口条件的发射时机选择,使卫星入轨时,既满足平面窗口条件,又满足相位窗口条件;
3)机动发射条件下的发射位置选择,根据平面和相位窗口条件以及时限tr计算确定。
2 考虑平面窗口条件下的固定点发射
时机选择
图1给出了在卫星过顶目标点时刻t1时,地球球面、发射点纬线圈、赤道圈以及卫星轨道平面和地球球面交线圈之间的相互关系。发射点A的经纬度为A(λ0,φ0),目标点C的经纬度为C(λ1,φ1)。B点为地球球面上与发射点A纬度相同的纬线圈与卫星轨道平面的交点,D点为过发射点A的经线与赤道的交点,H点为卫星轨道平面与赤道圈的交点,F点为过目标点C的经线与赤道的交点,G点为过B点的经线与赤道的交点。
假设轨道平面在惯性空间保持不变,对于纬度小于给定轨道和赤道平面夹角的固定发射点,每个恒星日内有2次经过给定轨道平面的时刻,即有2个发射窗口,可分别采用升轨和降轨的发射方向将卫星发射入轨。可依据任务时间响应需求、天气条件等因素进行综合考虑,选择适合的发射窗口。以升轨发射为例,当发射点A随地球自转至B点时,发射运载器才能将卫星发射至指定观测轨道,发射弹道在轨道平面内。设最近一次发射窗口t0距t1时刻之前Δt,即Δt=t1-t0,此时发射卫星满足平面窗口条件,而相位调整则由上面级或微小卫星自身机动完成,调整时间设为tp。设地球自转角速度ωE=360/86164((°)/s),计算t0的过程如下。
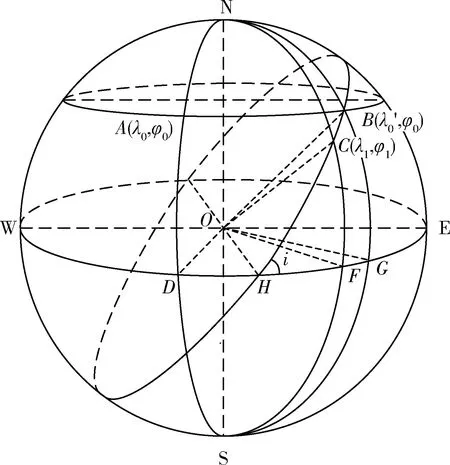
图1 固定点发射时的球面几何关系
如图1所示,在球面三角形ΔCHF中,边CH对应的地心角∠COH可由球面三角正弦公式计算得到:


(1)
由球面三角形边余弦公式,可得地心角∠HOF:
cos∠COH=cosφ1cos∠HOF+
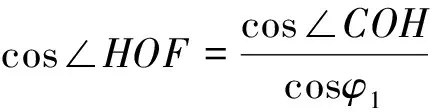

(2)
地心角∠HOF就是H点与F点在地球球面上的经度差,也是H点与C点的经度差。这里∠HOF和∠COH的符号和象限一致。
同理,选取球面三角形ΔBHG,可以计算得到地心角∠BOH:

(3)
图1中,升轨发射时可取∠BOH<90°。利用球面三角形边的余弦计算得到地心角∠HOG:
cos∠BOH=cosφ0cos∠HOG+
sinφ0sin∠HOGcos90°

(4)
地心角∠HOG是H点与G点在地球上的经度差。
由赤道平面内角的几何关系,得到C点与B点的经度差∠FOG:
∠FOG=∠HOG-∠HOF
(5)
t1时刻,D点与发射点A在同一条经线上,两者具有相同的经度λ0;F点与目标点C在同一条经线上,两者也具有相同的经度λ1。因此,赤道平面内可以得到D点与F点的经度差:
∠DOF=λ1-λ0
(6)
在赤道平面内根据角的几何关系,A点和B点的经度差∠DOG:
∠DOG=∠DOF+∠FOG
(7)
由上述计算过程可知,升轨发射时,从卫星发射到过顶目标区上空这段时间内,发射点随地球自转转过的经度为:
Δλ=360°-∠DOG
(8)
经历的时间为:
(9)
则最近一次升轨发射时间t0=t1-Δt。
上述发射窗口满足平面窗口条件,经过上升段飞行时间th,卫星入轨,再经过相位调整时间tp,微小卫星才能在规定时刻t1过顶目标区域。假设轨道平面在惯性空间保持不变,如果t1≥t0+th+tp,则发射窗口t0满足任务需求;若t1 同理可以推导得到,采用降轨发射入轨时,从发射点发射到卫星过顶目标区上空,发射点随地球自转转过的经度为(角度仍为图1中角度大小): Δλ′= 360°-[∠DOF-∠HOF+180°-∠HOG] (10) 经历时间为: (11) 则最近一次降轨发射时刻t0′=t1-Δt′。 选择合适的发射时机,可以使卫星发射入轨时既满足平面窗口条件,又满足相位窗口条件。由第2节的条件和计算结果可知,在升轨发射时,发射窗口t0N必须满足的平面窗口条件为: t0N=t1-Δt-N·TE (12) 其中,N≥0,且为整数。此时还要满足相位窗口条件,才能确保在t1时刻过顶C点。相位窗口条件可在卫星轨道平面内分析,如图2所示。 图2 升轨发射轨道平面俯视图 图3 降轨发射轨道平面俯视图 图2为升轨发射时,从轨道平面法线方向向下俯视图。与图1定义相同,B点为平面窗口条件下的发射点,C点为t1时刻目标点及卫星所在位置的星下点。假设卫星入轨前轨道上有一满足相位窗口条件的虚拟卫星,则发射过程相当于发射追踪航天器与虚拟卫星交会,使交会时两航天器的轨道参数完全相同。设卫星发射后经过th至入轨点K,划过地心角∠BOK=θ。L为发射时刻t0虚拟卫星所在位置,满足以下条件: ∠LOK=αs=th·ωs (13) 其中,ωs为卫星轨道角速率(单位:(°)/s),可由卫星轨道参数求得。从卫星过顶C点回退至卫星发射时刻,经历时间Δt+N·TE,此时卫星(虚拟卫星)位置在L,即为相位窗口条件。相对于射线OC进行角度计算,设顺时针为正方向,位置L在轨道平面内相对于C点的幅角∠LOC为: ∠LOC=(Δt+N·TE)·ωs-360°·k (14) 其中,k≥0,且为整数,使∠LOC∈[0°,360°)。 再由轨道平面内角度几何关系: ∠LOC=αs-θ-∠BOC =αs-θ-(∠BOH-∠COH) (15) 式(14)和(15)构成了升轨发射时的相位窗口条件,在指定的误差范围内,求得满足条件的最小正整数N,即可得到平面和相位条件均满足的发射时机为: t0N=t1-Δt-min(N)·TE (16) 如图3,同理可得降轨发射的相位窗口条件为: ∠LOC=(Δt′+N·TE)·ωs-360°·k (17) ∠LOC=360°+αs-θ- (18) 其中,取∠LOC∈[0°,360°)。 若运载器载体可以在任意发射点机动发射卫星,那么应对突发情况时,能够在指定时限tr内发射微小卫星进入指定轨道,并在规定时刻t1到达目标区域C(λ1,φ1)上空,只需要根据任务要求确定机动发射点B的位置(λ0,φ0)即可实施发射,发射时刻可定为t1-tr。 发射点位置由平面和相位窗口条件确定。如图4所示,设B为发射点,K为入轨点,D为过B点经线圈与赤道交点,L为虚拟卫星在发射时刻所在位置。C′点为升轨过顶条件下,在发射时刻目标点所在纬度圈与卫星轨道平面的交点,F为过C′点经线圈与赤道交点。显然,C′点此时的经纬度(λ1′,φ1′)分别为: (19) 图4 机动发射时刻球面几何关系 从卫星过顶目标点回退至卫星发射时刻,经历时间tr,此时L在轨道平面内相对于C′点的幅角∠LOC′为: ∠LOC′=tr·ωs-360°·k (20) 其中,k≥0,且为整数,使∠LOC∈[0°,360°)。 再由轨道平面内角度几何关系,可得到发射点B在轨道平面内相对于C′的幅角: ∠BOC′=∠LOC′-(αs-θ) (21) 在球面三角形ΔFHC′运用正弦定理得: (22) 根据球面三角形边的余弦公式,可以计算得到地心角∠HOF: cos∠HOC′=cosφ1cos∠HOF+ sinφ1sin∠HOFcos90°⟹ (23) 此处,在顺行轨道升轨侧,相对射线OH的幅角取顺时针方向为正。在球面三角形ΔDHB运用正弦定理得: ⟹φ0=-arcsin(sini·sin∠HOB) (24) 由∠HOB=∠BOC′-∠HOC′,则可得发射点纬度为φ0。 计算得到地心角∠HOD: cos∠HOB=cosφ0cos∠HOD+ sinφ0sin∠HODcos90° (25) 根据B点与C′点的经度差,可得到发射点经度λ0为: (26) 目标C点(133.15°E,26.49°N)出现紧急情况,要求对地观测卫星在XX年10月10日07:11:16,在轨道高度为300km,轨道倾角为63°的圆轨道,过顶C点。固定发射点位置为A(86.06°E,41.68°N)。卫星从发射点到入轨点上升时间为th=636.490s,弹道划过的地心角为θ=4.3938°,采取降轨发射方式。入轨后相位调整时间为48h。限于篇幅,仅给出计算结果:仅考虑平面窗口条件时,发射窗口计算结果为在已知过顶条件时间之前77830s(21小时37分钟10秒),即10月9日09:34:06,考虑相位调整时间为48h,最近发射窗口需在此基础上提前2个恒星日,即10月7日09:41:58。 考虑平面和相位窗口条件时,卫星入轨即进入所需相位,则发射窗口为在已知过顶条件时间之前1456400s(16天20小时33分钟20秒),即9月21日10:37:56。 若采取机动发射,要求在30min(1800s)前发射卫星,发射窗口为10月10日06:41:16,发射点位置B计算结果为(96.2164°E,44.1928°S)。 综合运用二体动力学地球模型和球面几何学相关知识,分析了固定发射和机动发射方式下,应对突发事件的微小卫星发射时机的选择方法。根据在规定时刻、从指定轨道和过顶确定目标的条件,提出了满足平面窗口和相位窗口条件的发射窗口和发射位置计算方法。该方法能应用于微小卫星快速部署相关问题的仿真试验,快速确定应急发射任务的发射时机,为研究航天发射系统的快速响应机制提供理论支撑。本文的研究适用于航天发射任务模拟试验的发射时机快速计算,还需进一步分析精确轨道和地球模型条件下多变量变化对发射时机的影响等问题。 [1] 王家松,祝开建,胡小工.卫星轨道——模型、方法和应用[M].北京:国防工业出版社,2012. [2] 陈克俊,刘鲁华,孟云鹤,等. 运载火箭飞行动力学与制导 [M]. 北京:国防工业出版社,2014. [3] 崔吉俊,等. 航天发射试验工程[M].北京:中国宇航出版社,2010. [4] 李冬,易东云,罗强. 基于J2项摄动的星地链路时间窗口快速算法[J].航天控制,2010,28(1):27-31.(Li Dong,Yi Dongyun, Luo Qiang. A Fast Algorithm for Calculation of the Time Windows between Satellite and Ground Station with J2 Perturbation[J]. Aerospace Control, 2010,28(1):27-31.) [5] 李革非,陈莉丹,唐歌实,张丽艳. 多约束交会对接发射窗口的分析和规划[J]. 宇航学报,2011,32(11):2463-2470.(Li Gefei,Chen Lidan, Tang Geshi, Zhang Liyan. Analysis and Programming of Rendezvous Launch Window with Multi-Constraints[J]. Journal of Astronautics, 2011,32(11):2463-2470.) [6] 王献忠,汤敏兰,张丽敏,刘禹. 再入返回离轨时机及制动策略[J].航天控制,2016,34(4):53-58.(Wang Xianzhong,Tang Minlan ,Zhang Limin ,Liu Yu.Deorbit Times and Braking Strategy for Reentry Vehicle[J]. Aerospace Control, 2016,34(4):53-58.) [7] 李九人,李海阳,蒋自成. 空间救援发射窗口分析[J].国防科技大学学报,2008,30(1):10-14.(Li Jiuren,Li Haiyang,Jiang Zicheng. The Analyze of the Launch Window for Space Rescue Mission[J]. Journal of National University of Defense Technology, 2008,30(1):10-14.) [8] 王雪瑶,龚胜平,李俊峰,等. 基于快速交会特殊点变轨策略的航天器发射窗口分析[J]. 载人航天,2015,21(6):553-559.(Wang Xueyao,Gong Shengping,Li Junfeng, et al. Analysis of Launch Window in Short Rendezvous Mission Transferred at Special Points[J]. Manned Spaceflight,2015,21(6):553-559.) [9] 夏南银. 航天测控系统[M].北京:国防工业出版社,2000. [10] 章仁为.卫星轨道姿态动力学与控制[M].北京:北京航空航天大学出版社,1998. Launch Timing Analysis for Micro-Satellite Responsive Deployment Li Yan1, Cai Yuanwen1, Zhao Zhengyu2, Deng Xiaojun2 1. Department of Space Equipment, Equipment Academy, Beijing 101416, China 2. Jiuquan Satellite Launch Center , Jiuquan 732750, China Focusingontheemergencyofearthobservationmicro-satelliteresponsivelaunchanddeployment,thelaunchtimingselectionmethodoffixedandmaneuverablelaunchingareanalyzedinthispaperbyusingtwo-bodymodelandsphericalgeometry.Analgorithmforcalculatingingthelaunchtimingandpositionisrepresentedbyfittingtheplaneandphasewindowinordertomakethesatellitegetoverthetopoftargetpositionthroughacertainorbitatacertaintime.Thismethodcanbeusedinthemicro-satelliteresponsivedeploymentdemonstrationtestandtheoreticallysupporttheresearchofresponsivespacelaunchsystem. Micro-satellite;Orbit;Launchwindow;Argument;Earthobservation 2017-03-09 李 岩(1981-),男,河南许昌人,博士,讲师,主要研究方向为自动化测试与控制;蔡远文(1967-),男,四川彭州人,博士,教授,主要研究方向为飞行器总体技术;赵征宇(1990-),男,浙江金华人,硕士,助理工程师,主要研究方向为兵器科学与技术;邓小军(1980-),男,四川威远人,学士,工程师,主要研究方向为飞行器测试与控制。 V525 A 1006-3242(2017)03-0067-063 考虑平面和相位窗口条件的固定点发射时机选择
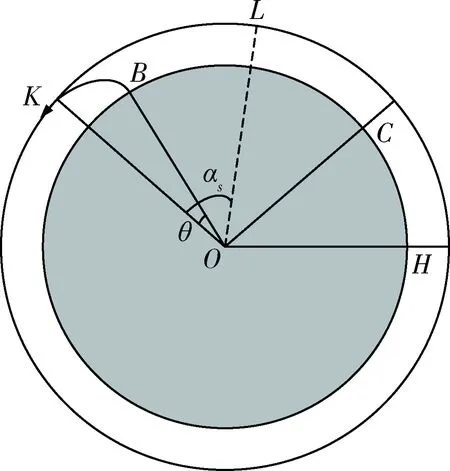
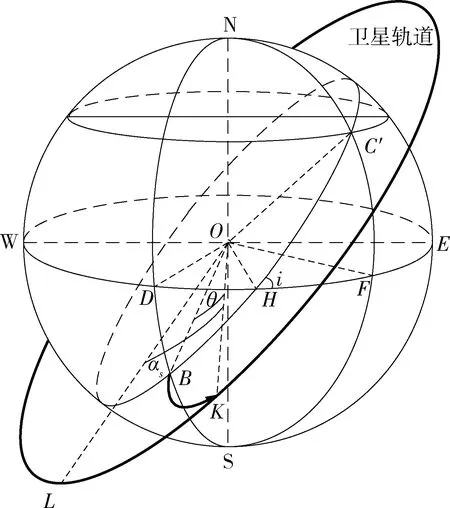
4 机动发射条件下的发射位置选择
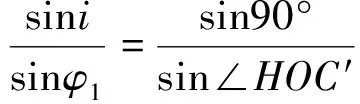

5 算例
6 结论

