碰撞角约束的全向拦截制导律研究

白国玉， 沈怀荣， 闫 梁， 李 辕

(1. 装备学院 研究生管理大队, 北京 101416； 2. 装备学院 航天装备系, 北京 101416； 3. 北京跟踪与通信技术研究所， 北京 100094)

碰撞角约束的全向拦截制导律研究

白国玉1， 沈怀荣2， 闫 梁3， 李 辕3

(1. 装备学院 研究生管理大队, 北京 101416； 2. 装备学院 航天装备系, 北京 101416； 3. 北京跟踪与通信技术研究所， 北京 100094)

针对空间拦截制导律设计中的碰撞角约束问题，通过在全向真比例制导律中增加并实时求解时变偏置角速率的方法，设计了带约束碰撞角的全向真比例制导律(Angle-Constraint Omnidirectional True-Proportional Navigation，AC-OTPN)，解决了顺、逆轨拦截模式下对末端碰撞角的切换、装订和控制问题。该制导律能根据目标和拦截器的运动关系自主选择顺轨或逆轨拦截模式并装订末端碰撞角进行拦截制导，碰撞角控制精度高。AC-OTPN可通过调整理想的末端碰撞角以增强碰撞效能，使得相对质量、体积较小的拦截器同样具备较强的毁伤能力，为拦截器的小型化设计和携带更多的子拦截器提供技术支撑。

碰撞角；约束；全向；拦截；制导律

拦截制导的首要目的是确保满足目标杀伤对于最终脱靶量的要求，然而随着拦截技术的发展和作战要求的变化，很多拦截任务不但要求精确命中，而且对末端碰撞角度[1-2]提出要求，以获得更好的攻击效果。碰撞角约束制导律的研究理论基础通常为改进型比例制导、最优化或变结构控制理论：Kim等[3]设计了满足静止和低速目标拦截中末端碰撞角约束的时变偏置比例导引制导算法；Ratnoo等[4-5]使用分段比例(Proportional Navigation，PN)制导方案攻击静止目标，通过在不同阶段使用不同的比例系数来达成期望的末端拦截碰撞角；Erer等[6]同样基于分段制导思想，分别使用偏置比例(Bias Proportional Navigation，BPN)与PN制导达成期望的末端碰撞角；Zarchan[7]提出带角度约束的最优制导律(称为“弹道成型制导律”)。带碰撞角约束的高速目标拦截制导律研究较少：Shima和Golan[8-9]提出了带有碰撞角约束的顺轨滑模制导律；胡锡精等[10]设计了基于几何法的拦截匀速运动目标的终端角度约束制导律；闫梁等[11]设计了具备角约束能力的联合偏置比例制导律，拦截大气层内的高速目标。

在对拦截目标进行碰撞角约束时，最优化制导方法需要估计预测命中点的位置并计算剩余时间，从而给制导控制系统带来额外的负担，较大的剩余时间计算偏差会使最优制导退化为次优制导或者性能更差；而变结构控制方法则是直接在滑动超平面的表达式中考虑对视线角的约束，但是由于变结构控制方法的理论依据是Lyapunov稳定性原理，在制导律的推导过程中需要用到目标的运动和机动信息，而目标的机动加速度在现有条件下是难以获取的，因此只能对制导律的形式进行简化，这必然会影响制导律的性能。一般对于运动目标的碰撞角控制问题采用偏置比例导引的方法，但是现有的碰撞角约束制导方法均是针对一类典型目标(高速、低速或者静止目标)的单一拦截模式(顺轨或逆轨)进行设计，没有发现能够适用于多种模式拦截机动高速目标的碰撞角约束制导方法。

为了改变目前制导律的设计大多只能满足特定拦截模式(顺轨或逆轨)的典型目标(高速、低速或者静止目标)的拦截需求，本文将终端角度约束制导原理与全向自适应拦截导引理论[12]1118进行融合，设计具备碰撞角约束能力并能适应多种拦截模式的中段拦截制导律。该制导律不但能根据目标和拦截器的运动情况自行选择顺轨或逆轨拦截模式完成对目标的拦截制导，而且能够使拦截器按照预定的碰撞角与目标发生交会，满足弹道导弹中段防御对目标毁伤的要求。

1 碰撞角约束的目标与拦截器相对运动关系

二维平面内拦截弹与目标的相对运动关系如图1所示。

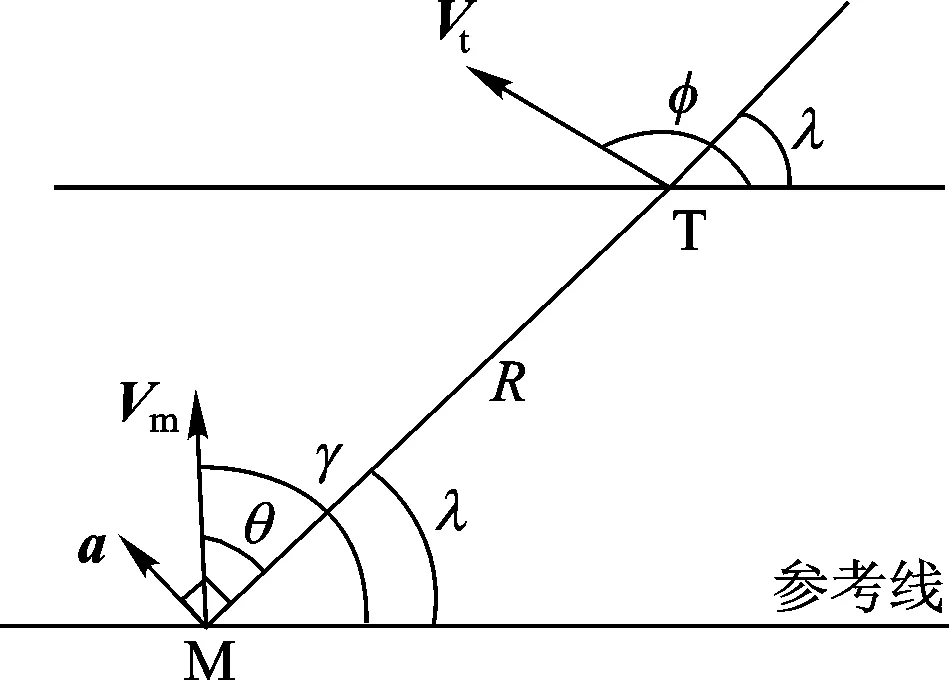
图1 平面内拦截弹与目标的相对运动

图1中，R为拦截弹到目标的距离，Vm为拦截弹速度，Vt为目标速度，φ为目标速度与参考线的夹角，λ为拦截弹与目标的视线(LineofSight，LOS)与参考线的夹角，γ为拦截弹路径倾角，Vm与视线的夹角定义为拦截弹速度前置角θ，a为拦截弹控制加速度，垂直于视线方向。拦截弹与目标之间的相对运动方程表述为

(1)

高速目标拦截制导律的研究表明，针对高速目标的拦截仅存在逆轨和顺轨2种拦截模式[12]1116。2种拦截模式下目标与拦截弹的交会几何关系，如图2所示。

a) 逆轨拦截模式

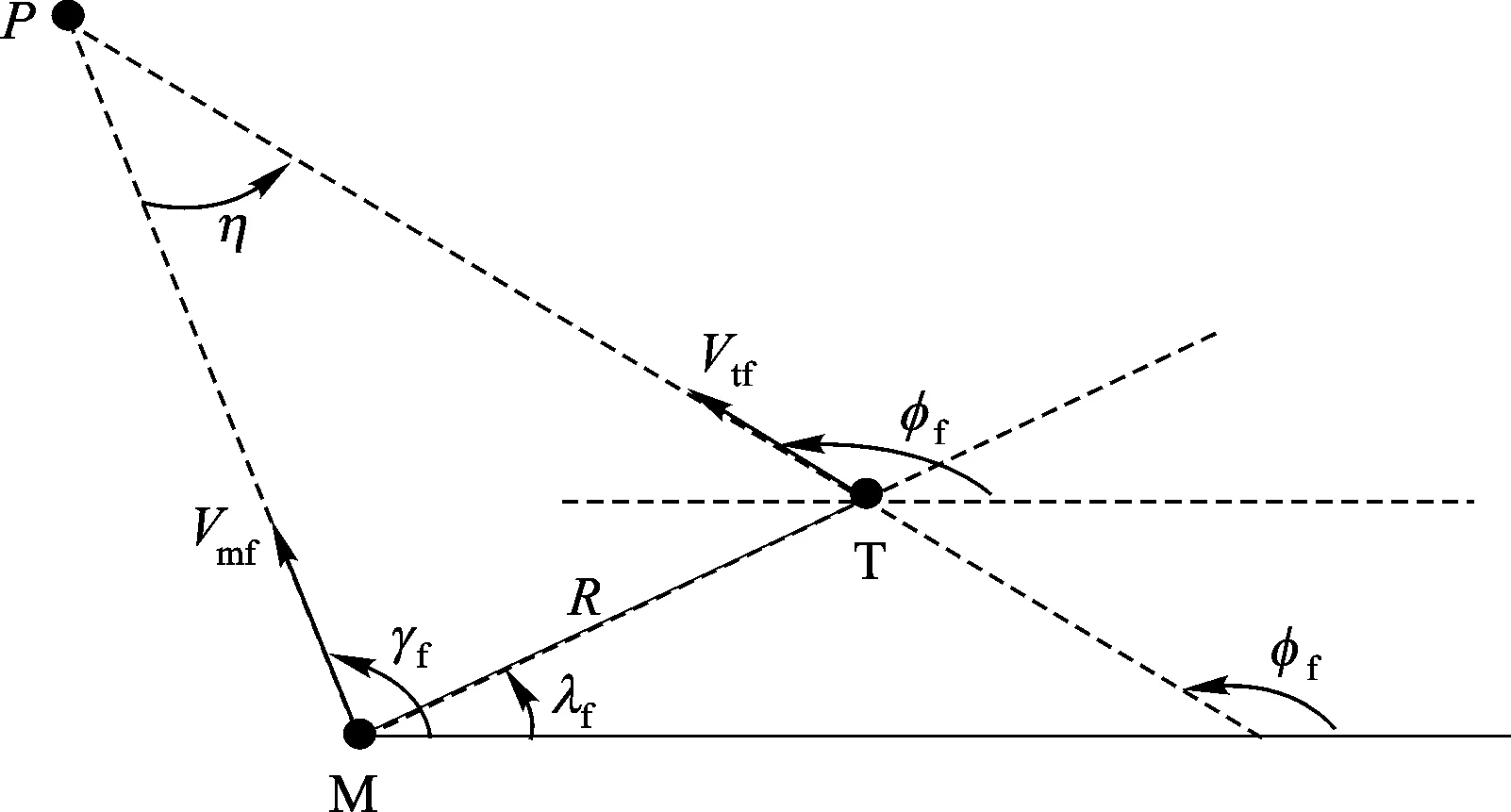
b) 顺轨拦截模式图2 拦截末端交会几何关系

图2中P为预定的碰撞点，M、T分别为碰撞前一时刻拦截弹与目标位置，Vtf、Vmf分为目标和拦截弹末速度，φf为目标末速度倾角，γf为拦截弹末速度倾角，λf为末视线角，η为碰撞角。由图2知

φf=γf+η

(2)

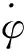
(3)

式中，tgo为剩余拦截时间。比例导引中速度角速率与视线角速率关系

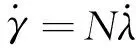
(4)

式中，N为比例系数。将式(4)代入制导的初始和末端条件，则拦截弹在碰撞时刻视线角λf为

(5)

对于目标机动角速率恒定的情况有

(6)

(7)

以目标为观察点，将拦截弹与目标的相对运动速度Vc在沿视线坐标系进行分解，如图3所示。

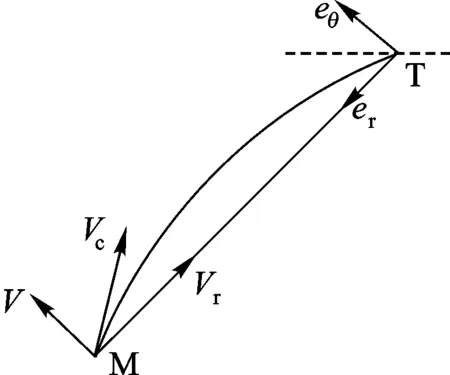
图3 相对速度分解示意图

Vtfsin(φf-λf)=Vmfsin(γf-λf)

(8)

定义碰撞时刻的目标与拦截弹速度比

βf=Vtf/Vmf

(9)

将式(2)代入式(8)化简后有

(10)

由式(10)知，对于恒速非机动的拦截目标约束碰撞角的情况：(1) 在末端视线角一定的情况下，存在着一系列满足式(10)条件的末端速度前置角和速度比的取值，任一组取值均可满足预定的碰撞角约束要求；(2) 末端目弹速度比的不同对应着不同的末端速度前置角的取值，因此变速拦截制导律相对于恒速拦截制导律在碰撞角控制方面具有更大的灵活性和可选择性。

2 碰撞角约束的全向真比例制导方程

2.1 全向拦截的偏置比例导引方程

文献[12]1120推导了全向拦截制导律，通过将拦截弹的速度前置角引入制导律计算，实现全平面内的自适应顺/逆轨全向拦截,如图4所示。本文基于全向拦截导引进一步研究适用于全向拦截制导并具备碰撞角控制能力的新型拦截制导律。

图4 平面内全向拦截示意图

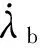
(11)

将式(1)中第二式两边微分并代入式(11)，有

(12)

整理并代入式(1)中第一式，得

(13)

将拦截弹和目标的加速度在视线坐标系分解，如图5所示，图中at为任意方向的目标加速度，at与参考线的夹角为χ。

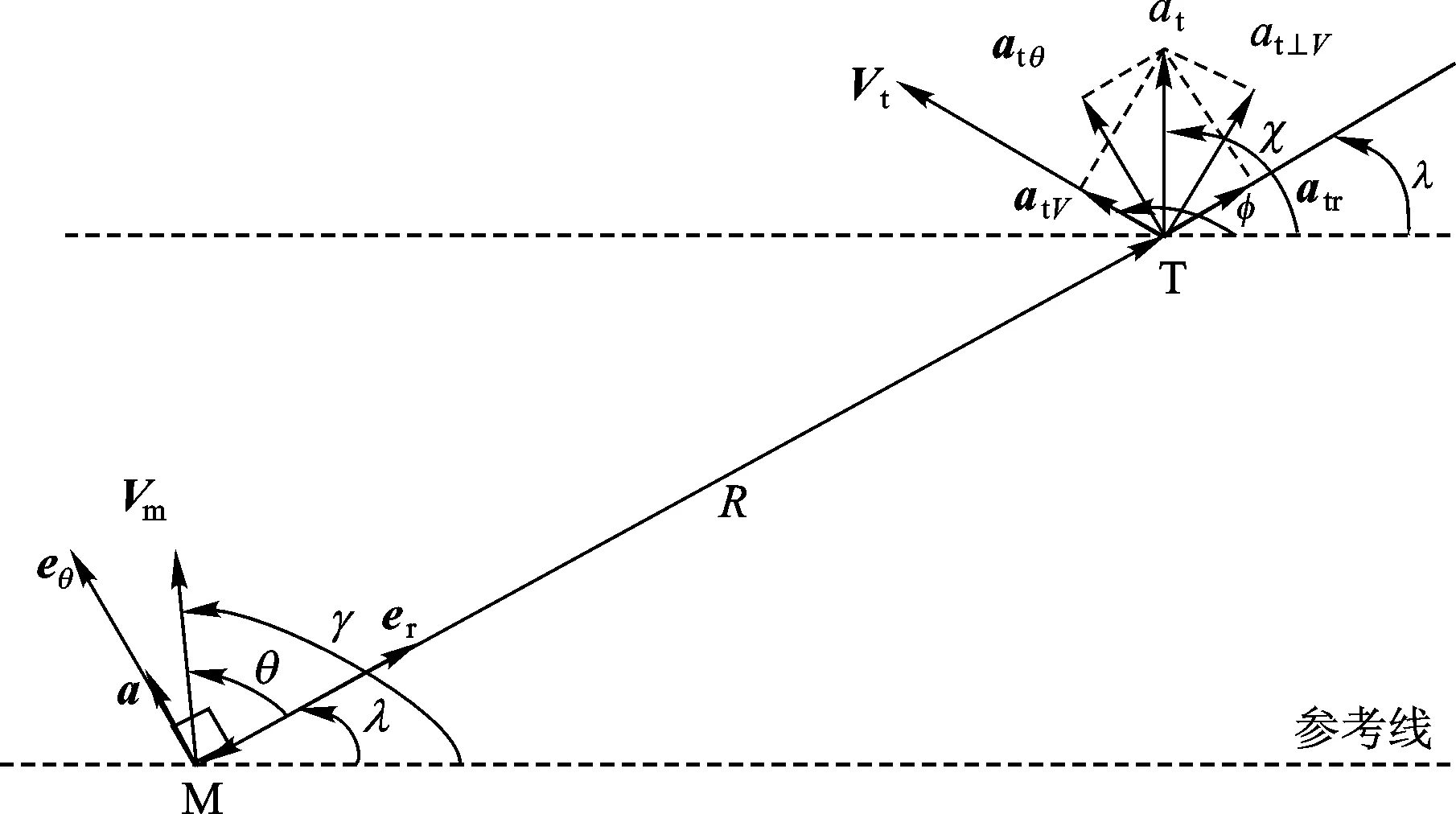
图5 视线坐标系下加速度分解示意图

由于拦截弹的控制力垂直视线，有

(14)

将式(14)第一式代入式(13)得

(15)

(16)

因此,拦截弹的控制加速度

(17)

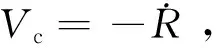
(18)

由式(18)可知有效导航比N′在导航比N取为常数的情况下受到速度前置角、拦截弹速度以及弹目相对速度的影响。式(17)可改写为

(19)

2.2 时变偏置角速率求解

对于拦截弹在比例导引下拦截非机动目标的情况，由式(14)第二式，代入atθ=0，amθ=a，得

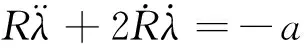
(20)

将式(11)代入式(20)整理后得微分方程

(21)

由于

(22)

tf为拦截达成时刻，将式(22)代入式(21)有

(23)

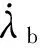
(24)

碰撞时刻tf的末端视线角λf为

(25)

由于末端视线角λf为已知，解得此时所需的偏置角速率为

(26)

采用式(17)、式(18)和式(26)作为制导方程，可得到具备碰撞角约束功能的高速目标拦截导引律。由于式(17)具备自适应全向拦截的功能，因此该制导律只要分别设定满足要求的顺轨和逆轨碰撞角约束条件，即可实现在平面内的具备角控功能的全向拦截制导，将该制导律记为碰撞角约束的全向真比例(AC-OTPN)制导律。

由本节分析可知，拦截器速度前置角余弦值cosθ的符号不同时，需要针对顺轨、逆轨拦截模式分别设定不同的末端期望碰撞角，在拦截制导中期望碰撞角的装订依据为

(27)

3 AC-OTPN制导律拦截制导数值仿真和分析

3.1 逆轨拦截模式下的AC-OTPN制导律仿真

为验证本文提出的制导律制导和碰撞角控制效果，使用MATLAB进行拦截仿真，仿真中设定有效拦截为最终脱靶量小于10m、碰撞角误差小于0.5°，拦截弹在距离目标30m内失盲后制导指令保持为最终数值。为了验证AC-OTPN制导律对高速目标实施逆轨拦截中的碰撞角约束能力，将目标速度设定为拦截弹初始速度的2.5倍，拦截弹初始速度倾角的范围设置从-60°变化至60°，变化步长设置为6°。其他仿真参数设置如表1所示，制导控制力不设约束上限。仿真结果如图6～图9所示。

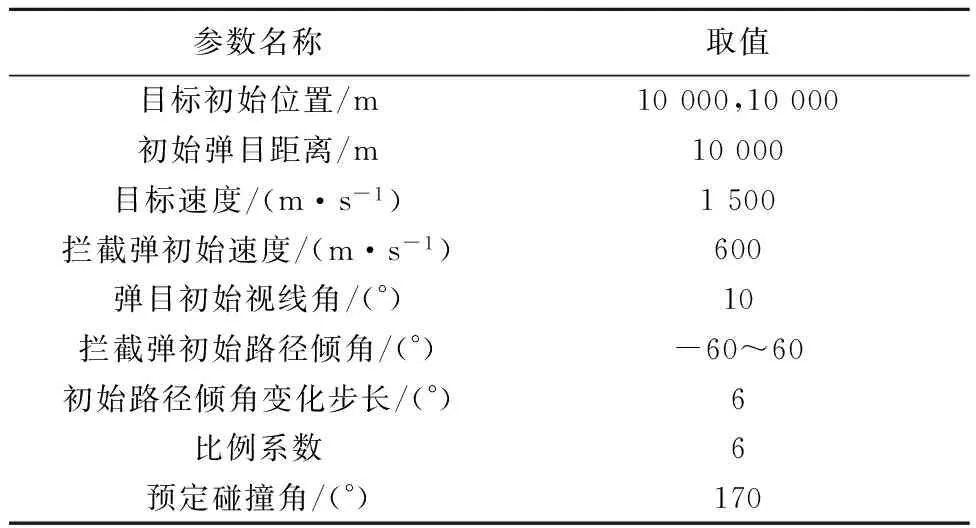
表1 逆轨拦截仿真参数

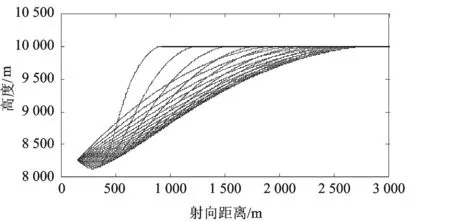
图6 拦截弹与目标飞行轨迹

图7 拦截弹指令加速度变化

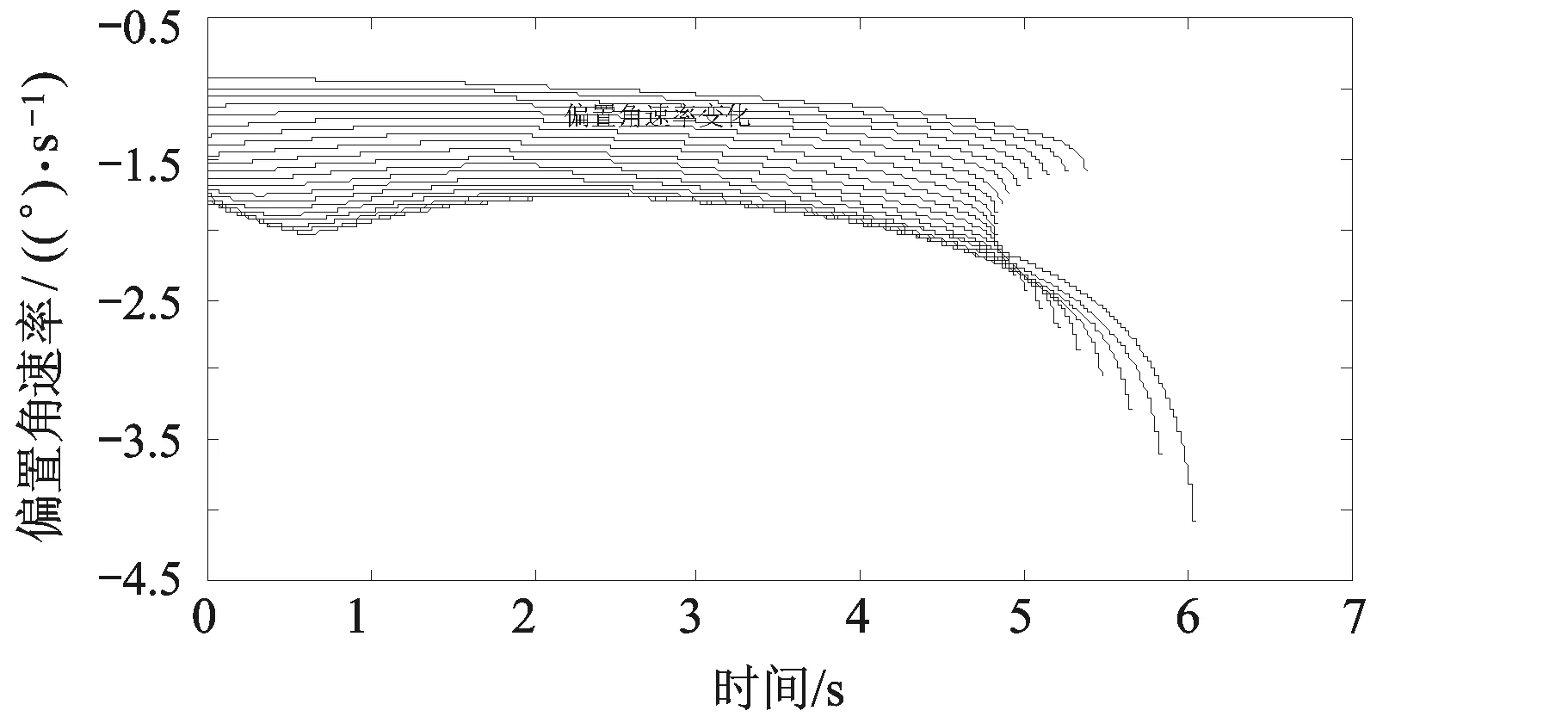
图8 拦截过程中的偏置角变化率

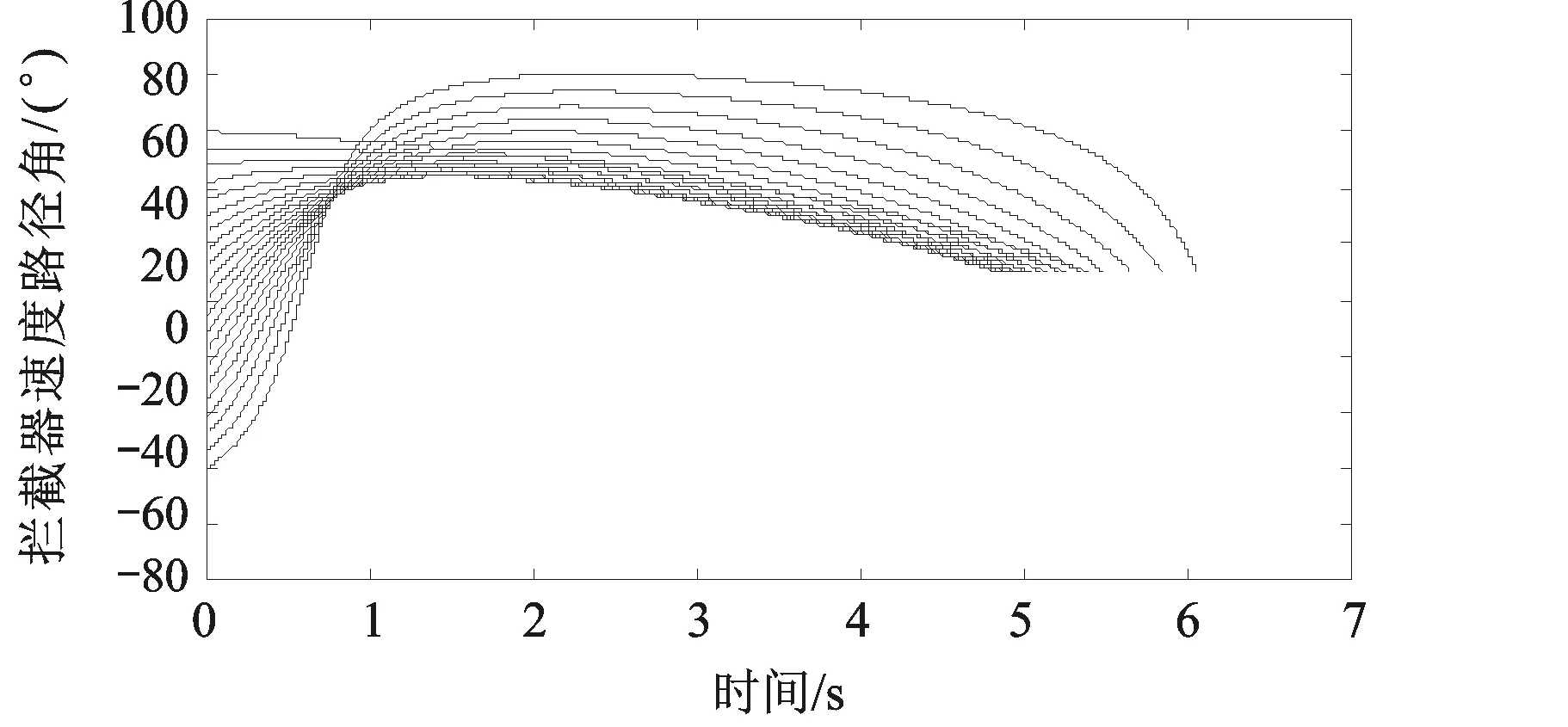
图9 拦截弹路径倾角变化

仿真结果表明：

1) 由图6可知，AC-OTPN制导律可有效对高速目标进行逆轨拦截制导，碰撞角精度和最终脱靶量均满足成功拦截需求；由图8可知，通过增加时变偏置角速率调整拦截器的速度倾角，在制导过程可实现对最终碰撞角的有效控制，使得不同初始条件的拦截器都能够以预定的碰撞角拦截目标；

2) 由图7知，AC-OTPN对高速目标进行碰撞角约束的逆轨拦截导引中，所需的最大控制力与拦截的初始状态有关，初始速度前置角越大，导引所需的最大控制力和总控制量需求越大，在实际应用中可以设置最大控制力阈值来减小制导律在起始阶段的需用过载；

3) 由图9可知，AC-OTPN制导律在制导过程可实现对最终碰撞角的有效控制，使得不同初始条件的拦截弹都能够以预定的碰撞角拦截目标；

4) 由图8可以看出，在制导过程中AC-OTPN制导律使用的偏置角速率变化平稳，具体取值与初始制导条件有关，初始偏差角越大，制导中所需的偏置角速率越大，在制导过程中偏置角速率随时间发生变化；

5)对图8进行分析可知，由于在制导指令中增加了时变偏置角速率，在制导过程中当拦截弹与目标处于平行接近状态时，偏置角速率的存在会使得拦截弹在控制加速度作用下发生偏离，因此制导末端的视线角速率不为零。

3.2 顺轨拦截模式下AC-OTPN制导律仿真

基本参数设置如表1所示，预定碰撞角设为10°，拦截弹初始路径倾角范围取为100°～260°，仿真结果如图10～图13所示。

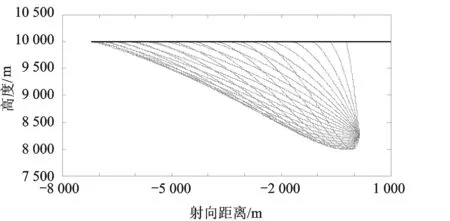
图10 拦截弹与目标飞行轨迹

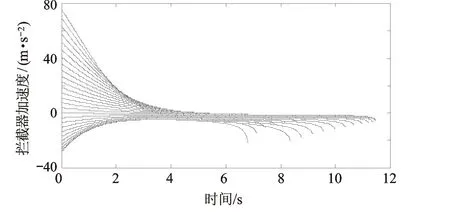
图11 拦截弹指令加速度变化

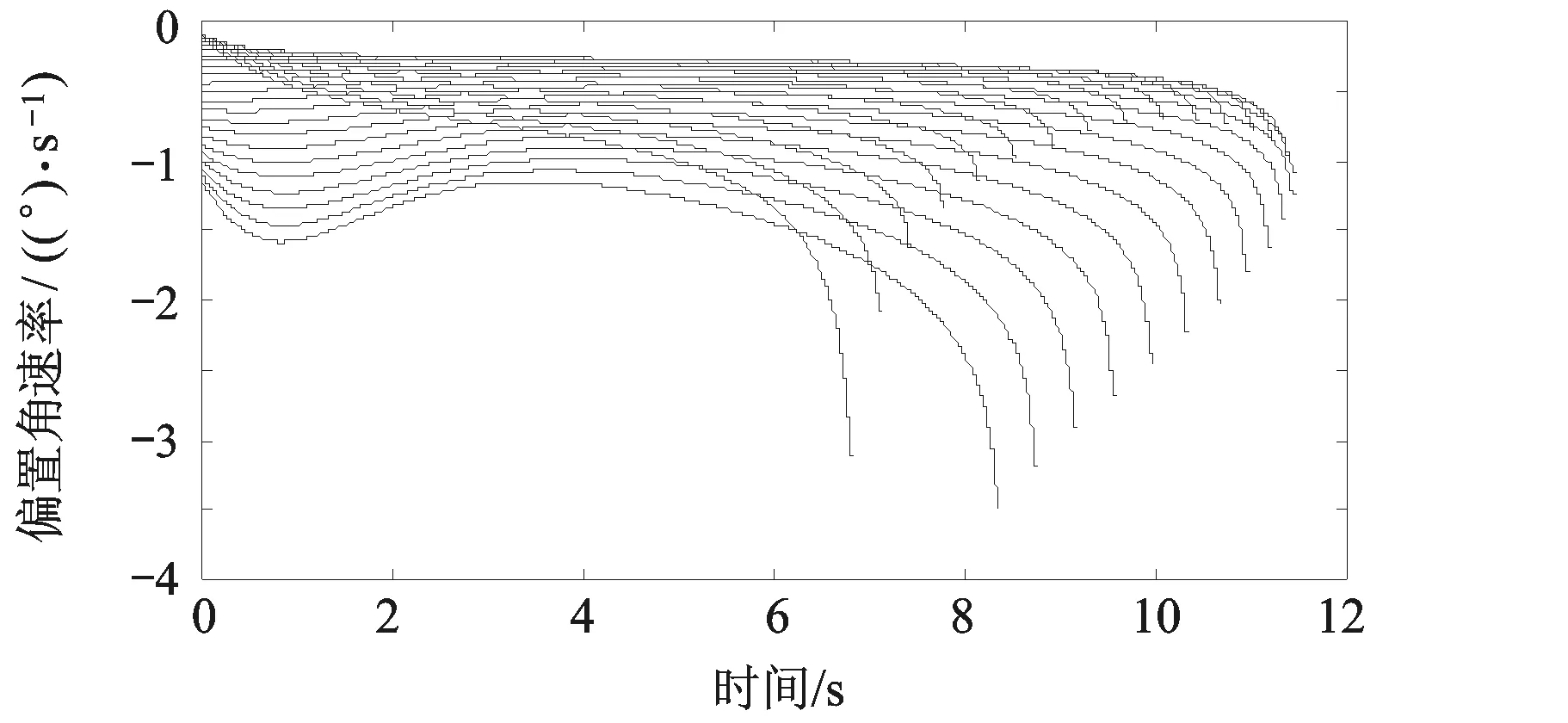
图12 拦截过程中的偏置角变化率

图13 拦截弹路径倾角变化

仿真结果表明：

1) 由图10可知，AC-OTPN制导律可以对高速目标进行带碰撞角约束的顺轨拦截制导，碰撞角控制精度和最终脱靶量能满足拦截制导需求；由图12知在制导过程中，AC-OTPN制导律使用的偏置角速率变化平稳，具体取值同样与初始制导条件有关；

2) 对比图7和图11可以看出，顺轨拦截时拦截弹所需的最大加速度远小于逆轨拦截，同等条件下顺轨拦截时间长于逆轨拦截，弹目相对速度较小，因此对于制导所需最大控制力的要求更小；

3) 由图13可知，AC-OTPN制导律在制导过程中可实现对最终碰撞角的有效控制，使得不同初始条件的拦截弹都以预定的碰撞角拦截目标。

3.3AC-OTPN自适应全向拦截性能验证

为了进一步研究AC-OTPN制导律在全平面内对高速目标的自适应拦截导引及碰撞角的控制能力，将拦截弹初始路径倾角范围设定为0～360°来考察该制导律的拦截制导性能。仿真基本参数设置如表2所示，设定顺轨拦截下预定碰撞角为20°，逆轨拦截模式下预定碰撞角为160°，初始路径角变化步长为5°，成功拦截条件为末端脱靶量小于10m，末端碰撞角误差小于0.5°，为便于观察和分析AC-OTPN制导律的末端碰撞角控制能力，对制导控制力不设约束上限。

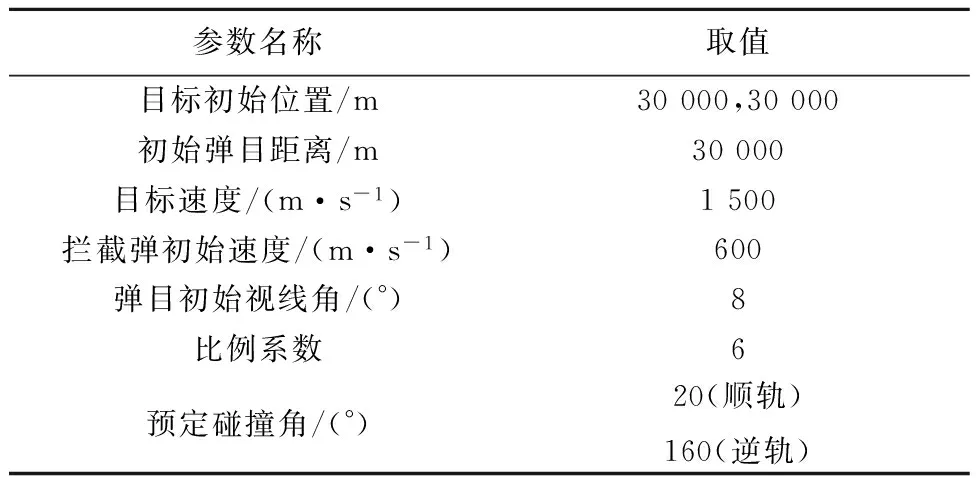
表2 全向拦截仿真参数

AC-OTPN制导律对高速目标的全向拦截仿真结果如图14和图15所示。由图14可知，在不限控制加速度上限的情况下，AC-OTPN可根据拦截弹的初始参数自动选择顺轨或逆轨拦截模式，导引平面内任意初始路径倾角的拦截弹成功拦截目标并满足该模式下预定的碰撞角要求。

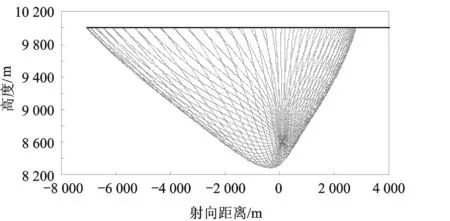
图14 AC-OTPN全向自适应拦截轨迹

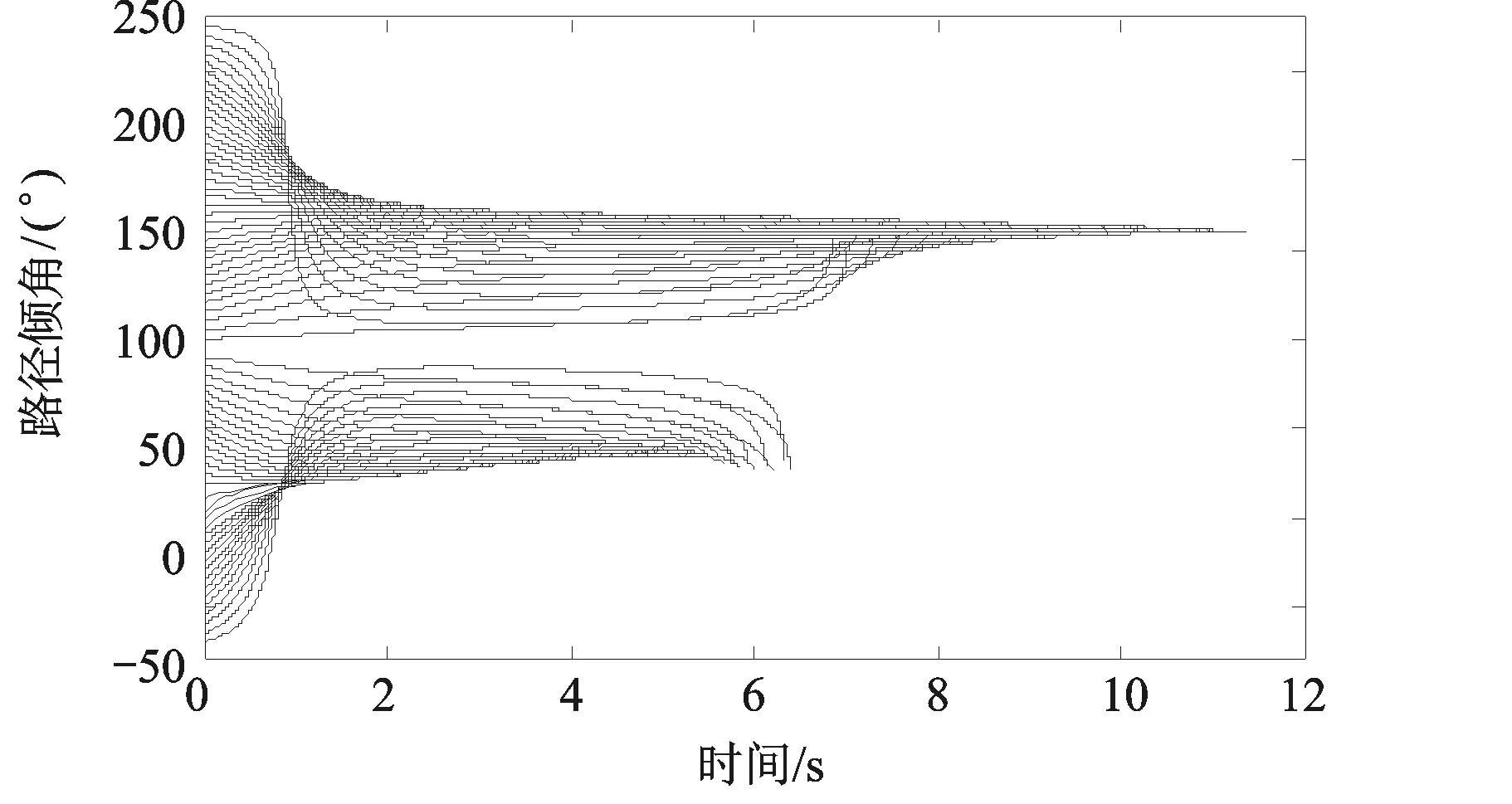
图15 拦截弹路径倾角变化

图15显示出不同初始条件的拦截弹在AC-OTPN的导引下，自动选择拦截模式并向对应的预定拦截路径角进行调整的过程，从图中能清晰地看到制导过程中拦截弹路径倾角的变化趋势。

4 结 束 语

理论推导和数值仿真的结果表明：本文提出的AC-OTPN制导律能够按照给定的末端碰撞角约束条件，在满足拦截器对目标的末端碰撞角度要求的同时，自适应完成顺、逆轨拦截制导；对拦截制导的数值仿真结果分析可看出，在自适应拦截制导律中增加末端碰撞角约束后制导所需的最大控制力与拦截时间成反比，在拦截器的控制力存在限制的情况下，顺轨拦截比逆轨拦截增加碰撞角控制所花费的控制代价更小。AC-OTPN制导律可通过调整理想的末端碰撞角以增强拦截碰撞效能，使得相对质量、体积较小的拦截器同样具备较强的毁伤能力，为拦截器的小型化设计和携带更多的子拦截器提供技术支撑。

)

[1]SIOURIS G M.Missile guidance and control systems[M].New York：Springer,2004：142-173.

[2]YANUSHEVSKY R.Modern missile guidance[M].Boca Raton，FL：CRC Press,2007：12-18.

[3]KIM B S,LEE J G,HAN H S.Biased PNG law for impact with angular constraint[J].IEEE Transactions on Aerospace and Electronic Systems,1998,34(1):277-288.

[4]RATNOO A,GHOSE D.Impact angle constrained guidance against non-stationary no maneuvering targets[J].Journal of Guidance,Control,and Dynamics,2010,33(1):269-275.

[5]RATNOO A,HAYOUN S Y,GRANOT A,et al.Path following using trajectory shaping guidance [J].Journal of Guidance,Control,and Dynamics.2015,38(1):106-116.

[6]ERER K S， MERTTOPCUOGLU O.Indirect impact-angle-control against stationary targets using biased pure proportional navigation[J].Journal of Guidance,Control,and Dynamics,2012，35(2):700-704.

[7]ZARCHAN P.Tactical and strategic missile guidance[M].3rd ed.Reston:AIAA,2002:15.

[8]SHIMA T,GOLAN O M.Head pursuit guidance[J].Journal of Guidance,Control,and Dynamics,2007,30(5):1437-1444.

[9]SHIMA T.Intercept-angle guidance[J].Journal of Guidance,Control,and Dynamics，2011,34(2):484-492.

[10]胡锡精,黄雪梅.具有碰撞角约束的三维圆轨迹制导律[J].航空学报,2012,33(3):508-519.

[11]闫梁，赵继广，沈怀荣，等.带末端碰撞角约束的三维联合偏置比例制导律设计[J].航空学报，2014,35(7):1999-2010.

[12]白国玉，沈怀荣，闫梁，等.拦截高速目标的全向真比例制导律研究[J].北京航空航天大学学报,2016(6):1116-1125.

(编辑：李江涛)

Research on Omnidirectional Interception Guidance Law
with Impact Angle Constraint

BAI Guoyu1, SHEN Huairong2, YAN Liang3, LI Yuan3

(1. Department of Graduate Management, Equipment Academy, Beijing 101416, China； 2. Department of Space Equipment, Equipment Academy, Beijing 101416, China； 3. Beijing Institute of Tracking and Telecommunications Technology, Beijing 100094, China)

To address the problem of impact angle constraint in the design of space interception guidance law, the paper puts forward the impact Angle-Constraint Omnidirectional True-Proportional Navigation (AC-OTPN) guidance law and solves the technical problem of high-speed target interception with terminal impact angle constraint. Based on OTPN, AC-OTPN is added with time-varying bias angle velocity. It also real-timely solves time-varying bias angle rate, hoping to get expected terminal impact angle. AC-OTPN can self-adaptively choose head-on and head-pursuit interception patterns according to the motion relationship of target and interceptor. It has large capture region and high accuracy of impact angle. By adjusting the terminal impact angle, AC-OTPN can increase the impact effectiveness. Interceptors with less mass and smaller volume can also have the same kill ability. AC-OTPN provides technical support for the miniaturization design of interceptors and their ability to carry more sub-interceptors.

impact angle; constraint; omnidirectional; interception; guidance law

2017-03-23

部委级资助项目

白国玉(1974—)，男，高级工程师，博士研究生，主要研究方向为航天任务分析与总体。744491373@qq.com 沈怀荣，男，教授，博士生导师。

V448.133

2095-3828(2017)03-0092-07

A DOI 10.3783/j.issn.2095-3828.2017.03.016