液体推进剂爆炸冲击波数值计算及实验误差分析

王 岩， 王 华， 崔村燕， 赵蓓蕾， 辛腾达

(1. 装备学院 研究生管理大队, 北京 101416； 2. 装备学院 航天装备系, 北京 101416)

液体推进剂爆炸冲击波数值计算及实验误差分析

王 岩1， 王 华2， 崔村燕2， 赵蓓蕾1， 辛腾达1

(1. 装备学院 研究生管理大队, 北京 101416； 2. 装备学院 航天装备系, 北京 101416)

液体推进剂爆炸危害后果的精确计算需要对爆炸当量进行精确估算，实验测量存在高成本、高风险的缺点，而数值计算成本低、时间快、可重复性强，因而成为爆炸冲击波危害性研究的一种重要手段。基于爆炸相似律，利用LS-DYNA有限元软件对开放空间N2O4/UDMH爆炸模型进行了数值计算，研究了液体推进剂爆炸冲击波在无限空气域的传播规律。通过仿真值和实验值的对比分析，将引起实验误差的主要原因总结为测量点布置高度、测量装置加固情况和推进剂混合不均匀，并给出了相应的建议。

爆炸冲击波；数值计算；传播规律；实验方案

偏二甲肼(UDMH)和四氧化二氮(N2O4)是当前我国长征系列运载火箭广泛使用的液体推进剂组合，使用过程中的安全问题一直倍受关注。液体火箭一旦发生意外爆炸，将会造成巨大的经济损失，甚至重大人员伤亡。为了将液体推进剂意外爆炸产生的冲击波对发射场人员和设施设备的危害控制在最小范围，保护地面人员安全和设施设备不受损害，国内外许多单位和学者针对爆炸冲击波的危害特性展开了大量研究。

20世纪60—80年代期间，美国ADL公司的PYRO项目对液氢/液氧推进剂在不同混合模式下的爆炸特性进行了实验研究，提出了计算冲击波超压的数学模型[1]；美国的海陆空三军、NASA[2]、圣安东尼奥西南研究院[3]等单位对液体推进剂、民用燃料爆炸危害性进行了理论和实验研究。就国内而言，自20世纪90年代开始，国内许多学者就爆炸冲击波开展了大量的实验和仿真研究：陈新华等[4-5]开展了十余次不同当量的液体推进剂爆炸实验研究，改进了冲击波危害性评估方法；郑治仁[6]确定了某型号火箭地面爆炸安全距离，并给出了危险区划分方法；仲倩等[7]采用实验方法测定了TNT冲击波超压并拟合出了改良的经验公式；孙克等[8]对低温液体推进剂危害性问题进行了研究，提出了利用事故后果建立爆炸事故模型的方法；杨亚东等[9]针对传统经验公式存在的不足，采用仿真和文献数据结合的方法，对冲击波超压等参数进行了预测；吴彦捷等[10]综述了21种常用冲击波超压预测经验公式，并采用加权平均方法对经验公式进行了修正；段晓瑜等[11]对TNT等3种炸药进行了实验研究，并进行了幂指数公式拟合，结果表明幂指数公式在取对数后的经验公式准确性更好。

从国内外研究进展可以看出：国外对冲击波传播规律的研究较早，通过大量实验提出了数学计算模型；国内目前多是针对特定工况下进行的研究，在实验的规模及次数上与国外相比具有一定差距，且得出的定性结论较多。因此，为了更好地研究N2O4/UDMH推进剂在开放空间爆炸冲击波传播规律，优化改进爆炸实验方案，本文对开放空间N2O4/UDMH液体推进剂的爆炸进行了数值计算及实验对比研究。

1 爆炸相关理论

液体火箭爆炸后，破坏作用主要包括冲击波、火球、热辐射、碎片和有毒气体，其中占总爆炸能量70%～85%的冲击波是最主要破坏。根据空气冲击波传播规律相关理论可知：爆炸能量越大，冲击波超压越强，传播距离越远，冲击波超压随着距离的增加呈指数衰减趋势[12]。

1.1 爆炸当量的确定

根据爆炸相似律，选用TNT模型，将液体推进剂质量换算成等效TNT当量，利用TNT炸药的爆炸规律预测液体推进剂的爆炸规律[13]，换算公式如下：

WT=Y·W0

(1)

式中:WT表示等效TNT的质量；Y表示爆炸当量系数；W0表示N2O4和UDMH的总质量[14]。

1.2 冲击波超压理论公式

空气冲击波参数中的峰值超压ΔP，是指冲击波波阵面上峰值压力减去空气中的原始压力(一般是标准大气压)，是衡量冲击波破坏作用的重要指标[15-16]。文献[17]44给出了冲击波峰值超压的计算公式[见式(2)和式(3)]，其中ΔP的单位为MPa。该公式适用于地面发生的爆炸在无限空气域中的传播情况，因此本文采用该公式进行理论计算。

(2)

(3)

式中，R为距离爆心的距离。

2 爆炸冲击波数值计算与分析

根据文献[4]34-35中陈新华教授所做的实验，利用LS-DYNA有限元软件，对爆炸模型进行数值计算和分析。

2.1 有限元模型和计算方法

LS-DYNA软件支持Lagrange、Euler和ALE 3种算法，ALE算法兼有Lagrange和Euler两者的优点，在处理固体极大变形问题上有较大优势，因此，本文采用ALE算法对TNT和空气具有流体性质的材料模型进行计算。仿真模拟的是液体推进剂地面爆炸形成冲击波在空气中传播的情况，数值模拟采用的基本材料为TNT炸药和空气，单元类型选取三维SOLID 164八节点单元，单位制采用cm-g-μs。空气采用MAT_NULL材料模型和线性多项式状态方程EOS_LNIEAR_ POLYNOMIAL进行描述。空气域的边界处采用无反射边界条件，允许空气的流出，使有限元模型能够更好地模拟空气介质的无限边界,对称面施加零位移约束，为了简化计算模型，将数值模拟中的地面视为刚体，忽略由爆炸冲击波所引起的变形。炸药柱的起爆方式采用点起爆。

为与文献[4]38中的实验结果进行比对，推进剂总重量分别取100 kg、300 kg和500 kg，UDMH质量和N2O4质量分别用W1和W2表示。根据美国军用爆炸物安全委员会对液体推进剂爆炸TNT当量系数上限所做的规定，分别选取当量系数的下限0.05和上限0.1进行仿真计算，分别得到仿真结果的下限值和上限值。仿真分为6组，各组选定炸药柱半径r为10 cm、空气域半径R为1 100 cm，炸药柱高为h，空气域高为H，如表1所示。

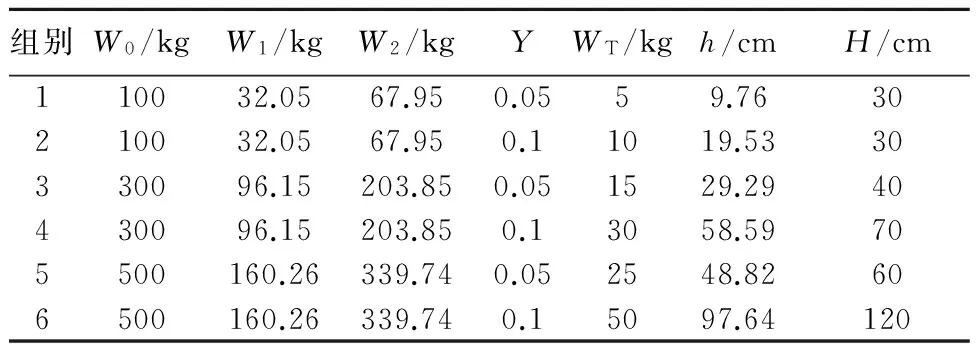
表1 模型参数表

2.2 仿真结果分析

对计算结果进行后处理，选取了冲击波传播过程中的4个时刻，反映了药柱爆炸后冲击波超压在空气中的传播过程，详见图1a)～图1d)，色带中超压值的单位为105MPa。

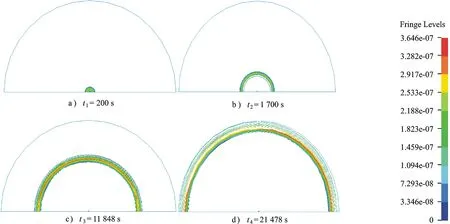
图1 爆炸后不同时刻冲击波在空气中的传播过程

图1a)所示是炸药柱起爆后，冲击波在空气中传播初期阶段；图1b)、图1c)所示，冲击波继续在空气中传播，冲击波中心的压力波高于两边，超压峰值随着距离的增加而减小；图1d)所示，可以明显观察到冲击波波阵面面积随传播距离的增加而不断增大，并且距离爆心等半径圆上的冲击波颜色基本相同，说明距爆心等距离处的超压值大小基本相等。

将6组仿真中5 m、8 m和10 m不同测点的超压时程曲线绘制在图2中，将每组仿真中3个不同测点处的超压峰值记入表2中，得到冲击波超压仿真结果。

从图2可以看出，在推进剂质量相同的情况下，距爆心距离相同位置，不同当量系数下的超压值一般不同，且当量系数越大超压值越大；在当量系数相同，距爆心距离相同的情况下，炸药当量越大，超压值越大；在推进剂质量和当量系数均相同的情况下，冲击波超压值随爆心距离R的增加而减小，且距爆心距离越远冲击波宽度越大，说明传播速度随着爆心距离的增加而减小。

表2 仿真结果与经验值及相对误差

图2 不同质量推进剂的不同测点超压时程曲线

3 结果对比分析

3.1 仿真结果与经验值对比分析

运用经验公式(2)和(3)对表1中所列6组超压值进行计算，得到冲击波超压值，然后计算仿真结果与经验值之间的相对误差，如表2所示。

将表2中相对误差绘成图3所示柱状图，可以清晰地看出，仿真结果与经验值的相对误差不超过29%，仿真结果与经验值基本吻合，误差在可接受范围内，验证了模型的准确性。

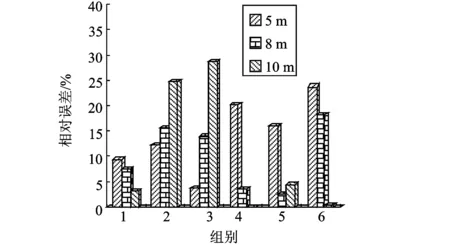
图3 仿真结果与经验值的相对误差

通过以上数据分析可知，仿真结果与经验值存在一定的误差，原因主要有3个方面：(1) 开放空间爆炸是指炸药在无边界的空气中爆炸，而经验公式是根据大量实验结果总结出来的。实验中的爆炸冲击波传播会受到地面的影响，不是向整个空气域传播，而仿真中没有考虑地面的影响，导致仿真结果与经验公式存在一定误差。(2) 由于当量系数是根据不同爆炸模式，参考国外总结的液体推进剂当量系数选择范围选取的，选择范围较为宽泛，导致误差较大，对仿真结果产生一定的影响。(3) 根据文献[17]44中的研究结论可知，模型的网格密度也会对计算精度造成一定的误差。

3.2 仿真结果与实验值对比分析

为了研究N2O4/UDMH液体推进剂爆炸冲击波的特性，文献[4]38对不同当量液体推进剂开展了爆炸实验。实验中通过对5 m、8 m、10 m处的冲击波超压进行测定，得到了3个不同测点处的冲击波超压实验值，如表3所示。

通过对表3中的数据分析可知：文献[4]38所得的部分实验值只有一组与仿真结果较吻合，即500 kg、10 m处实验值0.800，其余数据与仿真结果均存在一定误差。有些误差较小，为8.95%，有些误差较大，超过了200%，有些误差值甚至接近400%。

限于当时实验条件，实验结果难免存在一定误差。为了客观分析实验中存在的问题，为今后实验方案的设计提供一定的参考，通过对实验过程的深入分析，将产生误差的可能原因归结为：

1) 测量点布置的高度所导致的误差。由于距爆心某一距离处，冲击波超压纵向分布并不等值，实验条件下测量点布置的高度与仿真中拾取点的高度并非完全吻合，导致实验值与仿真结果存在一定误差。

2) 测量装置的加固情况所导致的误差。由于压电传感器置于固定在地面的直杆上，若直杆固定不稳，在爆炸产生的震动作用下，会使直杆倾倒，从而导致传感器测量数据与预定测量位置不相符，造成测量结果不准确。

3) 推进剂混合不均匀所导致的误差。爆炸装置推进剂混合形式不具有可控性，不均匀的混合方式致使爆炸冲击波的传播方向不是均匀的球面型，造成了实验结果与仿真值的误差。

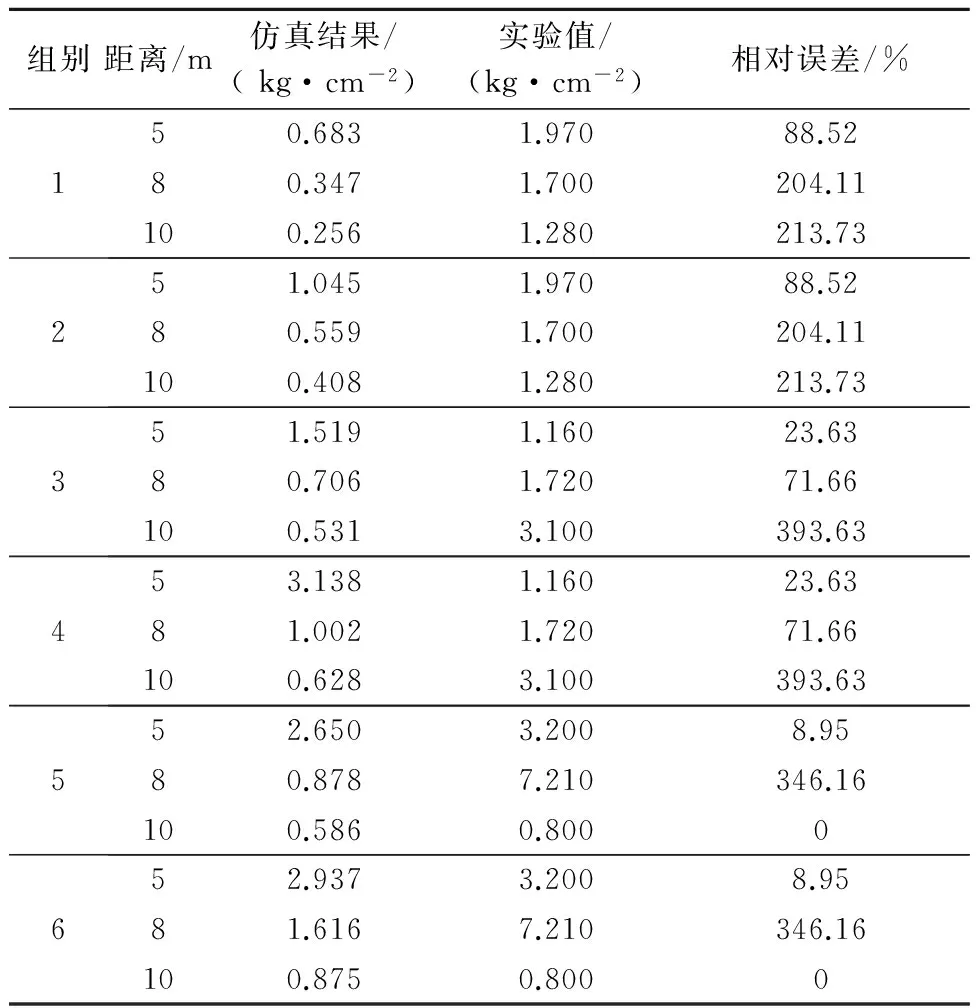
表3 仿真结果与实验值及相对误差

4 结 束 语

本文针对爆炸实验中存在的问题，通过建立开放空间N2O4/UDMH有限元模型，对液体推进剂爆炸冲击波的传播规律进行了数值仿真，将仿真结果与实验值进行了对比分析，总结出实验中产生误差的原因。今后开展液体推进剂爆炸实验时，建议重点从优化测量点高度的布置、对测量装置进行良好加固、设置足够多测点等方面，对实验方案进行优化改进，从而提高液体推进剂爆炸冲击波实验的准确性和可信性。

References)

[1]WILLOUGHBY A B,WILTON C,ANSFIELD J.Liquid propellant explosive hazards:Volue 3[R].California:URS Research Copany,1969:10-136.

[2]BAKER W E,KUIESZ J J,RICKER R E.Workbook for predicting pressure wave and fragent effects of exploding propellant tanks and gas storage vessels[R].Washington D.C.:NASA,1995.

[3]贝克W E,威斯汀P S,考克斯P A.爆炸危险性及其评估[M].张国顺，译.北京:群众出版社，1988：11-135.

[4]陈新华,张智,王振国，等.液体推进剂爆炸理论与试验研究[J].爆炸与冲击,1996,16(1):31-40.

[5]CHEN X H,NIE W S.Research of explosive characteristic of hypergolic propellant[C]//International Autun Seinar on Propellants,Explosives and Pyrotecnics.Beijing:Journal of Safety and Environent,2003:300-304.

[6]郑治仁.运载火箭的爆炸与发射场的安全距离[J].航天发射技术,2000(1):34-39.

[7]仲倩,王伯良,黄菊，等.TNT空中爆炸超压的相似率[J].火炸药学报,2010(4):32-35.

[8]孙克,陈景鹏,赵继广，等.低温液体火箭塔台爆炸事故危害性分析[J].计算机仿真,2013(3):109-113.

[9]杨亚东,李向东,王晓鸣.爆炸冲击波空中传播特征参量的优化拟合[J].爆破器材,2014(1):13-18.

[10]吴彦捷,高轩能.爆炸冲击波数值模拟及超压计算公式的修正[J].华侨大学学报(自然科学版),2014(3):321-326.

[11]段晓瑜,崔庆忠,郭学永，等.炸药在空气中爆炸冲击波的地面反射超压实验研究[J].兵工学报,2016(12):2277-2283.

[12]李翼祺,马素贞.爆炸力学[M].北京:科学出版社,1992:237-318.

[13]杨鑫,石少卿,程鹏飞.空气中TNT爆炸冲击波超压峰值的预测及数值模拟[J].爆破,2008,25(1):15-16.

[14]彭明伟,陈新华.液体推进剂爆炸实验冲击波超压分析[J].指挥技术学院学报,2001,12(4):58-61.

[15]陈新华,聂万胜.液体推进剂爆炸危害性评估方法及应用[M].北京：国防工业出版社,2005:126.

[16]蒋浩征.爆炸及其作用[M].北京：国防工业出版社,1979:259-263.

[17]张广福,刘玉存,王建华.爆炸冲击波无限空气领域传播的数值模拟研究[J].山西化工,2009,29(1):44-46

(编辑：李江涛)

Study on Numerical Calculation of Liquid Propellant Blast Shock Wave and Experiment Error Analysis

WANG Yan1， WANG Hua2， CUI Cunyan2， ZHAO Beilei1， XIN Tengda1

(1. Department of Graduate Management, Equipment Academy, Beijing 101416, China； 2. Department of Space Equipment, Equipment Academy, Beijing 101416, China)

The accurate calculation of the explosion equivalent needs to be used in the accurate calculation of the damage consequence of liquid propellant blast. The experimental measurement has the disadvantages of high cost and high risk. Numerical calculation is an important method to study the harmfulness of blast wave, because of its low cost, rapidity and strong repeatability. According to the Blasting Similarity Theory, LS-DYNA is used to calculate the open space N204/UDMH blast model. The propagation law of the blast wave of liquid propellant in the open air is studied. Through the comparative analysis between simulation results and experiment results, the causes of the experimental errors are summarized as the height of the measuring point, the reinforcement of the measuring device and the inhomogeneous mixing of the propellant, with some suggestions given to provide reference for the improvement of the experiment accuracy.

blast shock wave; numerical calculation; propagation law; experimental program

2017-03-14

王 岩(1989—)，男，博士研究生，主要研究方向为飞行器测试与控制。770743312@qq.com 王 华，男，教授，博士生导师。

O38

2095-3828(2017)03-0081-05

A DOI 10.3783/j.issn.2095-3828.2017.03.014