基于轴心轨迹特征的发动机曲轴再制造性分析方法
王玉琳 胡锦强 柯庆镝 宋守许
合肥工业大学机械工程学院,合肥,230009
基于轴心轨迹特征的发动机曲轴再制造性分析方法
王玉琳 胡锦强 柯庆镝 宋守许
合肥工业大学机械工程学院,合肥,230009
运用主动再制造理论对再制造毛坯质量的不确定性进行了分析研究,提出了一种基于轴心轨迹特征的发动机曲轴再制造性分析方法。该方法通过运用不变矩算法提取同一发动机曲轴不同磨损状态下轴心轨迹的特征量,建立特征量与磨损量之间的映射关系,来判断发动机零部件的再制造性,从而实现对任意状态下曲轴磨损的量化。试验结果表明,运用该方法对曲轴磨损量进行识别具有较高的精度,为寻求曲轴服役期内最佳再制造时机提供了较为准确的判别依据,同时为服役期内伴随产品失效的同批次再制造毛坯质量的不确定性控制等问题提供了解决方案。
主动再制造;不确定性;轴心轨迹;曲轴磨损
0 引言
机电产品的再制造工程是以产品的全寿命周期设计和管理为指导,以实现性能跨越式提升为目标,以高效、优质、节能、节材、环保为准则,以先进技术和产业化生产为手段,对废旧机电产品进行修复与改造的一系列技术措施或工程活动的总称[1]。针对机电产品的再制造,国内外学者已提出了较多较完善的理论体系[2-3]。再制造的对象多为报废或即将报废的机电产品,其内部关键零部件的失效程度与失效状态均有很大的差异。有些零部件因过度或不当使用而造成失效状态的多样化,呈现较差的再制造性;还有一些零部件尚未达到再制造要求,若提前再制造,其内部潜在的使用价值就不能达到最大化利用,从而造成资源与能源的浪费。上述因素使得再制造毛坯在数量和质量上呈现较大的不确定性,最终造成再制造产品修复过程中的不确定性和复杂性,阻碍再制造技术的进一步工业化应用。
关于再制造毛坯质量不确定性的研究,国内外学者分别从不同的角度对其进行了探讨。MUKHOPADHYAY 等[4]研究了不确定性环境下不同回收品的质量等级对再制造策略的影响;DAS等[5]研究了制造与再制造混合系统的生产计划问题,通过建立混合整数规划模型确定最优的回收产品数量以及制造不同质量级别产品的数量;宋守许等[6]提出了基于寿命匹配的零部件再制造优化设计方法;刘长义等[7]提出了基于改进 BP 神经网络(BPNN)的发动机曲轴再制造平衡性质量控制方法。上述学者均是针对再制造毛坯质量的不确定性来寻求其质量控制方法的,他们多是研究报废后的产品质量控制,并未从源头上解决毛坯质量的不确定性问题。为此,刘光复等[8]提出了“主动再制造”这一思想,即在产品或零部件的整个服役周期内,存在一段最佳的再制造时间区域,在该区域内对其进行再制造,可实现其经济投入、技术要求以及环境排放等的综合最佳。
在对主动再制造的研究中,刘涛等[9-10]针对产品失效后被动再制造的现状,提出了面向主动再制造的可持续设计概念和模块化设计流程,形成主动再制造设计框架和模块优化;鲍宏等[11]针对主动再制造设计过程中的创新问题,提出了一种应用发明问题解决理论的主动再制造绿色创新设计方法;柯庆镝等[12]针对目前再制造毛坯数量及质量的不确定性问题,提出了基于性能参数的主动再制造时机抉择评价模型,以产品的全生命周期能耗为依据确定最佳主动再制造时间。
在对主动再制造的研究中,研究者多在产品结构设计之初考虑了再制造因素,却很少考虑再制造毛坯服役状态不确定性这一问题,即没有综合考虑产品在服役过程中的环境、平均服役时间以及工况等的差异性,从而导致再制造的时间点与实际的时间点存在较大差异。为了解决这一问题,本文首先阐述主动再制造的核心理念,同时以发动机曲轴轴心轨迹特征作为评价指标,通过建立评价指标特征与磨损失效间的映射关系,将任意服役状态下的特征与最佳再制造时机点对应的特征作对比,以此作为判断曲轴是否达到再制造要求的依据,从而提出了发动机曲轴再制造性的分析方法。
1 主动再制造理论
主动再制造是以保障产品原设计功能、性能为基本目标,以优质、高效、节能、节材、环保、产品总服役时间最长为准则,对正在使用的同一设计方案、同一批次生产的产品在一个适当的时间段内主动实施再制造的一系列工程活动[8]。其最大的特点在于“主动性”,即在产品服役过程中根据产品的性能退化,提前“主动”地分析在何时需要实施再制造,通过控制再制造毛坯质量以达到“最低投入、最大利用”的目的。现阶段的大部分再制造工程,基本可视为“被动”地进行再制造,完全是根据产品退役后的失效状态制订相应的再制造方案的。

图1 产品主动再制造时域和时机示意图Fig.1 Predecisional remanufacturing timing curve of product
图1为机电产品在服役过程中的性能退化及产品主动再制造时域与时机示意图。主动再制造的优势在于,理想状态下可使产品的使用寿命无限延长,尽可能提高其使用价值。主动再制造后产品总的使用价值Vu可用下式来表示:
(1)
式中,等号右边的第二项表示多次再制造后产品新增的使用价值;tAR为主动再制造的时间点;ti为产品第i次再制造修复后的寿命周期;n为再制造修复次数。
传统再制造对象包括产品级和零件级两大主要部分,根据主动再制造四大特征中关键零部件优先性原则[13],可将零部件作为主要研究对象。主动再制造的核心主要是研究再制造毛坯质量的不确定性问题,重点在于确定性能退化拐点(IP),在该点零部件失效程度大体一致,毛坯质量将在同一质量等级上,有益于进行大批量的再制造工程活动。零部件的失效量化指标一般为运行时间和失效程度,失效程度可通过计算转换为运行时间,但由于产品服役环境、环境与工况的差异性,导致由运行时间量化的拐点与实际的拐点存在较大的差异。为此,本文采用在线监测技术,将内部不易得到的失效状态运用监测手段予以表达,从而得以真实反映零部件的失效情况。
零部件的失效与外部监测信号具有一定的内在联系。零部件的主要失效形式包括疲劳破坏和磨损,其中磨损又是导致失效的最主要因素。在旋转机械中,磨损会导致零部件之间的配合间隙增大,产生碰撞、冲击和噪声等,而产品的振动与轴心轨迹的变化则是碰撞与冲击的外在表现。轴心与振动的变化可通过外部监测获取,分析信号的频谱特征以及轨迹的变化特征,便可建立特征与磨损失效间的映射关系,由该关系即可对零部件的失效状态进行判断,并可预测不同失效状态下的特征,为主动再制造的时机选择提供判断依据。
2 基于在线监测的再制造性分析
2.1 发动机曲轴再制造毛坯分析
发动机内部的关键零部件主要有曲轴、缸体与缸盖等。缸体与缸盖的服役寿命远远长于曲轴,所以对它们进行再制造性研究价值不高。曲轴是发动机中传递动力、承受冲击载荷的重要部件,其形状复杂,精度高,制造工艺繁琐,热处理和表面强化等要求严格,毛坯成本和加工费用也较高,通常情况下曲轴的失效多为磨损,再制造修复成本相对较低,因此曲轴具有较高的再制造价值。可将曲轴作为发动机主要零部件进行可再制造性分析,建立映射关系,以实现对曲轴磨损失效的定量识别。
再制造性识别方式有两种:一种是通过监测不同时刻的特征量运用映射关系了解其失效程度;另一种是通过映射关系掌握任意失效状态下的信号特征,为再制造的时机判断提供依据。对于某一零部件,在其性能退化拐点处的失效状态对应着一个磨损量σe,由映射关系得到对应该磨损量的一组特征量,当实测特征量与该组特征量信息相匹配时,即达到再制造要求。分析方案如图2所示,图中的Δσ表示主动再制造区域内σe两边的冗余磨损量。采用该方法进行再制造性判断,退役时的再制造毛坯的失效程度大体一致,质量被控制在同一等级上,可有效解决再制造毛坯质量的不确定性问题。

图2 再制造性分析方案Fig.2 Remanufacturing analysis program
2.2 基于在线监测的曲轴分析
曲轴的失效可以通过采用监测敏感部位的振动和轴心轨迹的变化等方法获取。在实际的振动信号监测中,敏感部位的选择直接影响采集信号的精准性,同时振动信号在传递过程中也会有一定的损耗,而轴心轨迹则能直观反映转子在轴承中的旋转和振动情况。当因磨损导致配合间隙变大时,连杆与曲轴间的碰撞便会加剧,轴心轨迹就会发生较大的偏移,在轨迹内部包含很多重要的特征信息,所以轴心轨迹特征的变化可作为表征曲轴失效的重要手段,以掌握曲轴的服役状态。
2.3 轨迹特征的提取
奇异值分解(singular value decomposition,SVD)算法具有良好的稳定性和不变性,其分解的奇异值能反映数据的内在属性,可以降低信号中的噪声,提高信噪比[14]。对于一个含有噪声的信号Y(N)={y1,y2,…,yN},通过相空间的重构构造m×n阶的Hankel矩阵Hm×n:
(2)
N=m+(n-1)
式中,Dm×n为无噪声干扰的信号子空间;Wm×n为噪声干扰信号子空间。

HU[17]的研究表明,图像的7个不变矩具有平移、比例、旋转的不变性,对形状变化十分敏感,可作为识别轴心轨迹的特征值。
原点矩
mpq=∬Rxpyqf(x,y)dxdy
(3)
中心矩
μpq=∬R(x-xc)p(y-yc)qf(x,y)dxdy
(4)
式中,R为轴心轨迹边缘区域;(xc,yc)为图像重心,xc=m10/m00,yc=m01/m00。
为确保中心矩相对于图像尺寸变化的不变性,对中心矩进行归一化处理。(p+q)阶归一化的中心矩
(5)
由上述公式得到7个HU不变矩:
(6)
这7个不变矩的数值变化范围较大,为便于数据的处理,取对数对7个不变矩数据进行压缩:
Ik=lg|φk|k=1,2,…,7
(7)
通过计算可得到7个改进的不变线性矩特征值,实现待识别图像集合到不变线性矩集合的映射。每一磨损状态下轴心轨迹图形均可由唯一的不变矩特征来表示,从而实现对轴心轨迹图形的识别。
3 轴心轨迹智能识别试验与分析
曲轴的主要磨损部位为主轴颈和连杆轴颈,由于连杆轴颈的润滑条件较差、负荷较大,其磨损比主轴颈更严重,且磨损后连杆与曲轴间的撞击程度即加剧,增大了对曲轴的冲击载荷,所以本文主要研究连杆轴颈的磨损。为了真实模拟曲轴的磨损,在发动机台架试验台上,对某型号单缸四冲程发动机进行曲轴磨损试验。在连杆轴径尺寸分别磨损0、0.09 mm、0.18 mm、0.27 mm、0.36 mm和0.45 mm时,通过两个互成90°的涡流传感器,监测曲轴在径向两处的位移变化,如图3所示。图3中的X、Y向标定处是两方向上的传感器。

图3 涡流传感器监测示意图Fig.3 Vortex sensor monitoring diagram
3.1 轴心轨迹的SVD降噪
发动机工况设定转速为2400 r/min,负载为12 N·m,采样频率为10 kHz。图4为发动机无磨损状态下X、Y处轴心方向上的时域波形。
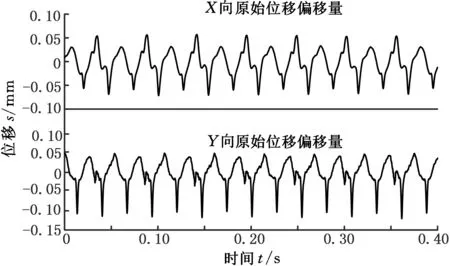
图4 原机无磨损时域波形Fig.4 Time domain waveform of original machine with no wearing
四冲程发动机完整的做功周期为2周,从各磨损状态下的时域波形图中截取512个点进行SVD降噪处理。重构的Hankel矩阵行数m分别取6、7、8、9、10、15,分析其分解后的奇异值分布。在各组截取数据中,当m≥8时,奇异值的变化相对较小,基本呈稳定变化的趋势;但当m=8时,前3个奇异值分量之和占据整体分量和的96%以上。综合考虑对各组数据降噪的效果,取m=8为轴心轨迹信号重构子矩阵的行数,所以构建的Hankel矩阵为H8×505。当m=8时,各组数据的前2次奇异值的能量与总体能量比达到98%,表明前2次的能量包含了信号的主体信息,根据前k次奇异值能量占优原则,取k=2为奇异值分解的有效阶次,完成轨迹的降噪处理。
3.2 轴心轨迹不变矩特征
经过SVD降噪后,由X、Y向的数据合成得到轴心轨迹,如图5所示。观察可知,在无磨损或磨损较小的情况下,在一个工作周期内轴心轨迹的形状较规则,因为在该磨损状态下,连杆与曲轴间的相对碰撞次数较少,对曲轴轴心轨迹影响较小;但随着曲轴磨损的加剧,因磨损导致的连杆轴瓦与曲轴轴颈间的配合间隙增大,使其在相对运转时的碰撞次数增多,最终结果是轴心轨迹向无规则形状变化,且轨迹更加集中,曲率半径不断减小,随着磨损量的增大,该特征愈加明显。这一明显变化,为监测及识别轨迹特征提供了可能。

(a)磨损量e=0
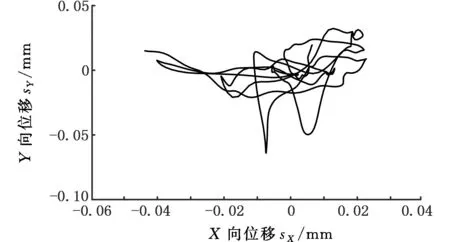
(b)磨损量e=0.36 mm图5 实测不同磨损状态的轴心轨迹Fig.5 Shaft center trajectory with different wear quantity
利用式(6)和式(7)对实测的轴心轨迹降噪数据进行处理,在不同磨损状态下,共有6组不变矩数值,经统计处理后样本的不变矩数值如表1所示。

表1 不变矩数值
有学者认为只有基于二阶矩的不变矩对二维物体的描述才真正具有旋转缩放和平移的不变性,其中I1与I2都是由二阶矩组成的,对不变性保持较好,而其余几个不变矩对图像的识别不敏感,效果不明显[18]。其中I1是轴心轨迹发散程度的度量指标,轨迹的发散程度越小,其值相对越小;而I2则是轴心轨迹对称性的度量指标,对称性越好,其值相对越小。其余不变矩对二维图像识别相对不敏感,在识别结果上存在一定误差,基于准确性考虑,本文选用前两个不变矩数值作为识别轴心轨迹的特征量。
比较轴心轨迹图形中轨迹的变化可以发现,随着曲轴磨损量的增大,其轨迹的对称性逐渐变差,离散程度逐渐降低且变得相对集中,且轨迹的曲率半径不断减小,究其原因是间隙的增大加剧了曲轴与连杆间的碰撞。再比较表1中不变矩数值的变化情况可以看出,随着磨损量的增大,不变矩I1的数值逐渐减小,I2的数值逐渐增大,表明随着曲轴磨损的加剧,其轨迹的变化特征与不变矩数值大小变化趋势具有一致性,这也形成了相互的验证,说明了数据的准确性。其余不变矩数值变化规律不明显且无明显的特征,对二维图像的特征识别不敏感,所以在本文中未作参考。通过不变矩数值I1、I2与磨损量e之间的变化规律,可构建磨损量与不变矩之间的映射关系。
将I1与磨损量e导入MATLAB中,应用最小二乘法进行曲线拟合,得到图6所示的拟合曲线;同时将I1、I2与磨损量e进行曲面拟合,得到图7所示的拟合曲面。曲面拟合的均方差为0.036 83,相关系数为0.9858,在误差允许范围内。运用该拟合方法,可以有效地减小多次拟合后产生的误差,在整体上提高磨损特征识别的精度。
磨损量与不变矩I1的关系为
(8)
磨损量与不变矩I1、I2之间的关系为
(9)

图6 磨损量与不变矩I1的关系Fig.6 Relationship between wearquantity and invariant moment I1

图7 磨损量随不变矩I1、I2的变化曲面Fig.7 Curve of wear quantity with the moment invariant I1 and I2
由主动再制造理论可知,曲轴在服役期存在一个最佳的再制造时机,该时刻对应一确定的磨损量eσ。根据式(8)可得到该磨损量下的特征值I1,用eσ去截取图7的变化曲面,即可得到该磨损量下对应的一组等高线(是关于I1、I2的相互关系),将通过式(8)得到的I1代入,即可算出该磨损量下的特征值I2。由文献[19]可知,曲轴主动再制造时发动机的服役时间为5.01年,曲轴年均磨损量约为0.066 mm,所以该型号发动机曲轴的最佳再制造时间所对应的磨损量e=0.33 mm,通过式(8)与截取的等高线,得到在最佳再制造时间点处所对应的特征量(I1,I2)=(0.681,1.2963)。当监测到某时刻的特征值达到或接近该值时,即可判断曲轴已达到了再制造的要求,此时进行再制造综合价值最大。
运用该映射关系即可实现对服役期内零部件磨损程度的识别,完成对零部件再制造时机的选择,不需要考虑零部件使用环境与工况等因素的差异,即可使退役时的零部件质量控制在同一等级上,解决了再制造毛坯质量的不确定性问题。
4 结束语
针对再制造过程中出现的再制造毛坯质量不确定性问题,运用主动再制造思想,通过模拟发动机关键零部件曲轴的磨损试验,提取原始轨迹信号,经SVD降噪后拟合出轴心轨迹,运用不变矩算法提取轴心轨迹图像的不变矩特征参量,构造出特征参量与磨损失效之间的映射关系,从而判断曲轴主动再制造时的服役状态,完成对其再制造性的分析。信号分析结果表明,该方法可有效应用于服役中的发动机曲轴,能够实时获取曲轴的再制造性状态,为实施发动机曲轴的主动再制造提供了技术保障。
[1] 徐滨士.再制造工程基础及其应用 [M].哈尔滨:哈尔滨工业大学出版社,2005. XU Binshi. Foundations and Applications of Remanufacturings Engneering[M]. Harbin: Harbin Institute of Technology Press,2005.
[2] 徐滨士,董世运,朱胜,等. 再制造成形技术发展及展望 [J]. 机械工程学报,2012,48(15):96-105. XU Binshi, DONG Shiyun, ZHU Sheng, et al.Prospects and Developing of Remanufacture Forming Technology [J]. Journal of Mechanical Engineering,2012,48(15):96-105.
[3] ZHU Sheng,MENG Fanjun,BA Dema. The Remanufacturing System Based on Robot MAG Surfacing [J]. Key Engineering Materials,2008,373/374:400-403.
[4] MUKHOPADHYAY S K,MA H.The Role of Quality Uncertainty in Remanufacturing Decisions [J].International Journal of Business and Systems Research,2009,3(4):387-412.
[5] DAS K,CHOWDHURY A H. Designing a Reverse Logistics Network for Optimal Collection,Recovery and Quality-based Product-mix Planning [J]. International Journal of Production Economics,2012,135(1):209-221.
[6] 宋守许,冯艳,柯庆镝,等. 基于寿命匹配的零部件再制造优化设计方法 [J]. 中国机械工程,2015,26(10):1323-1329. SONG Shouxu, FENG Yan, KE Qingdi, et al. Component Optimization Design for Remanufacturing Based on Life Matching [J]. China Mechanical Engineering, 2015,26(10):1323-1329.
[7] 刘长义,刘明周,刘从虎,等. 基于不确定性测度的再制造曲轴平衡性控制方法 [J]. 机械工程学报,2015(5):171-177. LIU Changyi, LIU Mingzhou, LIU Conghu, et al. Based on the Uncertainty Measure of Remanufactured Crankshaft’s Balance Control [J]. Journal of Mechanical Engineering,2015(5):171-177.
[8] 刘光复,刘涛,柯庆镝,等. 基于博弈论及神经网络的主动再制造时间区域抉择方法研究 [J]. 机械工程学报,2013,49(7):29-35. LIU Guangfu, LIU Tao, KE Qingdi, et al. Time Interval Decision-making Methods for Active Remanufacturing Product Based on Game Theory and Neural Network[J]. Journal of Mechanical Engineering,2013,49(7):29-35.
[9] 刘涛,刘光复,宋守许,等. 面向主动再制造的产品可持续设计框架 [J]. 计算机集成制造系统,2011,17(11):2317-2323. LIU Tao, LIU Guangfu, SONG Shouxu, et al. Product Sustainable Design Framework Active Remanufacturing [J]. Comuter Integrated Manufacturing Systems,2011,17(11):2317-2323.
[10] 刘涛,刘光复,宋守许,等. 面向主动再制造的产品模块化设计方法 [J]. 中国机械工程,2012,23(10):1180-1187. LIU Tao, LIU Guangfu, SONG Shouxu, et al. Product Modular Design Method for Active Remanufacturing [J]. China Mechanical Engineering, 2012,23(10):1180-1187.
[11] 鲍宏,刘志峰,胡迪,等. 应用TRIZ的主动再制造绿色创新设计研究 [J]. 机械工程学报,2016,52(5):33-39. BAO Hong, LIU Zhifeng, HU Di, et al. Research on Green Innovation Design Method of Active Manufacturing Using TRIZ [J]. Journal of Mechanical Engineering, 2016,52(5):33-39.
[12] 柯庆镝,王辉,刘光复,等. 基于性能参数的主动再制造时机分析方法 [J]. 中国机械工程,2016,27(14):1899-1904. KE Qingdi, WANG Hui, LIU Guangfu, et al. Timing Decision-making Analysis Method for Proactive Remanufacturing Based on Performance Parameters[J]. China Mechanical Engineering, 2016,27(14):1899-1904.
[13] 宋守许,刘明,柯庆镝,等. 基于强度冗余的零部件再制造优化设计方法 [J]. 机械工程学报,2013,49(9):121-127. SONG Shouxu, LIU Ming, KE Qingdi, et al. Components Optimization Design for Remanufacturing Based on Residual Strength[J]. Journal of Mechanical Engineering,2013,49(9):121-127.
[14] 何志坚,周志雄. 基于FSWT细化时频谱SVD降噪的冲击特征分离方法 [J]. 中国机械工程,2016, 27(9):1184-1190. HE Zhijian, ZHOU Zhixiong. Impact Feature Separation Method Based on FSWT Zoom Time-frequency Spectrum Denoised by SVD [J]. China Mechanical Engineering, 2016,27(9):1184-1190.
[15] 张永祥,王孝霖,张帅,等. 基于奇异值分解和相关峭度的滚动轴承故障诊断方法研究 [J]. 振动与冲击, 2014,33(11):167-171. ZHANG Yongxiang, WANG Xiaolin, ZHANG Shuai, et al.Rolling Element Bearing Fault Diagnosis Based on Singular Value Decomposition and Correlated Kurtosis [J]. Journal of Vibration and Shock,2014,33(11):167-171.
[16] 赵海峰,张亚,李世中,等. 基于奇异值分解的侵彻过载信号降噪方法 [J]. 振动、测试与诊断,2015,35(4):770-776. ZHAO Haifeng, ZHANG Ya, LI Shizhong, et al. Penetrating Overload Signal Denoising Method Based on Singular Value Decomposition [J]. Journal of Vibration Measurement and Diagnosis,2015,35(4):770-776.
[17] HU M K. Visual Pattern Recognition by Moment Invariants [J]. Information Theory Ire Transactions on,1962,8(2):179-187.
[18] 史东锋,屈梁生. 轴心轨迹定量特征提取技术在回转机械诊断中的应用 [J]. 化工机械,1999(1):25-28. SHI Dongfeng, QU Liangsheng. Application of Axial Trajectory Quantitative Feature Extraction Technology in Rotary Machinery Diagnosis[J]. Chemical Machinery, 1999(1):25-28.
[19] KE Qingdi, WANG Hui, SONG Shouxu, et al. A Timing Decision-making Method for Product and Its Key Components in Proactive Remanufacturing [J]. Procedia Cirp, 2016, 48:182-187.
(编辑 袁兴玲)
Remanufacturability Analysis Method for Engine Crankshafts Based on Shaft Center Trajectory
WANG Yulin HU Jinqiang KE Qingdi SONG Shouxu
School of Mechanical Engineering,Hefei University of Technology,Hefei,230009
The uncertainty of the remanufacturing blank qualities was analyzed by the theory of predecisional remanufacturing. A remanufacturability analysis method was presented based on shaft center trajectory. This method extracted the characteristic parameters of the shaft center trajectory of the same engine crankshaft under different wear conditions by using the moment invariant algorithm. The mapping relationship among the characteristic quantity and wear quantity was established to determine the remanufacturability of the engine parts so that the quantification of crankshaft wear under any conditions might be realized. The test results show that the method has high precision for identifying the wear of the crankshafts. It provides a more accurate criterion to find the optimal remanufacturing time in the service period of the crankshaft. At the same time, it provides a solution to the uncertain control problems of remanufacturing blank qualities in the service period with the same batch product failures.
predecisional remanufacturing;uncertainty;shaft center trajectory;crankshaft wear
2016-07-25
国家自然科学基金资助项目(51305119,51375133)
TH122
10.3969/j.issn.1004-132X.2017.13.014
王玉琳,男,1966年生。合肥工业大学机械工程学院副教授、博士。研究方向为机电产品回收与再利用。胡锦强,男,1990年生。合肥工业大学机械工程学院硕士研究生。柯庆镝(通信作者),男,1984年生。合肥工业大学机械工程学院副教授、博士。E-mail:qingdi.ke@hfut.edu.cn。宋守许,男,1964 年生。合肥工业大学机械工程学院教授、博士。

