基于两阶段法的车辆配载优化分析

王鹤+曾宁波+刘婧雯

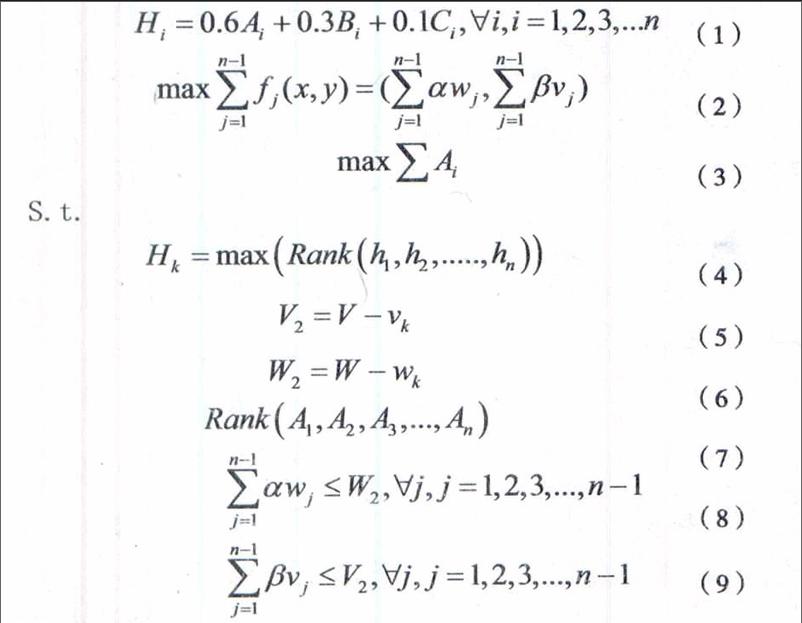
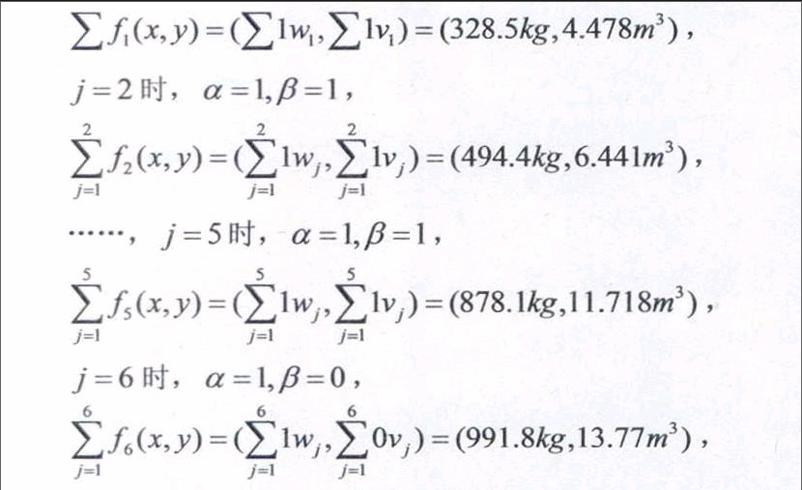
摘要：本文从降低物流配送成本，提高车辆利用率的角度出发，综合考虑车辆的额定容积与载重、订单价值等多重因素，建立了相应的决策模型，并设计了改进的两阶段法和0-1型整数规划进行决策方案的求解，将此模型实际运用到某小家电制造商的车辆配载过程中，对比结果分析表明，该优化模型不仅能提高车辆利用率，更能大幅提升物流配送利润。该模型结果对车辆配载的优化研究具有一定借鉴意义。

关键词：车辆配载；订单分析；两阶段法；0-1型整数规划

中图分类号：F252 文献标识码：A

文章编号：1005-913X（2017）06-0036-03

一、引言

随着物流行业的蓬勃发展，物流配送领域的不断扩大，车辆资源的利用率问题逐渐成为物流管理人员一大关注点。据中国物流信息中心物流统计数据表明，发达国家的物流费用占国民生产总值（GDP）的比重远低于10%，而我国这一项数据已攀升至17.8%，约为发达国家的两倍，物流费用的持续攀高使得企业的资金运转压力增大。同时，我国市场上一般物流企业的车辆平均载重率为75.67%，车辆平均容积率仅65.37%，大量车辆资源的浪费导致企业管理成本增加。显然，配送成本和管理成本作为物流成本中占比最大的一项，降低这两类成本将引起物流成本增速的放缓，直接提高物流配送利润，为企业带来更大的运营效益。此前，有不少关于优化车辆配载模型的研究。如刘铁男（2014）通过对车辆的判断和对货物的特性分类，运用贪婪算法建立物流车辆配载模型进行有效的拼装组合，实现车辆的载重和容积利用程度达到最大，结果显示，可以大力的节省运力，节省物流企业的配送成本。[1]谢天保（2010）等将染色体的进化过程运用到遗传算法求解中，在任务时间窗和车辆实际容量的约束条件下建立车辆配载调度模型，最后通过实验分析证明运用该模型快速求解最优解，且结果具有一定的借鉴意义。[2]曹明兰（2009）等为保证配货中的稳定客源，通过设立顾客紧急系数，运用二阶段法，分别在不同阶段实现不同的目标，最后建立能够实现满足客户需求目标的能使车辆得到充分利用的车辆配载模型。[3]胡贵彦等通过对传统型配载模型的优化，将配载车辆分成平面的分别有约束条件的四个放置区，利用计算机编程技术，开发了能使空间利用率达到最优的视窗软件，传统模型与优化模型对比可知，优化模型可大幅提高车辆的空间利用率。[4]杨锦冬（2004）等从车辆驾驶员和物流企业的双角度出发，在约束条件下，利用0-1整数规划建立了一个配送配载双目标优化模型，实现了配送路径最短，拼装方案最优的目标，仿真实验证实了该模型的可行性。[5]Liu（2016）等考虑在带时间窗和装载车辆的约束条件下，运用改进的分支定界方法和贪婪算法建立车辆配载的优化模型，结果表明，其模型能够提高整车物流的配载效率。[6]

上述文献是假设在车辆的承载能力的约束下，以满足客户要求和配送成本最小为目标建立模型，没有考虑到交货期、配送时间及利润等方面的影响，虽然这样的模型能够最大限度的利用车辆的容积和载重，满足客户浅层次的要求级按时交货，这样不仅忽视了所要配送的订单优先级别，不能够在提高车辆利用率的同时做到重要的訂单优先配送，并且未将所配送的订单价值作为影响因素考虑进去，这样所带来的问题是提高了利用率的同时降低了客户满意度，并没有达到最佳效果。因此，本文运用两阶段法以及0-1型整数规划，分阶段合理设置目标函数及变量、参数，第一阶段考虑了订单优先度大小问题，确定必须优先配送的订单，做好客户管理，维系好客户关系；第二阶段考虑了车辆容积、载重的利用率和订单价值问题，将订单价值作为主要因素，在其排序结果及车辆的核定容积与载重的约束下，确定最终的车辆配载方案，使车辆利用率得到提高，配送成本下降，不同程度的提升配送利润。

二、基于车辆配载优化问题的建模

（一）建模前提

可以将车辆的配载优化问题描述为：针对制造商所接到的订单，选择最佳的车辆配载方案，在一定的约束条件下，诸如所要配送的订单交货期一定，均能满足客户的按时交货要求，且一个订单至少包括一种货物，同一订单的货物由同一次车辆进行配送，每件货物的实际容积和重量在车辆的承受范围之内，不存在超载现象，同时，所有待配载的订单为原始订单，未经后期的加工处理，无插单、割单等，使物流企业在高度满足客户要求，配送的订单价值达最大，车辆利用率提高，提升配送利润。

（二）符号说明

决策参数：

i为订单编号，i=1，2，3......n；Hi为订单优先度，i=1，2，3......n；Ai为单个订单的订单价值量，i=1，2，3......n；Bi为制造商对客户的预测订单月交易量，i=1，2，3......n；Ci为订单的客户重要程度，i=1，2，3......n；根据唐丽春，蔡晓毅（2009）在供应链环境下对影响订单优先权的因素所采用的线性归一化的处理结果将Ai，Bi，Ci的系数分别设为0.6，0.3，0.1；W2，V2为第一阶段配载货物后车辆的剩余容积和载重，W2=W-wk，V2=V-vk，是第二阶段配载的限制变量；j表示将第二阶段订单的计算看作不同的计算步骤j=1，2，3......n-1；Wj，Vj分别为第二阶段进行到第j步时，所装载的容积和载重；x，y为第二阶段车辆中装入货物总重量和总容积；αwj，βvj取决于下面的决策变量。

决策变量：

α1累加订单容积及载重≤W

0 否则，

β1累加订单容积及载重≤V

0 否则，

（三）车辆配载优化模型

建立的车辆配载优化模型如下：

式（1）为第一阶段的目标函数，式（2）式（3）为第二阶段目标函数，表示在已知订单优先度的前提下，满足约束条件的车辆利用最优化，订单价值最大化。式（4）至式（9）为模型的约束条件，式（4）表示第一阶段选出来的订单，其订单优先度必须为最高，式（5）式（6）表示第二阶段的容积载重不得超过车辆的核定容积载重，式（7）表示第二阶段初始必须对订单价值进行排序处理，式（8）式（9）表示第二阶段累加计算的订单容积和载重不得超过第二阶段剩余容积和载重。

三、算法描述

为了更好的实现车辆配载优化，提高物流企业单次配送利润，本文采用两阶段法和0-1型整数规划相结合的算法构建优化模型。

第一阶段：当制造商接收到一批需要配送的订单集合1，2，3，...，n时，整理其所有的订单数据，确定每个订单的订单价值Ai，月交易量Bi和客户重要程度Ci，据式（1），对这三个指标分别给予不同的权重，可得每个订单的订单优先度数值。根据数值结果，将数值最大的订单确定为第一阶段必须配载的货物订单k。

第二阶段：在求出订单的基础上，可知车辆剩余容积和载重W2，V2。同时，对剔除后的订单集合1，2，...，k-1，k+1，...n进行以订单价值为关键词的排序处理，第二阶段的计算在此排序结果的前提下进行。将剩余的n-1个订单看成不同的n-1个计算步骤，根据式（8）式（9），对0-1型变α，β量分別进行取值计算，即可求得从订单k开始累加的车辆容积与载重wi，vi直至累加达到maxf（x，y）即式（2）时，计算停止，可以得到最佳的配载方案P=1，...，k，...，n使得车辆利用率最大化，配送利润得到不同程度的提升。

四、算例分析

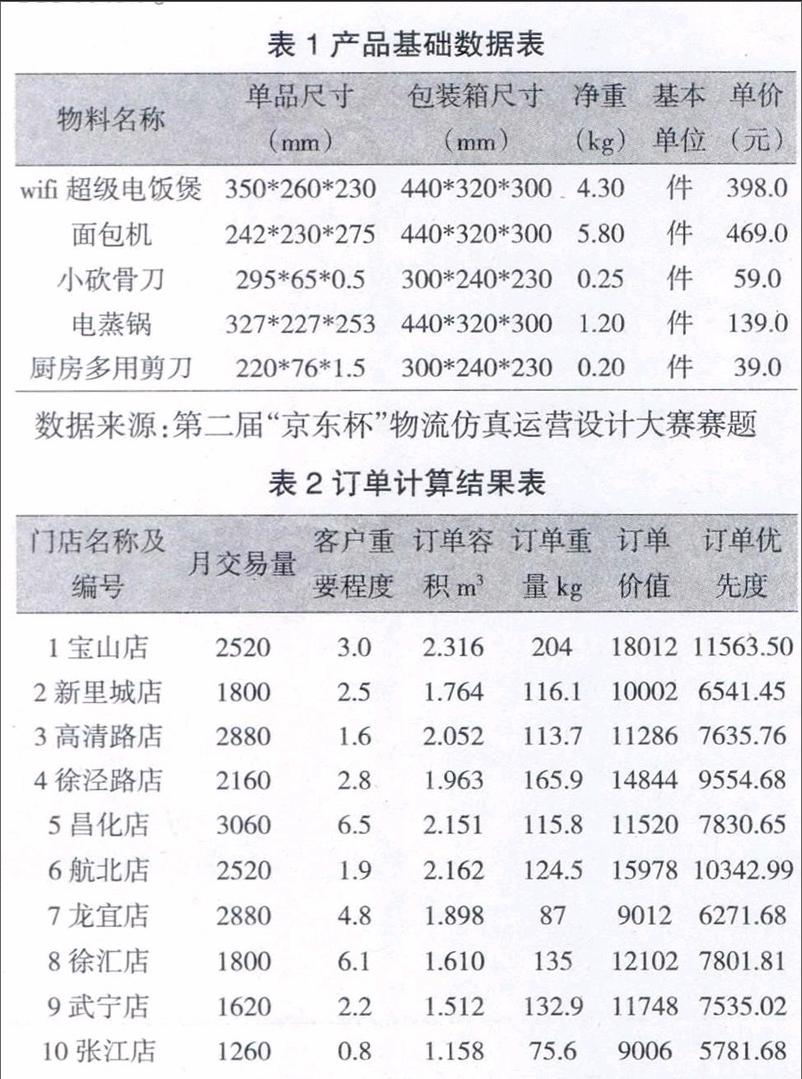
在本算例中，由于制造产品均为小家电，因此，假设使用一辆额定载重为1.5t，容积为12m3的轻型配送车辆进行配载。以某家电制造企业2016年6月份其中两天的订单数据为例，订单产品的基础数据如表1所示，分别统计来自十家门店订单的货物容积、重量以及订单价值。

第一阶段，由式（1）Hi=0.6Ai+0.3Bi+0.1Ci计算可得十个订单的订单优先度，计算结果如表2所示。对此结果进行排序，由式（3）很明显的可以看出，必须优先配送的订单1，来自宝山店，其订单优先度为11563.50。

第二阶段，确定好第一阶段必须配送的订单的容积为2.316m3，重量为204kg后，可以求得车辆的剩余载重W2=1296kg，剩余容积V2=9.684m3。据式（6），对其他订单进行以订单价值为关键词的排序，如表4所示。由第二阶段目标函数式（2）可得，当j=1时，α=1，β=1即

显可以看出，经过6个步骤后，可以求得此规划问题的最优解即最佳车辆配载方案为1、4、5、6、8、9，该方案的订单容积量为11.718m3，重量为878.1kg，车辆的容积利用率和载重利用率分别为98%和59%，配送的订单价值达高达77753.5元。

同时，为了更显著的比对出模型的优化效果，通过计算机程序语言，以车辆核定容积为主要的约束条件，对所有订单进行随机组合，共有141120种组合结果，选取到其中结果最佳的随机组合方案为订单1、2、3、5、7、8，计算可得此随机方案的车辆容积载重利用率，可知其配送的订单价值大小，具体的比对结果如表4所示。

由表4可以看出，虽然随机方案的容积利用率为99%，比优化方案高1%，但在车辆的载重率以及单次配送的订单价值上，优化方案都略胜一筹，配送的订单价值更是比随机方案要多1746元。在物流公司的实际运营过程中，提高现有车辆资源的利用率固然重要，但流动资金对一个公司生产经营起着决定性力量，如何使配送利润得到提升，配送成本不断降低同样受到关注。因此，在对比结果的时候不能单独比较车辆利用率的浮动，应该更加关注订单价值即单次配送利润的大小。显然，从结果分析可知，优化模型的结果是可行的，具有一定借鉴意义。

五、结语

本文通过研究分析物流企业的车辆配载过程车辆的利用率过低以及配送成本偏高的问题，建立了两阶段法和0-1型整数规划的相结合双算法优化模型。该模型综合考虑到了影响订单和物流服务的多个因素，如订单优先度，订单价值，车辆有效容积、重量等。在加强客户合作关系的同时，提高物流企业车辆利用率，实现了车与货的高效匹配，大幅提升了企业配送利润，降低了配送成本。在实证研究中，以某家电制造企业为例，计算了订单的增量订单价值以及车辆容积重量利用率，并通过计算机程序，科学选取了随机方案进行对比，研究结论对优化车辆配载有一定的指导意义。

参考文献：

[1] 刘铁男.贪婪式算法在在物流配送车辆配载模型中的应用[J].物流技术，2014，33（10）.

[2] 谢天保，雷西玲，席文玲.物流配送中心配载车辆调度研究[J].计算机工程与应用，2010，46（36）.

[3] 曹明兰，郎茂祥，曹明琴，乔晓东.考虑客户需求优先级的货物配装问题的模型与算法研究[J].物流科技，2006（29）.

[4] 胡贵彦，杜志平，孙卫华，钟芙蓉.货物配载方法最优化的研究[J].物流技术，2009，28（8）： 86-107.

[5] 杨锦冬，徐丽群.城市物流中心车辆配送配载调度指派模型研究[J].同济大学学报：自然科学报， 2004（11）.

[6] Liu J S，Alice E S，Dan Q. The vehicle loading problem with a heterogeneous transport fleet[J]. Computers & Industrial Engineering.2016，97： 137-145.

[7] 靳志宏，于 波，侯丽晓.基于配载约束的配送优化问题及其求解算法[J].系统工程学报，2012（3）.

[8] 孙国华.带时间窗的开放式满载车辆路径问题建模及其求解算法[J].系统工程理论与实践，2012，32（8）.

[9] 朱 伟，徐克林，佀占华，周 娜.单车辆物流配送决策模型及其遗传算法[J].同济大学学报：自然科学版，2011（6）.

[10] 包得海，管会生.一种求解货物配送问题的改进算法[J].湖南师范大学自然科学学报，2011（5）：12-16.

[责任编辑：谭志远]