基于改进型神经网络模型的负荷短期预测仿真研究
万 江,周 臖,梁 伟,郑继红,李 龙,李登峰
(1.国网重庆市电力公司重庆电力调控中心,重庆404100;2.国网重庆市电力公司南岸供电公司,重庆404100;3.国网重庆市电力公司重庆电力科学研究院,重庆404100)
基于改进型神经网络模型的负荷短期预测仿真研究
万 江1,周 臖2,梁 伟1,郑继红1,李 龙3,李登峰3
(1.国网重庆市电力公司重庆电力调控中心,重庆404100;2.国网重庆市电力公司南岸供电公司,重庆404100;3.国网重庆市电力公司重庆电力科学研究院,重庆404100)
选择BP人工神经网络作为电力系统负荷预测的模型,发现其具有收敛速度较慢,且容易陷入局部最小的缺点。因此,引入拟牛顿法和附加动量法对其性能进行改进,并形成一种改进型的预测模型。以重庆市某供电公司供区为背景,利用其负荷数据进行仿真,结果证明,对BP人工神经网络的改进是成功的。这种方法可以更好地满足电力负荷短期预测的精度要求,对电力系统控制、运行和规划都具有重要意义。
短期负荷预测;神经网络;BP算法;拟牛顿法;附加动量法
电力系统短期负荷预测的精度对于电力系统的安全、经济和可靠运行起着至关重要的作用。在多种因素影响下,负荷的变化具有复杂性、非线性等特征。由于负荷预测的误差会导致运行和生产成本的增加,因此,提高负荷预测的精准度对电力系统控制、运行和规划都具有重要意义。
本文选择BP人工神经网络作为电力系统负荷预测的模型。通过对BP人工神经网络的分析,发现其具有收敛速度较慢,且容易陷入局部最小的缺点。因此,引入拟牛顿法和附加动量法对其性能进行改进,并形成一种改进型的预测模型。最后,以重庆市某供电公司供区为背景,利用其负荷数据,对BP人工神经网络、拟牛顿法神经网络、附加动量法神经网络及改进型神经网络进行负荷预测仿真。以此证明,通过对BP人工神经网络进行改进,能够提高电力负荷短期预测的精度。
1 BP神经网络的特点
1.1 分布式的信息存储方式
神经网络的某一部位不是只存储了一个外来的信息,而是存储了多个信息的部分内容。作为一种分布式的信息存储方式,多个信息通过加工之后,被存储于网络的各个部位。
1.2 大规模并行处理
BP神经网络信息的计算处理与存储是合为一体的,信息的存储方式体现在神经元相互连接分布上,且通过大规模的并行分布方式计算为主,在这一点上,要优于串行离散符号处理的现代数字计算机。
1.3 自适应和自学习性
BP神经网络各层直接的连接权值具有一定的可塑性,网络的权值可通过学习和训练来得到,其对外界事物的自动学习能力及对外部环境的适应能力较强。
1.4 容错性和鲁棒性强
BP神经网络具有较强的联想记忆功能和鲁棒性。当某部分信息损坏或者遗失,网络仍然能够复原完整的信息,维持系统运行[1]。
2 BP神经网络学习参数的选择
2.1 阈值和权值的初始值选择
神经网络阈值和权值的初始值均与训练时间长短、收敛速度的快慢及网络训练的结果相关。初始值选择过大,网络的调节过程将减缓。为了能在最大范围内对各个神经元的权值进行相应的调节,必须使神经元在初始加权后的输出值均趋于零,通常情况下,初始值在(-1,1)区间里。
2.2 学习率的选择
学习率的选择范围一般在(0.01,0.7)区间内,对于不同的误差曲面,学习率也可能不同。权值调整公式如式(1)所示。

式中:ΔW(n)为权值的调整量;E为误差;W(n)为连接权值;α为学习率,其值的高低直接影响神经网络的收敛速度[2]。
2.3 动量项的选择
为了做到既能提高收敛速度,又能减小收敛振荡,最直接的方法就是引入“动量项”,如式(2)所示。

将式(2)转化为误差形式,如式(3)所示。

将样本值依次加入式(3),该式可变化为时间序列形式,时间t的区间为0到n。因此,可将式(3)当作是Δwij(n)的一阶差分方程,对Δwij(n)进行计算可得

式(4)中,与前一次正负不相同时,加权结果会使得Δwij(n)较小,因此有利于整个网络的收敛稳定;而当与前一次正负相同时,加权求和结果会随之增大,使得Δwij(n)较大,加快了w的变化速度。
2.4 期望误差的确定
期望误差值的适合与否,取决于隐含层的神经元的个数。如果隐含层中神经元个数越多,则期望误差越小。假设神经网络的误差界值Emin为0.001~0.01,当计算出的误差值ε<Emin时,认定学习过程结束,计算终止,输出结果。当训练次数较大导致不能收敛时,此时需要将Emin值设定得大一些,并且限制其训练次数;若训练次数完毕,计算结果还未收敛到误差界值,则放弃本次计算[3-4]。
3 改进型负荷预测模型构造
每个预测模型考虑的影响因素是不同的,这是由于出发点和建模机制的不一样,每个预测模型都不能完全反映负荷变化规律,在负荷预测中仅能表现出部分问题。针对此情况,本文在基于BP神经网络模型的基础上提出一种改进型的负荷预测模型,即通过建立多个单一的神经网络模型,然后选择适当的权重组合在一起,组合成神经网络短期负荷预测模型。
3.1 模型改进依据
本文假设选择了n个独立的子模型,其中第i个子模型gi(x)的绝对误差为εi=g(x)-gi(x)。其中,g(x)表示实际数值的模型,则第i个子模型预测的均方误差可表示为式(5)。

假设各εi(x)之间相互独立,且均值为0,则组

从式(8)可得,将n个相互之间毫无联系的预测模型组合而得到新的预测模型,其预测的均方误差变为原来子模型均方误差。将多个不同的预测子模型按照需求进行恰当的组合,利用各种模型的特点,能有效提高预测精度。
3.2 BP算法子模型结构的改进
BP神经网络计算方法具有收敛速度较慢,且容易陷入局部最小的缺点。因此,我们利用拟牛顿法和附加动量法对典型的BP算法子模型进行改进。
3.2.1 拟牛顿法神经网络子模型
牛顿法是在标准梯度法上作了一定改进,利用准则函数在搜索点的梯度和它的二次导数,及搜索点所能提供的信息,优化搜索方向使之尽快找到最优点。其迭代公式如式(9)所示[5]。

式中:k为迭代步骤;gk为第k次迭代的梯度信息;Hk表示第k次迭代的二阶导数矩阵(Hessian矩阵);H-1k为第k次迭代二阶导数矩阵的逆矩阵;wk+1和wk分别表示第k+1次、第k次迭代的权值。
从式(9)可知,在计算过程中,拟牛顿法每次迭代都需要对二阶导数矩阵进行求解。因此,计算过程比较复杂。为了降低其计算的复杂程度,笔者通过利用近似值来更新二阶导数矩阵,更新值为梯度的函数。这样,就可以省略重复计算二阶导数矩阵及其逆矩阵的过程,这就是拟牛顿法。
拟牛顿法采用BFGS公式来对二阶导数矩阵进行修正,如式(10)所示。合预测模型gAV(x)的预测均方误差如式(8)所示。

式中:ΔE(wk+1),ΔE(wk)分别表示第k+1次迭代和第k次迭代网络目标函数的梯度向量;wk+1,wk分别表示第k+1次迭代和第k次迭代的网络权值。
3.2.2 附加动量法子模型
附加动量法子模型的拓扑结构也是采用单隐层的前馈神经网络,学习算法采用附加动量法(AM算法)。一般的前馈神经网络的学习算法常采取标准BP神经网络算法,其本质上是一种最速下降寻优算法,其权值的更新是沿着当前时刻负梯度方向进行的,权值修正如式(13)所示。

式中:ηδjOki表示权值更新量;δj表示训练样本的一般误差;Oki表示第k个样本第i个节点的输出量;η为学习率;wjt(t+1)表示第i+1次迭代权值的更新后的值;wjt(t)表示第t次迭代权值更新前的值。
通过式(13)可以得出,标准BP算法对新样本的学习过程常常存在收敛速度较慢和存储状态不稳定的缺点。在对权值进行修正时,附加动量算法不仅要将最后一次权值的变化,通过一个动量因子传递到本次误差计算所得的权值更新量上,而且作为此次实际权值更新的一个组成部分,还会考虑在负梯度方向上对误差的影响。附加动量算法如式(14)所示。

式中:αΔwjt(t)表示动量项;wjt(t)为第t次迭代的权值修正量;α为动量(0<α<1)。
由式(14)可知,附加动量算法在权值更新时,充分考虑了在误差曲面及梯度上变化趋势的影响,减小了学习过程中的振荡趋势,有效抑制了网络陷入局部极小,达到了改善算法收敛性能的目的。
3.2.3 改进型BP神经网络
本文运用一个时变权系数,将基于拟牛顿法和基于附加动量法的BP神经网络子模型进行加权组合,形成一种改进型的BP神经网络预测模型,如图1所示。

图1 改进型BP神经网络预测模型
图1中,a1(t),a2(t)分别为改进型BP神经网络模型的权值系数。
改进型预测模型可用式(15)表示。

式中:y(t)表示改进型模型t时刻的负荷预测值;yi(t)表示在t时刻的第i个子模型的负荷预测值。
假设该改进型预测模型由n个单一子模型构成,其中,单个预测日中含有N个时刻的负荷,在t时刻的第i个(i=1,2,…,n)子模型ai(t)的时变权系数满足条件,如式(16)所示。

式中:Y(t)表示t时刻的实际负荷值。
4 针对重庆某供区负荷的仿真分析
4.1 某供区日电力负荷曲线分析
调用SCADA系统数据库中某供区2015年9月18日的负荷历史数据,绘制出该地区工作日内的负荷变化曲线如图2所示。
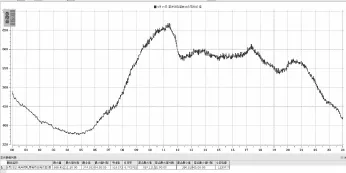
图2 某供区日负荷曲线图
该供区当日负荷不同时刻的变化规律呈“三峰两谷”趋势,其日用电负荷大小与当地生产作息时间及生活规律有着密不可分的联系。某电网负荷基数小,夏季降温负荷大,地区电网管理面积广,是制约负荷预测合格率的三大因素。
4.2 改进型预测模型仿真预处理
4.2.1 样本构造
输入量:预测日与其前一天的某个相同时刻以及邻近时刻的负荷共3个,预测日前5天总共为15个;预测日前5天的最高、最低、平均气温共15个;预测日当天的最高、最低、平均气温共3个。总共33个输入。
输出量:预测日某一时刻的负荷共1个。
4.2.2 数据归一化处理
为了避免神经元出现饱和,提高预测的准确度,使输入负荷数据位于(0,1)之间,须采用式(18)对t时刻的负荷数据进行归一化处理,用y表示。

式中:Xmax,Xmin表示训练样本集合中电力负荷的最大值和最小值。
4.2.3 天气样本处理
气温的隶属度函数高温采用偏大型梯形分布,中温采用中间型梯形分布,低温采用偏小型梯形分布。
高温的隶属度函数为

分别对同类型日的最高温度以及最低温度代入以上面公式,计算得到其对应的低、中、高3个状态的隶属度及其取值。
4.2.4 预测执行步骤
改进型神经网络预测模型的预测执行步骤如图3所示。
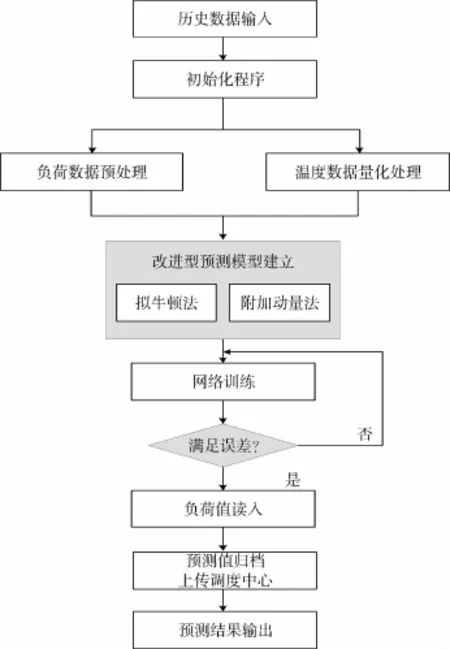
图3 负荷预测执行步骤
4.2.5 改进型BP神经网络预测模型在短期负荷预测中的仿真结果
本仿真所有子模型均为只含有一个隐含层的BP神经网络,神经网络的输入层数均为33,隐含层数均为66,输出层均为1,因此神经网络结构为33-66-1。
本次仿真测试选用训练样本数为60。参数设置:动量因子为0.9,学习率为0.01,训练次数为10 000,训练目标为0.001。针对2015年5月13日某供电公司供区负荷,分别采用标准BP神经网络预测模型、拟牛顿法神经网络预测模型、附加动量法神经网络预测模型及改进型神经网络预测模型进行仿真。其负荷预测如图4~7所示。

图4 BP神经网络预测模型下的实际值与预测结果图型
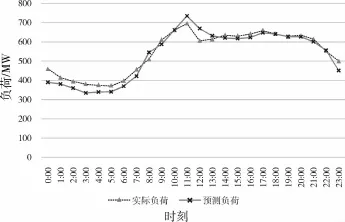
图5 拟牛顿法神经网络模型下的实际值与预测结果图

图6 附加动量法神经网络模型下的实际值与预测结果图

图7 改进型神经网络模型下的实际值与预测结果图
误差分析如图8~11所示。

图8 BP神经网络预测模型下的误差分析图

图9 拟牛顿法神经网络模型下的误差分析图

图10 附加动量法神经网络模型下的误差分析图

图11 改进型神经网络模型下的误差分析图
改进型BP神经网络预测模型的预测误差是最小的,平均误差和最大误差分别比标准BP神经网络预测模型降低了1.76%和12.84%,如表1所示。

表1 四种预测模型的误差分析数据对比
5 结论
本文主要介绍将改进型的BP神经网络负荷预测模型应用于某供电公司供区的情况。通过分析某公司供区负荷的实际情况及特点,利用本文所提的4种模型,分别对其进行预测仿真和测试,证实所提出的改进型预测模型能有效提高预测准确度,最适合某供电公司所辖供区的负荷情况,如将其作为实际电网短期负荷预测软件的预测子模块,理论上能满足实际的短期负荷预测要求。
[1] 康重庆,夏清,张伯明.电力系统负荷预测研究综述与发展方向的探讨[J].电力系统自化,2004,25(17):1-11.
[2] MOGHRAM I,RAHMAN S.Analysis and evaluation of five short term load forecasting techniques[J].IEEE Transactions on Power Systems,1989,4(4):1 484-1 491.
[3] 杨争林,宋燕敏,曹荣章,等.短期负荷预测在发电市场中的应用[J].电力系统自动化,2000,24(1):14-17.
[4] 欧建平,李丽娟.人工神经网络在电力系统短期负荷预测中的应用[J].广东电力,1999,30(2):4-7.
[5] ANGELINE P J,SAUNDERS G M,POLLACK J B.An evolutionary algorithm that constructs recurrentneuralnet works[J].IEEE Transactions on Neural Networks,1994,5(1):54-65.
A Simulation Study on the Short Term Load Forecasting Based on An Im proved Neural Network M odel
WAN Jiang1,ZHOU Jun2,LIANGWei1,ZHENG Jihong1,LILong3,LIDengfeng3
(1.Chongqing Electric Power Regulation and Control Center of State Grid Chongqing Electric Power Company,Chongqing 404100,P.R.China;2.Nan an Power Supply Branch of State Grid Chongqing Electric Power Company,Chongqing 404100,P.R.China;3.Chongqing Electric Power Research Institute of State Grid Chongqing Electric Power Company,Chongqing 404100,P.R.China)
The BP artificial neural network was chosen as themodel for load forecasting in the power system,but its rate of convergence was slow and it easily fell into a localminimum.The quasi newton method and the additional momentum method were used to improve its performance and an improved forecastingmodelwas formed.Taking the service area of a power supply branch of State Grid Chongqing Electric Power Company for example,the simulation was implemented by using its load data,the result of which proved that the improvement of the BP artificial neural network was successful.Thismethod can meet the demand for the accuracy of the short term load forecasting and is significant in the control,operation and planning of power system.
short term load forecasting;neural network;BP algorithm;quasi newton method;additional momentum method
TM715
A
1008 8032(2017)03 0031 06
2017-02-08
万 江(1983-),高级工程师(副高级),研究方向为电力系统分析运行。

