基于FVFACM的JV肺结节分割

刘丽伟， 王国明

(长春工业大学 计算机科学与工程学院， 吉林 长春 130012)



基于FVFACM的JV肺结节分割

刘丽伟， 王国明*

(长春工业大学 计算机科学与工程学院， 吉林 长春 130012)

对几种活动轮廓模型肺结节分割方法进行了改进，使用图像中每一个像素点的模糊隶属度代替传统模型的灰度信息，构造模糊速度函数，将该函数替代传统轮廓模型中基于梯度信息的停止函数。

JV肺结节； 活动轮廓模型； 模糊速度； 模糊开运算； 水平集

0 引 言

肺癌是恶性肿瘤之一，且肺癌的发病率和死亡率持续升高。早期肺癌在CT影像上的表现形式为肺结节，及早发现肺结节对于癌症的诊断和治疗至关重要。肺结节分割是发现肺结节的重要基础，由于JV肺结节与血管之间具有相似的灰度值，并且存在亮度非均匀等特点，因此精确分割JV肺结节面临很多困难。

针对JV肺结节分割存在的难点，国内外众多学者提出许多算法。Chen[1]等将几何活动轮廓模型和C-V模型相结合，并提出了几何辅助的C-V模型；Krinidis[2]等为了加快活动轮廓曲线的收敛速度，在模型中引入了模糊隶属度；混合活动轮廓模型是将区域活动轮廓模型[3]和边界轮廓模型相结合，使得活动轮廓曲线收敛到目标对象的边界。但以上几种活动轮廓模型依然依赖梯度信息，导致发生边界泄露问题。文中首先根据刘乐[4]等肺实质分割算法来获取肺实质图像。

1 基于FVFACM的JV肺结节的分割

针对目前算法分割JV肺结节存在的边界泄露、收敛速度慢和分割精度低等问题，提出一种基于FVFACM的JV肺结节分割算法。算法流程如图1所示。

图1 算法流程图

1.1 构造形状-亮度指数结合的二维特征向量

由于待分割目标与背景区域具有较低的对比度，因此，仅仅通过亮度信息进行分割很难精确分割对象。所以，文中将图像的形状-亮度信息结合来进行图像分割。

传统形状指数通过该点的高斯曲率和均值曲率来获得，在理想状态下，肺结节区域的高斯曲率和均值曲率近似相等，血管区域的高斯曲率远大于均值曲率。但是在实际情况下， CT图像中掺杂着噪声，肺部组织的重叠致使肺结节区域和血管区域的形状指数不能明显地区分肺结节和血管。因此，文中结合Hessian矩阵将传统计算形状指数的两个曲率用Hessian矩阵中的两个特征值代替。结合后的形状指数定义如下：

(1)

式中：x----图像中的一点；

λ1、λ2----Hessian两个特征值。

肺结节图像及血管的亮度和形状指数如图2所示。

(a) 肺结节图像

(b) 肺结节的亮度值

(d) 肺结节的形状指数

(c) 血管的亮度值

(e) 血管的形状指数

图2 肺结节图像及血管的亮度和形状指数

图2(a)中左下箭头所指为血管区域，右上箭头所指为肺结节区域，图2(b)和(d)为肺结节区域的亮度值和形状指数，图2(c)和(e)为血管区域的亮度值和形状指数。

1.2 模糊隶属度的计算

采用模糊C均值来计算图像的模糊隶属度，假设图像共有n个像素点，并将图像划分为C个区域，每个区域的聚类中心表示为v={v1,v2,…,vc}。模糊聚类函数通过在算法迭代过程中寻找最合适的隶属度和聚类中心。其中，能量函数表示如下：

(2)

式中：uij----模糊隶属矩阵;

m----加权指数，通常情况下取m=2;

dij----第j个像素到第i个聚类中心之间的欧式距离,dij=‖xj-vi‖。

为了最小化能量函数，采用拉格朗日算法对其进行最小化求解，原能量函数可以等价为：

(3)

式中:λj----n个约束式的拉格朗日算子。

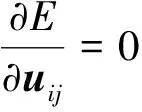
(4)

在约束条件的作用下，式(4)的算子可以表示为：

(5)

式中：k----第k个聚类区域。

因此，通过以下公式可求得能量函数的聚类中心和隶属度：

(6)

(7)

式中：t----迭代次数。

通过式(6)和式(7)不断迭代，寻找最优化的聚类中心以及隶属于本类的隶属度，当能量函数取得最小值时停止迭代，此时每个像素点都寻找到自己的类，并且隶属于本类的程度最大。

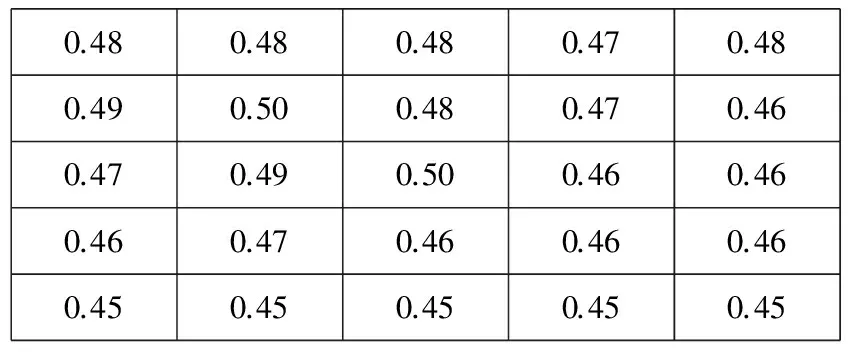
肺结节和血管的隶属度如图3所示。

(a) 肺结节图像

(b) 肺结节的模糊隶属度

(c) 血管的模糊隶属度

图3 肺结节和血管的隶属度

图3(b)和(c)分别为图3(a)中左下方箭头(血管区域)和右上方箭头(肺结节区域)所指区域的模糊隶属度。从表中可以看出,肺结节区域的模糊隶属度大于0.5，而血管区域的模糊隶属度小于0.5，因此,根据隶属度来进行模糊速度函数的构造，使得FVFACM模型能够充分利用图像的基本信息。

1.3 模糊速度函数

从上节的结论可知，血管和背景的模糊隶属度小于0.5，肺结节边界处的模糊隶属度接近0.5，而肺结节区域的模糊隶属度大于0.5，为此，若想实现活动轮廓模型在离目标对象较远时快速演变，在靠近目标对象的边界时减缓演变直至停止，模糊速度[5]函数V1(p)，V2(p)和V3(p)必须满足以下条件：

1)V1(p)，V2(p),V3(p)∈[0,1]；

2)当活动轮廓曲线处于目标对象边界时，V1(p)≈V2(p)≈V3(p)；

3)当活动轮廓曲线向目标对象边界靠近时，V1(p)，V2(p)和V3(p)逐渐减小。

所以，为了满足以上条件，将V1(p)，V2(p)和V3(p)定义为：

(8)

(9)

(10)

其中，t1，t2和t3都大于0，Z(p)是像素点p隶属于JV肺结节的模糊隶属度。

模糊速度和像素序号的对应关系如图4所示。

(a) 原始图像

从图4(b)可以看出，沿着虚线像素序号的模糊速度的变化情况，当模糊速度函数经过R点及S点时速度减小为0，当远离R点及S点时模糊速度逐渐增大，从图4(c)中可以看出，当模糊速度函数经过肺结节与血管相交的T点时模糊速度减小为0，当远离T点时模糊速度逐渐加快。通过图4(b)和(c)可以得出，当活动轮廓模型远离肺结节的边界时，通过模糊速度的变化来控制轮廓曲线加快像肺结节边界演化，有效地提高了算法的收敛速度，提高了效率。

1.4 基于FVFACM的活动轮廓模型

活动轮廓模型的思想是通过连续封闭的曲线来表达目标对象的边缘。首先，定义一个能量函数，并以事先定义好的一条封闭曲线作为这个能量函数的参数。当能量函数取得最小值时的轮廓曲线，即为目标对象的轮廓边缘。因此，分割过程就转变为求解能量泛函的最小值的过程。

假设图像上有一条闭环的轮廓曲线C，这条曲线将整个图像的区域分为内、外两部分，内部用Ω1来表示，外部用Ω2来表示。将以这条曲线作为参数的轮廓模型的能量函数[6]定义为：

(11)

式中: L(C)----曲线的长度;

p----某一像素点，p∈Ω;

I(p)----某一个像素点的亮度值;

c1、c2----分别表示图像内部和外部的平均亮度值;

V1(p)----活动轮廓曲线在像素点p向内的速度函数;

V2(p)----活动轮廓曲线在像素点p向外的速度函数；

V3(p)----轮廓边界处的速度函数。

该算法利用水平集函数来引导活动轮廓曲线进行演变。假设在活动轮廓曲线C外部水平集函数φ取值小于零，在曲线C内部水平集函数φ取值大于零。活动轮廓模型的模糊速度函数的水平集[7]定义如下：

(12)

式中: c1----轮廓曲线内部的平均亮度值;

c2----轮廓曲线外部的平均亮度值。

基于欧拉-拉格朗日变分法[8]，采用标准梯度下降法来对活动轮廓模型的能量函数进行最小化，经过变分后的能量函数为：

(13)

式中：δ(φ)----Dirac函数，即Heaviside函数的导数。

将式(8)～式(10)代入式(13)可知，当活动轮廓曲线向目标对象边界演化时，模糊速度函数V1(p)，V2(p)和V3(p)逐渐减小，活动轮廓曲线演化的速度也随着模糊速度函数的不断减小而减小，当活动轮廓曲线接近目标对象的边界，此时，模糊速度函数较小,甚至到零，活动轮廓曲线停止演变，分割结束。

2 实验结果与分析

采用吉林省某医院提供的数据作为实验数据。实验数据集见表1。

表1 实验数据集

实验中，模糊控制常数m取3.0，模糊形态学开运算使用模板大小为5×5，计算模糊速度函数的正常数t1，t2和t3分别为2。

使用几种不同的分割方法进行JV肺结节分割的结果如图4所示。

(a) 边界模型 (b) 区域模型 (c) 混合模型 (d) 文中模型

图5 JV肺结节的分割结果

从图5(a)、(b)、(c)中可以看出,无论是采用区域活动轮廓模型、边界活动轮廓模型还是混合活动轮廓模型进行分割都存在边界泄露的问题;从图(d)可以看出,使用文中模型的分割结果相对于其他模型更好，有效解决了边界泄露的问题。

分割错误率见表2。

表2 分割错误率(60个JV肺结节)

表2是对表1中的实验数据集分别使用已有模型和文中模型所得到的分割错误率A(Cm,C0),定义[9]为：

(14)

式中:Cm、C0----分别为提取和期望提取的肺结节的边界。

3 结 语

充分利用图像的基本信息，通过利用图像的灰度信息和形状特征构造基于灰度和形状的二维向量，并通过模糊C均值聚类算法来求取图像的模糊隶属度，进而构造模糊速度函数，将模糊速度替代传统模型的基于梯度的边界停止函数，通过引入模糊速度函数有效地解决了边界泄露、收敛速度慢等问题，并提高了分割的精度，因此，文中提出算法较传统的基于边界的活动轮廓模型和基于区域的活动轮廓模型等均可以提高分割精度。

[1]ChenL,ZhouY,WangY,etal.GACV:Geodesic-AidedC-Vmethod[J].PatternRecognition,2006,39(7):1391-1395.

[2] Krinidis S, Chatzis V. Fuzzy energy-based active contours[J]. IEEE Transactions on Image Processing A Publication of the IEEE Signal Processing Society,2009,18(12):2747-2755.

[3] 林喜兰,陈秀宏,肖林云.基于区域混合活动轮廓模型的医学图像分割[J].计算机科学,2016,43(4):303-307.

[4] 刘乐,李阳,侯阿临,等.基于CT图像的肺实质分割[J].长春工业大学学报,2015,36(1):72-76.

[5] 黑啸吉,蒋慧琴,马岭,等.一种基于低剂量CT图像的肺结节分割方法[J].计算机应用研究,2017(1):290-294.

[6] 陈侃,李彬,田联房.基于模糊速度函数的活动轮廓模型的肺结节分割[J].自动化学报,2013,39(8):1257-1264.

[7] Zhang K, Song H, Zhang L. Active contours driven by local image fitting energy[J]. Pattern Recognition,2010,43(4):1199-1206.

[8] Li C, Kao C Y, Gore J C, et al. Minimization of region-scalable fitting energy for image segmentation[J]. IEEE Transactions on Image Processing A Publication of the IEEE Signal Processing Society,2008,17(10):1940-1949.

[9] Ying Z, Guang yao L, Xiehua S, et al. Geometric active contours without re-initialization for image segmentation[J]. Pattern Recognition,2009,42(9):1970-1976.

JV type pulmonary nodules segmentation based on FVFACM

LIU Liwei， WANG Guoming*

(School of Computer Science & Engineering, Changchun University of Technology, Changchun 130012, China)

To improve traditional methods of active contour model segmentation for pulmonary nodules, we replace gray levels of a traditional model with fuzzy membership degree of every pixel of an image, and the gradient-based cease function in a traditional contour with fuzzy velocity function.

JV pulmonary nodules; active contour model; fuzzy speed; fuzzy open operation; level set.

2016-12-19

吉林省教育厅科研专项项目(2014142)

刘丽伟(1974-)，女，汉族，吉林通化人，长春工业大学副教授，博士，主要从事模式识别与嵌入式系统方向研究,E-mail:liuliwei@ccut.edu.cn. *通讯作者：王国明(1990-)，男，汉族，吉林松原人，长春工业大学硕士研究生，主要从事图像处理方向研究,E-mail:987292012@qq.com.

10.15923/j.cnki.cn22-1382/t.2017.3.11

TP 391

A

1674-1374(2017)03-0270-06