大型复杂锻铸件三维扫描点云数据去噪及光顺研究
郑 鹏,霍洪旭,姜兴宇
(沈阳工业大学 机械工程系,辽宁 沈阳 110870)
大型复杂锻铸件三维扫描点云数据去噪及光顺研究
郑 鹏,霍洪旭,姜兴宇
(沈阳工业大学 机械工程系,辽宁 沈阳 110870)
逆向工程,对锻铸件的三维点云数据处理是获得复杂零件外形尺寸的关键环节。如何从散乱的、多噪点的点云数据中得到无噪点、光滑的三维点云是人们一直研究的重点。依据散乱点云中的噪声点的特征进行分类,并提出一种分步去噪及光顺方法。首先用格网阀值法去除第一类噪点,用格网法去除第二类噪点,最后用双边滤波法对数据进行光顺处理。结果表明该方法不仅有效去除了锻铸件的三维点云数据的噪声点,同时获得了光滑的测量表面,保留了尖锐特征。
三维激光扫描;数据处理;数据滤波;去噪;光顺;锻铸件
0 前言
三维测量方法可分成接触式与非接触式两类。接触式基于力触发原理测量三维数据,典型设备是三坐标测量仪(CMM)。大型复杂锻铸件由于表面粗糙,结构复杂,对其测量以非接触式为主。非接触式测量是基于光学、声学和电磁学原理[1],通过算法将物理模拟量转化为三维点云。在采集锻铸件的点云数据时,由于测量仪器本身的缺陷和人为干扰等原因,在采集到的点云数据点中往往含有大量噪声点。为了保证测量精度,同时又能保证形貌数据完整,必须先对原始点云数据进行去噪和光顺处理。然而对锻铸件的三维点云数据处理的研究相对滞后,点云数据去噪和光顺一直是人们研究的重点。
许多学者已经在去噪、光顺方面做出了一些研究。刘辉等人将最小二乘法用于轮廓内的连续错误噪点的数据滤波,提出一种对双向去噪方法[2]。王丽辉等人将鲁棒的模糊C均值算法用于去除大噪点,提出一种鲁棒算法和点云双边滤波结合去噪方法[3]。梁新合等人将光顺后的结果作为补偿量,提出一种补偿滤波算法[4]。宋阳等人引入模糊聚类权重因子,提出一种改进C均值算法[5]去除大尺寸噪点。通过分析发现几乎每一种算法都有一定的局限性,有待进一步的改进。
在MATLAB环境下获取点云数据,并完成数据重构,并根据MATLAB的环境中点云数据特点,对噪点进行分类去噪光顺。本文根据点云数据特征类型,将其分成四类,第一类数据点是偏离真实样件数据点较远的、数量较少的离散稀疏噪点。第二类是偏离真实样件数据点较远的、数量较多的密集噪点。第三类是由于设备原因在真实样件的数据点中穿插的不易处理的噪点。第四类数据点是样件理想状态下的数据点。针对上述问题,本文提出一种结合格网阀值法和三维双边滤波方法的点云数据去噪及光顺算法。这样处理的优点在于既可以解决原始点云数据中包含的孤立点云,也避免产生过光顺的问题。
本文对大型复杂锻造件进行数据处理实验,证明该方法与传统的单一形式去噪方法相比,不但高效去除点云数据的噪声点、完成数据光顺,同时还保留了样件的基本特征。
1 第一类噪点去除算法
第一类噪点为悬浮在样件数据上空,并散乱稀疏的分布在四周,如图1所示。同时也是很明显的错误点,必须在光顺前去除。本文采用格网阀值法,通过划分网格,求其数据点的数量与预先设定的阀值对比,如果数量小于阀值,则将该网格内的所有点从原始数据点中删除。这样做的目的是删除第一类噪点,也叫孤点。具体方法如下:
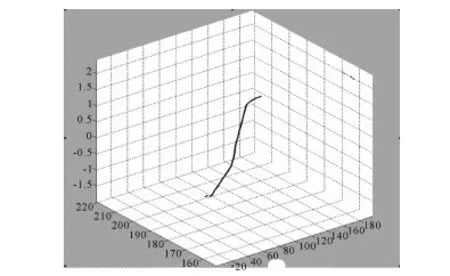
图1 某测量实验的三维点云原始数据
1.1 构建虚拟包围盒
首先,读取原始点云数据,并将点云三维坐标存储在一维数组中,获取所有数据点的位置极值坐标,模拟出一个平行于坐标系的长方形包围盒,因此包围盒内包含所有原始数据点,并根据公式(1)将其分割成若干个边长为L的小立方体[6]。
(1)
式中,h为网格比例因子,取值范围在1.0~1.5之间;N为全部点云数量。
设虚拟包围盒的最小坐标(xmin,ymin,zmin)和最大坐标(xmax,ymax,zmax)。其中,小立方体的在三个方向的个数分别为
(2)
(3)
(4)
1.2 判断小立方体的点云数据
在三维点云数据和它的编号之间构建一个确定的并与之对应的哈希函数,使每个编号与唯一的小立方体相对应。假设原始数据点云的任意一点P的坐标为(Px,Py,Pz),则
(5)
(6)
(7)
其中,I,J,K分别是该点对应的小立方体的编号。散乱点云格网化后,将对三维空间中悬浮在样本点之外的、散乱稀疏的噪点剔除,采用的方法是判断每个小立方体中的数据点个数,如果数量小于规定的阀值,则清空此立方体的数据。
实验中,将某点云数据导入到MATLAB中显示,如图1所示。由于外界原因,激光扫描仪将噪点保留,通过格网阀值法将点云数据的偏离样本点较远的数据点剔除,剔除后的结果如图2所示。

图2 用格网法去除第一类噪点效果
2 第二类噪点去除算法
在第一类划分网格的基础上,按顺序搜索点云数据中小立方体是否有数据点,如果有数据点个数不为零,则以此立方体为中心,搜索周围立方体中包含数据点的立方体。如果存在这样立方体再依次以周围立方体为中心,搜索其周围立方体,直到所有立方体被查看完。找出属于同一相邻立方体并存在数据点的点云,通过对比不同点云的数据点个数,保留最多的点云,剔除距离大片点云较远的密集点云,即第二类噪点。图3为用格网法去除第二类噪点效果。
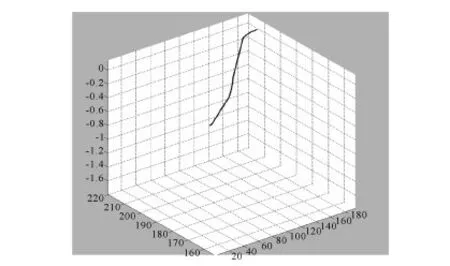
图3 用格网法去除第二类噪点效果
3 第三类噪点光顺算法
本文将双边滤波算法引进到三维光顺点云数据当中,以此来光顺第三类噪点。
3.1 图像中的双边滤波算法
双边滤波算法(BLT)首先应用在滤除二维图像噪声点,Fleishman等人用周围点灰度值的加权平均来代替当前点的灰度值[7],该方法简单有效并且在保持图形的基本特征的同时,达到光顺目的。
二维图像的双边滤波算法[8]的基本公式为
(8)
式中,q为像素点,N(q)为q的相邻像素集合;k是q的相邻像素点;(║q-k║)是像素q与相邻的像素k之间几何距离;L(q)为像素q的灰度值;(|L(q)-L(k)|)是像素q与相邻的像素k之间灰度的相似性;Wc和Ws都是高斯函数。
3.2 三维点云样件的双边滤波算法
三维双边滤波方法用于光顺三维点云数据,以此来光顺点云数据中小尺度的噪点。重新定义
q∶=q+an
(9)
式中,q为原始数据点;q:为光顺后的数据点;n是q的法失方向;a是双边滤波权因子,定义为
(10)
(11)
(12)
式中,Wc类似于二维图像中的双边滤波权函数,称为空间域(距离)权重;Ws为用来捕捉领域点之间的法向的变化,称为特征域权重或影响权重[9];c和s为切平面上的高斯核函数的滤波系数,分别代表了某一点的双边滤波函数值的切向量和方向量的影响范围。其中,c为原始数据点q到领域点的距离对该点的影响因子,s为原始数据q到领域点的距离向量在该点法失方向上的投影对于原始数据点的影响因子。c为点领域半径,不同的s的取值影响最终的光顺效果,常见的s为邻域点的标准偏差。σs为空域高斯函数的标准差,σr为值域高斯函数的标准差。
3.3 双边滤波算法及光顺步骤
(1)任意数据点qi的m个相邻点kij,j=1,2,3,…,m;
(2)求出相邻点的光顺滤波函数的几何距离║qi-kij║,即数据点qi到相邻点kij的几何距离;
(3)求出保持权重函数的内积参数
(4)依据距离权重和特征域权重公式计算出双边滤波函数;
(5)将(4)中的Wc和Ws代入双边滤波权因子公式,求出C;
(6)用新数据点替代原始数据点 ;
(7)循环完成所有数据点的更新,保存结果,程序结束。
三维双边滤波函数的几何距离及Wc和Ws的MTALAB计算算法:
y(j)=dot(normal(i,:),points(i,:)-points(indx(i,j),:));
wc(j)=exp(-(dist(i,j)^2)/(2*mc^2));
ws(j)=exp(-y(j)^2/(2*ms^2));
d1(i)=d1(i)+wc(j)*ws(j)*y(j);
d2(i)=d2(i)+wc(j)*ws(j);
4 算法的实现过程
(1)首先通过对原始的点云数据的预处理进行极大极小点云的剔除,缩小去噪的运算时间。
(2)在XOY平面坐标系内,找出X坐标和Y坐标的极值点,然后模拟出一个平行于坐标系的长方形包围盒,判断其格网点云数量,对少于阀值的格网进行清空,完成第一类噪点的去噪。
(3)利用区域增长思想[10],搜索三维点云中每个小立方体是否存在数据点,如果某个立方体有数据点,并以此为中心继续搜索,直到网格都被搜索。再判断网格是否相邻,找出相邻点云的最大点云数量。除去其他点云,完成第二类噪点的去噪。
(4)改进二维图形双边滤波器,运用三维双边滤波原理去光顺(3)中的噪点数据。完成第三类噪点的去噪。
5 实验分析与评定
5.1 实验数据
为验证本文算法的效果,用手持三维激光扫描仪对某铁矿测量件进行三维数据测量实验,获取锻铸件的原始点云数据,如图4所示。其设备分辨率为0.4mm×0.5mm×0.4mm,获得约220 332个高密度数据点。数据处理实验在Matlab2014环境下进行,新建硬件平台为280 Hz处理器、512 MB内存。

图4 手持3D扫描仪获取锻铸件原始点云数据
考虑到目前某软件应用较为广泛[11],将本文算法输出结果与其进行比较。其应用原理是用许多细小的空间三角形来逼近还原CAD实体模型,采用NURBS曲面片拟合出NURBS曲面模型。
5.2 实验结果分析
根据上述方法对点云数据进行分析,达到了预期效果。其中,图5为没有处理的原始点云数据和某软件数据处理效果。图6为应用MATLAB采用本文算法滤波效果。图7、图8为原始点云重建结果和光顺后的点云重建结果。

图5 数据滤波前后三维效果图
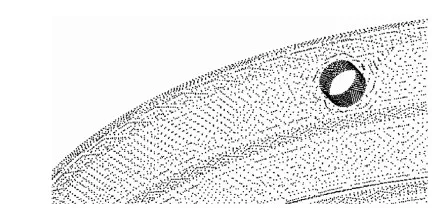
图6 应用MATLAB采用本文算法滤波效果

图7 原始点云重建结果
图8 光顺后点云重建结果
5.3 评定标准
对于去噪光顺算法的评定是一个新的研究方向,在数据处理中扮演重要角色,是检验方法可行性的重要条件。目前,去噪光顺算法的评定主要有目视检查法、随机抽样检查法[12]、定性评价[13]、交叉表分析法、Kappa系数法和平均二次距离误差法。
(1)交叉表分析法[14]。交叉表(交叉列联表)分析法是一种以表格的形式同时描述两个或多个变量的联合分布及其结果的统计分析方法。基于表1的评价系统,按照Ⅰ类误差、Ⅱ类误差和总误差进行定量分析。具体如下:
Ⅰ类误差是指样件点错分为非样件点的概率,用b/a表示;
Ⅱ类误差是指非样件点错分为样件点的概率,用c/f表示;
总误差是指分类结果与参考数据不一致的概率,用(b+c)/n表示。

表1 交叉表
其中,a表示算法正确分类的样本点个数,b表示样本点误判为非样本点的个数,c表示非样本点误判为样本点的个数,d表示算法正确的分类的非样本点个数,e和f分别表示参考数据中样本点和非样本点个数;g和h分别表示去噪光顺结果中样本点和非样本点个数。
在实际情况下,零件的表面情况比较复杂,通常通过调整实验参数,对比实验结果,选择较小的Ⅰ类误差。总误差是衡量Ⅰ类误差和Ⅱ类误差错误总数的标准,所以通过对比总误差,选择较为合适的数据。统计处理前后的去噪指标如表2所示,本文方法的Ⅰ类误差相对Ⅱ类误差较大,说明在数据滤波时,要尽可能保证样件结构特征、保证点云数据数量的同时,也要达到去除噪点和光顺的目的。

表2 交叉表分析法分析实验数据结果
(2)Kappa系数法。kappa系数[15-16]是一种检查分类评价一致性的计算精度方法。它是通过把所有地表真实分类中的像元总数乘以混淆矩阵对角线的和,再减去某一类地表真实像元总数与被误分成该类像元总数之积对所有类别求和的结果,再除以总像元数的平方差减去某一类中地表真实像元总数与该类中被分类像元总数之积对所有类别求和的结果所得到的。Kappa系数与分类结果和参考数据的吻合度成正比。Kappa系数定义如下:
(13)
计算得到Kappa=0.94,表明实验方法得出的分类结果与参考数据紧密吻合。

(14)
此方法适用于多次迭代双边滤波器,在分析Bunny等模型双边滤波时,可以体现多次迭代双边滤波收敛特性,但多次迭代对于不同的锻铸件可能造成过于光顺现象。
6 结束语
本文提出一种格网阀值法和双边滤波器相结合的分类去噪方法,通过实验验证了该方法的有效性,得出结论。
(1)在原始点云光顺之前,采用格网法有效的去除噪点,为后续光顺处理奠定基础,有效保证数据的完整性。
(2)对实验数据应用本文算法和某商业软件进行对比实验,结果证明本文的算法能够很好的去除噪点的同时,还能保证数据样点的结构特征。
(3)对去噪效果评价的指标进行汇总,对实验结果进行定量的评价,结果显示评价指标在允许误差范围内,说明算法已经达到预期的效果。
[1] 赵灿,董刚,程俊廷.利用噪声特点与曲面拟合的点云去噪及光顺算法研究[J].现代制造工程,2008(06):90-93.
[2] 刘辉,王伯雄,任怀艺等.基于三维重建数据的双向点云去噪方法研究[J].电子测量与仪器学报,2013,27(01):1-7.
[3] 王丽辉,袁保宗.鲁棒的模糊C均值和点云双边滤波去噪[J].北京交通大学学报,2008,32(02):18-21.
[4] 梁新合,新晋,郭成, 等.散乱点云的补偿滤波[J].西安交通大学学报,2011,45(11):91-95.
[5] 宋阳,李昌华,马宗方,等.应用于三维点云数据去噪的改进C均值算法[J].计算机工程与应用,2015,51(12):1-4.
[6] LES APIEGI,WAYNE THLLER.Algorithm for Finding All k Nearest Neighbors [J].Computer-Aided Design,2002,34:167-172.
[7] Fleishman S,Drori I,Cohen-Or D.Bilateral mesh denoising [J].ACM Transcations on Graphics,2003,22(03):950-953.
[8] JIN Ming , SONG Jian-zhong.An adaptive bilateral filtering method for image processing [D]. Opto-Electronic Engineering,2004,31(07):65-68.
[9] 杜小燕,姜晓峰,郝传刚, 等.点云模型的双边滤波去噪算法[J].计算机应用与软件,2010,27(07):245-247.
[10]曹爽,岳建平,马文.基于特征选择的双边滤波点云去噪算法[J].东南大学学报,2013,43(02):351-354.
[11]TU QUN-ZHANG ZHAO JIAN-XUN DAI JV-YING. A Method of Reverse Modeling of Equipment Parts by Combining Geomagic Studio and Pro/Engineer [J]. 2011 International Conference on Computer Science and Logistics Engineering,ZhengZhou, 2011:366-370.
[12]周骏,陈雷霆,刘启和, 等. 基于序贯概率及局部优化随机抽样一致性算法[J].仪器仪表学报,2012,33(09):2037-2044.
[13]高志国.海量点云数据滤波处理方法研究[J].测绘工程,2013,22(01):35-38.
[14]胡永杰,程朋根,陈晓勇, 等.机载激光雷达点云滤波算法分析与比较[J].测绘科学技术学报,2015,32(01):72-77.
[15]MENG,WANG,SILVAN-CARDENAS,et al.A Multi Dir-ectional Ground Filtering Algorithm for Airborne Li-DAR[J]. Photogrammertric Engineering and Remote Sensing,2009,64(01):117-124.
[16]SHAO YICHEN,CHEN LIANGCHIEN.Automated Sea-rching of Ground Points From Airborne LiDAR Data Using a Climbing and Sliding Method [J].Photogra-mmertric and Remote Sensing,2008,74(05):625-635.
Study on denoising and smoothing method of 3D-scaning point cloud data tothe large complex malleable cast parts
ZHENG Peng, HUO Hong-xu, JIANG Xing-yu
(Mechanical Engineering Department,Shenyang University of Technology,Shenyang 110870, China)
Reverse engineering is the key part to obtain dimensions of complex parts for the processing of three-dimensional point cloud data of malleable cast parts. The key point is how to get the noiseless and smooth 3D point cloud from the scattered and multi-noise point cloud data. According to characteristics of noise points in the scattered cloud, this paper presents two methods: step-by-step denoising and smoothing method. First, the first kind of noise is removed by using grid threshold method. Second, the second kind of noise is removed by using virtual grid method. Finally, the above data is smoothed by using bilateral filtering method. The results show that the method not only removes the noisy points of 3D point cloud data, but also obtains a smooth measurement of surface and retains the characteristics of sharp features.
3D laser scanning; data processing; data filtering; denoising; smoothing; malleable cast parts
2016-10-09;
2016-12-18
国家自然科学基金项目(NO.51305279)
郑鹏(1964-),男,教授,主要研究方向为现代制造技术与测量、数控制造技术、机械成套设备设计与开发。
霍洪旭(1990-),男,硕士生,主要研究方向为三维扫描测量与三维建模。
P204
A
1001-196X(2017)03-0023-06

