基于NSGA-II的多目标航班机型分配问题研究

樊 玮，别好杰

（中国民航大学计算机科学与技术学院，天津 300300）

基于NSGA-II的多目标航班机型分配问题研究

樊 玮，别好杰

（中国民航大学计算机科学与技术学院，天津 300300）

机型分配是航空公司运营管理中资源优化的重要难题之一，在很大程度上影响着航空公司的利润率及竞争力。针对现有机型分配方法中求解目标的单一性，在基本机型分配模型的基础上建立了多目标机型分配模型，即同时将最大化航空公司利润和使用最少的飞机架数覆盖全部航班作为目标。对于多目标数学模型求解的复杂性，采用了NSGA-II算法，以避免求解时的目标偏好性。通过算例对此模型求解，验证了模型的有效性，对比单目标机型分配模型，结果表明多目标机型分配模型在目标空间上分布更均匀，能够为航空公司航班机型分配提供决策支持。

航空运输；机型分配；NSGA-II算法；多目标优化；航班

机型分配问题是指根据不同机型的不同座位数、运营成本和潜在收益，分配不同的机型给各定期航班。近年来，随着航空运输业的高速发展，航空公司的竞争逐步加剧，航线网络与资源优化已成为航空公司提高竞争力的有效手段，而机型分配是航线网络与资源优化的关键方法之一。

目前，有关机型分配的国内外研究主要包括：Abara[1]在连接网络法的基础上建立了机型分配模型，该模型以最大化航空公司利润为目标；Brown[2]主要侧重于对枢纽轮辐式航空公司机队规划的研究，通过构建基于面板数据的模型分析了航空管制因素对其机队构成的影响，只考虑了放松航空管制后各机型飞机架数在航线上的限制；Hane等[3]构建了一种基于时间拓展网络的多商品流模型，用于解决机型分配的大规模整数规划问题，在模型求解中用到了内点算法，并通过数据验证了该模型和算法在解决大规模整数规划问题上的优越性，但此算法的时间复杂度较高；Listes等[4]通过情境聚合算法求解基于时空网络的机型分配模型，模型考虑到了乘客的动态需求，最后通过实际数据验证了模型和算法的可行性和优越性；Barnhart等[5]在基本机型分配模型（FAM）和基于行程的机型分配模型（IFAM）的基础上，提出了一种通用机型分配模型（GFAM，generic fleet assignment model），该模型以航空公司利润最大化为目标；Shao等[6]综合考虑了机型分配与航班计划中飞机排班和机组排班，并以这3个阶段建立一个数学模型，通过Benders分解法求解；徐进[7]构建了一种混合整数规划的机型指派模型，并对时间窗口的机型指派问题做了初步分析研究；乐美龙等[8]提出了一种基于时空网络的航班机型分配模型，该模型以最小化航班机型分配总成本为目标函数；Liu等[9]在考虑延迟传播的情况下，结合机型分配和飞机路径建立了单目标数学模型。

以上研究虽然考虑的影响因素和优化方法有所差异，但其基本约束条件（航班覆盖、飞机平衡、机队规模）基本相同，且目标函数都集中在利润最大化或最小化运营成本其中一个单一目标上，考虑到航空公司实际需求，本文同时将最大化航空公司利润和使用最少的飞机架数覆盖全部航班作为目标，在基本机型分配模型[10-12]的基础上建立了多目标机型分配模型，即将机队规模加入了目标函数中，考虑的重点约束条件包括航班覆盖、飞机平衡、飞机利用率等。Pareto最优解是多目标优化求解的主要方法[13]，很难用传统方法求解，为此，本文引入了计算方便、设计性强的带精英策略的快速非支配排序遗传算法NSGA-II[14-15]。对航空公司而言，通过求解此模型得到的机型分配方案，对提高各机型飞机使用效率、降低经营成本、获得更高的收益有着十分重要的意义。

1 多目标航班机型分配模型

1.1 时空网络法

用数学模型表示机型分配问题的一个主要难点在于如何跟踪不同机场、不同时间机队的情况，时空网络图可以很容易解决这个问题。图1包含3个机场、2种机型，8个航班（1~8）、14个节点（A~O）时空网络。

在时空网络图中，纵轴代表时间，横轴代表机场。图1中，连线（箭头）表示航班段，节点表示某个机场在一天中某个特定时间航班的进出港情况；折线（带箭头）表示地面连接线，用于将机场的最后一个到达节点与第一个始发节点连接起来，这种线表示飞机在该机场过夜，它将某一天的最后一个进港航班与第二天的出港航班衔接起来。所以，时空网络图可以很好地解释机型分配模型中约束条件飞机平衡这一概念，即某节点停在地面上的某个机型的飞机架数=该节点之前地面上同机型飞机的架数+到达该节点同机型飞机的架数-飞离该节点同机型飞机的架数。如在机场1，节点B处机型738的飞机架数=节点B处机型738 的飞机架数+1（航班 2）-1（航班 3）。

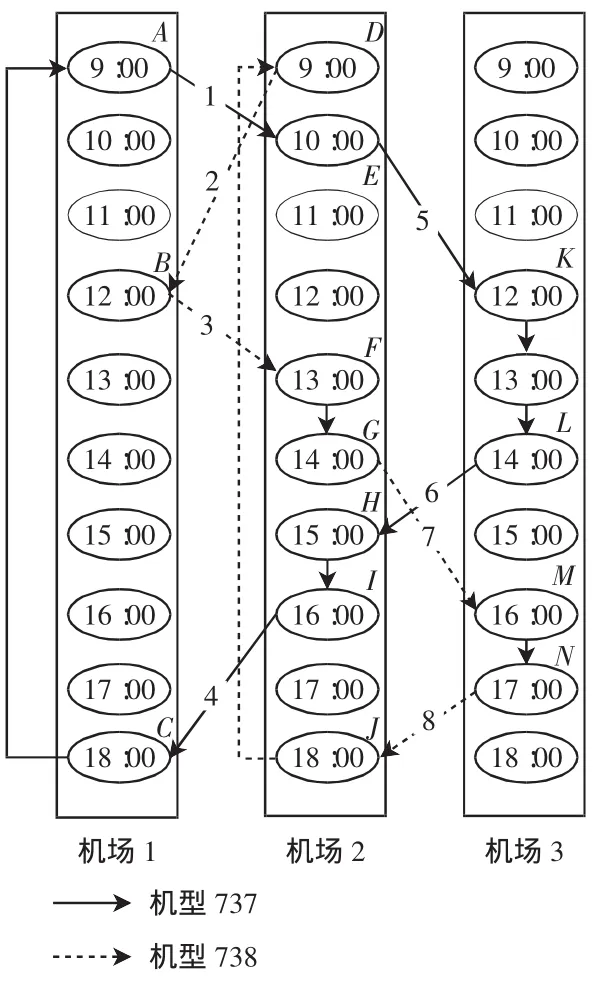
图1 时空网络图Fig.1 Time-space network diagram

1.2 多目标机型分配的数学模型

以最大化航空公司利润和使用最少的飞机架数覆盖全部航班作为目标，在已知航班时刻表（包括航班号、起飞时间、到达时间、始发机场、到达机场、飞行时间、航程、平均票价）、乘客需求、机队结构的基础上，首先通过时空网络法构建航班网络，然后在航班网络的基础上建立了同时优化航空公司利润和覆盖全部航班飞机架数的多目标机型分配模型。

1）集合

模型所包含的集合有：F表示航班集合；H表示经停航班集合，H⊂F；J表示机型集合；O表示机场集合；M表示时空网络中所有节点的集合；E表示时空网络中终止节点集合，E⊆M。

2）下标变量

模型所含的下标变量有：i表示航班，i∈F；j表示机型，j∈J；o表示机场，o∈O；m表示时空网络中的节点，m∈M；e表示时空网络中的终止节点，e∈E；h表示一个经停航班，h∈H，针对实际情况只考虑一次经停，每个经停航班h将整个航程分成h1和h2两个航段。

3）参数

模型所涉及的参数有：ti表示航班i的飞行时间；Lj表示机型j最大日利用率；spill表示乘客的溢出率；Nj表示机型j数量；i.pax表示航班i的乘客需求；Sj表示机型j的座位数；Gm，j表示在节点m处机型j的架数。

4）决策变量

模型涉及的决策变量有：am，i=1，表示在节点m处航班i为进港航班；am，i=-1，表示在节点m处为出港航班；Xi，j表示决策变量，当机型j分配给航班i时取值1，否则为0。

5）模型

其中：f1为每个航班分配一种机型后航空公司总的利润（取反）；f2为每个航班分配一种机型后使用总的飞机架数；Pi，j表示机型 j执行航班 i的收益；Ci，j表示机型j执飞航班i时的总成本；Ge，j表示在时空网络中终止节点e处机型j的飞机架数。计算如下

约束条件：式（2）为航班覆盖，确保每一个航班分配一种机型；式（3）~式（4）为飞机平衡或设备的连续性，保证了在需要的地方及需要的时间里会从正确的机型中提供1架飞机；式（5）为飞机利用率约束；式（6）为飞机座位数约束，即如果航班i的乘客量i.pax=100，最大旅客溢出量spill=0.1，则要求分配给航班i的机型座位数Sj≥90；式（7）表示经停航班约束，即要求一次经停航班的两个航段分配相同的机型；式（8）表示Xi，j为 0-1 决策变量。

2 模型求解

2.1 NSGA-II算法基本原理

NSGA-II算法是一种基于进化算法（EA）的多目标优化（MOO）方法之一，由Srinivas和Deb于2000年提出的。在遗传算法（GA）的基础上，NSGA-II算法提出了3种关键技术（快速非支配排序、拥挤度和拥挤度比较与精英策略）：①非支配排序算法保留了最优秀的解决方案，其作用是指引搜索向Pareto最优解集方向进行；②采用拥挤度与拥挤度算子以保持解决方案的多样性；③精英策略为了保留父代中的优良个体直接进入子代，以防止获得的Pareto最优解丢失，个体的优良由目标函数决定。而NSGA-II算法中的选择、交叉与变异算子和遗传算法中这3个算子的原理相同。NSGA-II算法能够找到使各目标函数能尽量达到比较大（或比较小）的Pareto最优解集，为各目标函数之间权衡提供了有效的工具。算法的基本原理如图2所示。

图2NSGA-II原理图Fig.2 Principle of NSGA-II diagram

其中：Pt表示在t代产生的种群，种群大小为N；Qt表示在父代种群Pt上通过遗传操作产生的子代种群；Rt表示Pt与Qt合并组成的种群，种群大小为2N；Z1，Z2，Z3…表示在种群Rt上通过非支配排序算子产生的非支配集；Rt+1表示在Rt的基础上，通过上述3种技术产生的第t+1代种群，种群大小为N，种群Pt的产生过程与此一样，种群Qt+1的产生过程与Qt一样。

2.2 模型求解的步骤

本文将NSGA-II算法应用于式（1）所示模型求解，具体算法实现如下：

1）输入输出

输入：机型集合J，航班集合F；

输出：最优的航班机型对。

2）程序流程

初始化种群：

For pop：随机生成1组染色体

While染色体不满足约束条件

重新生成；

End while

End for

计算染色体适应度，即目标函数值；

初始化种群排序；

For Gen：

锦标赛选择；

交叉和变异操作：

While染色体不满足约束条件

重新进行交叉或变异操作；

End while

计算染色体适应度，即目标函数值；

非支配排序和拥挤度排序；

替代种群，即生成子代；

End for

3 算例

该算例涉及40个航班，80个结点，19个机场，航班时刻表，如表1所示。其中，各航班段最大旅客溢出量均取0.1，航班段旅客量由历史数据预估得出，机票价格由航线市场年总收入除以实际运输旅客量，计算得到平均票价。

假设航空公司40个航班可使用的机型有737和738两种，每种机型的座位数、日最大利用率、座公里成本费用，如表2所示。

表1 航班时刻表Tab.1 Flight timetable

表2 各机型数据表Tab.2 Data of aircraft type

3.1 模型的求解过程

本文实验的目的是为该航空公司的40个航班分配机型，使得航空公司的40个航班获得的总利润最大和覆盖这40个航班所用的飞机架数最少，从而验证模型的可行性和有效性。

1）计算每种机型下航班的利润

其中：i.price表示航班i的平均票价；i.pax≤Sj表示航班i的乘客量小于等于机型j的座位数，没有乘客溢出；i.pax>Sj表示航班i的乘客量大于等于机型j的座位数，有乘客溢出。

航班分配成本计算，包括两部分：运营成本OCi，j和溢出成本 SCi，j，即

其中：CASMj为机型j的座公里成本[6]；di为航班i的航程；溢出成本 SCi，j可表示为

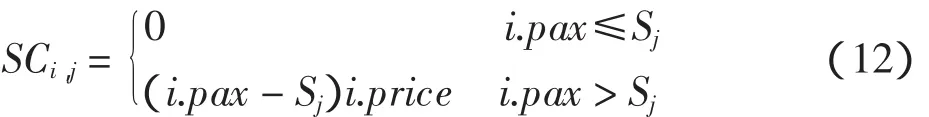
2）采用NSGA-II算法为航班分配机型，算法设计如2.2节。其中交叉概率Pc和变异概率Pm根据生成的随机数取值，若生成的随机数小于0.9，则进行交叉操作，否则进行变异操作。设置参数种群规模pop及最大进化代数Gen并进行实验。

3.2 实验结果及分析

通过以上方法，求得的Pareto最优解集，即航班机型分配方案如表3所示。Pareto前沿，即与表3中方案对应的目标函数值如表4所示。

为了验证所提模型的有效性，在同样的条件下，建立仅以航班总利润最大为优化目标，不考虑使用最少的飞机架数覆盖全部航班的单目标机型分配模型，对这40个航班分配机型，得到的结果与方案2相同。对比两个方案的目标函数，可知方案1和方案2在两个目标函数上具有互不支配的特点，同属Pareto最优解。方案1在使用的飞机架数上占优，方案2在航班总利润上占优，而方案1的飞机利用率明显占优。对比单目标机型分配模型，说明了基于NSGA-II算法的多目标机型分配获得的解集在各目标空间上分布更为均匀，更具多样性，能够为航空公司航班机型分配提供更多选择空间。

表3 航班机型分配方案Tab.3 Airline fleet assignment scheme

表4 机型分配方案Tab.4 Fleet assignment scheme

表5给出了这4个机场各机型需要的过夜飞机架数，其余15个机场过夜飞机架数都为0。

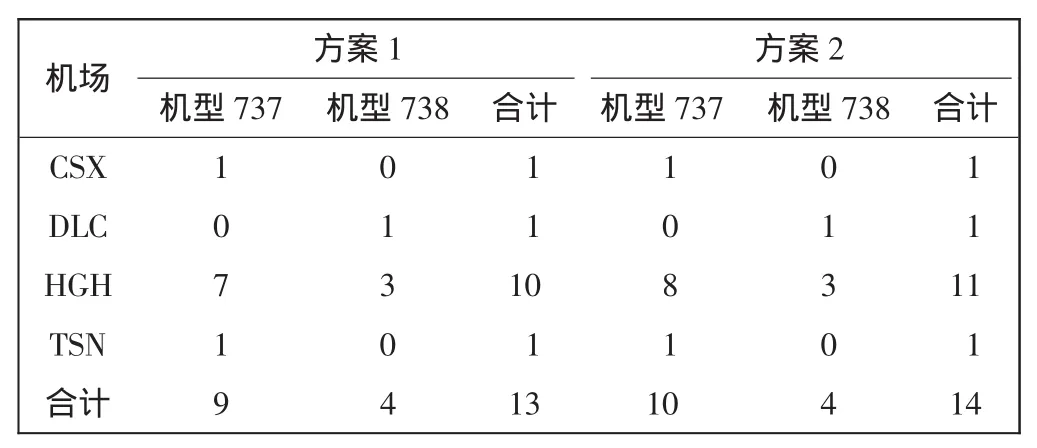
表5 各机场各机型飞机分布Tab.5 Aircraft distribution of airports

通过计算得出各机型的日平均利用率如表4所示，而通常情况下737机型和738机型的日平均利用率分别约为8.28 h和7.2 h。此时，航空公司需求的总飞机数量为13或14架，为了获得更好的机队配置组合，可以通过调整机队的机型配置获得总利润和日利用率较高的配置方案。表6为部分配置方案，从表中可以看出，方案4的总利润不是最高的，但是737机型的利用率最高。此外，该表可以为航空公司的机队管理提供决策支持，各方案的航班机型配置表不再一一列出。

表6 机队配置方案的利润和日利用率Tab.6 Profit and daily utilization rate of fleet assignment scheme

4 结语

为了增强航空公司在市场中的竞争力，本文通过优化机型分配的方式来提高航空公司的管理水平，建立了多目标航班机型分配模型，构建了基于精英策略快速非支配排序遗传算法（NSGA-II）的多目标机型分配优化算法。通过将模型应用于国内某航空公司航线网络中，为周期为日的定期航班分配机型，对比单目标机型分配模型的机型分配方案，结果表明该算法在目标空间上分布更均匀，验证了模型的有效性。NSGA-II算法能为航班机型分配提供更多选择空间，为多目标航班机型分配的全局优化提供了一种新的思路和手段。

[1] ABARA J.Applying integer linear programming to the fleet assignment problem[J].INTERFACES,1989,19(4)：20-28.

[2] BROWN J.Airline fleet composition and deregulation[J].Review of Industrial Organization,1992,8(4)：435-449.

[3]HANE C A,BARNHART C,JOHNOSON E L,et al.The fleet assignment problem：Solving a large-scale integerprogram[J].Mathematical Programming,1995,70(2)：211-232.

[4] LISTES O,DEKKERR.A scenario aggregation-based approach for determining a robust airline fleet composition for dynamic capacityallocation[J].Transportation Science,2005,39(3)：367-382.

[5]BARNHART C,FARAHAT A,LOHATEPANONT M.Airline fleet assignment with enhanced revenue modeling[J].Operations Research,2009,57(1)：231-244.

[6] SHAO Shengzhi,HANIF D,SHERALI.A novel model and decomposition approach for the integrated airline fleet assignment，aircraft routing,and crew pairing probiem[J].Transportation Science,2015,51(1)：1-17.

[7] 徐 进.航空公司航班计划的优化方法研究[D].南京：南京航空航空大学,2007.

[8] 乐美龙,黄文秀.基于时空网络的航班机型分配问题研究[J].交通运输系统工程与信息,2014,14(1)：81-87.

[9] LIU Wanming,ZHU Xinghui,QI Yanlong.Integrated fleet assignment and aircraft routing based on delay propagation[J].Indian Academy of Sciences,2016,41(7)：713-719.

[10]朱金福.航空运输规划[M].西安：西北工业大学出版社,2008.

[11]马苏德·巴扎尔干,邵 龙.航空公司运营与规划管理[M].北京：中国民航出版社,2006.

[12]JOHN H MOTT,DANIEL HENAO,MITCHELL S HODGEN,et al.Increasing collegiate flight training fleet utilization through the use of an aircraft assignment algorithm[J].International Journal of Aviation,Aeronautics,and Aerospace,2016,3(3)：1-19.

[13]王洪涛,刘玉田.基于NSGA-II的多目标输电网架最优重构[J].电力系统自动化,2009,33(23)：14-17.

[14]JINBA T,HARADA T,SATO H,et al.Multi Objective Optimization for Route Planning and Fleet Assignment in Regular and Non-Regular Flights[C]//Proceedings of the 18th Asia Pacific Symposium on Intelligent and Evolutionary Systems,Springer International Publishing,2015：561-575.

[15]KALYANMOY DEB,AMRIT PRATAP,SAMEER AGARWAL,et al.A fast and elitist multiobjective genetic algorithm：NSGA-II[J].IEEE Transactiond on Evolutionary Computation,2002,6(2)：182-197.

（责任编辑：孟 欣）

Multi-objective for airline fleet assignment model based on NSGA-II computer engineering and applications

FAN Wei,BIE Haojie
（College of Computer Science and Technology,CAUC,Tianjin 300300,China）

Fleet assignment is one of the most important problems in airline resource optimization and management,which affects the profitability and competitiveness greatly.In order to solve the singularity of existing fleet assignment methods,a multi-objective fleet assignment model is proposed based on traditional fleet assignment models,which means that taking profit maximization and least number of aircraft as optimizational targets.However,complicated multi-objective solving model can bring bias target solving.NSGA-II algorithm is used to solve the multiobjective problem.The instance verifies the effectiveness of this method.Compared with single-objective optimization for fleet assignment model,experiment shows that the result solved by the proposed model can reach more even distribution and provide reference for decision making of airline fleet assignment.

air transportation;fleet assignment;NSGA-II algorithm;multi-objective optimization;flights

V355；TP3

A

1674－5590（2017）03－0043－06

2016-12-06；

2017-01-09 基金项目：国家自然科学基金项目（U1333109）；中央高校基本科研业务费专项（3122016B006）

樊玮（1968—），男，陕西乾县人，教授，博士，研究方向为数据挖掘、计算机软件理论与应用、智能信息处理.