一种非常用结构工业机器人D-H参数建模

吴文俊，夏 蕾，陈晓斌，方 锋，张计悦

（浙江琦星电子有限公司，浙江 台州 317600）

一种非常用结构工业机器人D-H参数建模

吴文俊，夏 蕾，陈晓斌，方 锋，张计悦

（浙江琦星电子有限公司，浙江 台州 317600）

工业机器人是现代化工业的重要组成部分。目前，大规模的工业机器人实用仿真都是以PUMA560机械结构为基础进行建模仿真研究的。在研究时，选用UR5型工业机器人，其在第4关节以后的关节相互结构关系与PUMA560的形式不同。为新型的机械机构工业机器人进行了D-H模型建模，并进行了正运动学仿真，以期为相关研究提供参考。

工业机器人；建模仿真；机械结构；D-H模型

随着全球工业现代化和智能化的发展，工业机器人在多种领域扮演着越来越重要的角色。我国工业机器人发展也随着工业4.0概念提出，并出现井喷式发展，而机器人学的研究和实际应用发展也越来越迅猛。在机器人学研究中，D-H参数建模和运动学仿真是其基础。目前，大部分工业机器人的机械结构类型类似于PUMA560型工业机器人，所有的建模和仿真大部分都是基于此机械结构类型机器人进行的研究。本文的研究对象是优傲公司的UR5型工业机器人，其在机械结构形式上与PUMA560的区别如图1所示。

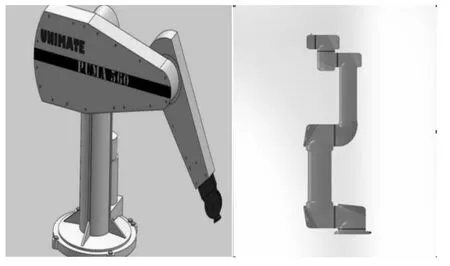
图1 PUMA560型工业机器人与UR5型工业机器人机械结构区别

从图1中可以看出，在机械结构上，对于关节1～3的相互关系，PUMA560型工业机器人与UR5型工业机器人是一致的，从第4关节开始，PUMA560的第4关节与第3关节是空间垂直关系，而UR5型工业机器人的第4关节与第3关节是平行关系，这些导致UR5型工业机器人后面第5、第6关节的空间形式都与PUMA560型工业机器人不同。在进行机器人建模与运动学仿真时，要注意以下不同之处。

1 UR5型工业机器人D-H模型建立

1.1 D-H坐标系

D-H法（四参数法）是1955年由Denavit和Hartenberg提出的一种建立相对位姿的矩阵方法。它用齐次变换描述各个连杆相对于固定参考系的空间几何关系，用一个4×4的齐次变换矩阵描述相临两连杆的空间关系，从而推导出“末端执行器坐标系”相对于“基坐标系”的等价齐次坐标变换矩阵，建立操作臂的运动方程。每个连杆由4个参数a，α，d和θ来描述，a和α描述连杆本身的特征，d和θ描述连杆之间的关系。对于转动关节，θ是关节变量，其他3个连杆参数都是固定不变的；对于移动关节，d为关键变量，其他3个连杆参数是不变的。

1.2 UR5型机器人D-H参数建立

图2 UR5型机器人坐标系建立

机械臂与关节的编号约定是：①机械臂机构中的N个运动物体从1到N编号，基座编号为0；②机械臂机构中的N个关节从1到N编号，关节i位于连杆i-1与i之间。

经过编号后，连杆坐标系约定是：①zi轴配置在关节i的轴线上；②xi-1轴位于zi-1轴和zi轴的公垂线上。

一般情况下，连杆坐标系遵循以下原则、规定：固接在连杆i-1上的坐标系{i-1}的z轴zi-1与关节轴线i-1共线，方向任意；坐标系{i-1}的x轴xi-1与连杆i-1的公垂线重合，指向从关节i-1到关节i；坐标系{i-1}的y轴yi-1按右手法则规定（食指代表x，中指代表y，大拇指代表z）。坐标系的原点取xi-1与zi-1的交点。

UR5型机器人坐标建立如图2所示。根据所设定的连杆坐标系，相应的连杆参数可以定义为：ai为从zi-1到zi沿xi测量的距离；αi为从zi-1到zi绕xi旋转的角度；di为从xi-1到xi沿zi测量的距离；θi为从xi-1到xi绕zi旋转的角度。

按照上述方法建立UR5机械臂各个连杆的坐标系，得出UR5机械臂连杆参数如表1所示。

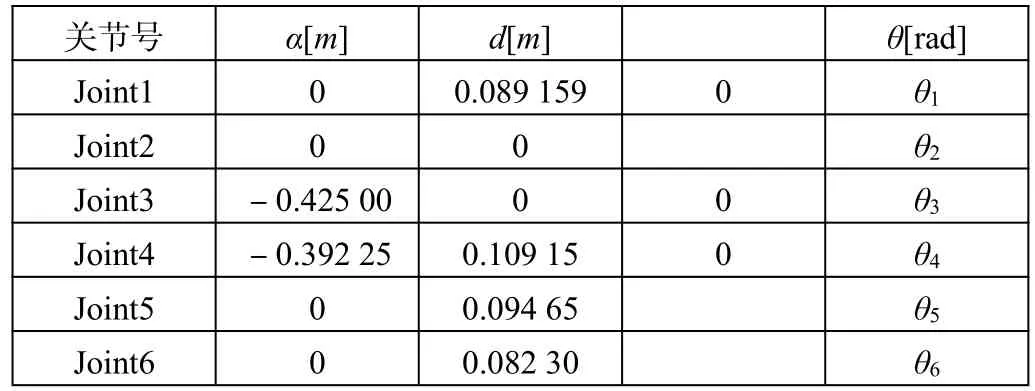
表1 UR5机械臂连杆D-H模型参数

2 UR5型工业机器人正运动学仿真

机器人正运动学的数学基础包括齐次坐标、齐次坐标变换矩阵。连杆坐标系{i}相对于连杆坐标系{i-1}的齐次变换称为连杆变换，它与这4个连杆参数有关。至此，可以把它分解为坐标系{i}的4个基本子变换问题，每个子变换只依赖于1个连杆参数，这4个子变换是：①Rot（xi-1，αi）为绕xi-1转动αi；②Trans（xi-1，ai）为沿xi-1移动ai；③Rot（zi，θi）为绕zi转动θi；④Trans（zi，di）为沿zi移动di.这是，则有：

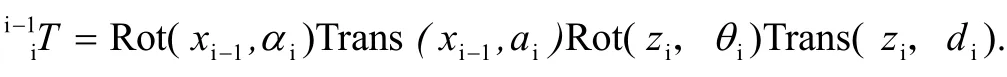
由上式右边的4个子变换得到连杆变换的通式为：

由齐次变换矩阵的乘法得：

假设每轴关节变量角度q＝[-pi/4 pi/4 pi/3 -pi/6 pi×2/3 pi/2]，根据式（1），通过6个旋转矩阵的数学相乘运算得到总变换矩阵为：

矩阵最后一列的前3个元素表示终端坐标，其坐标为[-0.137 2，0.041 0，-0.683 6]，单位M。在Matlab中的Robot Robot Toolbox工具箱中，通过RPY＝tr2rpy（t）将总变换矩阵带入，得到的3个欧拉角分别为2.356 2，-0.261 8，2.618 0.

在UR5型机器人的操作界面上，按照关节变量q输入每个关节的旋转角，运行机器人，得到的机器人位姿如图3所示。

图3 UR5型机器人实际位姿图

图3是UR5型机器人的运行数据，将其与计算数据对比，终端坐标与欧拉角的数据都吻合。本文仅列举出正运动学的一组数据，在实际工作中，需要多组数据进行验证。

3 结束语

在对非常用机械结构的工业机器人进行建模时，首先要注意其各个关节的空间特点，然后建立每个关节的坐标系，坐标系的建立是重中之重，在此基础上确定系统的D-H模型参数。建模得到的坐标系是否准确，要通过一系列运动仿真，将其与实际运行结果对比，最后确定模型建立的准确性。

［1］梁琪.全球机器人市场统计数据分析［J］.机器人技术与应用，2010（2）：26-31.

［2］王田苗，陶永.我国工业机器人技术现状与产业化发展战略［J］.机械工程学报，2014，50（9）：1-13.

［3］孙迪生，王炎.机器人控制技术［M］.北京：机械工业出版社，1998.

［4］臧庆凯，李春贵，闫向磊.基于MATLAB的PUMA560机器人运动仿真研究［J］.广西科学院学报，2010（11）：16-18.

［5］蒋刚，龚迪琛，蔡勇，等.工业机器人［M］.成都：西南交通大学出版社，2011.

［6］John J.Craig.机器人学导论［M］.原书第3版.贠超，译.北京：机械工业出版社，2006.

［7］李庆玲，刘加亮.六自由度工业机器人运动学分析及仿真［J］.机电工程技术，2008，37（11）：36-38.

［8］王智兴，樊文欣，张保成，等.基于Matlab的工业机器人运动学分析与仿真［J］.机电工程，2012，29（1）：34-37.

［9］谢斌，蔡自兴.基于Matlab Robotics Toolbox的机器人学仿真实验教学［J］.计算机教育，2010，19（10）：140-143.

〔编辑：白洁〕

TP242.2

A

10.15913/j.cnki.kjycx.2017.13.021

2095-6835（2017）13-0021-03

吴文俊（1973—），男，河南信阳人，2010年毕业于江西财经大学（硕士），国际注册能源审计师，主要从事管理与研究、电机控制与工业机器人等方面的工作。