基于多项式遍历和码字相关的Turbo码盲识别*
钟阳晶,梁茹冰
(1.广东农工商职业技术学院 计算机系,广州510507;2.华南农业大学 数学与信息学院,广州510642)
基于多项式遍历和码字相关的Turbo码盲识别*
钟阳晶**1,梁茹冰2
(1.广东农工商职业技术学院 计算机系,广州510507;2.华南农业大学 数学与信息学院,广州510642)
针对1/n码率Turbo码的盲识别问题,提出了一种基于多项式遍历和码字相关的检测识别方法。该方法首先对码字序列进行分组,利用分组验证的方法对数据中的卷积码进行快速检测,进而识别出Turbo码的码率;然后,利用欧几里得算法对Turbo码的分量编码器a的参数进行识别,进而通过对编码器b的遍历,恢复出伪随机交织序列;最后,通过与信息序列的码字相关,验证编码器b的参数是否正确,同时利用相关谱峰值所在位置识别交织器参数,实现了Turbo码的全部参数估计。仿真实验验证了该算法的有效性。对算法的误码适应能力进行的仿真分析表明,该方法能够在较高误码率条件下实现Turbo码的检测与识别。
Turbo码;盲识别;欧几里得算法;伪随机交织器
1 引 言
1993年,Berrou等提出Turbo码,通过并行编码,引入随机交织器和带有反馈的迭代译码结构,首次获得了接近Shannon理论极限的性能,成为信道编码史上的一个重大突破。Turbo码己被美国空间数据系统顾问委员会作为深空通信的标准,同时它也被确定为第三代移动通信系统的信道编码方案之一,其中具有代表性的WCDMA、CDMA2000和我国的TD-SCDMA 3个标准中的信道编码方案都使用了Turbo码,用于高速率、高质量的通信业务。国际海事卫星组织把Turbo码作为高速数据传输系统的核心技术。Turbo码已经成为下一代卫星通信系统的核心技术之一。
Turbo码由两个递归循环卷积码通过交织器以并行级联的方式结合而成,因此Turbo码的盲检测与识别可以分为卷积码的检测识别与交织器的检测识别两部分。卷积码的检测识别技术已经比较成熟[1-9]。针对交织器的检测识别,文献[10-12]分别对矩形交织器、卷积交织器和螺旋交织器等规则交织器的识别进行了研究。但Turbo码一般进行伪随机交织来获得更高的编码增益,针对伪随机交织器的识别,文献[13]给出了Turbo码的识别模型以及基本思路,但并没有对方法的容错性能进行分析。文献[14]提出了基于矩阵列向量对比的方法,使得算法具有一定的容错性能。此外,文献[15-18]还给出了基于穷举对比的方法来确定交织图案,算法需要反复进行试探、比对,计算量较大。
本文利用分量卷积码多项式阶数较低的特点,对分量卷积码生成多项式进行遍历,利用码字和遍历多项式进行信息序列还原,通过还原信息序列与真实信息序列相关谱的位置确定交织图案,实现Turbo码伪随机交织器的盲识别。
2 Turbo码编码模型
Turbo码是一种由数百码位至数千码位组成的二元分组码,图1为一个1/3码率的Turbo码编码模型,编码过程为
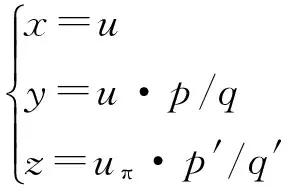
(1)
式中:u为输入信息序列,uπ为经过伪随机交织后的信息序列,x、y、z为输出编码序列,p、q、p′和q′分别为编码器a、b的生成多项式和反馈多项式。一般情况下q=q′,而p与p′则不一定相同。输出码序列为
v=x(1)y(1)z(1)x(2)y(2)z(2)…x(n)y(n)z(n)。
(2)
Turbo码的盲识别就是通过接收到的码序列v,检测是否具有Turbo编码并估计其编码多项式和交织器的交织图案。
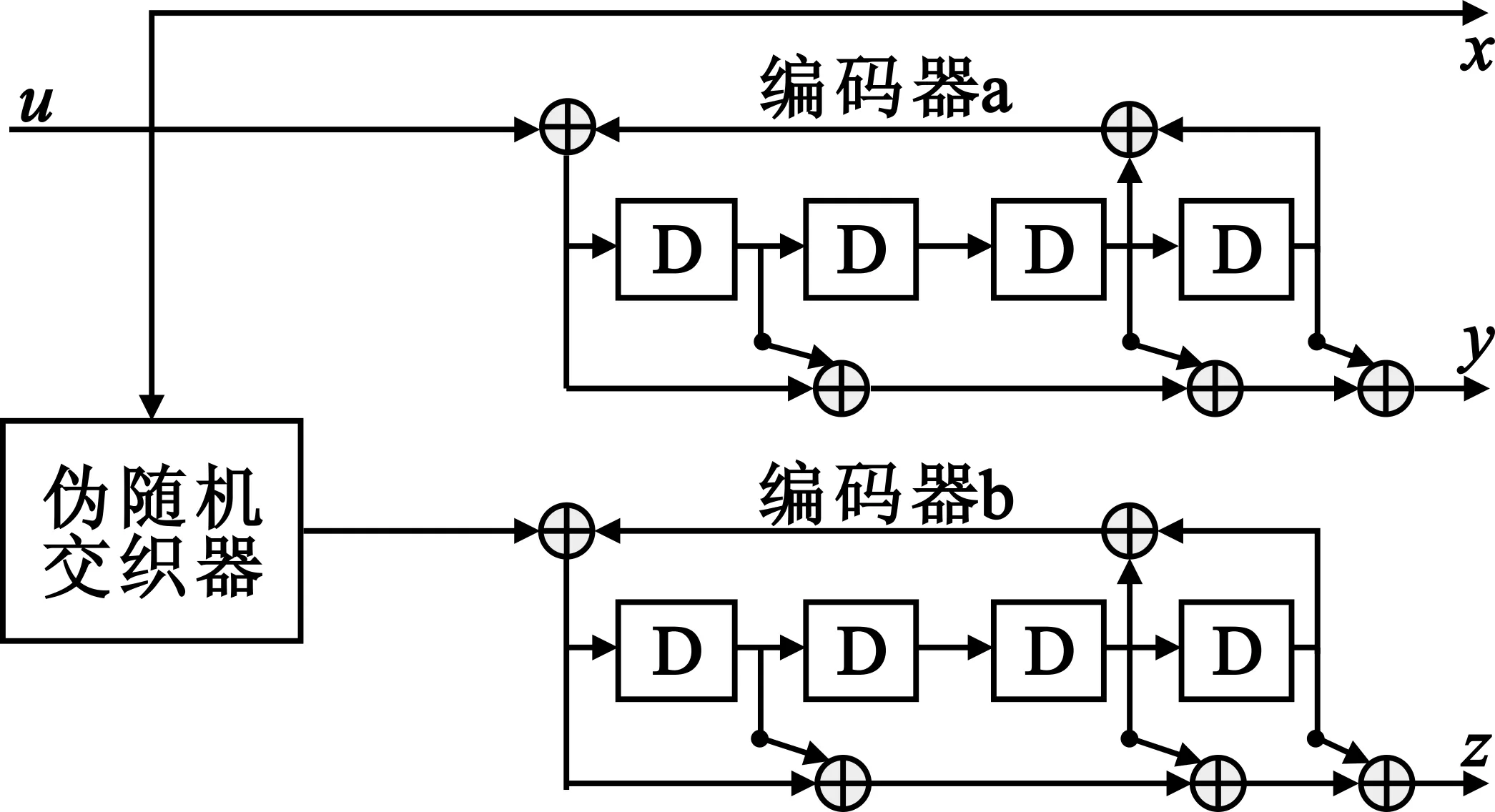
图1 1/3码率Turbo码编码器Fig.1 The encoder of 1/3 rate Turbo code
本文主要针对1/n码率的Turbo码进行识别,即信息位x保持输出不变,而通过增加编码器的数量,使得输出校验位增加,从而生成不同码率的Turbo码。根据编码器的输入端是原始信息u还是交织信息uπ可分为两大类,对于输入为u的编码器,用编码器a表示;对于输入为uπ的编码器,用编码器b表示。虽然存在多个编码器a和b,但编码器a的识别方法和编码器b的识别方法是一样的。下面分别对Turbo码的码率及编码器a和编码器b的识别方法进行论述。
3 Turbo码码率的识别
Turbo码的码率一般与第一个编码器a同时进行识别。假设Turbo码的码率为1/n,首先对接收到的码字序列分成n路序列,如果分路正确,即码率为1/n,则此时第一路数据应为原始信息序列u,第二路为第一个编码器a的输出,前两路数据构成一个1/2码率的系统反馈卷积码,可以利用欧几里得算法[1]完成卷积码的快速校验估计,具体算法详见编码器a的参数估计;如果码率不为1/n,则此时序列矩阵中的数据没有任何卷积校验关系,通过对前两路数据进行卷积码识别,不会检测出卷积码的存在。具体算法步骤如下:
输入:码字序列v。
输出:码率1/n以及分路数据。
Step 1 将码字序列按1/n(n=3)码率进行码字划分:
ci=v(i:n:end),i=1,2,…,n。
(3)
式中:(i:n:end)表示从数据第i位开始,每隔n个值截取1个值,直到数据结束。
Step 2c1表示1/n码率条件下的信息序列,将c1分别与c2进行基于欧几里得算法的卷积码快速识别。
Step 3 如果没有检测到卷积码,则n=n+1,返回Step 1;如果检测到卷积码,则表明码字分段正确,码率为1/n,同时存储ci的分路数据,i=1,2,3,…,n。当n=6时,仍没有检测到卷积码,则认为该数据中不存在1/n码率的Turbo码,此时算法退出。
4 编码器a的参数估计
编码器a的输出y与信息序列x构成了一个1/2码率的系统反馈卷积码,通过对编码器a的参数估计可以有效确定分量编码器的阶数,为编码器b的参数遍历限定一个有效范围。
由于Turbo码所使用的分量码的编码器阶数较短,一般为2~4,因此可以利用很少的码字就可以完成对其参数的有效估计,误码率对其影响较小。下面主要利用欧几里得算法[1]完成编码器a参数的快速估计。算法步骤如下:
输入:分路数据ci。
输出:编码器a的参数p、q。
Step 1 参数初始化:
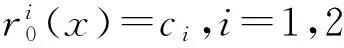
(4)
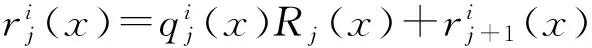
(5)
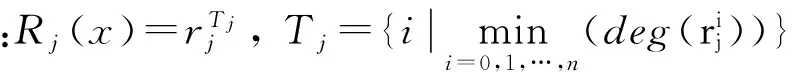
Step3 令j=j+1,重复Step2直到Tj≤L,并记录j的最大值K。
Step4 初始化hi(x):
hTK(x)=1,
(6)
hk(x)=0,k=1,2;k≠Tk。
(7)
Step 5 令j从K到1,递归计算
(8)

(9)
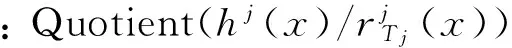
编码器阶数是未知的,因此首先假定一个大于编码器阶数的值L′。接收数据足够长的情况下L′的大小不影响计算结果,也不增加计算量。根据欧几里得算法,可得到卷积码两个生成多项式h1(x)和h2(x),将其系数转为二进制向量,即可得到编码器a的编码参数p和q。如果第i路数据与第1路数据没有检测到卷积码,则表示第i路数据的输入为交织序列uπ,则此时转入编码器b的参数估计。
5 编码器b的参数估计
对编码器a进行识别后,可以确定分量码的多项式阶数以及ci是否进行了伪随机交织。对于伪随机交织后的编码,由于uπ未知,所以难以确定p′、q′的参数。但p′、q′的阶数较低,因此可以对p′、q′进行遍历,求解相应的uπ,根据uπ与u的码字相关谱来判定p′、q′是否正确。
一般情况下,反馈多项式q=q′,因此只要对p′进行遍历即可。如图1中,多项式阶数为4,p′=x4+x3+x+1,用二进制向量表示为[11011],由于二进制向量首尾两个状态为1,因此只需对p′中间的3位进行23次状态遍历即可确定p′的状态。
令z表示加入伪随机交织后的1路编码输出,则对p′进行一次遍历后,可得到
uπ=z·q′/p′。
(10)
由于Turbo码为分组码,所以根据帧同步可以确定编码起始位置。对m组码字进行uπ的计算,得到一个m×L的码字矩阵Uπ,此时的信息序列为一个m×L的矩阵U,L编码长度,Uπ与U之间存在交织关系。假设交织器将信息序列u的第i位映射到了uπ中的第j位,则U(t,i)=Uπ(t,j),t=1,2,…,m。
由于寄存器初始状态为0,所以最前面的输出不能完全体现出寄存器的转移状态。多项式阶数为k,计算Uπ的前k+1位,如果多项式遍历正确,则Uπ的第k+1列必然对应着U中的某一列,而与其他列无关。将矩阵U化为向量模式为
U=[U(1,1)U(2,1)…U(m,1)U(1,2)U(2,2)…U(m,2)…U(L,1)…U(L,m)]。
(11)
计算Uπ的k+1列与U的相关谱
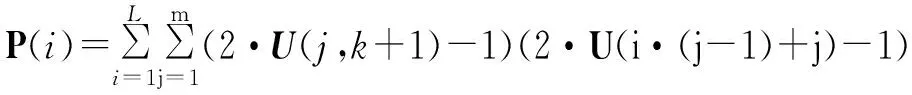
(12)
如果多项式遍历正确,则P中必然存在谱值为m的峰值分量,其峰值所在位置即为U与Uπ中第k+1列互为交织关系。
m值需要合适选择,否则m偏小可能造成相同的相关变量,交织关系出现模糊现象;m过大则增加不必要的计算量,一般选择30~50即可。编码器b参数估计的算法步骤可以概括如下:
输出:编码器b参数p′。
Step 1 根据多项式阶数k设置初始遍历多项式p′=[10…01],向量长度为k+1,对m组伪随机交织码Z分别求解相应的k+1位输入Uπ,得
Uπ(i,j)=Z(i,j)·q′/p′,i=1,2,…,m;j=1,2,…,k+1。
(13)
Step 2 计算Uπ的第k+1列与U的相关谱
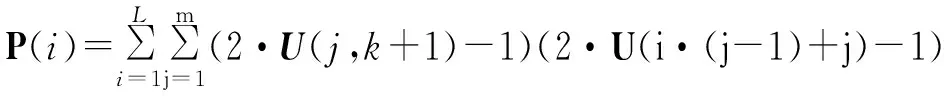
(14)
Step 3 将相关谱P与m进行比较,如果存在P(i)=m,则表明多项式遍历正确,跳出并输出结果;如果P中最大值都远小于m,则表明多项式遍历错误,则将现遍历的多项式向量中在有限域上加2,得到下一个遍历多项式,跳至Step 1,直至多项式状态遍历完毕。
6 伪随机交织器参数估计
估计出编码器b的参数后,需要对伪随机交织器的交织图案进行估计,此时根据m组码字Uπ的逐列相关检测,可以实现对全部交织图案的估计。
对m组伪随机交织码字Z按编码器b的参数进行码字还原,得到序列矩阵Uπ,对Uπ的每一列分别与向量表示的U进行相关检测,求解每次相关谱最大值的所在位置,得到长度为L的相关谱最大值所在位置向量Loc,Loc即为交织器对应的交织图案。具体步骤可以概括如下:
输入:m组码字的信息序列矩阵U和伪随机交织编码Z、编码器b参数p′。
陆九渊心学理论和社会工作增能理论两种理论,一古一今、一中一西,看似不相关,实则有着微妙的联系。通过对这两种理论进行比较,可以为西方社会工作理论的本土化和中国本土化社会工作理论的建构提供一些启示。
输出:伪随机交织器的交织图案Loc。
Step 1 根据分量码多项式p′和q′,对m组伪随机交织码Z分别求解相应输入Uπ,得
Uπ(i,j)=Z(i,j)·q′/p′,i=1,2,…,m;j=1,2,…,L。
(15)
Step 2 计算Uπ的每一列与U的相关谱
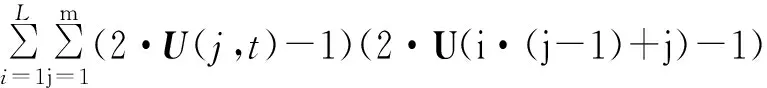
(16)
Step 3 将每一行中最大值的位置提取,得到交织对应关系
Loc(i)=max(P(i,j)),j=1,2,…,L;i=1,2,…,L。
(17)
如果Loc(1)的值为5,则表明交织器将输入u的第5位置换成了uπ中的第1位。
7 算法仿真及性能分析
仿真采用图1中的1/3码率编码器,编码长度为127,其中交织器采用伪随机交织器。当对码序列按1/3码率Turbo码截取码字时,通过欧几里得算法可以得出编码器a的多项式参数,取30组码字对编码器b的参数进行遍历,当p′=[11011]时,利用p′还原的第5列码字与信息序列的滑动相关谱如图2所示。从图中可以看出,倒数第5位的相关谱值为30,与所取码组数相同,表明p′=[11011],且交织关系为第5列与倒数第5列互换。利用该多项式参数还原全部码字,并进行码字的逐列相关便可得到交织器的全部置换关系。

图2 还原码字与信息序列的相关谱Fig.2 The correlation spectrum of recovered code and information sequence
在误码情况下,误码的存在首先会影响到分量卷积码的检测识别,由于Turbo码中分量码的多项式阶数一般小于5,误码对卷积码检测的影响较小;其次通过p′、q′对码字还原时,由于码字中存在误码,所以得到的Uπ中也存在误码,使得Uπ中列向量与U的相关谱最大值略小于m,通过增加m值和设置检测门限可以有效适应误码的存在。
分别取多项式阶数k为2~4的Turbo码,在不同误码率条件下对100组码字进行1 000次蒙特卡洛仿真,其算法的误码适应曲线如图3所示。从图中可以看出,算法可以在1%的误码条件下对Turbo码有效地进行检测和识别。
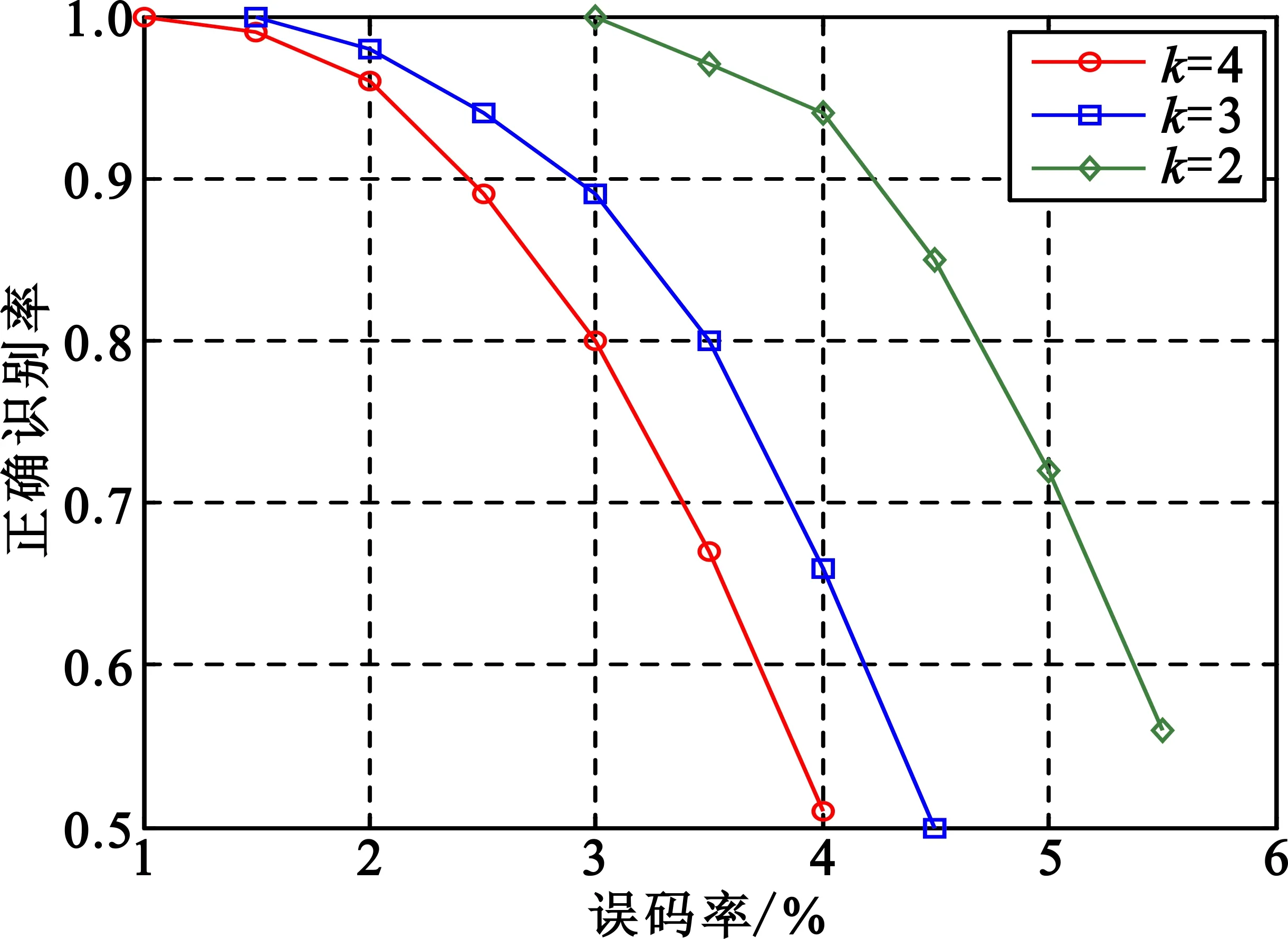
图3 Turbo码误码率与正确识别率曲线Fig.3 The curves of symbol error rate and correct recognition rate of Turbo code
算法的计算量主要体现在编码器a、b的参数估计和伪随机交织器参数估计三部分。假设多项式阶数为k,编码长度为L,并截取m组码字进行参数估计,编码器a的参数估计采用欧几里得算法,计算量为2N(2k+1),其中N为欧几里得算法所用的码字长度,在阶数小于5的1/2卷积码时,截取很短的码字长度即可,所以编码器a的参数估计所需计算量可以忽略不计。
对于编码器b的参数估计,主要为遍历不同多项式时的次数和相关谱的计算。多项式最多遍历次数为2k-1,每次遍历相关谱则需要2mL的计算量,因此编码器b的参数估计最大计算量为2kmL。而对于交织器的参数估计的计算量主要为码字还原和相关谱的计算量,码字还原需要的计算量为2(k+1)mL,而相关谱需要的计算量为2mL2,所以交织器参数估计所需计算量为2(k+1)mL+2mL2。算法总的最大计算量约为2mL2+(2(k+1)+2k)mL,在实际应用中,不会遍历全部的多项式,其计算量会有所减少。
8 结束语
本文针对1/n码率Turbo码的盲识别,提出了一种基于多项式遍历和码字相关的识别方法,仿真实验验证了算法的有效性。当码字误码率较高时,如果截获的码字数目不足,其码字相关的一阶累积量峰值不明显,会导致不能识别其中的交织关系,此时需要增加截获码字个数以适应误码率较高的情况。仿真分析表明,在截获码字个数充足(一般大于等于30)的情况下,本文算法具有较好的误码适应性能和较少的计算量。对于(n-1)/n码率的Turbo码,本文算法还不能适应,其关键在于码字分组时需要进行更多的遍历,同时对于删除图案和删除的码字部分进行补充,这将大大增加码字识别的时间和计算量。这也是下一步要重点研究的内容。
[1] LU P Z,ZOU Y. Fast computations of grobner bases and blind recognitions of convolutional codes[C]//Proceedings of the First International Workshop on Arithmetic of Finite Fields.Madrid,Spain:IEEE,2007:303-317.
[2] 刘健,王晓君,周希元. 基于Walsh-Hadamard变换的卷积码盲识别[J].电子与信息学报,2010,32(4):884-888. LIU Jian,WANG Xiaojun,ZHOU Xiyuan. Blind recognition of convolutional coding based on Walsh-Hadamard transform[J].Journal of Electronics&Information Technology,2010,32(4):884-888.(in Chinese)
[3] 柴先明,蔡凯,吕守业,等. 卷积码盲识别方法研究[J].电路与系统学报,2010,15(4):38-44. CHAI Xianming,CAI Kai,LYU Shouye,et al.Study on blind recognition of convolutional codes[J].Journal of Circuits and Systems,2010,15(4):38-44.(in Chinese)
[4] 解辉,王丰华,黄知涛. 基于最大似然检测的(n,1,m)卷积码盲识别方法[J].电子与信息学报,2013,35(7):1671-1676. XIE Hui,WANG Fenghua,HUANG Zhitao. Blind recognition of(n,1,m) convolutional code based on maximum likelihood detection[J].Journal of Electronics & Information Technology,2013,35(7):1671-1676.(in Chinese)
[5] 刘建成,杨晓静. 基于求解校验序列的(n,1,m)卷积码盲识别[J].电子与信息学报,2012,34(10):2363- 2368. LIU Jiancheng,YANG Xiaojing. Blind recognition of(n,1,m) convolutional code based on solving check-sequence[J].Journal of Electronics&Information Technology,2012,34(10):2363-2368.(in Chinese)
[6] 解辉,黄知涛,王丰华. 信道编码盲识别技术研究进展[J].电子学报,2013,41(6):1166-1176. XIE Hui,HUANG Zhitao,WANG Fenghua. Research progress of blind recognition of channel coding[J].Journal of Electronics,2013,41(6):1166-1176.(in Chinese)
[7] 杨晓静,刘建成,张玉. 基于求解校验序列的(n,k,m)卷积码盲识别[J].宇航学报,2013,34(4):568-573. YANG Xiaojing,LIU Jiancheng,ZHANG Yu. Blind recognition of(n,k,m) convolutional codes based on solving check-sequence[J].Journal of Astronautics,2013,34(4):568-573.(in Chinese)
[8] 张立民,刘杰,钟兆根.(n,1,m)递归系统卷积码的盲识别[J].电讯技术,2014,54(9):1220-1225. ZHANG Limin,LIU Jie,ZHONG Zhaogen. Blind recognition of(n,1,m) recursive system convolutional code[J].Telecommunication Engineering,2014,54(9):1220-1225.(in Chinese)
[9] 张东,陈国顺,王格芳,等. 一种新的高误码(2,1,m)卷积码盲识别方法[J].火力与指挥控制,2013,38(11):69-71. ZHANG Dong,CHEN Guoshun,WANG Gefang,et al.A new method of blind recognition to(2,1,m) convolutional code[J].Fire Control & Command Control,2013,38(11):69-71.(in Chinese)
[10] 张玉,张伟杰,杨晓静. MB-OFDM UWB系统中交织器盲识别方法[J].电路与系统学报,2012,17(1):116-119. ZHANG Yu,ZHANG Weijie,YANG Xiaojing. Blind recognition of interleaver in the MB-OFDM UWB system[J].Journal of Circuits and Systems,2012,17(1):116-119.(in Chinese)
[11] 解辉,王丰华,黄知涛. 卷积交织器盲识别方法[J].电子与信息学报,2013,35(8):1952-1957. XIE Hui,WANG Fenghua,HUANG Zhitao. A method for blind recognition of convolutional interleaver[J].Journal of Electronics&Information Technology,2013,35(8):1952-1957.(in Chinese)
[12] 廖斌,张玉,杨晓静. 螺旋形交织器交织长度盲识别[J].电子信息对抗技术,2014,29(2):14-16. LIAO Bin,ZHANG Yu,YANG Xiaojing. The blind recognition of interleaving period of helical scan interleaver[J].Electronic Warfare Technology,2014,29(2):14-16.(in Chinese)
[13] 张永光. 一种Turbo码编码参数的盲识别方法[J].西安电子科技大学学报(自然科学版),2011,38(4):167-172. ZHANG Yongguang. Blind recognition method for the Turbo coding parameter[J].Journal of Xidian University(Natural Science),2011,38(4):167-172.(in Chinese)
[14] 李啸天,张润生,李艳斌. 归零Turbo码识别算法[J].西安电子科技大学学报(自然科学版),2013,40(4):161-166. LI Xiaotian,ZHANG Runsheng,LI Yanbin. Research on the recognition algorithm of Turbo codes on trellis termination[J].Journal of Xidian University(Natural Science),2013,40(4):161-166.
[15] 武恒州,罗霄斌,刘杰. Turbo码盲识别方法研究[J].无线电工程,2015,45(5):24-27.
WU Hengzhou,LUO Xiaobin,LIU Jie. Research on blind recognition of Turbo codes[J].Radio Engineering,2015,45(5):24-27.(in Chinese)
[16] 阎剑,易正红,石荣,等. 误码条件下Turbo 码编码参数的盲识别[J].电子信息对抗技术,2014,29(3):13-16. YAN Jian,YI Zhenghong,SHI Rong,et al.Blind recognition for the Turbo coding parameter with bit errors[J].Electronic Warfare Technology,2014,29(3):13-16.(in Chinese)
[17] CLUZEAU M,FINIASZ M,TILLICH J P. Methods for the reconstruction of parallel Turbo codes[C]//Proceedings of 2010 IEEE International Symposium on Information Theory.Austin,Texas:IEEE,2010:2008-2012.
[18] CLUZEAU M,NICOLAS S. Reconstruction of a turbo-code interleaver from noisy observation[C]//Proceedings of 2010 IEEE International Symposium on Information Theory. Austin,Texas:IEEE,2010:2003-2007.
Blind Recognition of Turbo Code Based on Polynomial Traverse and Codes Correlation
ZHONG Yangjing1,LIANG Rubing2
(1. Department of Computer,Guangdong AIB Polytechnic,Guangzou 510507,China;2.Department of Mathmatics and Informatics,South China Agricultural University,Guangzhou 510642,China)
For blind recognition of 1/nrate Turbo code,an algorithm based on polynomial traverse and codes correlation is proposed. Firstly,the convolutional code is detected based on grouping check method,and the code rate of Turbo code is identified. Then the parameters of RSC(a) are estimated based on Euclidean algorithm,and the interleavered sequence is recovered by traverse of the RSC(b). The parameters of RSC(b) are validated based on the first order statistical test,and finally the parameters of interleaver are estimated by the correlation spectrum. The validity of algorithm is verified by the simulation results. Case studies are presented to illustrate that the method can recognize the Turbo code in a high noisy environment.
Turbo code;blind recognition;Euclidean algorithm;pseudo random interleaver
10.3969/j.issn.1001-893x.2017.07.015引用格式:钟阳晶,梁茹冰.基于多项式遍历和码字相关的Turbo码盲识别[J].电讯技术,2017,57(7):819-824.[ZHONG Yangjing,LIANG Rubing.Blind recognition of Turbo code based on polynomial traverse and codes correlation[J].Telecommunication Engineering,2017,57(7):819-824.]
2016-10-08;
2017-01-17 Received date:2016-10-08;Revised date:2017-01-17
广东省自然科学基金博士科研启动项目(2015A030310365)
TN911.2
A
1001-893X(2017)07-0819-06

钟阳晶(1976—),男,江西赣州人,2007年于华南师范大学获工学硕士学位,现为广东农工商职业技术学院讲师,主要研究方向为计算机软件工程和无线通信算法;
Email:zhongyangjing1976@21cn.com
梁茹冰(1980—),女,安徽合肥人,2012年于华南理工大学获工学博士学位,现为华南农业大学数学与信息学院副教授,主要从事无线通信算法、移动计算方面的研究。
**通信作者:zhongyangjing1976@21cn.com Corresponding author:zhongyangjing1976@21cn.com

