非时齐马氏过程的随机单调性
张美娟,张 铭
(1.中央财经大学统计与数学学院,北京 100081)(2.中国政法大学科学技术教学部,北京 102249)
非时齐马氏过程的随机单调性
张美娟1,张 铭2
(1.中央财经大学统计与数学学院,北京 100081)(2.中国政法大学科学技术教学部,北京 102249)
本文研究了非时齐马氏过程的随机单调性问题.利用时齐的马氏过程随机单调性的相关证明方法,加以改进,获得了非时齐马氏过程随机单调性的显式判定方法,并进一步将这一充分性条件推广为等价条件.
非时齐马氏过程;随机单调性;耦合;偏序
1 引言
耦合方法是概率论研究中使用的一个重要方法,在研究时齐的马氏过程时,曾经对耦合方法有过系统的介绍和研究(参见文献[5]第5章).关于耦合的研究及其应用,陈木法教授在这一方面有着十分重要及突出的贡献.而关于耦合方法的应用,一个重要的方面就是有关于马氏过程的随机偏序问题.
Massey[8]指出随机偏序是研究排队网络的平稳分析时很好的工具.通过随机偏序可以研究马氏过程的单调性,比较定理以及强偏序及弱偏序的问题.有关时齐的随机单调性的证明可参阅文献[5].Massey在文献[8]中给出了马氏过程随机单调性的一般性判定准则,但这一准则是从理论意义上得到的,并没有给出显式的结果.本文综合了文献[5,8]的结论及方法,给出了非时齐马氏过程单调性的显式判定方法,更方便于具体操作及应用,并将这一充分性条件的判定准则推广为等价条件.
假设状态空间()上有一个可测的偏序“”,且

定义1 如果对所有非负的单调函数f都有
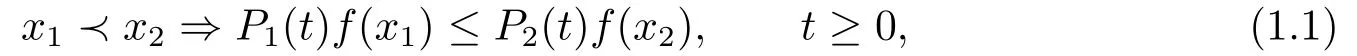
称P1(t)2(t),若P1(t)=P2(t),则称P1(t)是随机单调的.如果一个集合的示性函数是单调函数,那么这个集合称为单调集合.
对于时齐马氏过程的随机单调性,有判定方法:对于有界q对,P1(t)2(t)当且仅当其相应的q对对任意的单调集合A满足

对于非时齐的情形而言,将前面的定义推广到非时齐马氏过程中,就有
定义2 对于两个非时齐的半群Pk(s,t),k=1,2,如果对所有非负的单调函数f都有

则称P1(s,t)2(s,t).若任意的s≤t都有P1(s,t)=P2(s,t),称P1(s,t)是随机单调的.
于是参考文献[5]中的引理5.45,就得到了非时齐随机单调性的判定法则,即
定理3假设(qk(t,x),qk(t,x,dy))(k=1,2)对于t≥0是有界q对,那么P1(s,t)2(s,t)当且仅当其相应的q对对任意的单调集合A都满足
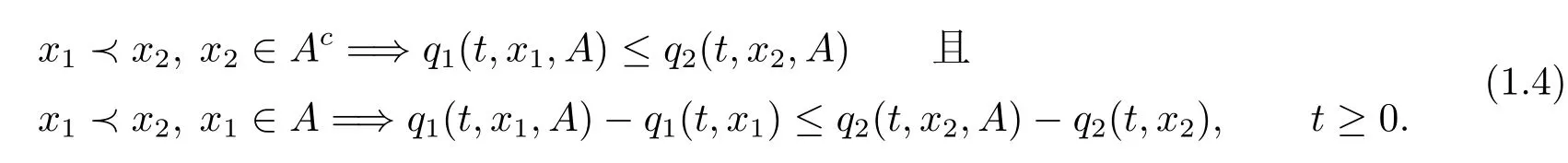
2 定理3的证明
证对于有界的q对,由文献[5]中可知存在唯一的过程P(s,t)与之对应.若有P1(s,t)≺P2(s,t),则意味着对于x1≺x2,

于是对于任意的t≥0都有

那么可以取f为示性函数IA,其中A为单调集合,于是

对于x12且x2∈Ac的情形,由于A是单调集合,所以IA(x1)≤IA(x2)=0,即x1∈Ac,于是有

那么对于x12,且x1∈A的情况,同样由于A是单调集合,所以IA(x2)≥IA(x1)=1,也就是说x2∈A.由于

于是可得

反过来,如果(1.4)式对所有的0≤s≤t都成立,那么对于任意的0≤s≤t,可以令

此时,qk(s,t)可以看做是qk(u)(u∈[s,t])的线性组合,于是对于qk(u)满足的性质(1.4)式,qk(s,t)也是同样满足的,即对于所有的单调集合A有

至此定理证明完毕.
注在这里注意到,对于保守的q对,1-P(t,t+△t;x;A)=P(t,t+△t;x;Ac),而对于x1,x2∈A,来说,类似前面的证明有

所以还可以得到对于保守的q对,(1.4)式也等价于

[1]王伟刚.一般随机环境中马氏链的强大数律[J].数学杂志,2011,31(3):481-487.
[2]Anderson W J.Continuous-time Markov chains an applications-oriented approach[M].New York:Springer,1991.
[3]Blackwell D.Finite non-homogeneous chains[J].Ann.Math.,1945,46(4):594-599.
[4]Chen M F.Eigenvalues,inequalities,and ergodic theory[M].London:Springer,2004.
[5]Chen M F.From Markov chains to non-equilibrium particle systems(2nd ed.)[M].Beijing:World Scientu fi c,2004.
[6]Chen M F,Mao Y H.Introduction to stochastic processes[M].Beijing:Higher Education Press,2007(in Chinese).
[7]Gri ff eath D.Uniform coupling of non-homogeneous Markov chains[J].J.Appl.Prob.,1975,12(4):753-762.
[8]Massey,W A.Stochastic ordering for Markov processes on partially ordered spaces with applications to queueing networks[J].Lect.Not.Mono.Ser.,Stoch.Orders Dec.Risk.,1991,19:248-260.
[9]Meyn S P,Tweedie R L.Markov chains and stochastic stability[M].London:Springer-Verlag,1996.
THE STOCHASTIC MONOTONICITY OF INHOMOGENEOUS MARKOV PROCESSES
ZHANG Mei-juan1,ZHANG Ming2
(1.School of Statistics and Mathematics,Central University of Finance and Economics,Beijing 100081,China)(2.Department of Science and Technology,China University of Political Science and Law,Beijing 102249,China)
In this paper,we study the stochastic monotonicity of inhomogeneous Markov processes. By using and improving the proof method for the stochastic monotonicity of homogeneous Markov processes,we obtain the explicit criterion for stochastic monotonicity of inhomogeneous Markov processes.Further more,this article extends this sufficient criterion to the equivalent condition.
inhomogeneous Markov processes;stochastic monotonicity;coupling;partial order
on:60J99
O211.62
A
0255-7797(2017)04-0819-04
2016-03-30接收日期:2016-04-08
中国政法大学青年教师资助计划(1000-10816108).
张美娟(1985-),女,河北石家庄,讲师,主要研究方向:随机游动,分枝过程.
张铭.
- 数学杂志的其它文章
- k-NORMAL DISTRIBUTION AND ITS APPLICATIONS
- ROSSBY WAVES WITH THE CHANGE OFβAND THE INFLUENCE OF TOPOGRAPHY IN A TWO-LAYER FLUID
- ASYMPTOTIC PROPERTIES OF A CLASS OF NONLINEAR STOCHASTIC FUNCTIONAL DIFFERENTIAL EQUATIONS WITH INFINITE DELAY
- TOTALLY UMBILICAL SUBMANIFOLD ON RIEMANNIAN MANIFOLD WITH AN ORTHOGONAL CONNECTION
- ON A SINGULAR ELLIPTIC SYSTEM INVOLVING THE CAFFARELLI-KOHN-NIRENBERG INEQUALITY
- 关于square-full数上的函数的均值估计

