A HYPERGEOMETRIC EQUATION ON THE LINE BUNDLE OVER SL(n+1,R)/S(GL(1,R)×GL(n,R))

YANG Xiang-huiHE Min-huaZHU Li

(1.School of Science,Wuhan Institute of Technology,Wuhan 430205,China)(2.School of Mathematics and Statistics,Wuhan University,Wuhan 430072,China)

A HYPERGEOMETRIC EQUATION ON THE LINE BUNDLE OVER SL(n+1,R)/S(GL(1,R)×GL(n,R))

YANG Xiang-hui1,HE Min-hua1,ZHU Li1,2

(1.School of Science,Wuhan Institute of Technology,Wuhan 430205,China)(2.School of Mathematics and Statistics,Wuhan University,Wuhan 430072,China)

In this paper,we study the di ff erential equation on the line bundle over the pseudo-Riemannian symmetric space SL(n+1,R)/S(GL(1,R)×GL(n,R)).We use Lie algebraic method,i.e.,Casimir operator to obtain the desired di ff erential operator.The di ff erential equation turns out to be a hypergeometric di ff erential equation,which generalizes the di ff erential equations in[1,3,5].

Casimir operator;pseudo-Riemannian symmetric space;line bundle;hypergeometric equation

1 Introduction

Hypergeometric functions play important roles in harmonic analysis over pseudo-Rieman nian symmetric spaces.Hyperbolic spaces are examples of pseudo-Riemannian symmetric spaces.There are a lot of work on hyperbolic spaces such as[3,4].Using a geometric method,Faraut obtained a second order di ff erential equation in the explicit case of hyperbolic spaces U(p,q;F)/U(1;F)×U(p-1,q;F)with F=R,C or H in[3].Later in an algebraic way,i.e.,through Casimir operator of sl(n+1,R),van Dijk and Kosters obtained a hypergeometric equation on the pseudo-Riemannian smmetric space SL(n+1,R)/GL(n,R)in[5].

A natural extension of[3,5]is harmonic analysis on the sections of vector bundles over pseudo-Riemannian symmetric spaces.Charchov obtained a hypergeometric equation on the sections of line bundles over complex hyperbolic spaces U(p,q;C)/U(1;C)×U(p-1,q;C)in his doctor thesis[1].The di ff erential equation in[1]is the same as the one in[3].In this paper we will follow the method in[6]to obtain the hypergeometric equation on the sections of line bundles over SL(n+1,R)/GL(n,R).When the parameterλis zero,our result degenerates to the di ff erential equation in[5].Our hypergeometric equation will be used to obtaining the Plancherel formula on the sections of the line bundle over SL(n+1,R)/S(GL(1,R)×GL(n,R))in a future paper.

2 Preliminaries and Main Result

LetG=SL(n+1,R)andH1=SL(n,R).We imbedH1inGas usual,i.e.,for anyLetHbe the subgroup ofG：

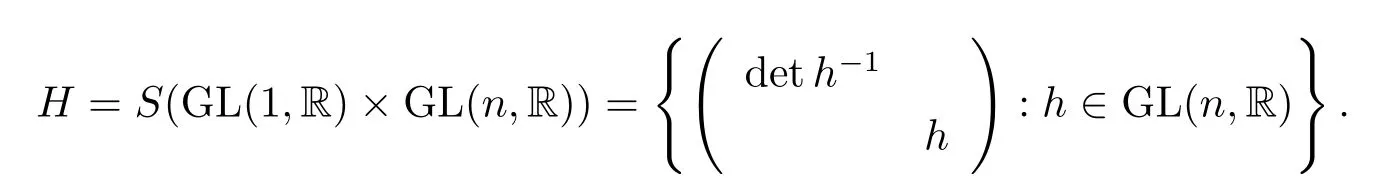
In what followstAdenotes the transpose of a matrixA.LetX1be the algebraic manifold of

defined by

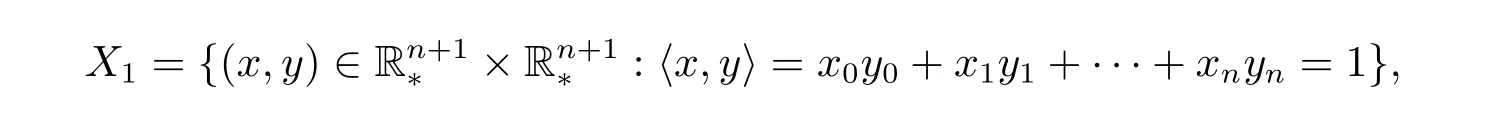
for anyg∈Gand any(x,y).With this action,X1is transitive underG.Letx0=(e0,e0)∈X1wheree0is the fi rst standard unit vector in Rn+1,i.e.,e0=t(1,0,···,0).Then the stabilizer ofx0inGisH1.An elementary proof shows thatX1≃G/H1.We also haveX≃G/HwhereX={x∈Mn+1(R)：rankx=trx=1},here Mn+1(R)is the space of all real(n+1)×(n+1)matrices.Gacts on Mn+1(R)by conjugation(see[5])

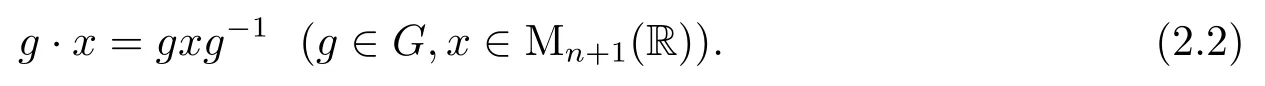
Let g=sl(n+1,R)be the Lie algebra ofG.The Killing form of g isB(X,Y)=2(n+1)trXYforX,Y∈g.The Killing form induces a measure onX1.With this measure,the Casimir operator Ω of g induces a second order di ff erential operator onX1.We call it the Laplace operator and den√ote it as□1.

Forλ∈R,set√be a continuous unitary character of R∗.De fi ne a

characterχλofHasfor

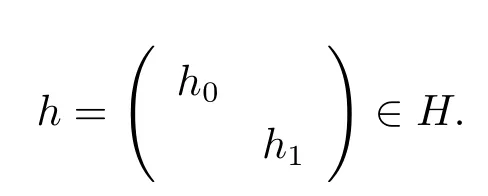
LetD(X1)be the space of complex-valuedC∞-functions onX1with compact support.The action ofGonX1induces a representationUofGinD(X1)：

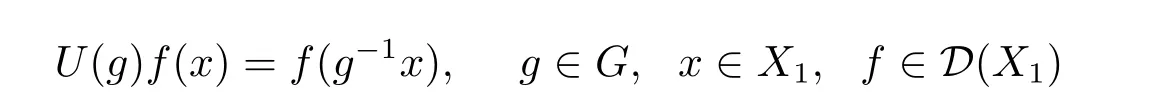
and by inverse transposition a representationUofGinD′(X1).

We define

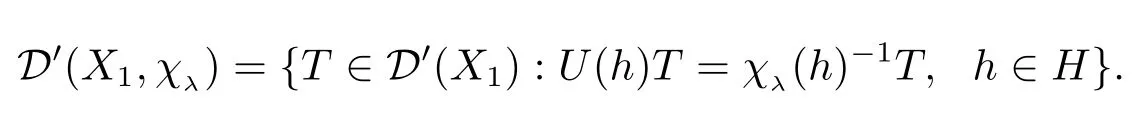
Becauseχλ=1 onH1,the above distributionsTcan be viewed as the bi-H1-invariant distributions onGsatisfyingU(h)T=χλ(h)-1T,h∈H.

Ifµ∈C,define

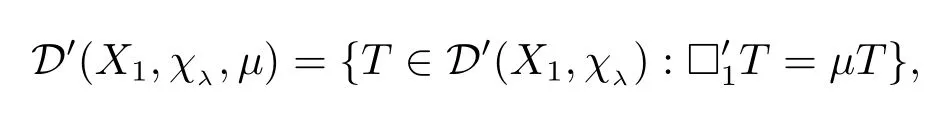
De fi nition 2.1Theχλ-spherical distributionsTonX1are the distributions onGsatisfying the following properties

•TisH1-invariant,

•T(hx)=χλ(h)T(x),h∈H,x∈X1,

•□′1T=µTfor someµ∈C.

As in[2],we define a mappingQ1：X1→R byQ1(x,y)=x0y0.We take the open subsetsX01={ (x,y)∈X1：Q1(x,y)＜1}andX11={ (x,y)∈X1：Q1(x,y)＞0}ofX1.

There is an averaging mappingdefined by

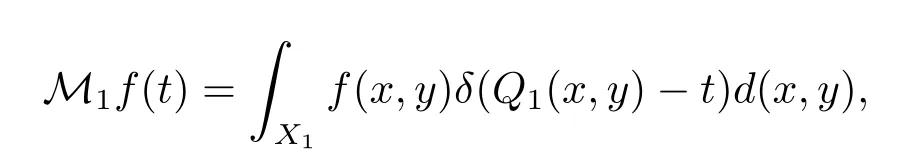
whereδis the Dirac measure andd(x,y)is aG-invariant measure onX1.De fi neξ：X1→R2

byξ(x,y)=(ξ1(x,y),ξ2(x,y))=(x0,y0).Thenwhereis the adjoint ofM1.Then we have the main theorem of this paper.

Theorem 2.1There is a second order di ff erential operatorLλon R such that the following formula holds

where

3 Proof of Main Result

We take a basis of g=sl(n+1,R)as

whereEαβ=(δαµδβν)µνis as usual.

OnX1we take the coordinates{x0,y0,x1,y1,···,xn-1,yn-1,xn}.Using(2.1),we followthe way in[6]to expressEαβas di ff erential operators onX1in terms of the coordinates{x0,y0,x1,y1,···,xn-1,yn-1,xn}.The results are

Following[1],let the functionFonX1be the formF(x,y)=F(x0,y0).We calculate the action of the Laplace operator □1or the Casimir operator Ω on such functions.BecauseFdepends onx0,y0only,we take Ω as

where the ‘other terms’are the combinations ofEkl(2≤kl≤n+1).With the coordinates{x0,y0,x1,y1,···,xn-1,yn-1,xn},using(3.1)-(3.5),we have

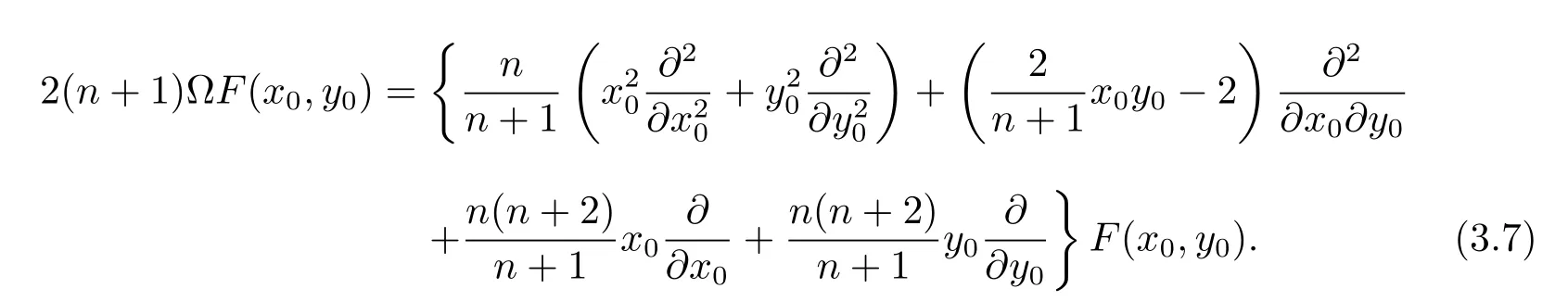
Now taking functionF(x0,y0)with the formwe obtain

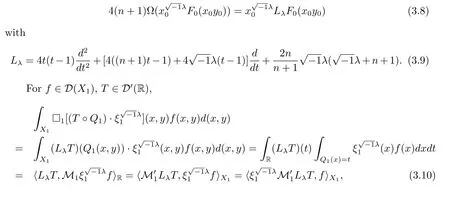
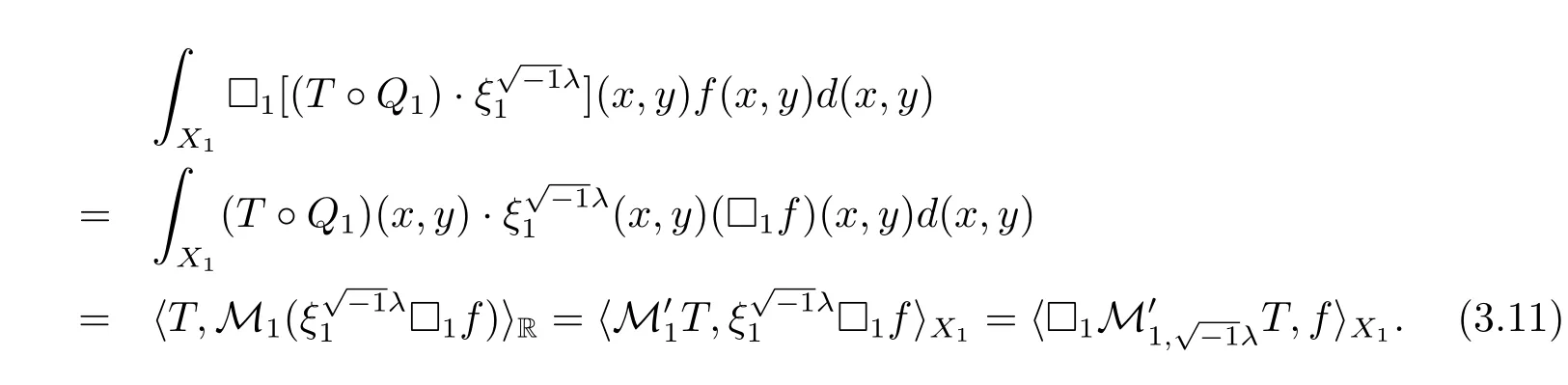
Comparing(3.10)and(3.11),we haveThis completes the proof of Theorem 2.1.

[1]Charchov I.Harmonic analysis on line bundles over complex hyperbolic spaces[D].Leiden：Univ.Leiden,1999.

[2]van Dijk G.(GL(n+1,R),GL(n,R))is a generalized gelfand pair[J].Russian J.Math.Phys.,2008,15(4)：548-551.

[3]Faraut J.Distributions sphriques sur les espaces hyperboliques[J].J.Math.Pures Appl.,1979,58：369-444.

[4]Han Yingbo,Feng Shuxiang.On complete hypersurfaces in hyperbolic space formHn+1(-1)[J].J.Math.,2013,33(5)：767-772.

[5]Kosters M T,van Dijk G.Spherical distributions on the Pseudo-Riemannian space SL(n,R)/GL(n-1,R)[J].J.Funct.Anal.,1986,68：168-213.

[6]Lang S.SL2(R)[A].Volume 105 of Graduate Texts in Mathematics[C].Reprint of 1975 ed.,New York：Springer-Verlag,1985.

SL(n+1,R)/S(GL(1,R)×GL(n,R))上线丛的一个超几何方程

杨向辉1,何敏华1,朱 理1,2

(1.武汉工程大学理学院,湖北武汉 430205)(2.武汉大学数学与统计学院,湖北武汉 430072)

本文研究了伪黎曼对称空间SL(n+1,R)/S(GL(1,R)×GL(n,R))线丛上的微分方程.利用李代数方法,即Casimir算子得到这个微分算子.这个微分算子是一个超几何方程,这个结论推广了文献[1,3,5]中的微分方程.

Casimir算子;伪黎曼对称空间;线丛;超几何方程

O152.5

on：22E46;33C05

A Article ID： 0255-7797(2017)04-0667-05

date：2016-05-27Accepted date：2016-07-11

Supported by the Research Foundation of Education Department of Hubei Province(Q20121512).

Biography：Yang Xianghui(1980-),female,born at Xiantao,Hubei,lecturer,major in functional di ff erential equations.