基于Mixture两相流模型和准静态方法的积雪分布数值模拟

薛铭乾 黄慧萱

(西南交通大学土木工程学院，四川 成都 610031)



基于Mixture两相流模型和准静态方法的积雪分布数值模拟

薛铭乾 黄慧萱

(西南交通大学土木工程学院，四川 成都 610031)

在风致雪运动的研究中，采用基于Fluent提供的Mixture两相流模型，并结合准静态方法，对二维防雪栏开展数值仿真，分析了防雪栏离地面的高度对地面积雪分布的影响，验证了该方法的可行性与准确性。

风致雪漂移，数值模拟，两相流，准静态方法

0 引言

风致雪运动的数值模拟开始于20世纪90年代。2002年Alhajraf[2]使用Flow-3D软件对复杂建筑的周边积雪进行了数值模拟，并使用了FAVOR技术对积雪边界进行调整；2009年Thiis[3]使用了两相流的方法进行了三维大跨曲面屋盖的积雪模拟，在模拟中采用了瞬态计算方法；2011年莫华美[4]采用两相流理论对一些典型屋面进行了二维的数值模拟，在模拟中使用Fluent中的Mixture模型，并使用了Fluent的动网格技术；2016年周晅毅[5]提出了采用准静态方法来模拟。

本文采用Euler-Euler两相流模型，使用Fluent中的Mixture模型完成数值模拟。由于瞬态计算十分耗时，尤其是三维模型的模拟，因此本文采用准稳态方法模拟，并考虑了积雪休止角的影响[6]。

1 风致雪漂移数值模拟方法

在风致雪运动的研究中，通常采用Euler-Euler两相流理论，本文采用Fluent两相流模型中的Mixture模型，并配合雪边界调整。

1.1 Mixture模型

在Fluent中，Mixture模型是一种简化的多相流模型，是通过求解混合相的连续方程、动量方程和能量方程，次相的体积分数运输方程和各相之间的相对速度来模拟多相流的运动。

体积分数方程：

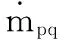
1.2 湍流模型

在现阶段的研究里，湍流的模拟上没有定论，然而湍流模型事关风场模拟的精度与准确度，因此湍流模型的选择十分关键，也依然是现在的研究热点。由于k-ε模型具有较好的普适性，因此往往是工程计算的普遍选择，因此本文采用Realizablek-ε湍流模型。

1.3 雪的沉积与积雪的侵蚀

雪的沉积与侵蚀和积雪边界上的剪切风速u*与剪切风速阈值u*t有关，同时也和流场内雪相浓度相关，并忽略温度、压强等次要因素。当地的剪切风速由流场特性确定，剪切风速阈值的相关因素就相对复杂，自然条件下雪的剪切风速阈值大致在0.15～0.40之间。当剪切风速u*大于剪切风速阈值u*t时，表现为积雪的侵蚀，反之则为雪的沉积，积雪侵蚀通量qero和雪的沉积通量qdep分别为：

因此积雪边界上的通量改变值qs=qero+qdep，从而可以得到积雪边界高度改变量Δh：

其中，Δt为时间步长；γ为积雪中雪相的最大体积分数，一般取值为0.62。

2 算例分析

防雪栏可以改变局部空气流动规律，可以改变积雪在防雪栏附近的堆积形态，常用于铁路和公路的风雪防护中。由于防雪栏在长度方向远大于宽度、高度，因此可以被视为二维问题。

2.1 几何建模及计算参数

该算例来自于Uematsu(1991)的数值模拟，其中的实测数据来自于Takeuchi(1989)。如图1所示，其计算流域大小为40m×140m，其中防雪栏上游长度为40m，下游长度为100m，防雪栏的尺寸为高3.41m、宽0.1m。设置两组模型，控制防雪栏到地面的高度，分别为0.1m和0.4m，其他参数一致。

雪的密度ρs=150kg/m3，雪颗粒的下降速度wf=0.20m/s，雪粒子直径取为0.15mm，剪切速度阈值u*t=0.20m/s。

由于该模型模拟的是在防雪栏作用下的地面积雪，因此在建模及计算中没有考虑休止角，不预铺雪，主要考虑雪的沉积效应。

2.2 边界条件

1)入流边界。

使用速度入口边界，大气边界层的水平风速呈对数分布，v=w=0：

其中，κ为冯卡门常数；z0为气动粗糙长度。

雪相体积分数的入口条件中，需要区分跃移运动和悬移运动，跃移层的高度为：

入口处跃移层和悬移层的雪相体积分数分别为：

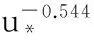
2)出流边界。

采用完全发展的出流边界。

3)计算流域的顶面与侧面。

设置对称边界条件。

4)地面及防雪栏表面。

采用无滑移边界。

2.3 计算方法及流程

在自然条件下，风吹雪现象会持续几个小时到数天不等，若使用常规手段进行非定常计算，计算量极大且非常耗时。因此考虑到计算的精度及效率，而采用准静态方法。该方法的计算流程如下：

1)根据计算模型参数及其他信息确定数值模拟时间T，并分成n个时间段，第i个时间长度表示为Δti。

2)通过Fluent多相流模型中的Mixture模型计算风场及其雪相浓度分布，从而得到积雪表面的剪切风速u*和雪相体积分数f。

3)由步骤2)计算得到的结果，并根据公式确定雪相通量的改变值qs，并计算积雪边界的高度改变量Δhi。

4)将步骤3)计算所得的高度改变量Δhi更新到计算网格中，其中包括调整边界及边界附近网格，形成下一个时间段的计算网格。

5)重复步骤2)～3)，完成整个数值模拟。

在这个方法中，采用有限个定常计算来取代非定常计算，在计算效率上来说是可取的。风吹雪现象持续的时间很长，边界上的改变量是一个有限的量，当边界高度改变量较小时，边界改变引起的流场变化可以忽略，因此将整个模拟分成n个阶段，在计算精度上是可以接受的。

准静态方法里的核心问题在于阶段数目和每个阶段持续时间的确定。阶段数目取决于模拟的总时长以及流场的稳定程度。由于在每个阶段内被当成定常问题来处理，因此倘若流场对边界变动较为敏感时，单阶段的模拟时长不宜过长。

3 计算分析

考虑防雪栏距离地面高度对积雪形态的影响，其中离地高度h分别为0.1m和0.4m，其中第二个模型为验证算例。

图2a)为防雪栏距离地面h0=0.4m情况下初始阶段的水平风速分布，防雪栏后部存在一个较大的回流旋涡，在防雪栏后部较远(x>15)的地面上存在更大的回流旋涡。由于防雪栏距离底部还有0.4m，有大量气流通过，风速较大。图2b)则为防雪栏距离地面 0.1m的水平风速分布，两者风速分布规律相似，但存在少量差异：防雪栏后部的旋涡比前者小一些；地面上的回流旋涡位置向前挪动了(大概位置在x>10)；由于防雪栏距离地面的高度变小，底部通过的气流变少，底部风速比前者低。

将整个数值仿真过程分成三个阶段，分别做两次网格调整。

图3为验证算例的数值仿真结果，取防雪栏高度H=3.41m为特征高度，对坐标X和积雪高度S做归一化(同下)。从三个阶段的仿真结果来看，对比分析三个阶段中积雪堆积位置以及积雪增量，认为流场中的风场对积雪边界的变化不敏感。

对比数值仿真和实测结果可以发现，防雪栏上游，数值仿真的积雪堆积与实测结果吻合的较好，而防雪栏后部则吻合的较差。防雪栏上游的空气流动没有受到扰动，流场的仿真结果与实际相差不大，但下游则受到防雪栏的扰动，空气流动变得复杂，脉动特征增强，湍流模型难以捕捉流场特征，因此流场的模拟效果相对较差；同时由于Takeuchi等人所使用的防雪栏是存在14%的孔隙率，然而在数值仿真中并未考虑，因此下游区域的流场仿真与实际有较大出入。在模拟中，防雪栏下游区存在积雪堆积，大致位于2.8≤x/H≤4.5，其规律与实测相似。总体上而言，数值仿真结果可以接受，因此认为本文提出的数值仿真方法可行。

图4为防雪栏距离地面0.1 m的三阶段数值仿真结果，其中反映出来的规律与验证模型一致，存在少许差异(见图5)：防雪栏上游，两者差距不大，但是靠近防雪栏位置的积雪坡度随高度h0的减小而增大；防雪栏下游的积雪堆积位置要比验证模型靠前，大致位置在1.3≤x/H≤3.0。

4 结语

本文提出了一种基于Fluent的Mixture两相流模型和准静态方法的数值模拟方法，能够提高风致雪漂移数值模拟的计算效率。通过对二维防雪栏地面积雪分布的数值仿真，验证这种数值模拟方法的可行性，并分析防雪栏距离地面高度不同所带来的差异。本文得出如下几个结论：

1)将二维防雪栏的数值仿真结果与文献实测数据进行对比，验证了这种数值模拟方法的可行性。

2)随着防雪栏距离地面的高度的减小，上游的积雪堆积变陡，下游的积雪堆积向前移动。

[1] Sato T,Uematsu T,Nakata T,et al.Three dimensional numerical simulation of snowdrift[J].Journal of Wind Engineering and Industrial Aerodynamics,1993(46):741-746.

[2] Alhajraf S.Numerical simulation of sand and snow drift at porous fences[A].Proceedings of the Fifth International Conference on Aeolian Research and the Global Change and Terrestrial Ecosystem-Soil Erosion Network[C].2002:208-213.

[3] Thiis T K,Potac J,Ramberg J F.3D numerical simulations and full scale measurements of snow depositions on a curved roof[A].5th European & African Conference on Wind Engineering,Florence,Italy[C].2009.

[4] 莫华美.典型屋面积雪分布的数值模拟与实测研究[D].哈尔滨：哈尔滨工业大学,2011.

[5] Zhou X,Kang L,Gu M,et al.Numerical simulation and wind tunnel test for redistribution of snow on a flat roof[J].Journal of Wind Engineering and Industrial Aerodynamics,2016(153):92-105.

[6] 康路阳,周晅毅,顾 明.考虑积雪休止角的屋面积雪漂移数值模拟方法[J].同济大学学报(自然科学版),2016(1):11-15.

Numerical simulation of snow distribution based on Mixture two-phase flow model and quasi-static method

Xue Mingqian Huang Huixuan

(School of Civil Engineering, Southwest Jiaotong University， Chengdu 610031， China)

In the research of wind-induced snow movement, a numerical simulation method based on Mixture two-phase flow model from Fluent combined with quasi-static method is adopted. Through the numerical simulation of two-dimensional snow-proof bars, this method is tested and the influence of the height of the snow protection bar on the ground snow distribution is analyzed.

snowdrift, numerical simulation, two-phase flow, quasi-static method

1009-6825(2017)16-0041-03

2017-03-22

薛铭乾(1991- )，男，在读硕士； 黄慧萱(1962- )，男，副教授

TP319

A