基于需求更新的班轮舱位预订决策与协调策略
孔凡强, 曲林迟, 徐 朗
(上海海事大学 经济管理学院,上海 201306)
基于需求更新的班轮舱位预订决策与协调策略
孔凡强, 曲林迟, 徐 朗
(上海海事大学 经济管理学院,上海 201306)
鉴于即期货主需求较难准确预测,使得班轮舱位订货存在很大不确定性的情况,班轮公司为保证自身利润,往往要求船代公司采取批量订舱的策略.基于市场需求信息更新的情况,建立了两阶段班轮企业和船代企业的利润模型,比较了集中决策和分散决策下两种策略的优劣和获得利润的大小,并通过设计有效的班轮舱位回购契约对供应链进行有效的协调,以实现班轮公司和船代公司各自的供舱量和订舱量决策达到集中决策时的最优水平,从而使得供应链成员实现共赢.最后,通过算例分析对模型进行验证和说明.
班轮运输; 舱位预订; 两阶段决策; 回购契约
班轮舱位作为具有显著易逝品特征的商品,往往会随着时间的变化而导致其使用价值不断下降[1-3].航运市场的周期波动性和货主订舱信息的不可预知性,增加了舱位控制的难度.而不景气的世界经济使航运相关企业的竞争日益加剧,如何利用供应链管理的思想整合航运业的资源显得尤为重要.而航运相关企业是否加入供应链参与合作,取决于加入供应链所能获得的利润是否多于所作的投资以及单独营运时的利润[4-5].所以,如何正确地得到市场信息、科学地确定船代公司订舱量和班轮公司供舱量、有效地对供应链进行合理的协调,对于降低企业运营成本,提高企业效益有着现实意义.
1 研究现状
在船代公司运营过程中,订舱量是最为关键的决策要素之一,合理的订舱量既可以减少社会资源的浪费,同时也能减少班轮舱位随时间推移而贬值的危险.李冰州等[6]在对舱位进行配置时考虑了空箱调运及路径选择的情况,但需求采用确定型数据,没有充分考虑需求的随机性及其分布特征.王琳等[7]在产能固定的情况下,构建了基于货主选择行为的易逝品订货决策模型,并发现不同货主单位订货价格对最优订舱量的影响是有差异的.Lu等[8]立足于为班轮公司能够提供满足周期性需求的班轮服务,着重研究相关价格因素对舱位配置结果造成的影响.倪冠群等[9]针对乘客未来订票信息不可预知的价格和舱位控制问题,从在线策略和竞争分析角度,设计了最优的价格和座位在线联合控制策略.徐贤浩等[10]考虑产品易逝性的特点,构建了完全理性、允许缺货以及价格折扣3种状态下的库存模型,并针对变质率对需求率的影响进行了探讨.王圣东等[11]考虑订货具有固定费用以及未满足需求延期供给等现实因素,建立了动态环境下的销售商两阶段订货决策模型,提出了寻求订货策略的简单方法,探讨了订货决策与需求波动以及延期供给率的关系.上述文献所建立的模型虽然是对实际问题的提炼和概括,但都忽略了订货决策的多周期性和相互关联性.同时上述文献仅探讨了船代公司的订货决策问题,未将模型推广到由班轮公司和船代公司所组成的两级供应链的生产和订货决策中.
目前,国内外学者在不确定市场上产品需求预测的研究已取得不少成果.尚文芳等[12]引入期权契约讨论易逝品供给与需求的关系,并对供应链进行了帕累托改进,通过仿真计算发现供应链新增利润的分配与期权购买价格是相互关联的.陈旭[13]对开始时刻和顾客需求信息更新后的船代公司利润进行比较和分析,得到了在两次订货条件下船代公司应该采取的优化订货与调整策略.Kurawarwala等[14]在贝叶斯模型的基础上进行了相应的改进,对具有易逝性产品的需求进行了参数估计和预测,对企业控制库存具有理论价值和现实意义.宋华明等[15]假设需求预测误差和赶工成本分别与提前期成对数和分段线性关系,研究了需求预测更新的易逝品供应链合作策略问题.Choi等[16]研究了两种不同的信息更新QR模型,指出有效的QR策略需要准确的需求信息更新,而且需要对销售季节前的产品通过观测从而进行合理选择.Ouyang等[17]把提前期看作可控的决策变量,研究了提前期缩短带来的收益与增加的赶工成本之间的权衡问题.陈金亮等[18]利用船代公司第一次订货后观测到的市场需求信息来修正前期预测,对船代公司第二次订货修正,从而降低一次订货的非准确性造成的损失.然而,上述文献无论是从企业角度,还是从多周期信息更新角度,均假设周期间的需求信息是相互独立的非随机过程.
本文以不确定环境下的易逝品作为研究对象,在需求信息更新的条件下,建立了以两阶段报童模型作为基础的易逝品两级供应链决策模型,通过求解得到了供应链系统的班轮公司生产决策和船代公司订货最优决策.比较了集中决策和分散决策下供应链成员和整体的利润,并利用回购契约对供应链进行了协调,对班轮公司和船代公司运营管理具有重要的理论价值和较强的现实意义.
2 模型描述与基本假设
单个班轮公司和单个船代公司组成两级供应链系统,由该系统提供并销售班轮舱位.班轮公司给予船代公司两次订货机会,在此期间船代公司不断收集更新市场需求信息,从而提供更准确的需求预测,但同时必须将更新的需求预测告知班轮公司.而班轮公司根据船代公司的舱位订单,分别进行两次船舶调度,然后将班轮舱位一次性交付给船代公司进行销售,如图1所示.
2.1 符号说明
为了便于理解,将模型中的符号在表1中列出.

图1 信息更新下的两阶段供舱与订舱Fig.1 Two-stage allocating and booking slots under the information updating表1 模型符号说明Tab.1 Description of symbols in the model

符号说明x市场需求,其概率分布函数为F(x),概率密度函数为f(x),E(x)=μ,D(x)=σ2xe信息更新后市场需求,其概率分布函数为F(x|xe),概率密度函数为f(x|xe)s缺货时船代公司承担的产品缺货成本v销售结束后,单位产品的残值r单位产品的零售价格ci第i阶段的班轮公司单位舱位成本qi第i阶段班轮公司舱位供给量,q1+q2=Qdi第i阶段船代公司订舱量,d1+d2=Dwi第i阶段的班轮公司批发价格b班轮公司对未销售产品的回购契约价格F-1(di|xe)在xe条件下,第i阶段的船代公司订舱量,且xe(di)≡argmaxF(di|xe)F-1(qi|xe)在xe条件下,第i阶段的班轮公司供舱量,且xe(qi)≡argmaxF(qi|xe)D(xe,q1,q2)在xe条件下,船代公司第二阶段订货决策Q(xe,q1,q2)在xe条件下,班轮公司第二阶段生产决策
2.2 模型假设
为了便于建立具体的决策模型,首先给出如下假设:
a.市场需求信息是完全的,即班轮公司和船代公司对双方的成本结构和市场需求分布是已知的;
b.班轮舱位的市场价格在一定时期内保持不变,市场需求是非负的随机变量,其概率分布函数和概率密度函数均为连续可微函数;
c.为便于计算,班轮公司的成本主要包括班轮调运成本,由于第一次班轮调运距离订舱截点时间较远,班轮公司有较为充足的调船时间,所以班轮公司两阶段单位舱位成本满足c1 d.班轮公司和船代公司均为风险中性,以自身利润最大化为前提进行决策; e.参考王琳等[7]的研究成果,班轮公司和船代公司组成两级供应链,其决策构成Stackelberg博弈,班轮公司是领导者,船代公司是跟从者. 3.1 集中决策模型 在集中式供应链系统中,班轮公司和船代公司作为同一决策者,以供应链整体利润最大化为目标,分别确定两阶段的最优供舱量(q1,q2),从而使供应链系统获得最大的期望利润. 式中,上标C代表集中决策. 其中, 引理1 当供应链进行集中决策时,利润函数πsc是关于两阶段供舱量q1,q2的严格凹函数,且两阶段最优供舱量有如下关系: 引理2 当供应链进行集中决策时,供应链第一阶段供舱量满足第一阶段订舱量时,为获得最大利润,其第一阶段最优供舱量为 其中, 可以发现,集中决策情况下供应链的订货策略和生产策略与市场需求可知程度xe和两阶段生产成本差值c2-c1有关. 3.2 分散决策模型 在分散式供应链系统中,班轮公司与船代公司之间采取斯坦博格博弈.运用逆序求解法可求得供应链成员最优决策.首先,船代公司根据班轮公司提供的两阶段不同的批发价格确定其两次的订舱量.接着,班轮公司依据船代公司的订单确定每阶段的供舱量.根据契约约定,班轮公司的总供舱量必须满足船代公司的总订舱量.所以,班轮公司和船代公司的利润函数分别为 式中,上标D代表分散决策. 其中, 引理3 当供应链进行分散决策时,船代公司的利润函数πr是关于两阶段订舱量d1,d2的严格凹函数,且两阶段最优订舱量有如下关系: 引理4 当供应链进行分散决策时,班轮公司第一阶段供舱量满足第一阶段订舱量时,为获得最大利润,其第一阶段最优供舱量为 由引理4可以发现,在分散式决策情况下,由于供应链成员均从自身的角度考虑供舱量与订舱量,从而导致了“双重加价”[19]现象的出现,两者的供舱量和订舱量都小于集中决策下的最优决策.因此,两者的期望利润也都小于集中决策情况下的期望利润. 3.3 基于舱位回购的供应链协调策略 针对信息更新和时效性,采用舱位回购策略对班轮公司和船代公司构成的两级供应链进行协调,实现供应链成员整体效益达到集中决策的水平.也就是说,通过契约b激励班轮公司的供舱量和船代公司的订舱量与集中式系统的最优决策相一致[20].所以,回购条件下的班轮公司和船代公司利润函数分别为 式中,上标R代表协调策略. 其中, 其中, 引理6 当进行回购契约时,满足如下条件时供应链即可实现完美协调. 为达到供应链协调,班轮公司应对船代公司提出回购,处理剩余舱位并对船代公司进行一定的补偿.如果缺货时班轮公司承担缺货损失,则应提高第一阶段供舱批发价和回购价格,才能使得船代公司的订舱量达到集中决策的最优解. 为了验证模型的准确性和有效性,下面通过数值仿真进一步分析各个决策变量、供应链各成员及整体利润与参数之间的关系.根据文献[21],假设市场需求x=xe+ε,ε为独立误差且服从正态分布,E(ε)=0,D(ε)=σ2.更新后的市场需求xe服从均匀分布,E(ε)=μ,D(ε)=σ2+δ2/3,δ为误差偏离程度.模型的基本参数如表2所示 表2 参数设置Tab.2 Setting of parameters 3种不同供应链系统模型的各成员利润和整体利润,以及船代公司订舱量和班轮公司供舱量的比较如表3和表4所示.由表3和表4可知: a. 从整个供应链系统的角度考虑,以集中决策作为衡量基准,协调策略使得订舱量与供舱量达到最优,使得货主的需求得到最大的满足.相对而言,分散决策的订舱量与供舱量均未达到最大值.通过数例分析,发现协调策略可以实现预期的目标,消除“双边际效应”. 表3 3种不同供应链系统的利润额Tab.3 Members’ optimal profits in three different kinds of supply chain systems 表4 3种不同供应链系统的订舱量和供舱量Tab.4 Booking quantity and suppy quantity in three different kinds of supply chain systems b. 从供应链各成员角度出发,船代公司与班轮公司在协调策略情况下都达到了最大的订舱量与供舱量,从而实现了自身与供应链整体利润的最大化. c. 在协调策略中,可以发现班轮公司在第二阶段的供舱量为零,即班轮公司根据第一阶段的供舱量以及船代公司的第二次订舱量作出了不生产的决策.这也说明,利用船代公司提供的更新市场信息对需求作出预测,使得其第一阶段供舱量略高于第一阶段船代公司的订舱量,从而降低了生产成本,获得了更大的利润.而船代公司则利用班轮公司给予的两次订货机会,在需求旺盛时期,规避缺货风险,在需求低迷时,利用退货的方式降低风险. 如表5所示,在不同的舱位回购价格b下进行仿真分析,可以发现随着舱位回购价格的增加,会使得船代公司的期望利润和总订舱量也提高,并且使其更趋向于在第一次订舱,减少第二次的订舱量;班轮公司第一次供舱量也因船代公司订舱量的增加而增加,第二次供舱量则变化不大.同时,班轮公司的期望利润随着舱位回购价格的提高而不断下降,而舱位回购价格不仅能增加船代公司的期望利润,而且也可使班轮公司的绩效有所提高,班轮公司的期望利润随着滞销补贴的增加而下降.这种情况下的供应链契约有效消除了供应链成员独立决策时可能出现的双重边际化. 表5 不同回购价格下的协调策略供应链成员的最优决策和利润Tab.5 Supply chain members’ optimal decisions and profits for the coordinated strategy under different return prices 本文考虑动态班轮市场环境下的舱位易逝性特征,研究了船代公司和班轮公司组成的两级供应链决策与协调策略,将3种不同的供应链系统策略进行了对比分析,着重对模型的最优解进行了详细分析,并基于市场信息更新给出了船代公司两阶段最优订购策略和班轮公司两阶段最优生产策略的理论依据和简单方法.研究结果表明:a.供应链分散决策时的船代公司订舱量将小于供应链协调策略时的订舱量,从而证明通过契约激励作用可以消除“双边际效应”,且供销双方和整个供应链系统可以实现利润最大化;b.船代公司所获得的新市场需求信息的多寡将对实现渠道协调时的价格机制产生影响;c.在市场需求信息不对称的情况下,信息对称条件下的价格机制在一定范围内仍可适用. 本文对于动态市场环境下的两级供应链生产和订货决策具有一定指导意义,今后可以从多阶段订货的角度研究班轮公司和船代公司的决策行为,并分析市场需求信息不对称会如何影响供应链各成员的决策. [1] 毛照昉,刘弯弯,李辉.季节性易逝品预售与回购联合决策研究[J].管理科学学报,2016,19(2):74-84. [2] 董坤祥,侯文华,陈宗泽,等.信用期下时滞变质品供应链库存和定价的Stackelberg均衡策略[J].运筹与管理,2015,24(6):76-85. [3] 林晓伟,周熙登.考虑通货膨胀的两层次滞后支付的易逝品订购策略[J].系统管理学报,2015,24(6):912-918. [4] 刘钻石,耿秀丽.面向顾客满意度的服务供应商评价[J].上海理工大学学报,2016,38(6):568-575. [5] 卜祥志,赵辉,武振业,等.基于收益管理的海运集装箱舱位分配随机规划模型[J].系统工程理论方法应用,2005,14(4):330-334. [6] 李冰州,陈旭,武振业.基于收益管理的海运集装箱舱位定价与分配[J].系统工程,2005,23(12):69-73. [7] 王琳,全雄文,杜玉泉.集装箱班轮远期舱位分配博弈研究[J].物流技术,2009,28(4):57-59. [8] LU H A,CHU C W,CHE P Y.Seasonal slot allocation planning for a container liner shipping service[J].Journal of Marine Science and Technology,2010,18(1):84-92. [9] 倪冠群,徐寅峰,徐玖平.航空收益管理价格和座位在线联合控制策略[J].管理科学学报,2014,17(7):10-21. [10] 徐贤浩,余双琪.短生命周期产品的三种库存模型的比较[J].管理科学学报,2007,10(4):9-15,48. [11] 王圣东,周永务.带有二次订购的单制造商多销售商协调模型[J].系统工程学报,2009,24(4):423-429. [12] 尚文芳,祁明,张智勇.基于需求信息更新和短缺量延期供给的易逝品供应链期权契约研究[J].管理学报,2012,9(6):908-912,935. [13] 陈旭.需求信息更新条件下易逝品的批量订货策略[J].管理科学学报,2005,8(5):38-42. [14] KURAWARWALA A A,MATSUO H.Product growth models for medium-term forecasting of short life cycle products[J].Technological Forecasting and Social Change,1998,57(3):169-196. [15] 宋华明,杨慧,罗建强.基于Bayes需求预测更新的供应链合作策略研究[J].管理工程学报,2011,25(2):220-227. [16] CHOI T M,LI D,YAN H M.Quick response policy with Bayesian information updates[J].European Journal of Operational Research,2006,170(3):788-808. [17] OUYANG L Y,WUB K S,HO C H.An integrated vendor-buyer inventory model with quality improvement and lead time reduction[J].International Journal of Production Economics,2007,108(1/2):349-358. [18] 陈金亮,徐渝,贾涛.对称信息下具有需求预测更新的供应链协调模型分析[J].中国管理科学,2005,13(1):37-41. [19] SPENGLER J J.Vertical integration and antitrust policy[J].Journal of Political Economy,1950,58(4):347-352. [20] DONOHUE K L.Efficient supply contracts for fashion goods with forecast updating and two production modes[J].Management Science,2000,46(11):1397-1411. [21] TSAY A A.The quantity flexibility contract and supplier-customer incentives[J].Management Science,1999,45(10):1339-1358. (编辑:丁红艺) Decision and Coordination Strategy for Liner Slots Booking Based on Demand Updating KONG Fanqiang, QU Linchi, XU Lang (SchoolofEconomicsandManagement,ShanghaiMaritimeUniversity,Shanghai201306,China) Considering the difficulty to precisely forecast the demand of consignor,there is large uncertainty in booking shipping slots.The liner company always requires the shipping agency to adopt the strategy of lot booking to protect its own profits.A two-stage profit model was built for the liner company and shipping agency based on the demand information updating of the market.Also,the optimal level of the centralized decision making for the slot supply quantity of the liner company and the booking quantity of the shipping agency was realized.A win-win situation for both the members in the supply chain was achieved by comparing the advantages and profits of centralized and decentralized decision making strategies and by designing an effective slot buy-back contract to coordinate the supply chain.The results by means of different models were illustrated by numerical analysis examples. linershipping;slotsbooking;two-stagedecision;buy-backcontract 1007-6735(2017)03-0255-07 10.13255/j.cnki.jusst.2017.03.009 2017-02-22 国家自然科学基金资助项目(71473162);上海海事大学博士研究生创新项目(2016ycx074) 孔凡强(1981-),男,博士研究生.研究方向:海运与物流产业研究.E-mail:fqkong@126.com 曲林迟(1964-),男,教授.研究方向:港航经济与物流.E-mail:lcqu@shmtu.edu.cn U 695; F 713 A3 模型构建






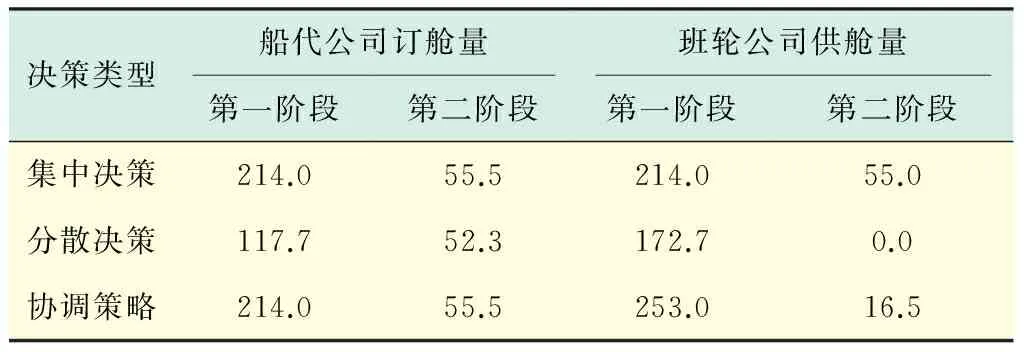
4 算例分析



5 结论

