基于标准化变换的求和法：一种新的样品聚类分析方法

郭春雪，沈 宁，胡良平,2*

(1.军事医学科学院生物医学统计学咨询中心，北京 100850；2.世界中医药学会联合会临床科研统计学专业委员会，北京 100029

基于标准化变换的求和法：一种新的样品聚类分析方法

郭春雪1，沈 宁1，胡良平1,2*

(1.军事医学科学院生物医学统计学咨询中心，北京 100850；2.世界中医药学会联合会临床科研统计学专业委员会，北京 100029

本文目的是介绍一种新的样品聚类分析方法，即基于标准化变换的求和法，它也可归类于传统综合评价方法体系之中。具体地说，第1步，对全部定量变量进行同趋势化变换；第2步，选择一种合适的定量变量标准化变换方法，使第3步中求得的“综合指标”的标准差达到最大值；第3步，求每个样品按综合指标上的数值，即求每个样品在全部标准化变换后的定量指标上取值之和；第4步，将全部样品按综合指标上的取值由大到小(整体为高优指标)或由小到大(整体为低优指标)排序，此顺序就是由优到劣的顺序。基于统计学基础知识和任何两个样品之间易于判定优劣的基本常识，本文提出了评价样品优劣排序合理性的两条标准。以此标准为依据，得出本文方法比其他七种综合评价方法(本质上是样品排序或样品聚类)的排序结果都更为合理。

同趋势化；定量变量标准化变换；传统综合评价；样品排序与分档

1 概 述

1.1 问题的提出

反映一所医院的医疗质量如何，可以请医院管理方面的多位专家提出指标体系，假定这种指标体系由“治愈率”“死亡率”等共10项定量指标组成。假定已随机抽样调查了某地100所三甲医院前述10项定量指标，管理者希望通过分析调查数据结果，将这100所医院划分出优、良、中、差四个档次。请问：①解决这个问题的方法在统计学教科书上被称为什么方法？②这个方法的具体名称叫什么？③若有多种方法可用来回答前面所提出的问题，哪种方法给出的排序与分档结果最为合理？

1.2 对问题的回答

对于前面提出的第1个问题，答案很简单：综合评价[1-2]。意思是：基于10项定量指标在100所医院(注：可将每所医院视为“一个个体”)上的取值，构造出一个“综合评价指标”，它可以被视为10项定量指标的“函数”。于是，将每所医院在10项定量指标上的取值代入综合评价指标表达式，就可以获得其得分值。显然，可将100所医院按得分值由大到小(得分值越大综合评价越好，即整体为高优指标)或由小到大(得分值越小综合评价越好，即整体为低优指标)排序。然后，再借助某种方法(例如：费歇尔的有序样品最优分割法[3-4])将100个有序样品分割成4段或聚成4类。

对于前面提出的第2个问题，答案并不唯一，因为对应的统计分析方法可能有几十种。例如，传统的综合评价方法有：秩和比法、熵值法、Topsis法、模糊聚类分析法等[1-2]；可被间接利用的多元统计分析方法有：主成分分析法、探索性因子分析法、对应分析法和投影寻踪聚类分析法[4-6]。

对于前面提出的第3个问题，答案是否定的。因为迄今为止，尚未见到有关报道。也就是说，到目前为止，尚没有研究提出判别哪种综合评价方法给出的“样品排序”和“样品分档”结果是最合理的。

1.3 新评价方法与判定标准

本文将提出一种新的评价方法，并给出一个判定标准。新方法的全名为“基于标准化变换的求和法”；判定标准为“综合评价指标在全部样品上的得分值的标准差越大，此法评价的结果越合理”。基于此判定标准，经过众多实例分析，发现本文提出的新评价方法在众多评价方法中是最合理的。

2 基于标准化变换的求和法

2.1 何为标准化变换

在对含有多个定量变量的实际问题进行多元统计分析时，为了消除不同变量之间因度量单位和专业含义不同而导致的错误，在统计学教科书中，经常会要求在正式进行多元统计分析之前，先对定量数据进行标准化变换，其目的就是消除各原定量变量单位或量纲对计算结果产生的不利影响。

常用的标准化变换方法有如下两种：其一，某定量变量减去其样本算术平均值再除以其样本标准差；其二，某定量变量减去其样本最小值再除以其样本极差(对高优指标而言)或某定量变量的样本最大值减去该定量变量再除以其样本极差(对低优指标而言)。前述的第二种变换方法常被称为定量变量“归一化处理”[5]。

然而，在SAS/STAT模块的STDIZE过程中，提供了18种对一个定量变量进行标准化变换的方法，其中，最后一种方法是由分析者指定“位置参数(Location)”和“尺度参数(Scale)”条件下的标准化变换，定量变量变换的通用公式为“每个取值减去位置参数值后除以尺度参数值”。各种具体的标准化变换方法详见表1。

表1 在SAS的STDIZE过程中可以实现的标准化变换方法

注：此表摘录自SAS 9.3中SAS/STAT的STDIZE过程的说明文档；“方法”指标准化的具体方法名称；“位置”指进行标准化变换公式中的“位置参数”；“尺度”指进行标准化变换公式中的“尺度参数”

2.2 何为基于标准化变换的求和法

所谓基于标准化变换的求和法，就是对全部定量变量先进行两步预处理，然后进行一步求和运算，最后进行排序运算。具体为：第1步，对全部定量变量进行同趋势化处理，即使全部定量变量都变成高优指标或低优指标。第2步，对全部定量变量进行相同的标准化处理，即对拟参与计算的全部定量变量中都进行相同的标准化变换。第3步，求和运算，即将同一个样品(或观测)上经标准化变换后的全部定量变量的数值相加得到一个合计值(即求和)，此合计值就被当作“综合评价指标”在此样品上的得分值。第4步，排序运算，即将全部样品的得分值由大到小(整体为高优指标)或由小到大(整体为低优指标)排序后编秩，此秩次就标志着各样品的优劣顺序。

2.3 基本思想

因各定量变量有各自的单位和专业含义，必须先对其进行同趋势和标准化变换，使它们具有可加性。每个样品在全部标准化变量上的取值之和，综合了该样品在全部变量上的全部信息，可以近似理解成该样品的“重量”。于是，依据“重量”的数值大小，可以给全部样品进行排序，这就使无序样品变成了有序样品。从而，实现了基于多个定量变量将无序样品转换成有序样品，再基于费歇尔最优分割原理，实现对有序样品的聚类(本质上是分档)分析。本文的研究重点是前一步，最后的分档任务已有现成的SAS程序[4]，可以很方便地实现。

2.4 具体做法

第1步：设共有n个样品，P个定量变量。将全部定量变量同趋势化，即将全部定量变量都转换成高优指标(指标取值越大越好)或低优指标(指标取值越小越好)，通常习惯用高优指标。如何实现同趋势化变换，参见文献[4]。

第2步：从表1中选择一种标准化变换方法，将全部定量变量做相同的标准化变换。

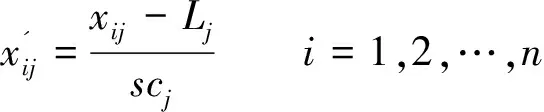
(1)

在式(1)中，Lj为第j个定量变量的位置参数值；scj为第j个定量变量的尺度参数值。

第3步：令Z为全部标准化变换后的综合评价指标，其计算公式见式(2)：

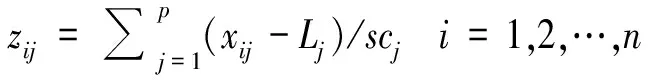
(2)

第4步：将各样品上各定量变量的原始数值代入式(2)求得综合评价指标的得分值。

第5步：将全部样品的得分值由大到小(对高优指标而言)或由小到大(对低优指标而言)排序编上秩次Zr，其原先的样品编号id也随之变动。

3 综合评价质量的判定标准

3.1 为何需要判定标准

依据前面内容可知，传统综合评价方法指的是基于多元定量资料对无序样品进行排序的一系列统计分析方法，其中，最具代表性的方法有：秩和比法、熵值法和Topsis法等。本文所提出的“基于标准化变换的求和法”与前述提及的各种方法大同小异，仍可归属于传统综合评价方法之列。

具有一定统计学基础知识的人都可方便地将三种现代多元统计分析方法(即主成分分析、探索性因子分析、对应分析)引入到传统综合评价方法要解决的问题中来。与此同时，还可引入一种似乎更有数学韵味的多元统计分析方法，即投影寻踪聚类分析法[5-6]。

以上两大类方法可分别被称为“传统综合评价法”与“现代多元统计分析法”，其方法的总数目约十种以上。

问题出现了：采用的综合评价方法不同，常常会得出不同的排序结果。即使采用本文提出的“基于标准化变换的求和法”来计算，当使用者选择表1中18种不同的“标准化方法”，可能其结果也会不尽相同。由此可知，在解决此类问题时，必需给出一个判定标准，用以评价“将无序样品转换成有序样品，进而对它们进行聚类的质量高低”。这里所讲的“质量”很难给出准确的定义或界定，可能还是用“合理性”来度量或评价更贴切一些。

3.2 如何提出判定标准

综上来看，在地铁的网络控制系统设计和应用过程当中，不同环节和部分的科学含量以及使用效率都影响到整体系统的质量，同时关键技术的掌握也代表着一个国家和地区交通事业发展的水平。在我国的地铁建设当中，不断研发具有高新技术的地铁车辆网络系统，是应对城市化进程加快和交通运输压力增大的重要工作。

笔者在现有的文献中，确实没有找到这样一个判定标准。很多发表与“综合评价方法”有关的论文作者都是将自己的排序结果与某个具体方法排序的结果作比较，认为结果基本一致[5,7]。显然，这样的比较方法和得出的结论，难以令人信服。

笔者结合基本常识、统计学基础知识(借鉴投影寻踪聚类分析中关于投影指标函数的构造原理，其内含综合指标的标准差，并通过使该函数达到最大值条件下，获得最大投影方向[5])和任何两个样品间的比较(因为两者之间的比较，很容易得出它们中谁相对更优，例如，用多维尺度分析法分析的原始数据就是基于两样品之间的相似度构造出来的相似度或不相似度矩阵[4])，提出了如下的两条判定标准。

标准1：综合评价指标在全部样品上的得分值的标准差越大，表明它使样品之间的离散度越大，故其聚类的效果就越好。

标准2：对高优指标而言，任何两个样品A与B在同趋势化变换与标准化变换后的全部定量指标上的离差(注意：必须是相同定量指标上的离差)之和大于0，A应位于B之前；反之，则A应位于B之后。

由于“标准2”中涉及“定量变量的标准化运算”，显得不够直观。通常情况下，可以基于同趋势化变换后的原始定量变量直接计算，于是，可将上述“标准2”分解成以下两条。

标准2-1：对高优指标而言，任何两个样品A与B在同趋势化变换后的全部定量指标上的离差(注意：必须是相同定量指标上的离差)之和大于0，A应位于B之前；反之，则A应位于B之后。

标准2-2：对高优指标而言，任何两个样品A与B在同趋势化变换后的全部定量指标上的比值(离差除以四分位间距)之和大于0，A应位于B之前；反之，则A应位于B之后。

说明：标准2稳健性好，但计算繁琐一些；标准2-2稳健性稍差一些，但计算要稍简便一些；而标准2-1稳健性要更差一些，但手工演示极为方便。

4 标准化变换的求和法应用实例

【例1】以文献[5]中“12种不同的水稻插秧密度形式方案”为例，资料见表2。试基于5项经济指标(假定都是高优指标)对12种方案进行综合评价(说明：严格地说，第5项指标“投入费用”应属于低优指标，为了便于与文献上采用投影寻踪聚类分析处理的结果作比较，此处未对其进行倒数变换)。

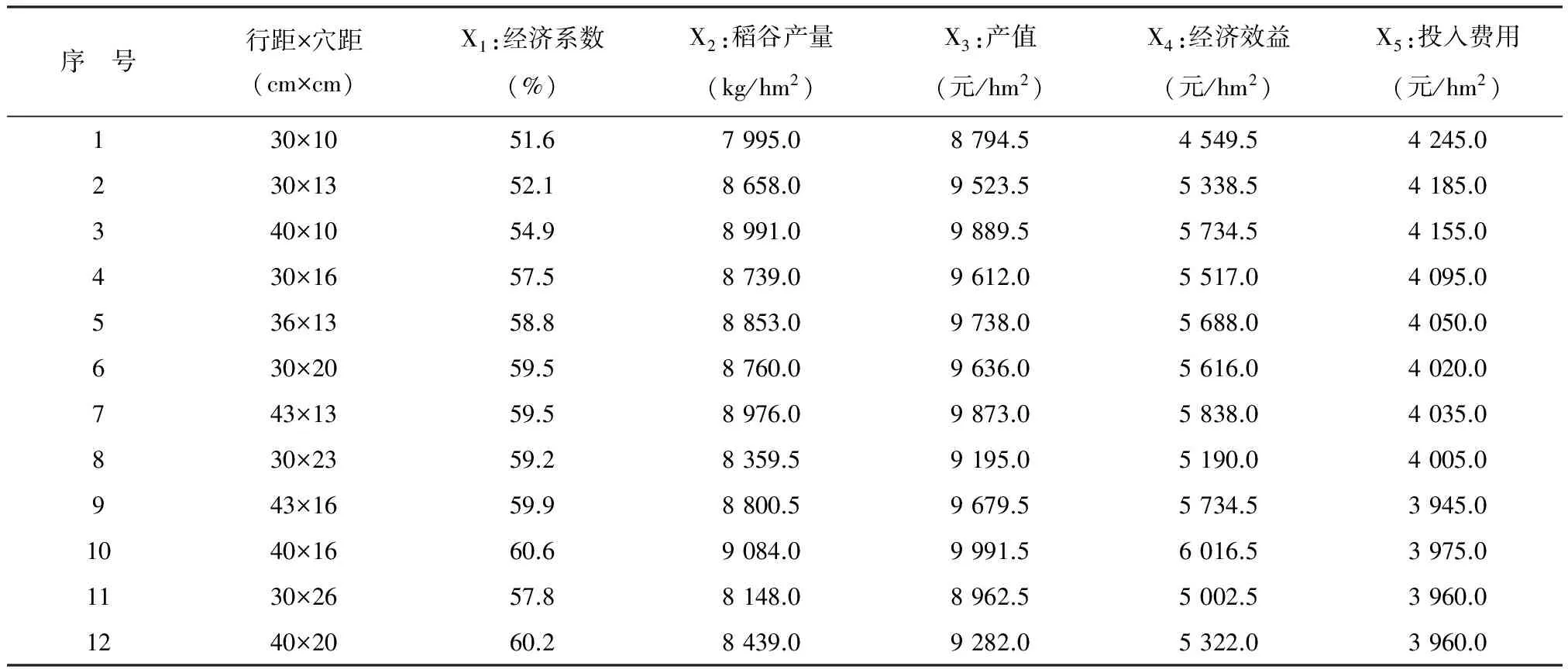
表2 不同密度形式的5项经济指标及其取值

分析与解答：

第1步，对样品进行排序。

采用本文介绍的标准化变换的求和法对表2中的12个样品(即方案)进行排序。利用表1中的前17种标准化变换方法，发现当选择Method=MEAN或Method=MEDIAN两种标准化变换方法时，对应的综合评价指标的标准差取得最大值为1 103.03。此时，对应的输出结果见表3。

在表3中，Z为求得的综合评价指标，Zr为根据Z值由大到小(高优指标)编的秩次，id为资料中原样品的编号，即从优到劣的插秧方案依次为：10>3>7>5>9>6>4>2>12>8>11>1，这些方案的具体密度形式见表2前两列，此处就不详细呈现了。

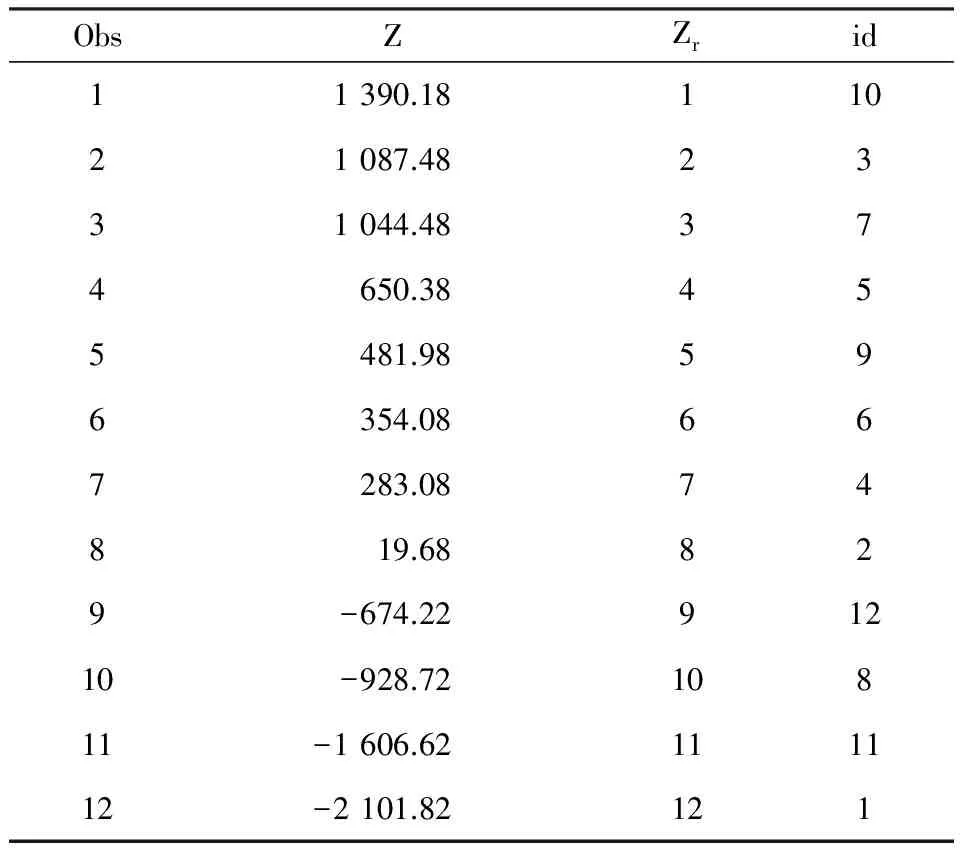
表3 本文方法输出的排序结果

第2步，验证样品排序结果的合理性。

以上算出的12个样品(本例为“插秧方案”)排序结果是否合理呢？基于本文提出的判定标准进行验证。为直观起见，现采用上面的“标准2-1”。

由于各样品均有5个定量指标。现选出其中的第3、5、6、7、9五个样品，它们在5个定量指标上的取值(见表2)如下：

O3=(54.9，8 991.0，9 889.5，5 734.5，4 155.0)

O5=(58.8，8 853.0，9 738.0，5 688.0，4 050.0)

O6=(59.5，8 760.0，9 636.0，5 616.0，4 020.0)

O7=(59.9，8 976.0，9 873.0，5 838.0，4 035.0)

O9=(59.9，8 800.5，9 679.5，5 734.5，3 945.0)。

若按高优指标来看待且按上述标准2-1计算，以上五个样品怎样的排列顺序最合理？

(1)分别计算“样品O3”与“O5、O6、O7和O9”四个样品之间的离差之和：

O3与O5之间对应定量指标上的离差以及和分别为(-3.9，138.0，151.5，46.5，105.0)、437.1；

O3与O6之间对应定量指标上的离差以及和分别为(-5.0，231.5，253.5，118.5，135.0)、733.5；

O3与O7之间对应定量指标上的离差以及和分别为(-5.0，15.0，16.5，-103.5，120.0)、43.0；

O3与O9之间对应定量指标上的离差以及和分别为(-5.0，190.5，210.0，0.0，210.0)、605.5。

以上结果表明：O3应排列在O5、O6、O7和O9之前。

(2)分别计算“样品O5”与“O6、O7和O9”三个样品之间的离差之和：

O5与O6之间对应定量指标上的离差以及和分别为(-0.7，93.0，102.0，72.0，30.0)、296.3；

O5与O7之间对应定量指标上的离差以及和分别为(-1.1，-123.0，-135.0，-150.0，15.0)、-394.1；

O5与O9之间对应定量指标上的离差以及和分别为(-1.1，52.5，58.5，-46.5，105.0)、168.4。

以上结果表明：O5应排列在O6和O9之前，但应排在O7之后，即7>5>(6与9)。

至于O6与O9谁应排列在前面，由O5与O6之间的离差之和296.3>168.4(O5与O9之间的离差之和)可推知，O9应排列在O6之前，即9>6。

总结以上结果可得第3、5、6、7、9五个样品从优到劣的排列顺序应为：3>7>5>9>6。

第3步，给出本文方法以及其他七种综合评价方法对应的综合指标的标准差计算结果。

本文方法秩和比法熵值法Topsis法主成分法探索性因子法对应分析法投影法1103．0301．024348．0310．2561．86410．0260．086

注：“投影法”是“投影寻踪聚类分析法”的简称

第4步，呈现本文方法以及其他七种综合评价方法的排序结果。

本文方法：10>3>7>5>9>6>4>2>12>8>11>1

秩和比法：10>7>3>5>9>6>4>2>12>8>1>11

熵值法：10>7>3>5>9>6>4>2>12>8>11>1

Topsis法：10>7>3>5>9>6>4>2>12>8>11>1

主成分法：10>7>9>5>6>3>4>12>8>2>11>1

因子法：10>3>7>5>9>4>6>2>12>8>11>1

对应法：10>9>7>5>6>3>4>12>8>2>11>1

投影法：10>7>9>5>6>3>12>4>8>11>2>1

在以上8种分析方法对表2中12个样品排序的结果中，熵值法与Topsis法的排序结果完全相同，熵值法与本文方法的标准差较为接近，其对应的排序结果也相当吻合，仅(7>3)与(3>7)不同，其他位置和顺序都完全一样。采用本文介绍的方法，可判定这两种排列顺序何者更合理。

O3=(54.9，8 991.0，9 889.5，5 734.5，4 155.0)

O7=(59.9，8 976.0，9 873.0，5 838.0，4 035.0)

若按高优指标来看待且按本文中的标准2-1计算，以上两个样品怎样的排列顺序最合理？

计算这两个样品之间的离差之和。O3与O7之间对应定量指标上的离差以及和分别为(-5.0，15.0，16.5，-103.5，120.0)、43.0。说明O3应位于O7之前，即应取(3>7)的顺序，也即本文方法比熵值法和Topsis法的排序结果更合理。

【例2】某研究者收集了9个地区单位及每个单位对应的12个指标，即农业生产力综合指标评价体系。具体资料见表4。研究者要对南京地区(5县4区)农业生产力进行优劣评价[7]。

表4 农业生产力评级指标样本集

注：该12个评价指标皆为高优指标

分析与解答：

第1步，对样品进行排序。

采用本文介绍的标准化变换的求和法对样品进行排序，利用表1中的前17种标准化变换方法，发现当选择Method=MEAN标准化变换方法时，对应的综合评价指标的标准差取得最大值为2.375 116 4。此时，对应的输出结果见表5。

表5 本文方法输出的排序结果

在表5中，Z为求得的综合评价指标，Zr为根据Z值由大到小(高优指标)编的秩次，id为资料中原样品的编号，即9个地区单位从优到劣的农业生产力依次为：3>9>5>1>8>6>4>7>2。

第2步，给出本文方法以及其他七种综合评价方法对应的综合指标的标准差计算结果。

第3步，本文方法以及其他七种综合评价方法的排序结果。

本文方法：3>9>5>1>8>6>4>7>2

秩和比法：3>9>5>1>8>4>6>7>2

熵值法：3>9>5>6>8>1>7>4>2

Topsis法：3>9>5>1>8>6>7>4>2

主成分法：9>3>1>4>5>8>7>6>2

因子法：3>7>6>5>4>9>8>1>2

对应法：9>5>7>8>4>3>1>6>2

投影法：3>9>5>8>1>4>6>7>2

以上8种分析方法对9个样品排序的结果中，熵值法与Topsis法的排序结果完全相同，主成分分析法与本文方法的标准差较为接近，但排序结果偏差较大，采用本文介绍的方法进行验算，可发现本文方法更合理一些，即农业生产力由好到差的单位依次为：江宁县>雨花区>高淳县>六合县>栖霞区>浦口区>溧水县>大厂区>江浦县。

本文方法秩和比法熵值法Topsis法主成分法探索性因子法对应分析法投影法2．3751．6700．1510．1292．16010．0260．803

注：“投影法”是“投影寻踪聚类分析法”的简称

说明：因篇幅所限，对例2中各种方法排序结果的合理性未做详细验证。感兴趣的读者可借助本文提出的标准进行验证。

笔者真诚希望广大读者提出宝贵的意见和建议，盼望读者能提出更加科学、严谨的综合评价方法和判定排序合理性的标准。

[1] 孙振球. 医学统计学[M]. 北京：人民卫生出版社，2002：373-396.

[2] 苏颀龄. 中国医学统计百科全书：统计管理与健康统计分册[M]. 北京：人民卫生出版社，2004：30-94.

[3] 茆诗松. 统计手册[M]. 北京：科学出版社，2006：556-559.

[4] 胡良平. 科研设计与统计分析[M]. 北京：军事医学科学出版社，2012：472-479，597-650.

[5] 付强，赵小勇. 投影寻踪模型原理及其应用[M]. 北京：科学出版社，2006：46-119.

[6] 田铮，林伟. 投影寻踪方法与应用[M]. 西安：西北工业大学出版社，2008：13-90.

[7] 黄勇辉，朱金福. 基于加速遗传算法的投影寻踪聚类评价模型研究与应用[J]. 系统工程，2009，27(11): 107-110.

(本文编辑：吴俊林)

Summing method based on a standardized transformation: a new sample clustering methodology

GuoChunxue1,ShenNing1,HuLiangping1,2*

(1.ConsultingCenterofBiomedicalStatistics,AcademyofMilitaryMedicalSciences,Beijing100850,China； 2.SpecialtyCommitteeofClinicalScientificResearchStatisticsofWorldFederationofChineseMedicineSocieties,Beijing100029,China*Correspondingauthor:HuLiangping,E-mail:lphu812@sina.com)

This article aims to introduce a new method for the sample clustering analysis, entitled the summing method based on a standardized transformation, which can also be categorized into the traditional method system of the generalizing comprehensive evaluation. Briefly speaking as follows: step 1, all the quantitative variables are transformed with the same trend; step 2, select a suitable quantitative variable normalization method, so that the standard deviation of the "comprehensive index" to reach the maximum in the next step; step 3, find the value of each sample on the comprehensive index, that is, find the summation of the standardized values of the quantitative indices of all the samples; step 4, sequence all the samples in accordance with the numeric size of the comprehensive indicators from large to small (the entire indicators considered to be high priority index) or from small to large (the entire indicators considered to be low priority index), and this sequence indicates the order from superiority to the inferiority. On the basis of the statistical knowledge and the common knowledge of pointing the bigger one between 2 values, this article raises 2 criteria for evaluating the sequence rules. Based on this standard, we conclude that this new method is superior to the other 7 methods of the comprehensive evaluation which are essentially for sample sorting or sample clustering.

Transform with the same trend; Quantitative variable normalization method; Traditional comprehensive evaluation method; Sample sorting and bracketing

R195.1

A

10.11886/j.issn.1007-3256.2017.03.003

国家高技术研究发展计划课题资助(2015AA020102)

2017-06-04)

*通信作者：胡良平，E-mail：lphu812@sina.com)