试验设计类型之可以考察部分交互作用的多因素设计：正交设计与均匀设计

张效嘉，胡良平,2*

(1.军事医学科学院生物医学统计学咨询中心，北京 100850； 2.世界中医药学会联合会临床科研统计学专业委员会，北京 100029

试验设计类型之可以考察部分交互作用的多因素设计：正交设计与均匀设计

张效嘉1，胡良平1,2*

(1.军事医学科学院生物医学统计学咨询中心，北京 100850； 2.世界中医药学会联合会临床科研统计学专业委员会，北京 100029

本文旨在介绍两种多因素试验设计方法，即正交设计与均匀设计。由于析因设计中的试验点数目过多，在既要较少试验点数目，又要能比较准确地揭示多因素对评价指标影响规律的要求之下，宜选择正交设计或均匀设计。正交设计具有“试验点均匀分散、整齐可比且可以事先安排少数交互作用项”的特点，因此，结果的可信度较高，只需采用方差分析处理定量资料；均匀设计具有“试验点极其均匀分散、正交性在一定程度上受到破坏，不能事先安排交互作用项”的特点，因此，允许很少数目的试验点，但需采用多重回归分析处理资料且分析结果不唯一。

析因设计；分式析因设计；正交设计；均匀设计；试验点

1 概 述

在此文之前所介绍的各种试验设计类型一般都

以“纵”与“横”两个方向来呈现因素及其水平，例如，下面的表1就呈现了一个三因素析因设计的“架构”。

表1 三个试验因素作用下OD值的测定结果

在表1中，A、B两个因素被放置在表的左侧表头，其具体水平被放置在表身左侧并位于六个横行上；而C因素及其水平都被放置在表头短横线下方。于是根据“纵、横”交叉处的数据，就知道它们产生于什么样的“试验条件”。例如，开始的两个数据“0.39、0.41”，它们位于第1行与“第1列和第2列”交叉处。表明这两个试验数据所对应的试验条件为“A1、B1、C1”，即三个试验因素都分别取各自的一水平，两个数据是同一个试验条件下的两次独立重复试验结果。同理可知，最后两个数据“0.35、0.37”所对应的试验条件为“A2、B3、C4”，即A、B、C三个试验因素分别取“二水平”“三水平”与“四水平”条件下的两次独立重复试验结果。

现在考虑这样的问题：若某试验要涉及10个因素，还采取表1的方式来呈现因素及其水平组合，如何制表呢？

对上面的问题，人们感到十分棘手，仍采用“纵、横”交叉的手法很难操作。于是干脆“化繁为简”，将所有因素都放置在表头上，表身处放置各因素的水平，每一横行上放置全部因素的一个特定水平组合(即一个特定的试验条件或试验点)。基于这种想法，改写表1，见表2。

表2 表1变形的结果

显然，用表2的方式呈现因素及其水平组合是很方便的，而且，可以允许任何数目的因素，因素的水平数也不受任何限制。

现在再来考虑这样的问题：当试验中涉及的试验因素数目很多时，其水平组合数就非常之多，如何既能以较少种类的组合数安排试验，又不至于导致“多因素非平衡组合试验”[1]这种不科学安排的出现？

对上述问题的回答是：可以采取分式析因设计、正交设计、均匀设计、组合设计和最优设计等[2-7]。

2 正交设计简介

2.1 概念简介

在表2的前三列和第六、七、八列中，共有24种水平组合(即24行)。这三列之间有什么规律呢？同一因素不同水平出现的次数相等；任何两因素之间不同“有序数对”出现的次数相同。如果我们让A、B、C三个因素都取3个水平，将其全部27种水平组合都按表2的方式呈现出来，此时，三个因素对应的三列就满足如下的两个规律：①任何一列中不同水平出现的次数相同；②任何两列不同“有序数对”出现的次数相同。

在数学上，称满足以上两条规律的数据阵列具有“正交性”，其几何解释就是三个向量在空间互相垂直。所谓正交设计，就是找出一系列相互正交的向量组成一个“设计矩阵”，其每一行就是全部因素水平的一种特定组合。每种组合相当于科研人员所说的“一个试验组”，通常，各组必须做m次独立重复试验。

需要弄清一个问题：同水平的K因素析因设计，在本质上，就是K因素正交设计。那么，正交设计是否就是“多余的”了？事实上，研究者打算选用正交设计来安排多因素试验，一个最主要的原因就是希望少做一些“试验点”，而不是用析因设计(包含因素的全部水平组合)的另一种呈现方式。也就是说，正交设计中的试验点可以是同水平析因设计中的全部试验点，也可以是从中抽出的一部分试验点(但它们必须满足正交性要求)。比相同规模(指因素的个数和水平数)的析因设计少了部分试验点的正交设计，既不是“分式析因设计[4]”和“含区组因素的析因设计[1]”，也不是“多因素非平衡组合试验[1]”，而是基于某种“数学根据”决定的全部因素的部分水平组合。在实际使用时，研究者只需要选择数学家编制好的各种规格化的正交表[2-3]即可。基于正交性要求挑选出来的试验点具有如下特点：均匀分散、整齐可比。

2.2 实例简介

【例1】在乙酰苯胺磺化工艺的研究中，有4个因素：反应温度(℃)A、反应时间(h)B、磺酸浓度(%)C、操作方法D，各取两水平，试验的结果为产物的“收率(%)”。试验目的：希望弄清各因素在怎样的搭配条件下收率最高。已知反应温度与反应时间之间的交互作用不可忽视，各试验条件下不必进行重复试验，希望总试验次数尽可能少一些，请给出合适的试验设计方案。4个试验因素的水平分别如下。

因素名称(单位)1水平2水平反应温度(℃)5070反应时间(h)12磺酸浓度(%)1727操作方法搅拌不搅拌

【具体设计】若选择析因设计，不同的试验条件数为24=16种，各试验条件下至少要做2次独立重复试验，总试验次数至少为32次，不符合题意要求。某研究者给出了如下的8种试验条件，即8个试验组。

组 别各组的具体条件组合情况第1组：反应温度取50℃、反应时间取1h、磺酸浓度取17%、搅拌第2组：反应温度取50℃、反应时间取1h、磺酸浓度取27%、不搅拌第3组：反应温度取50℃、反应时间取2h、磺酸浓度取17%、不搅拌第4组：反应温度取50℃、反应时间取2h、磺酸浓度取27%、搅拌第5组：反应温度取70℃、反应时间取1h、磺酸浓度取17%、不搅拌第6组：反应温度取70℃、反应时间取1h、磺酸浓度取27%、搅拌第7组：反应温度取70℃、反应时间取2h、磺酸浓度取17%、搅拌第8组：反应温度取70℃、反应时间取2h、磺酸浓度取27%、不搅拌

【对设计类型的判定】从表面上看，这个试验涉及一个因素，它叫做“组别”。但从各组的具体条件来看，它确实涉及四个因素，分别为“反应温度”“反应时间”“磺酸浓度”和“搅拌方法”。每个因素都取2个水平，若将这四个因素的水平全面组合，共有16种，现在只做了其中一半组合条件下的试验，称为总试验条件数的二分之一实施。

事实上，前面的安排对应着如下的设计：

选择L8(27)正交表，因为该正交表的自由度为7，比所需要的自由度5多2个自由度，即正交表中将有两个空列，可用于估计试验误差。此时，只需要做8种试验组合(若不做重复试验，总试验次数也是8)，就可以满足研究者的要求。

设因素A为反应温度(℃)、因素B为反应时间(h)、因素C为磺酸浓度(%)、因素D为操作方法。选用L8(27)正交表，将A放在第1列、B放在第2列、查找L8(27)正交表的交互作用表，得交互作用A×B应落在第3列上，于是，可把C放在第4列，D可以放在5、6、7三列中任何一列上，不妨将D放在第7列上，见表3。

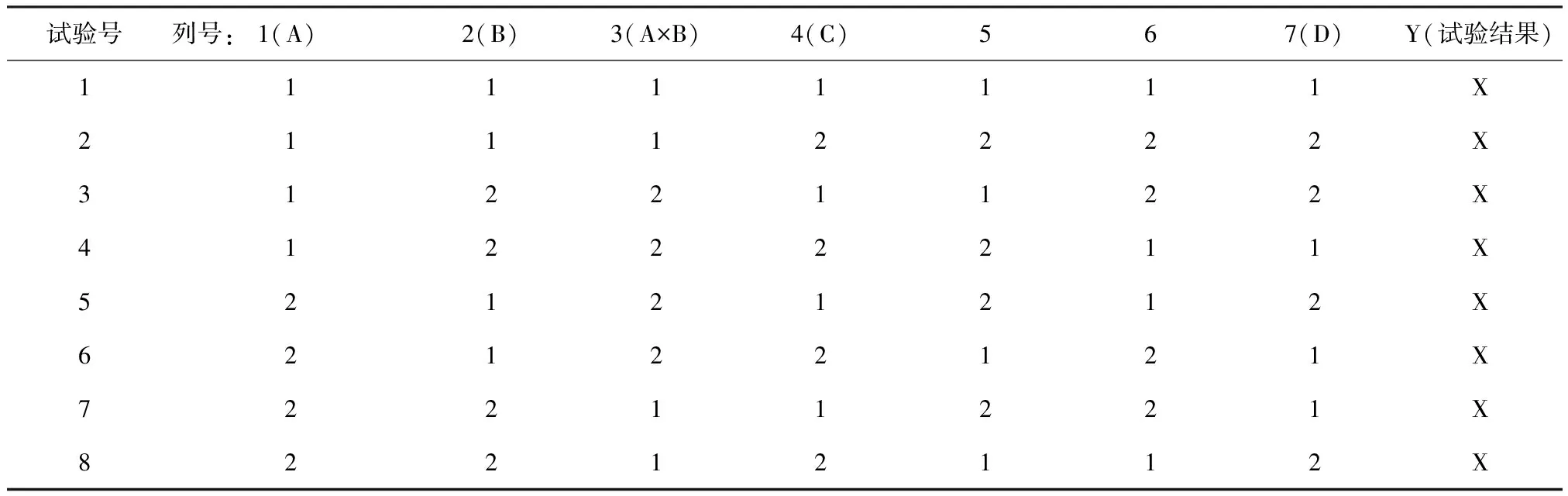
表3 L8(27)正交表

根据表3并不便于进行试验，最好将该表中第1、2、4、7列抽出来，以使表格简化，不易看串行，不仅如此，还应将该表中的“代码水平”转化成“试验因素的真实水平”，这样，进行试验时才不会出错。结果见表4，当试验结束后将试验结果填入此表中最后一列。

表4 用L8(27)正交表安排4个试验因素

注：基于正交表中各行上的试验条件做试验时，一般每行上都至少要做两次独立重复试验，特别是以生物体(例如某种动物)为受试对象时，评价指标的变异度很大，必需做足够次数的独立重复试验

3 均匀设计简介

3.1 概念简介

有了以上关于正交设计的基本概念后，再来谈均匀设计就很容易了。与正交设计类似，基于均匀性要求挑选出来的试验点具有如下特点：试验点在空间尽可能“均匀分散”，必要时，可能会部分地牺牲掉“正交性”。也就是说，产生于均匀设计的定量数据可能不具有“整齐可比性”了。因此，可以用方差分析处理来自正交设计一元定量资料，而需要采用多重回归分析方法处理来自均匀设计一元定量资料。

在实际使用时，研究者只需选择数学家编制好的各种规格化的均匀设计表和与之对应的交互作用表即可[1-2]。

3.2 实例简介

【例2】某研究者用均匀设计方法完成的分析化学方面的研究报告，其题目是“高效毛细管电泳分离的优化策略”。该文提出一种新的优化策略，综合分析“A：表面活性剂浓度”“B：缓冲溶液pH值”“C：磷酸盐缓冲溶液浓度”“D：有机添加剂浓度”及“E：操作电压”5个定量的试验因素对高效毛细管电泳分离的影响，用多种优化目标函数考察分离度和峰分布均匀性。5个试验因素拟取的水平如下。设计时无法考虑因素之间的交互作用，还希望试验次数尽可能少，试选择合适的设计方案安排此试验。

A(表面活性剂浓度的水平)：1020304050607080B(缓冲溶液pH值的水平)：7．517．757．928．138．368．718．939．06C(磷酸盐缓冲溶液浓度的水平)：1520253035404550D(有机添加剂浓度的水平)：036912151821E(操作电压的水平)：15．015．516．016．517．017．518．018．5

【具体设计】采用U8(85)均匀设计表安排试验，见表5。

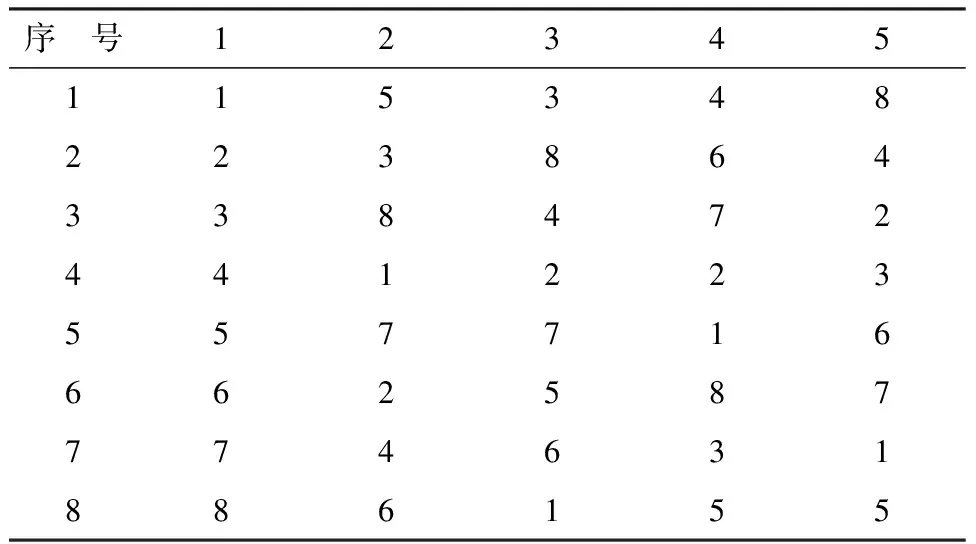
表5 U8(85)均匀设计表

用5个试验因素的具体水平取代表5中的代码水平，并记录各次试验结果(暂用“X”表示)，见表6。

4 正交设计与均匀设计异同点归纳

4.1 相同点

4.1.1 设计表

在很多场合下，两种设计都有很多可供直接选用的规格化的设计表(即正交表及其交互作用表；均匀表及其交互作用表)。

4.1.2 试验点

两种设计中所确定的试验点都是从相应规模的析因设计所有试验点中挑选出来的一部分试验点。

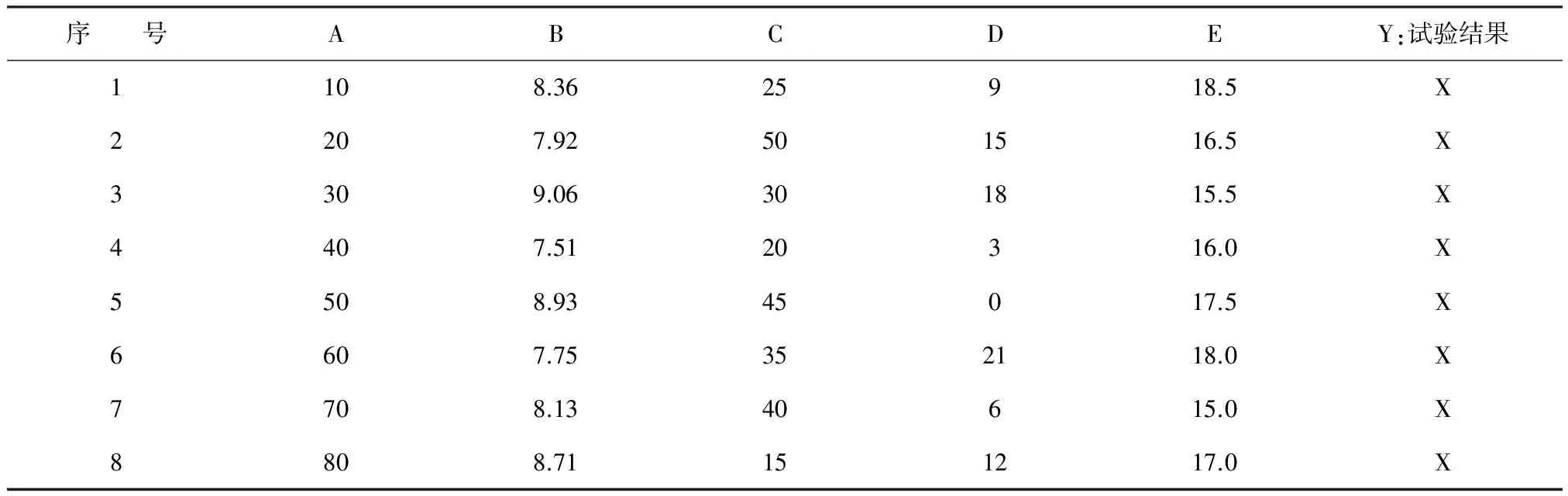
表6 用U8(85)安排5种巴比妥类药物MEKC分离条件优化试验

注：基于均匀表中各行上的试验条件做试验时，一般每行上都至少要做两次独立重复试验，特别是以生物体(例如某种动物)为受试对象时，评价指标的变异度很大，必需做足够次数的独立重复试验

4.1.3 设计方案

两种设计的设计方案都以“列”的形式呈现全部拟考察因素，以“行”的形式呈现各试验点(即因素的特定水平组合)。

4.1.4 水平数

在绝大多数场合下，两种设计都更倾向于安排同水平的试验研究问题(少数场合下，有混合水平的)。

4.2 不同点

4.2.1 抽取试验点所依据的要求不同

正交设计依据“正交性”抽取试验点；而均匀设计依据“均匀性”抽取试验点。

4.2.2 具有的特点不同

正交设计具有“试验点均匀分散、整齐可比且可以事先安排部分交互作用项”的特点，另外，可用方差分析处理产生于正交设计的定量资料；而均匀设计具有“试验点极其均匀分散、正交性受到一定程度的破坏且不能事先安排交互作用项”的特点，另外，需要用多重回归分析处理产生于均匀设计的定量资料。

4.2.3 同水平不同型号的设计表之间试验点数目变化规律不同

当因素的水平数确定下来后，不同型号的正交表中的试验点数目之间按水平数相乘的规律变化，例如，在2水平正交表[L4(23)、L8(27)、L16(215)、L32(231)、L64(263)、L128(2127)]中，每相邻(指“型号”，下同)两张正交表所包含的试验点数目之间呈2倍的关系(见前面符号中“L”的下角标数字)。在3水平正交表[L9(34)、L27(313)、L81(340)、L243(3121)]中，每相邻两张3水平正交表的试验点数目之间呈3倍的关系(见前面符号中“L”的下角标数字)。同理，在4水平正交表中，每相邻两张4水平正交表的试验点数目之间呈4倍的关系。

然而，对均匀设计表而言，每相邻两张3水平均匀表的试验点数目之间相差3、每相邻两张4水平均匀表的试验点数目之间相差4。同水平的均匀表比较多见，2水平的均匀表就是2水平的正交表，其他同水平的均匀表中常用的如下[2]。

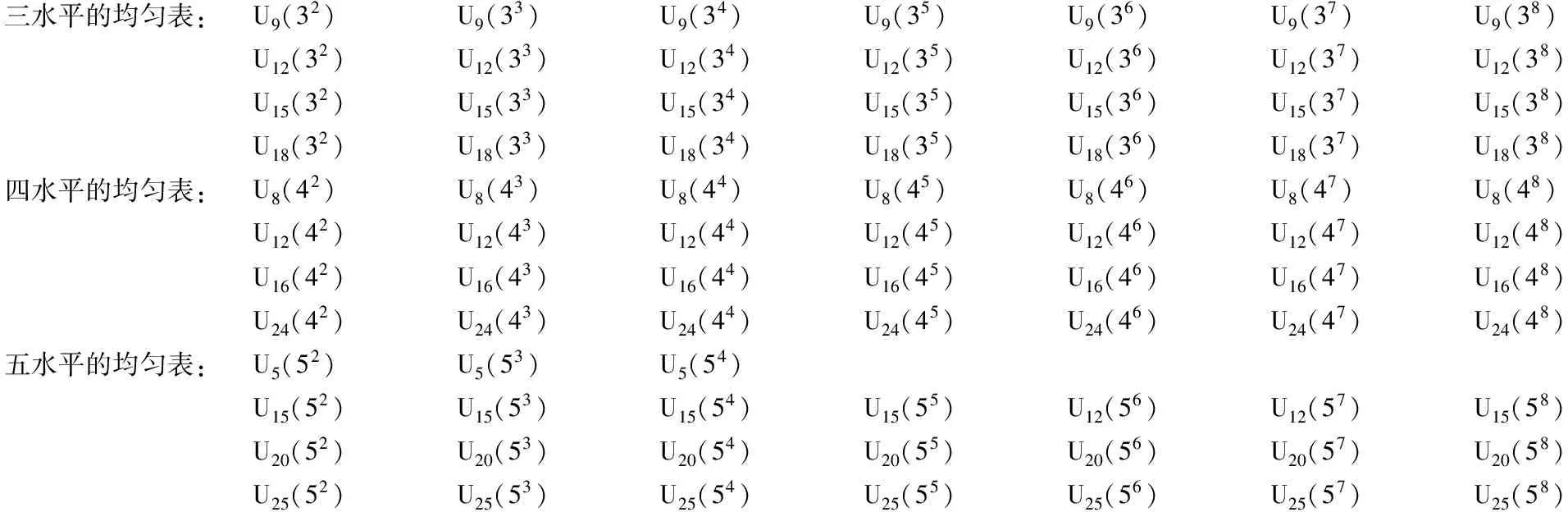
三水平的均匀表：U9(32)U9(33)U9(34)U9(35)U9(36)U9(37)U9(38)U12(32)U12(33)U12(34)U12(35)U12(36)U12(37)U12(38)U15(32)U15(33)U15(34)U15(35)U15(36)U15(37)U15(38)U18(32)U18(33)U18(34)U18(35)U18(36)U18(37)U18(38)四水平的均匀表：U8(42)U8(43)U8(44)U8(45)U8(46)U8(47)U8(48)U12(42)U12(43)U12(44)U12(45)U12(46)U12(47)U12(48)U16(42)U16(43)U16(44)U16(45)U16(46)U16(47)U16(48)U24(42)U24(43)U24(44)U24(45)U24(46)U24(47)U24(48)五水平的均匀表：U5(52)U5(53)U5(54)U15(52)U15(53)U15(54)U15(55)U12(56)U12(57)U15(58)U20(52)U20(53)U20(54)U20(55)U20(56)U20(57)U20(58)U25(52)U25(53)U25(54)U25(55)U25(56)U25(57)U25(58)

Un(Pq)符号的含义是：“U”代表均匀(Uniform)之意；“n”代表均匀表的行数或试验因素的不同水平组合数，即不同的试验点数；“P”代表试验因素的水平数，即各列中不同的水平代码数；“q”代表均匀表的列数，即最多可安排的试验因素个数。

[1] 胡良平. 统计学三型理论在实验设计中的应用[M]. 北京：人民军医出版社，2006：133-138，152-163.

[2] 方开泰，马长兴. 正交与均匀试验设计[M]. 北京：科学出版社，2001：35-211.

[3] 姬振豫. 正交设计的方法与理论[M]. 香港：世界科技出版社，2001：1-97.

[4] Dean A, Voss D. Design and analysis of experiments[M]. New York: Springer, 1999: 483-546.

[5] 任露泉. 试验优化设计与分析[M]. 2版. 北京：高等教育出版社，2003：10-399.

[6] 王万中. 试验的设计与分析[M]. 北京：高等教育出版社，2004：114-357.

[7] 茆诗松, 周纪芗, 陈颖. 试验设计[M]. 北京：中国统计出版社，2004：117-366.

(本文编辑：吴俊林)

欢迎订购《精神疾病案例诊疗思路》(第三版)

由《四川精神卫生》杂志副主编、新乡医学院第二附属医院(河南省精神卫生中心)杨世昌教授主编，中南大学精神卫生研究所张亚林教授主审的《精神疾病案例诊疗思路》(第三版)(ISBN 978-7-117-24357-5/R·24358)由人民卫生出版社2017年6月份出版。

为确保本次修订质量，编委由来自上海交大医学院附属精神卫生中心、南京医科大学、沈阳市精神卫生中心、四川省精神卫生中心、广东医科大学附属深圳第六人民医院、广西壮族自治区精神卫生中心、贵州省人民医院、华中科技大学同济医学院附属精神病医院、深圳市精神卫生中心，河北省精神卫生中心、新疆自治区人民医院、河南科技大学第五附属医院、新乡医学院第二附属医院等单位从事临床与教学工作的同道们组成。

该修订版共计92.5万字，本书紧密结合临床诊疗思维，通过对真实病例接诊的整个环节介绍，展示精神疾病的诊疗思维。本次修订有以下三个方面。第一，介绍精神疾病的诊断学基础——晤谈技术、病史采集、精神状况检查以及精神疾病的诊断思维。第二，典型案例篇，根据临床实践中典型病例的病情变化提供病情或临床相关信息，进而提出问题，并分析诊疗思路。第三，本次修订增加了临床诊疗的影响因素(法律、医保、医患关系、医学模式等)以及循证医学与临床决策等相关章节，同时增加了拓展思路的案例，该部分的案例均源于临床疑难病历讨论的真实案例，在“提问式分析”基础上，提出开放性问题，为读者留下思考的空间。

Types of the multifactor experimental designs with partial interactions: orthogonal and uniform design

ZhangXiaojia1,HuLiangping1,2*

(1.ConsultingCenterofBiomedicalStatistics,AcademyofMilitaryMedicalSciences,Beijing100850,China； 2.SpecialtyCommitteeofClinicalScientificResearchStatisticsofWorldFederationofChineseMedicineSocieties,Beijing100029,China*Correspondingauthor:HuLiangping,E-mail:lphu812@sina.com)

The paper aims to introduce two multifactor experimental designs: orthogonal design and uniform design. Excessive experimental points are required in factorial design, that may be its limitations. Orthogonal design and uniform design are frequently applied, because less experimental points are required in these designs. Additionally, they may demonstrate the effects of experimental factors on evaluation index accurately. Orthogonal design is characterized by uniform dispersion and regularly-comparable experimental points. Additionally, it may arrange partial interactions in advance. Consequently, analysis of variance may be applied to analyze data from Orthogonal design and the results are reliable. Experimental points in uniform design are extremely uniformly distributed at the cost of reduce orthogonality. Uniform design may not arrange interactions in advance. Consequently, multiple regression analysis may be utilized to analyze data from uniform design, and the results may be various.

Factorial design; Fractional factorial design; Orthogonal design; Uniform design; Experimental point

R195.1

A

10.11886/j.issn.1007-3256.2017.03.002

国家高技术研究发展计划课题资助(2015AA020102)

2017-06-04)

*通信作者：胡良平，E-mail：lphu812@sina.com)