化工过程非方瘦系统的串级控制系统结构设计
许锋,袁未未,罗雄麟
(中国石油大学(北京)自动化系,北京 102249)
化工过程非方瘦系统的串级控制系统结构设计
许锋,袁未未,罗雄麟
(中国石油大学(北京)自动化系,北京 102249)
化工过程一般为多变量系统,其中输出变量个数多于输入变量个数的非方多变量系统称为瘦系统,现有的非方系统控制结构设计一般采用方形化处理方法,只能形成一个输入变量与一个输出变量配对的单回路控制,要么作为工艺控制指标的重要变量不能成为被控变量,要么次要变量未纳入反馈控制,无法满足控制要求。本文介绍了非方系统的平均频域相对增益阵,对瘦系统进行了变量配对分析,提出了一种瘦系统串级控制系统结构设计方法。这种方法在不添加输入变量的同时有效利用了所有的输出变量反馈,使系统反馈信息更完备,构造了重要变量与次要变量结合的串级控制系统。最后通过实例分析说明了瘦系统的串级控制系统结构设计方法不仅能够得到合理的变量配对,而且系统控制性能良好,尤其在进行干扰抑制的过程中体现出了快速性和高效性。
过程控制;过程系统;多变量系统;瘦系统;关联分析;变量配对;串级控制系统
引 言
分散PID控制器广泛应用于多变量系统[1-5],虽然随着控制理论的发展,多变量系统开始使用先进控制算法进行控制系统设计,特别是模型预测控制,但是先进控制往往设计复杂,难以实现,不易维护,并且现场工程师对先进控制的熟悉程度也不高,因此考虑到底层控制系统安全可靠的要求,工业现场的底层控制系统主要采用的仍然是常规PID控制。
多变量系统一般都存在变量间的相互关联,使得闭环系统的控制性能降低[6],因此控制回路设计时首先要对系统进行关联分析以及变量配对,使得各回路间的相互作用降到最低,然后再将该系统看作多个单入单出(single-input single-output,SISO)系统,并运用SISO理论进行控制器设计[7]。多变量系统的关联分析和变量配对方法中,目前应用最广泛的即为Bristol提出的相对增益阵[8](relative gain array,RGA)法和由之发展而来的相关方法。最早提出的 RGA方法只利用了系统的静态信息,因此在一些情况下变量配对并不是很准确。对此,McAvoy等[9-10]提出了动态相对增益阵(dynamic relative gain array, DRGA),Gagnepain 等[11]提出基于开环阶跃响应的平均动态增益(average relative gain array, ARGA),Tung等[12]提出相对动态增益矩阵(relative dynamic gain array, RDGA),He等[13]提出了相对正则化增益阵(relative normalized gain array, RNGA),Xiong等[14]提出了有效相对增益阵(effective relative gain array, ERGA),罗雄麟等[15]提出了动态相对增益阵(dynamic-relative gain array,dynamic-RGA),任丽红等[16]结合稳态和动态信息提出了相对能量增益阵(relative energy gain array,REGA)。RNGA利用对象的单位阶跃响应获得动态信息,采用误差积分指标来评价过程的动态特性,因此在系统出现衰减振荡而使正负偏差相抵时,可能会出现不合理配对,并且RNGA没有考虑到平均停留时间(average residence time)时滞后对系统变量配对的影响,因此这种方法不适用于大滞后过程。ERGA是频域上的一种选择方法,需要通过截止频率计算,当分别选择相角穿越频率和带宽频率作为截止频率时,可能会出现不同配对结果。REGA通过定义能量消耗大小来表示系统的动态特性,采用平方误差积分指标来评价过程的动态特性,这种方法适用于多变量时滞系统,弥补了RNGA的缺点,相对而言,使配对更为准确。RGA也被推广到不确定多变量系统[17-22]中,Yu等[23]通过RGA对系统的鲁棒性进行分析。许锋等[24]提出相对频率增益阵,在处理大纯滞后过程、积分过程以及不稳定过程等时具有较大优势。
随着流程工业的发展,生产过程中越来越多出现高维多变量系统,并且经常出现输入与输出维数不相等的非方系统。Chang等[25]将 RGA推广到非方系统中得到非方相对增益(non-square relative gain array, NRGA),Skogestad等[26]总结了 NRGA的性质,任丽红等[27]基于REGA提出了非方相对能量增益矩阵(non-square relative energy gain array,NREGA)方法。目前对非方系统的控制系统设计,一般通过增加或减少输入输出变量的个数,将非方系统转化为方系统,再进行控制结构设计。然而在进行系统方形化时,加入非必要的输出变量或输入变量会使成本增加,减少输出变量会使系统的反馈信息变少,而减少输入变量又会降低系统的可操控性。因此,如果直接在非方系统上设计分散PID控制系统将比在方化后的系统上进行设计更加可取,并且在某些简单控制系统无法满足系统的控制性能要求,同时又没有必要运用先进控制系统的情况下,设计复杂控制系统最为合适。
本研究提出一种适用于非方系统的平均频域相对增益阵,称作平均频域 NRGA。基于 RGA、NRGA和平均频域NRGA,针对输出变量多于输入变量的非方系统,也称为瘦系统,提出了一种新的控制结构设计方法,利用上述关联分析工具对瘦系统进行变量分析和配对,实现串级控制系统结构设计,大大提高了控制速度,并且控制性能良好。
1 平均频域NRGA
1.1 平均频域NRGA的定义
假设多输入多输出系统的传递函数矩阵为
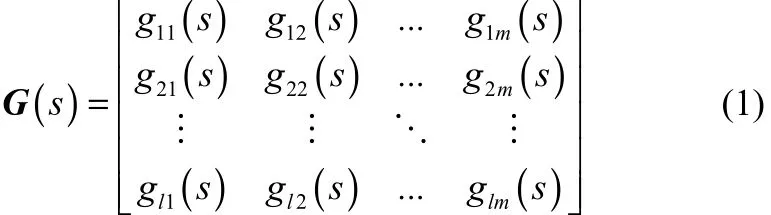
其中,当l≠m时系统即为非方系统。将时域NRGA推广到频域,得到频域NRGA为

其中,Λ(ω)表示 G(s)的频域 NRGA,G+(jω)表示 G(s)的伪逆,⊗表示Schur乘积,即相同位置的元素相乘。因为Λ(ω)为频率ω的函数,将Λ(ω)对频率ω取积分均值,可以得到平均频域NRGA

式(3)中,积分下限ω0的取值为0,积分上限ωn一般取截止频率。
与NRGA相比,平均频域NRGA考虑了系统的动态特性,在选择响应速度快的变量时具有很大的优势。
1.2 平均频域NRGA的性质
Skogesta等[26]提出,当系统G(s)为l×m维时,利用奇异值分解(SVD)将其分解为G=UΣVH,其中U为GGH特征向量组成的矩阵,V为GHG特征向量组成的矩阵,由于有r=rank(G)≤min(l, m)个非零奇异值,并且只有非零奇异值对总体结果才有贡献,因此 G的 SVD可以写成简化型 SVD,即其中Ur是矩阵U的前r列,包含了G的前r个输出奇异向量,Vr是矩阵V的前r列,包含了G的前r个输入奇异向量。
平均频域NRGA基于NRGA和平均频域RGA提出,因此具有和NRGA及平均频域RGA相似的性质[24-26]:
l>m时的非方系统称为瘦系统,当瘦系统满足列满秩时,有
(1)平均频域NRGA的每列元素和的模为1;
(2)平均频域 NRGA第 i行元素之和的模是Ur的第i行2范数的平方,即
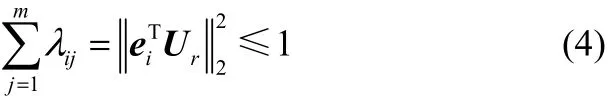
其中,Ur包含了G的前r个输出奇异向量,ei是关于输入 yi的 l×1基向量,ei=[0…010…0]T,其中 1出现在第i个位置。
l<m时的非方系统称为胖系统,当胖系统满足行满秩时,有
(1)平均频域NRGA的每行元素和的模为1;
(2)平均频域 NRGA第 j列元素之和的模是Vr的第j行2范数的平方,即

其中,Vr包含了G的前r个输入奇异向量,ej是关于输入uj的m×1基向量,ej=[0…010…0]T,其中1出现在第j个位置。
根据上列性质,提出了一种控制结构设计方法。
(1)检查系统的能控性。对于一个l×m维多变量系统,当采用完全分散控制时,要保证系统的能控性,必须满足l≤m[26]。但提出的新的复杂控制策略中,由于采用串级控制回路和单回路控制结合的方案,该方案的极限情况是所有回路都采用串级控制回路,因此满足系统能控性的条件是主副被控变量分别独立可控,即满足l≤2m。对于l>2m的系统则无法直接进行复杂控制系统结构设计,需要先根据输出变量对系统的重要性以及是否易于测量,通过控制是否可以“镇定”对象等条件[26]选择 l≤2m个,再进行复杂控制系统结构设计。
(2)利用瘦系统平均频域NRGA的每列元素和的模为1,而每行元素和的模小于等于1的性质,选取平均频域NRGA中行和的模值更接近于1的对应的l-m个输出,组成新系统。由于平均频域NRGA是考虑了系统动态特性的一种变量配对方法,因此行和的模值更接近于1的输出,其响应速度越快,越适合作为串级中的副被控变量。在该新系统中,计算NRGA,选择最接近1的对应输入输出变量组成配对。
(3)对配对完成的回路进行控制器参数设计,将其输出分别看作在步骤(2)中未被选择的输入变量不做转化,重新排列成 ul-m+1,ul-m+2, …, um。对系统传递函数进行相应转换,具体转换方法将在2.3节中说明。
(5)两步分别配对完成后,如果有两个输出变量配对到同一个输入变量上,则对该输入和两个输出变量进行串级控制结构设计。步骤(2)中被选择的灵敏度高的输出变量作为副回路被控变量,步骤(4)中被选择的灵敏度低的输出变量作为主回路被控变量。
2 瘦系统的复杂控制系统结构设计
2.1 串级控制系统
串级控制系统[28-31]由主副两个控制器串联组成,主控制器的输出作为副控制器的给定值,副控制器的输出作为操作变量,来实现对主被控变量的定值控制,其控制原理方框图如图 1所示。其中ym(s)、ys(s)分别为主、副被控变量;Gc1(s)和 Gc2(s)分别为主、副控制器的传递函数;Gv(s)为控制阀的传递函数;Gp1(s)和Gp2(s)分别为主、副对象的传递函数;H1(s)和H2(s)分别为主、副被控变量变送环节传递函数;F1和F2分别为进入主、副被控对象的扰动;Gf1(s)和Gf2(s)分别为主、副回路扰动通道的传递函数。

图1 串级控制系统Fig.1 Cascade control system
串级控制系统有2个被控变量,1个操作变量,属于瘦系统。主被控变量是反映产品质量或生产运行的主要工艺变量,控制系统的目的在于稳定这一变量,使其等于工艺规定的给定值,副被控变量的设置是为提高主被控变量的控制质量服务的,通过引入副回路可以改善主回路的特性,使控制过程加快,迅速克服干扰对主被控变量的影响,实现对干扰的超前控制。常规的非方系统控制结构设计方法往往在方形化时删除其中一个被控变量,没有将所有变量进行反馈,这是不合理的。
2.2 均匀控制
均匀控制是一种为了平衡各变量的稳定性而设计的协调控制方案。在工业流程中,生产设备往往联系紧密,前一工艺对后续生产过程有着很大的影响,而对于输入变量少于输出变量的瘦系统而言,根据传统方化系统的方法,必有若干个被控变量会受其余变量的影响一直波动,无法得到控制和稳定。多变量的串级控制系统则将这些无法得到的控制的被控变量作为串级控制副被控变量,使其快速得到稳定,避免其对其他重要被控变量的影响,达到均衡系统所有被控变量的目的,起到均匀控制的作用。
2.3 瘦系统的复杂控制系统结构设计
对于一般多变量系统,根据工艺过程可以将被控变量划分为重要变量和次要变量。重要变量一般是对生产过程或者产品质量影响较大的变量,如压力、温度等,次要变量指影响相对较小的变量,如流量等。
对于输出变量多于输入变量的瘦系统,如果仅设计都为单回路的简单控制系统,往往很难对所有输出变量进行有效控制,总是有若干个输出变量未纳入反馈,因此系统无法满足控制要求。而串级系统由于存在主、副回路,可以使用一个操作变量和两个被控变量,兼顾重要变量和次要变量的控制要求,因此可以应用到输入变量比输出变量少的瘦系统中。为了方便,以下都省略符号s。
假设系统为 l×m 维,l≤2m。单回路控制记做{yi~uj},串级回路记做{yi1~(yi2~uj)},其中 yi2为副被控变量,yi1为主被控变量,单独出现yi表示该变量没有得到控制。由于系统是l×m维,因此在传统的方化系统方法中必有l-m个输出无法得到控制。
系统的矩阵为
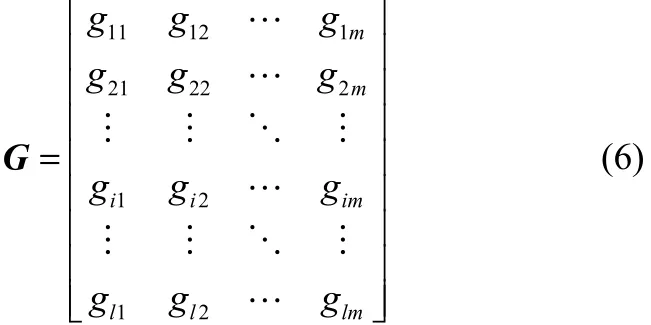
由于第 1步配对中主要挑选响应速度最快的l-m个输出变量,而平均频域NRGA考虑了系统的动态特性,能很好地满足需求,因此该步中使用平均频域NRGA对系统进行关联分析。


对系统G1采用NRGA方法进行输入输出变量配对。将NRGA阵p行元素中最接近1的元素对应的列记作qp,其中p=1, 2, …, l-m,于是得到配对的输入输出对应的传递函数记作gpqp。原系统G的第qp列中未得到配对的其余元素可以表示为giqp,其中i=1,2, …, l-m,i≠p。此时系统G1中的被控变量都为响应较快的被控变量,应作为串级中的副被控变量。
配对完成后,对相应回路进行控制器设置,一般副控制器只含比例环节,假设副回路实现理想控制,对与l-m个输出变量配对成功的输入变量进行重新定义,新定义后的输入变量记作,, …,,其中

设回路中的控制器参数依次为kc1, kc2, …, kc(l-m),则本步配对完成后的闭环回路的等效传递函数为

当一个回路存在多个被控变量,并且副回路已经进行等效计算,输入变量已经进行转化时,主被控对象的传递函数应为副被控变量传递函数和主被控变量传递函数的比值,即


而对于剩余的未进行转化的输入变量 ul-m+1,ul-m+2, …, um,对应传递函数不变,即

即j依次取1, 2, …, m中除去qp的所有列,其中p=1,2, …, l-m;i=1, 2, …, l。
例如,在 4×3系统中,若得到{y1~u1},并且控制器参数为kc1,则传递函数转换为
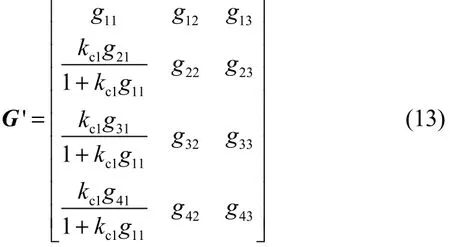
令转化后的输入变量为
信息传播理论认为,沟通过程中沟通主体同时进行着信息的发送和接收,沟通本身是一个循环往复的过程,单方向传播路线会影响交互的效果,反馈在信息传播过程中扮演了非常重要的角色。即时的反馈能够带来更高的受众参与度以及更强的顾客互动性,这使得用户能够更加自如地表达交换自己的感受和见解,也就满足了人们情感宣泄的需要。相比于异步沟通而言,同步沟通模式中,信息沟通是及时的、快节奏的,互动双方能够给予即时的反馈。而在异步沟通模式中,沟通主体的交流频率则较低。[8]可见,同步沟通所带来的即时反馈能够促使个体更加乐意进行自我表露。

对应于新的输入变量u',第1步配对后剩余的输出变量组成新的m×m系统G2

由于此步配对完成后的输出变量是作为串级控制回路中的主被控变量或单回路中的被控变量,因此不需要考虑变量响应快慢问题,为了计算方便,可以利用RGA进行输入输出变量配对。
两步分别配对完成后,对具有相同对应输入变量的两个输出变量进行串级控制结构设计。第1步选择的灵敏度高的输出变量作为副回路被控变量,第2步选择的输出变量作为主回路被控变量。
综上所述,瘦系统串级控制结构的设计方法如下。
(1)检查系统的能控性。
(2)计算系统的平均频域NRGA,选取平均频域NRGA中行和的模最接近于1的对应的l-m个输出,即响应速度最快的变量,与所有输入变量组成新的系统。在该系统中,计算NRGA,选择NRGA中最接近1的元素对应输入输出变量组成配对,此时配对完成的变量将组成串级控制中的副回路。
(3)对配对完成的回路进行控制器参数设计,定义配对成功的输入变量为新的输入变量,, …,,未配对成功的依旧为ul-m+1, ul-m+2, …,。对系统传递函数进行相应转换。
3 实例分析
本节将对两个输出变量维数多于输入变量维数的非方系统使用2.3节中的方法进行控制系统结构设计,例1主要说明该控制系统设计法的均匀控制效果,例2主要说明串级控制效果。
例1:DL精馏塔系统。由Doukas等[30]提出的分离苯、甲苯和二甲苯的混合物的装置如图2所示。表1为DL精馏塔系统各变量的定义,各输入和各输出之间的传递函数。DL精馏塔系统的主要目的为分离苯、甲苯和二甲苯的混合物,主要产品为纯度较高的苯和二甲苯,精馏塔顶部产品为苯,底部产品为二甲苯,侧线的主要产品为甲苯,需要得到控制的是3个产品流中的4个杂质的浓度,y3为侧线中苯的浓度,y4为侧线流中二甲苯的浓度,操纵变量只有3个,分别为再沸器效率,回流比和侧线流量。系统满足能控性条件 l≤2m,其中 l为输出变量个数,m为输出入变量个数,因此可以直接进行复杂控制系统结构设计。

表1 示例系统1的传递函数Table 1 Transfer function of drill 1
计算系统平均频域NRGA阵



图2 DL精馏塔Fig.2 DL distillation column
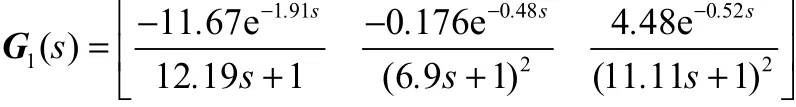
计算系统的NRGA阵

得到合理的配对:{y4~u1}。由于此例中原系统输出个数l=4,输入个数m=3,因此gpqp中p的取值为1,根据NRGA1得到q的取值也为1,于是在新系统G1(s)中的g11,对应于原系统G(s)的g41,即为2.3节中定义的gpqp。对y4回路进行控制器设计,得到kc1=-1,根据2.3节中的式(11)和式(12)得到系统新的传递函数为

下面的步骤确定了应该设计成串级的回路。与式(15)相对应,此例中剩余系统为由被控变量 y1、y2、y3和新的操作变量构成的系统

将数据代入计算得到

计算G2(0)的RGA阵

同理根据RGA配对准则,得到{y1~u3, y2~u2,y3~u1}的配对。因此,y3~(y4~u1)将组成串级控制回路,y4为副被控变量,y3为主被控变量。由以上两步综合得到多变量串级控制系统合理的配对:{y1~u3, y2~u2, y3~(y4~u1)}。而传统的方法是直接利用NRGA对系统进行方化,计算系统NRGA

矩阵行和:0.9985, 1.0000, 0.0301, 0.9715;矩阵列和都为1。得到配对为{y1~u3, y2~u2, y3, y4~u1}。
由于y3和y4的重要程度没有太大区分,因此为了方便比较,令完全简单单回路控制系统为{y1~u3,y2~u2, y3~u1, y4}。
利用MATLAB/Simulink搭建多变量控制系统,控制回路配对为{y1~u3, y2~u2, y3~(y4~u1)},即对y1和y2分别进行单回路控制,而y4作为副被控变量和y3主被控变量构成串级控制。而采用一般方法对系统方化后进行简单单回路控制时的系统为{y1~u3, y2~u2, y3~u1, y4},即对 y1、y2和 y3分别进行单回路控制,而y4未受到控制。当u2单位阶跃变化时,对比两者控制效果,仿真结果如图3所示。图中实线为采用 NRGA对非方多变量系统进行控制配对时,多变量均匀多回路控制系统的仿真结果,虚线为采用系统方化法进行控制变量配对时,多变量完全单回路控制系统的仿真结果。
多变量串级控制系统中非串级回路操作变量设定值的改变给串级回路带来了扰动,由图3可知,系统的响应速度非常快。由于加入了串级控制,多变量串级控制的控制速度远远大于采用方化系统法进行完全单回路控制时的控制速度,y4尤为明显,这从图3(d)中可以看出。由于多变量串级控制系统中y4响应非常迅速,并马上稳定,因此避免了对其他被控变量的影响,使得其余被控变量的控制速度和控制精度也有显著提升,于是串级控制系统中被控变量y1、y2、y3和y4都得到了控制,并且达到了稳定,即各变量得到了均匀控制。而在采用一般方化法进行完全单回路控制时,由于未对y4进行控制,因此该变量在仿真时长内始终处于波动状态。因此,本示例说明使用本控制系统设计方法,能达到均匀控制的目的。

表2 示例系统2的传递函数Table 2 Transfer function of drill 2

图3 u2单位阶跃变化时,输出y分别在串级多回路控制系统中和简单单回路控制系统中的仿真结果Fig.3 y in multi-loop control with cascade control and without cascade control while adding unit step change on u2

图4 Shell系统Fig4 Shell system
例2:Shell系统。Shell系统是由Prett等[31]提出的一套重油分馏塔的线性模型,模拟的过程包括1个反应器段、4个换热器、1个侧面汽提器、1个产品进料和3个产品出料线。图4中描述了该系统的主要工艺过程。表2为Shell系统各变量的定义,各输入和各输出之间的传递函数。系统满足能控性条件l≤2m,其中l为输出变量个数,m为输出入变量个数,因此可以直接进行复杂控制系统结构设计。



计算系统G1(s)的NRGA阵

得到合理的配对:{y3~u1, y4~u2}。由于此例中原系统输出个数 l=5,输入个数 m=3,因此 gpqp中 p应分别取1和2。当p的取1时,根据NRGA1得到q的取值为1;当p的取2时,根据NRGA1得到q的取值为2。于是在新系统G1(s)中的g11和g22,对应于原系统G(s)中的g31和g42,即为2.3节中定义的gpqp。
对 y3和 y4回路分别进行控制器设计,得到kc1=0.24,kc2=0.3,根据 2.3节中的式(11)和式(12)得到系统新的传递函数为

下面的步骤确定了应该设计成串级的回路。
与式(15)相对应,此例中剩余系统为由被控变量y1、y2、y5和新的操作变量构成的系统

计算G2(0)的RGA阵

同理根据RGA配对准则,得到{y1~u1, y2~u2, y5~u3}的配对。因此,y1~(y3~u1)和 y2~(y4~u2)将组成串级控制回路,y3和y4分别为两个串级回路的副被控变量,y1和y2分别为两个串级回路的主被控变量。综上得到配对为{ y1~(y3~u1), y2~(y4~u2),y5~u3}。而传统的方法是直接利用NRGA对系统进行方化,计算系统NRGA
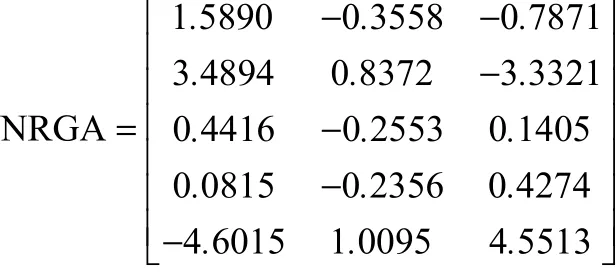
矩阵行和:0.446, 0.995, 0.327, 0.273, 0.959; 矩阵列和:1.000, 1.000, 1.000。因此选取由y1、y2、y5和操作变量构成方形系统G(s)

计算系统G(s)的RGA阵

由此得到配对:{y1~u1, y2~u2, y5~u3}。
图5为示例2的仿真结果。由图5可知,不论是y1、y2还是y5,多变量串级控制系统达到稳定的时间都明显小于一般方化法得到的完全单回路控制系统。也就是说,对于系统中单回路操作变量设定值的改变带来的扰动,多变量串级控制系统的抑制速度远远大于完全单回路控制系统。此外,由于多变量串级控制系统对所有输出变量都进行了反馈,因此控制更为全面和准确,控制效果也有很大的提升。
4 结 论
在过程控制领域,系统的优化得到了很多关注,然而大部分优化都是针对控制变量多于被控变量的胖系统提出的,对于输入变量少于输出变量的瘦系统的优化相对来说进展十分缓慢,目前对于瘦系统的优化控制理论大多依旧基于早前的系统方化法和控制器结构设计法,而针对系统本身的优化关注非常少。
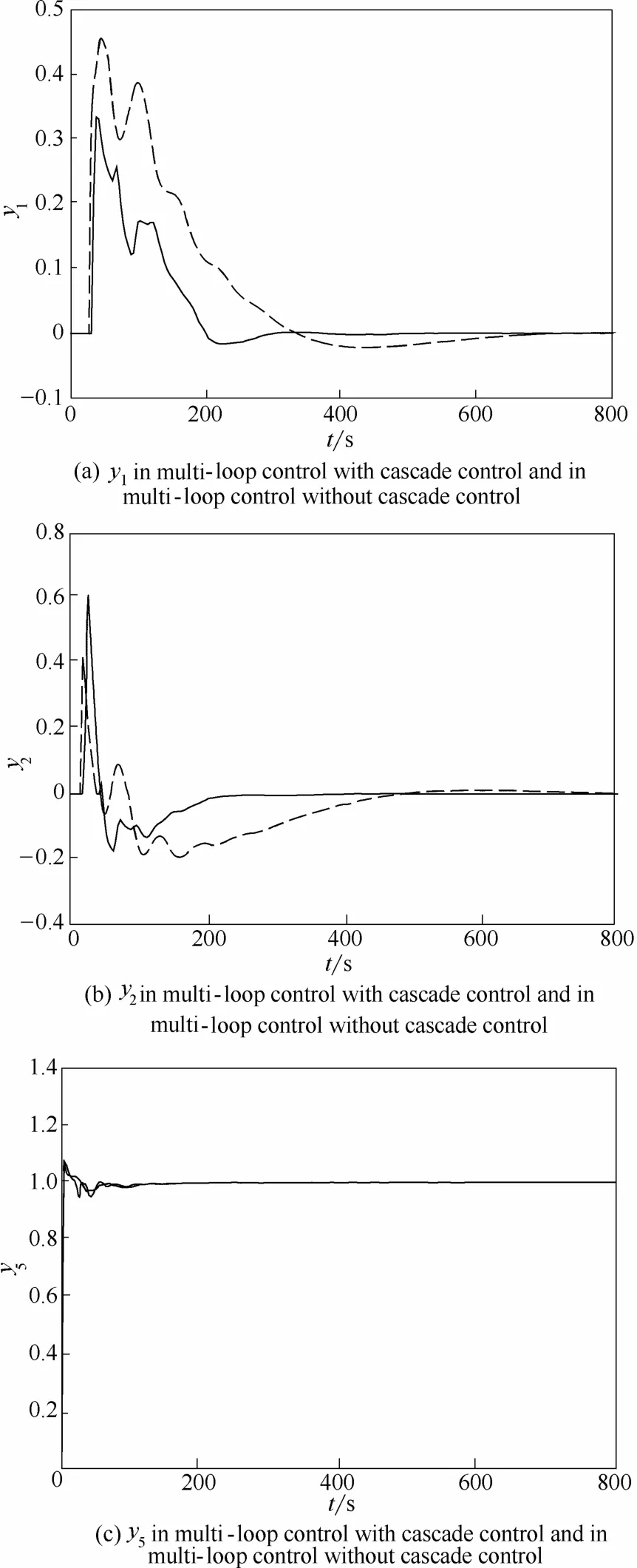
图5 u3单位阶跃变化时,输出y分别在串级多回路控制系统中和简单单回路控制系统中的仿真结果Fig.5 y in multi-loop control with cascade control and without cascade control while adding unit step change on u3
针对输出变量多于输入变量的非方系统本身提出了一种新的控制结构设计方法。对输出变量多于输入变量的瘦系统采用了串级控制回路和单回路控制结合的方法,串级控制系统较单回路系统而言,有效利用了所有的输出反馈信息,使得系统设计更为全面,控制更为准确。这种方法不仅可以用于已知工艺过程的系统,也可以用于只有传递函数已知的系统。研究结果表明,使用这种方法对非方系统进行复杂控制结构设计,不仅能够得到合理的变量配对,而且控制速度显著提升,控制精度也有所提高。
[1] ASTROM K J, JOHANSSON K H, WANG Q G. Design of decoupled PI controllers of two-by-two systems[J]. IEEE Proceedings Control Theory and Application, 2002, 149(1): 74-81.
[2] TAKAGI K, NISHIMURA H. Control of a jib-type crane mounted on a flexible structure[J]. IEEE Transaction on Control System Technology, 2003, 11(1): 32-42.
[3] TAN W, MARQUEZ H J, CHEN T, et al. H1 control design for an industrial boiler[C]// Proceedings of the American Control Conference (ACC), Arlington, USA, 2001.
[4] ASANO K, MORARI M. Interaction measure of tension-thickness control in tandem cold rolling[J]. Control Engineering Practice, 1998,6(8): 1021-1027.
[5] NETT C N. Decentralized control system design for a variable-cycle gas turbine engine[C]// Proceedings of the 28th IEEE Conference on Decision and Control, Tampa, FL, USA, 1989.
[6] SKOGESTAD S, MORARI M. Implication of large RGA elements on control performance[J]. Industrial Engineering Chemistry Research, 1987, 26(11): 2323-2330.
[7] NIEDERLINSKI A. A heuristic approach to the design of linear multivariable control systems[J]. Automatica, 1971, 7(7): 691-701.
[8] BRISTOL E H. On a new measure of interaction for multivariable process control[J]. IEEE Transactions Automatic Control, 1966, 1(1):133-134.
[9] WITCHER M, MCAVOY T J. Interacting control systems: steady state and dynamic measurement of interaction[J]. ISA Transactions,1977, 16(3): 83-90.
[10] MCAVOY T, ARKUN Y, CHEN R, et al. A new approach to defining a dynamic relative gain[J]. Control Engineering Practice, 2003, 11(8):907-914.
[11] GAGNEPAIN J P, SEBORG D E. Analysis of process interactions with application to multiloop control system design[J]. Industrial &Engineering Chemistry Process Design and Development, 1982,21(1): 5-11.
[12] TUNG L S, EDGAR T F. Analysis of control-output interaction in dynamic systems[J]. AIChE Journal, 1981, 27(4): 690-693.
[13] HE M J, CAI W J, NI W, et al. RNGA based control system configuration for multivariable process[J]. Journal of Process Control,2009, 19(7): 1036-1042.
[14] XIONG Q, CAI W J, HE M J. A practical loop pairing criterion formultivariable process[J]. Journal of Process Control, 2005, 15(7):741-747.
[15] 罗雄麟, 任丽红, 周晓龙, 等. 常规控制系统配对设计的动态相对增益阵研究[J]. 化工自动化及仪表, 2012, 39(3): 295-300.LUO X L, REN L H, ZHOU X L, et al. Dynamic RGA for control system configuration of multivariable process[J]. Control and Instruments in Chemical Industry, 2012, 39(3): 295-300.
[16] 任丽红, 刘雨波, 罗雄麟, 等. 多变量时滞系统的关联分析与变量配对[J]. 化工自动化及仪表, 2012, 39(6): 743-746.REN L H, LIU Y B, LUO X L, et al. Association analysis and variable pairing for multivariable system with time delays[J]. Control and Instruments in Chemical Industry, 2012, 39(6): 743-746.
[17] CHEN D, SEBORG D E. Relative gain array analysis for uncertain process models[J]. AIChE Journal, 2002, 48(2): 302-310.
[18] KARIWALA V, SKOGESTAD S, FORBES J F. Relative gain array for normbounded uncertain systems[J]. Industrial and Engineering Chemistry Research, 2006, 45(5): 1751-1757.
[19] KHAKI-SEDIGH A, MOAVENI B. Relative gain array analysis of uncertain multivariable plants[C]// Proceedings of the 7th European Control Conference, Cambridge, UK, 2003.
[20] KHAKI-SEDIGH A, MOAVENI B. Adaptive input-output pairing using online RGA identification[C]// Proceedings of the 1st African Control Conference, Cape Town, South Africa, 2003.
[21] MOAVENI B, KHAKI-SEDIGH A. On-line input-output pairing for linear and nonlinear multivariable plants using neural network[C]//Proceedings of the International Control Conference, Glasgow,Scotland, 2006.
[22] MOAVENI B, KHAKI-SEDIGH A. Further theoretical results on relative gain array for norm bounded uncertain systems[J]. Industrial and Engineering Chemistry Research, 2007, 46(24): 8288-8289.
[23] YU C C, LUYBEN W L. Robustness with respect to integral controllability[J]. Industrial and Engineering Chemistry Research,1987, 26(5): 1043-1045.
[24] 许锋, 潘琦, 王一岚, 等. 工业过程多变量系统常规控制结构设计的频域方法[J]. 清华大学学报, 2016, 5(4): 448-452.XU F, PAN Q, WANG Y L, et al. Frequency domain design method for decentralized control of multivariable processes[J]. Journal of Tsinghua University (Sci. & Technol.), 2016, 5(4): 448-452.
[25] CHANG J W, YU C C. The relative gain for non-square multivariable systems[J]. Chemical Engineering Science, 1990, 45(5): 1309-1323.
[26] SKOGESTAD S, POSTLETHWAITE I. Multivariable Feedback Control: Analysis and Design[M]. New York: John Wiley & Sons,1996.
[27] 任丽红, 罗雄麟, 刘雨波, 等. 一种新的变量配对方法及其在非方系统中的应用[C]//第十届智能控制与自动化世界大会, 中国北京,2012.REN L H, LUO X L, LIU Y B, et al. A new variable pairing method and its application in non-square multivariable systems[C]//Proceedings of the 10th World Congress on Intelligent Control and Automation, Beijing, China, 2012.
[28] 蒋慰孙, 俞金寿. 过程控制工程[M]. 北京: 中国石化出版社, 1999.JIANG W S, YU J S. Process Control Engineering[M]. Beijing: China Petrochemical Press, 1999.
[29] 王树青, 戴连奎, 于玲. 过程控制工程[M]. 北京: 化学工业出版社, 2008.WANG S Q, DAI L K, YU L. Process Control Engineering[M].Beijing: Chemical Industry Press, 2008.
[30] DOUKAS N, LUYBEN W L. Control of sidestream columns separating ternary mixtures[J]. Automation in Petro-Chemical Industry, 1979, 61(4): 1124-1133.
[31] PRETT D M, MORARI M. Shell Process Control Workshop[M].Stoneham: Butterworth Publishers, 1987.
Cascade control configuration design for non-square multivariable system of chemical processes
XU Feng, YUAN Weiwei, LUO Xionglin
(Department of Automation, China University of Petroleum, Beijing 102249, China)
Chemical processes are usually multivariable systems, which non-square system with more outputs than inputs is known as thin system. Till now, the most common method of designing control configuration for thin systems is to form square systems by increasing or decreasing variables such that only fully decentralized PID control could be achieved with one input pairing to one output. Some critical process variables cannot be used as controlled variables or non-critical variables cannot be included in feedback loops, so the control system often does not meet requirements. With introduction of a non-square gain array relative to average frequency, a method for designing cascade control configuration was proposed through analyzing variable pairing in thin systems. This method fully utilized feedbacks of all output variables without addition of new input variables, so system feedback was more complete and a cascade control was developed for both critical and non-critical variables. Two case study showed that this method achieved not only proper variable pairing but also good control performance especially in speed and efficiency of interference reduction.
process control; process systems; multivariable system; thin system; interaction analysis; variable pairing; cascade control system
date:2016-10-27.
XU Feng, xufeng@cup.edu.cn
supported by the Science Foundation of China University of Petroleum, Beijing (2462015YQ0510) and the National Natural Science Foundation of China (21676295).
TQ 021, TP 273
A
0438—1157(2017)07—2833—11
10.11949/j.issn.0438-1157.20161515
2016-10-27收到初稿,2017-04-10收到修改稿。
联系人及第一作者:许锋(1976—),男,博士,副教授。
中国石油大学(北京)科研基金项目(2462015YQ0510);国家自然科学基金项目(21676295)。

