连续刚构桥组合式桥墩合理分界点研究

王 俏，李 彪，杨美良

(1. 长沙理工大学 土木与建筑学院，湖南 长沙 410004; 2.湖南省永吉高速公路建设开发有限公司，湖南 吉首 416000)

连续刚构桥组合式桥墩合理分界点研究

王 俏1，李 彪2，杨美良1

(1. 长沙理工大学 土木与建筑学院，湖南 长沙 410004; 2.湖南省永吉高速公路建设开发有限公司，湖南 吉首 416000)

以高墩稳定性能分析为目标，基于结构弹性屈曲稳定理论中的常用方法能量法，推导了组合式桥墩面外与面内稳定系数的计算公式；以默戎高架桥为依托工程，在稳定性理论基础上分析该桥的分界点位置，分别求得其面内稳定系数和面外稳定系数并使其相等，即可得到119.2 m的8#墩合理分界点位置为L1=72.712 m，L2=46.488 m,此时L1=0.61L,并求得此时面外面内稳定系数均为22.13。

连续刚构桥； 组合式桥墩； 面外稳定系数； 面内稳定系数； 合理分界点

0 引言

桥墩是桥梁上部结构及下部基础的中间部位，对桥梁结构整体受力与变形起着承上启下的关键作用。通常高度在40 m 以下的桥墩只需考虑截面的强度，对于高度超过40 m的高桥桥墩，桥墩的面内面外稳定性能则是桥梁设计的控制性因素[1]。

连续刚构桥常见的桥墩形式有：独墩、双薄壁墩和上部为双薄壁墩下部是独墩的组合型式桥墩[2]。独墩的抗推刚度大，在相同的墩高条件下，由上部结构传递的弯矩大；双薄壁墩抗推刚度低，由上部结构传递的弯矩小。现今由于实际施工条件的限制，在工程中仍较常采用的桥墩形式为双薄壁墩和独墩两种；但是由于组合型式桥墩结构相应具备双薄壁墩与独墩两者的结构优势，并可以通过改变设计来变化上部双薄壁墩与下部独墩的分界位置，使之得到合理的横向刚度与纵向刚度[3]，并满足桥墩在施工阶段与成桥运营后稳定性要求，所以近年来组合型式桥墩越来越成为山区高墩连续刚构桥的优先选择。一些学者对组合型式桥墩作了研究：李安渠[4]通过有限元分析了组合型式桥墩在最大悬臂状态的墩身的屈曲理论，在此基础上得出分界点位置为0.5时稳定性较好的结论；李璐[5]对组合型式桥墩不同分界点比例在各阶段时做了非线性屈曲分析，提出分界点比例合理范围为0.5～0.67；周水兴[6]根据能量法理论中的瑞丽-里兹法，得出了组合型式桥墩在最大悬臂施工阶段时面外屈曲系数公式，给出了组合型式桥墩合理分界点比例的建议值；王磊、李家宝[7]提出关于高层框架结构的相关结论，表明柱的轴向形变对主梁转角位移方程存在较大影响。

本文基于组合型式桥墩面内外稳定分析，对组合型式桥墩的双薄壁墩和独墩的分界点合理位置进行深入研究和讨论。运用能量法，在一端固定、一端自由的单悬臂支柱欧拉临界点微分方程的理论上，得到求解面内外稳定系数公式，根据合理分界点的比例即为组合型式桥墩面内外稳定性能相同时这一基本原理，就得到工程实例的分界点理论值并得出此时的内外稳定系数。

1 组合型式桥墩稳定性分析理论

能量法是分析高桥稳定性能的一种常用方法，其中心思想是在势能驻值原理基础上将结构失稳时的位移曲线用一个具有广义坐标的位移函数来近似替代，将原本需要求解无限个变量的泛函情况转化为只需要求解有限个变量的函数极值问题。然后对总势能函数求导数，便求得一个代数方程组，再根据条件求解此代数方程组即得到结构的屈曲临界系数。

1.1 面外弹性稳定屈曲系数计算公式

组合型式桥墩的面外屈曲分析计算简图可由图1所示。假设为一端固定、一端自由的单悬臂支柱建立欧拉临界力微分方程,分析其面外稳定性能，本文选取的位移函数为两项三角函数之和，且位移函数满足便于积分、满足边界条件和力学边界的条件。

图1 组合型式桥墩面外稳定屈曲分析简图

1)选取组合型式桥墩处于面外失稳临界状态时的位移函数为：

(1)

2)基于结构处于屈曲临界状态时结构变形势能的变化值与外力势能的变化值相等这一理论基础，可以建立相应结构体系的能量平衡方程。

临界失稳阶段时结构的弯曲应变能为：

(2)

(3)

临界失稳阶段时结构的外力势能为：

(4)

而结构体系总势能：

Π=U+V

(5)

分别对a1、a2求偏导，就把转化为求结构总势能Π的极值问题，得：

(6)

带入相关数据计算得：

(7)

(8)

式中：

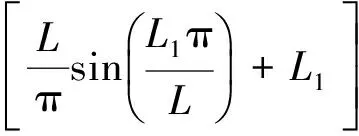
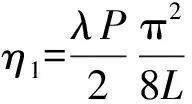
把总势能Π分别用参数a1、a2表示可得到：

(9)

(10)

(11)

当方程组有非零解时，满足其系数矩阵的行列式的值为零，即：

(12)

由式(12)展开便可以得到一个一元二次方程，此方程即为结构体系稳定方程，求解该方程并取它满足条件时的较小的解即为结构体系的面外屈曲系数：

(13)

式(13)中ξ1、ξ2、ξ3同前所述。

1.2 面内弹性屈曲系数公式

组合型式桥墩的面内屈曲分析简图为图2所示。可将主梁、双薄壁墩及独墩结构等效为单跨双层框架结构进行面内稳定分析，高层结构在无防侧移支撑下会首先出现反对称屈曲[8]。

图2 组合型式桥墩面内稳定屈曲分析简图

1) 考虑轴向变形影响的主梁转角位移方程：

(14)

(15)

2) 选取失稳后位移函数为2个三次多项式，根据相关边界条件将多项式系数分别用uA、uB表示：

下部独墩失稳后阶段的变形函数及其求导数有：

(16)

上部双薄壁墩失稳后变形函数及其一阶、二阶导数：

(17)

根据边界条件计算多项式系数：

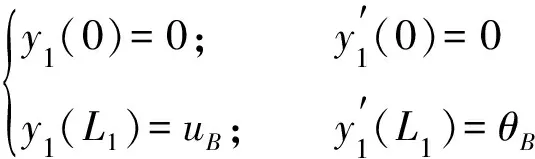
(18)

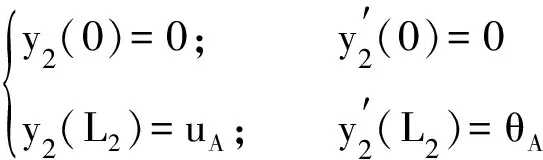
(19)

3) 建立双薄壁墩与独墩交界点位置的弯矩平衡方程，此时双薄壁墩的弯矩加上柱子轴力与双肢距离的乘积等于下部独墩的弯矩，根据这一关系，将交界点位移用uA、θA表示：

MB C=2MBA-NA Blb

(20)

又因为：

(21)

得到:

EI1(6AL1+2B)=4EI2b-ηABθAlb

(22)

带入相关数据计算得：

(23)

(24)

4) 得到结构处于稳定临界状态时体系总势能。

① 结构变形势能为：

下部独墩弯曲应变能：

(25)

双薄壁墩弯曲应变能：

(26)

② 外力势能为：

下部独墩外力势能为：

(27)

上部双薄壁墩外力势能为：

(28)

结构体系的总势能为：

Π=U1+U2-V1-V2

(29)

(30)

由式(30)可得一个方程组：

(31)

若要使方程组有非零解，则方程组系数矩阵的行列式为零：

(32)

由式(32)可以得到一个关于屈曲系数的一元二次方程，此方程即为要求的结构稳定方程，求解该稳定方程得到方程的解为式(33)，并取得它的最小解就可得到结构的最小屈曲临界系数。

(33)

式中：

2 组合型式桥墩合理分界点位置

2.1 工程背景

本文依托默戎高架桥实际工程背景分析其面外面内稳定性。默戎高架桥为95 m+3×170 m+95m的预应力混凝土连续刚构桥；主梁的截面形式为单箱单室，主梁为跨中高3.75 m，根部10.75 m,梁高沿跨中到根部按1.8次抛物线变化；箱梁的顶板厚度为0.28 m；底板厚度从跨中的0.32 m 按1.8次抛物线渐变至根部的1 m；腹板厚度从跨中到根部依次为0.5、0.6、0.7、0.9 m，零号块腹板厚度为0.9 m。大桥的主墩号分别为7#、8#、9#、10#，全桥最高墩为8#，结构形式为上部双薄壁墩、下部为三室的独墩的组合型式桥墩，桥墩高度为129.2 m；薄壁墩横桥向宽度为8.0 m、壁厚0.7 m，纵桥向宽度为3.0 m、壁厚0.7 m，墩顶设置5.0 m的实心段；下部独墩采用的是三室的截面形式，横桥向宽度为8.0 m、壁厚0.7 m，纵桥向长度为14 m、壁厚0.7 m。默戎高架桥桥型布置形式如图3，8#桥墩上部双薄壁墩和下部独墩截面尺寸如图4所示。

2.2 8#墩面内外屈曲计算

1) 8#墩面外屈曲计算。

根据实例数据有：E=3.45×1010，E为弹性模量；Ib=469.3 m4,I1=904.348,I2=15.747；AAB=13.44 m2，表示上部双肢薄壁墩横截面积；lb=11 m,L1=69.2 m,L2=50 m；P=75 513 793N。

带入相关数据得：

2) 8#墩面内屈曲计算。

将各表达式计算值代入计算得：

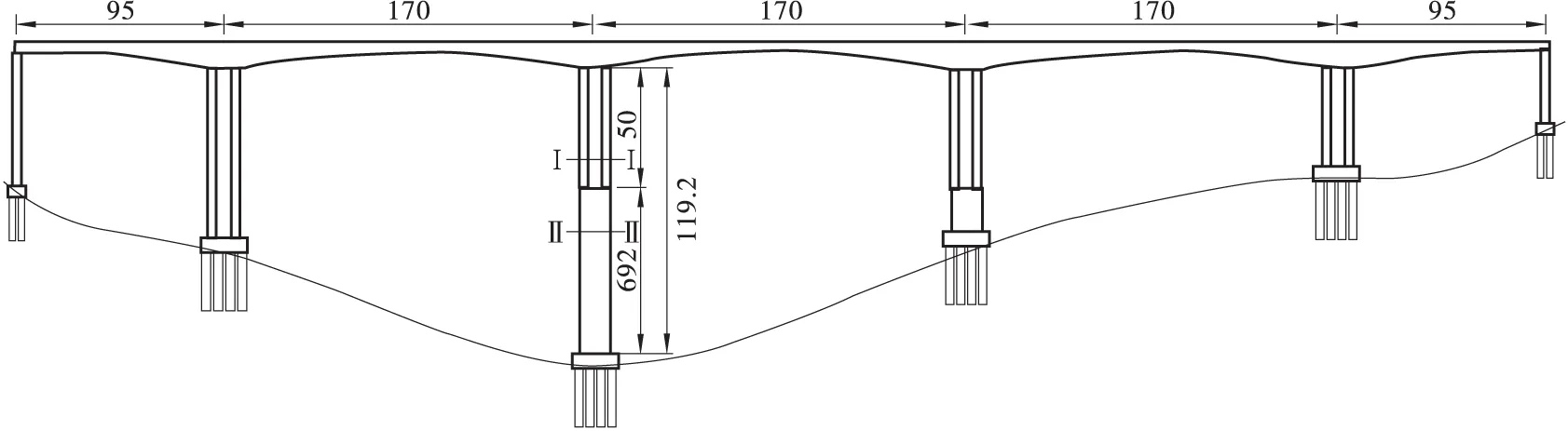
图3 默戎高架桥立面桥型布置图 (单位： m)

图4 默戎高架桥8#桥墩截面尺寸(单位： m)

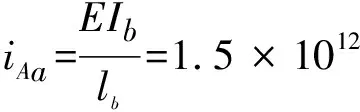
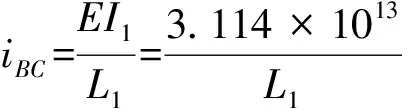
式中:i表示各部分的线刚度。

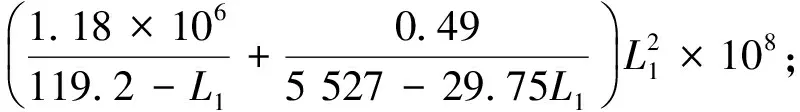
根据求得的数据代入可得：

代入各参数得：

2.3 合理分界点位置

一般来说，当组合型式桥墩的面内面外稳定性能相同，此时的分界点就是桥墩的合理分界点。以默戎高架桥为背景，求得其面内稳定系数和面外稳定系数使其相等，即可得到合理分界点位置。

根据式(13)、式(33)令：

面内面外稳定性能相同时即λ=q，得到关于L1的一元二次方程，求解方程可以得到满足稳定系数要求的正值解为L1=72.712 m，L2=46.488 m,此即为结构合理分界点位置，此时L1=0.61L。将L1、L2、L值分别代入面外面内稳定性系数公式(13)和式(33)，得到此时的面内面外系数相等为22.13。

组合型式桥墩下部独墩与上部双薄壁墩的高度比例是很重要的设计参数，确定合理的分界点位置使得组合式桥墩的结构合理、满足受力要求对组合式桥墩的设计至关重要，因此通过公式推导方式可以很好地推进对于组合式桥墩合理分界点的研究。

3 结论

1)本文基于能量法的稳定理论，在一端固定、一端自由的单悬臂支柱欧拉屈曲失稳临界力微分方程的基础上,分别得到组合型式桥墩的面内外稳定系数公式，面内面外稳定系数均可通过求解一元二次方程求得相应的解。

2)依托默戎高架桥实际工程背景，分别求得将推导的面内面外稳定系数计算公式的结果，令面内面外稳定系数相等时，求得组合型式桥墩的合理分界点位置为L1=72.712 m，L2=46.488 m,此时L1=0.61L,并求得此时面外面内稳定系数均为22.13。

3)高层结构在无防侧移支撑下会首先出现反对称屈曲，但是本文组合式桥墩面内弹性屈曲系数求解时，没有考虑柱子的轴向变形对主梁转角位移方程的影响，对结果的精确性有一定的影响，求解得到的最优解可能不是整体最优解，因此下一步的研究将从考虑轴向变形类型的方案展开讨论。

[1] 马保林.高墩大跨连续刚构桥[M]. 北京：人民交通出版社, 2001.

[2] 叶文军. 大跨度连续刚构桥超高墩合理构造形式研究[D].重庆：重庆交通大学,2015.

[3] 李璐. 超局墩连续刚构桥桥墩构造及稳定研究[D]. 重庆：重庆交通大学，2012.

[4] 李安渠. 大跨预应力连续刚构桥高墩优化设计研究[J]. 公路， 2011(6) .

[5] 李璐,周水兴,江雄飞. 双薄壁-独墩组合型桥墩合理构造形式研究[J]. 重庆交通大学学报(自然科学版)，2012(1) .

[6] 周水兴,满泽联,周光强,等.连续刚构桥组合式桥墩临界荷载分析[J]. 重庆交通大学学报(自然科学版)， 2014(1) .

[7] 王磊,李家宝.高层结构精确计算法[M].上海：上海科学技术出版社, 1989.

[8] 韦成龙,相其生,曾庆元.双薄壁高墩连续刚构桥稳定性分析的Ritz法[J]. 长沙交通学院学报, 2006(3) .

1008-844X(2017)02-0130-05

U 448.23

A