考虑桩间土非线性影响的刚性桩复合地基桩土应力比计算方法研究

朱桃丽,赵桂娥

(1.湖南省建筑科学研究院，湖南 长沙 410000；2.湖南省交通科学研究院，湖南 长沙 410015)

考虑桩间土非线性影响的刚性桩复合地基桩土应力比计算方法研究

朱桃丽1,赵桂娥2

(1.湖南省建筑科学研究院，湖南 长沙 410000；2.湖南省交通科学研究院，湖南 长沙 410015)

考虑桩侧摩阻力与桩 — 土相对位移的双曲线关系以及桩间土体非线性变形影响的特点，建立刚性桩复合地基土体压缩模量与应变的关系模型。考虑桩土竖向变形，采取桩体向上刺入褥垫层及向下刺入持力层的模型，引进分级加载的思想，基于桩-土-垫层的竖向变形协调条件，最后得到了刚性桩桩土应力比。通过对某工程进行现场实测试验数据对比，分析得到了桩侧摩阻力与桩身正应力的分布规律，同时对垫层厚度、垫层模量、桩长、桩土加固区土体模量等参数进行了分析，结果表明该方法具有一定的合理性和可行性。

刚性桩复合地基； 竖向变形；分级加载；桩土应力比；非线性

0 引言

刚性桩复合地基由于其承载力高、沉降小、造价适中等优点，而被广泛应用于高速公路路基处理工程[1，2]。与此同时，其设计计算理论也越来越受到学术界的广泛关注。桩土应力比是反映刚性桩(如素混凝土桩、CFG桩等)复合地基工作状态的重要参数，是承载力设计、变形控制和沉降计算的重要指标。在刚性桩复合地基中，褥垫层的设置能有效地调整桩土的受力情况，减轻桩顶应力集中现象，充分利用桩间土的承载力[3]。然而由于褥垫层的设置，刚性桩会有向上刺入褥垫层的变形，同时，刚性桩也会刺入持力层，使得这种复合地基的受力更复杂。目前常用的规范法[4]不能考虑桩土相互作用，须事先估计桩土应力比，由于刚性桩复合地基桩土应力比取值跨度范围过大，难以准确选取，这为刚性桩设计计算带来了一定困难。

对于上述问题，近年来不断有学者提出相关的桩土应力比计算方法。傅景辉等[5]结合桩身上下刺入模型，分别考虑“桩顶-垫层”、“桩端-下卧层”的应力相等与变形协调，提出了刚性桩复合地基的桩土应力计算方法，建立了目前最为常用的考虑“垫层-桩土加固区-下卧层”共同作用的一维压缩模型，但该方法未考虑桩土相互作用。朱世哲等[6]假定全桩正摩阻力并呈线性分布，在文献[5]研究思路的基础上，提出了刚性桩桩土应力比计算公式，而这一假设未考虑桩身负摩阻力区，与刚性桩实际受力状态不符。郭忠贤等[7]沿桩身进行了正负摩阻力分区，同样假定摩阻力呈线性分布，提出了考虑桩土相互作用的桩土应力比计算方法。赵明华等[8]、缪林昌等[9]同样进行了摩阻力分区，并将其分布模式假定为更为简单的均匀分布。高琼等[10]考虑桩土相互作用，引入剪切位移的思想，提出了柔性基础下刚性桩复合地基桩土应力比与沉降计算方法。而对于刚性桩来说，由于桩土刚度差异较大，桩土界面必然产生相对滑移，且大量试验证明桩侧摩阻力分布并非简单的呈线性分布。张军等[11]引入理想弹塑性模型描述摩阻力与桩土相对位移的关系。赵明华等[12]与李鹏云等[13]则分别考虑摩阻力与桩土相对位移呈双曲线关系，对刚性桩荷载传递进行了分析。综上所述，目前刚性桩复合地基分析方法基本是在一维线性压缩模型的基础上，围绕“垫层-桩-土-下卧层”相互作用进行展开，然而桩间土多为软弱土，在受力变形过程会呈现一定非线性特性，上述模型均未考虑这一因素。

为此，本文在一维压缩模型的基础上，考虑桩间软土非线性变形特性对桩土相互作用的影响，引进分级加载的思想，考虑桩土加固区与垫层以及下卧层的变形协调，得出了桩土应力比计算的新方法，并利用某实际工程对本文方法进行了验证，在此基础上进行了相关参数分析，旨在为刚性桩复合地基受力分析提供一种新的思路。

1 计算模型的建立与分析

1.1 模型示意图

根据工程实践，本文分析时，取复合地基中单桩及其处理范围内的地基土为研究对象，建立分析单元体，单元体如图1所示。桩长为Lp，直径为dp，单桩加固范围直径de，de可以由桩的间距和布桩方式按de=cgsd确定，sd为桩间距，采用三角形布桩时cg取1.05，正方形布桩时cg取1.13。

图1 分析单元体

将桩身划分为N段，各段结点编号自上而下为i=1，2，.…，N+1，桩身单元厚度均为lp；与桩身部分结点位置对应，土体从上至下也划分为N层，每层土厚度为ls,i0，Es,i0为第i层土体初始压缩模量。刚性桩复合地基受力变形示意图如图2所示。

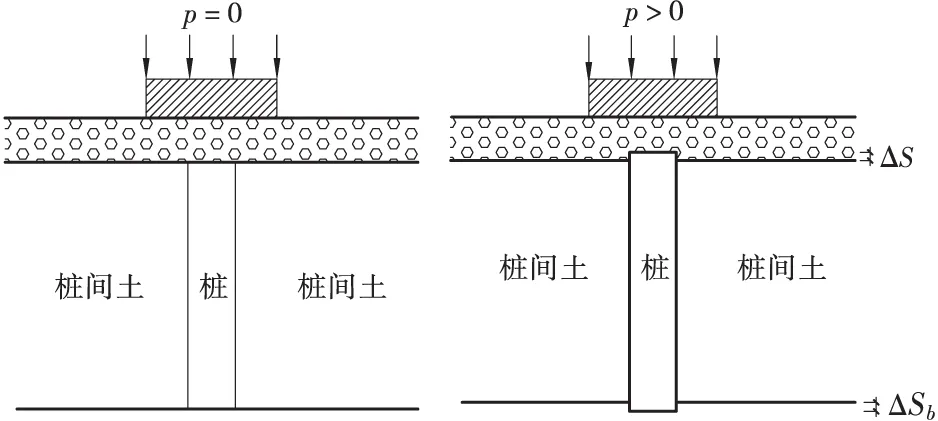
图2 刚性桩复合地基变形示意图

由于本文考虑了桩间土非线性变形特性，难以直接求解桩土变形，故引入分级加载思想，将上部荷载分为M级，在第j级荷载pj作用下，假设均布荷载经过褥垫层的调整之后作用于桩顶荷载为pp,j，作用于桩间土体顶面荷载为ps,j，两者满足如下关系：

mpp, j+(1-m)ps ,j=pj

(1)

式中，pj为作用于垫层顶部的第j级荷载，m为置换率。

1.2 桩顶向垫层刺入量计算

在j级荷载作用下，桩顶刺入量可以由下式得到：

(2)

式中，Δsj为j级荷载下桩顶刺入量；Cu为垫层单位压力刺入量。

Cu可由下式确定：

(3)

式中，Lm为垫层的厚度；Em为垫层压缩模量。

1.3 桩间土及桩身压缩量计算

第i层桩单元和土单元受力如图3所示，根据桩、土单元竖向力的平衡条件，桩间土单元压缩量δs,ij和桩身单元压缩量δp,ij分别通过下式求得：

(4)

式中：σp,ij、σs,ij分别为第j级荷载作用下第i层桩体、土体单元上表面竖向应力；Δεp,ij与Δεs,ij分别为j级荷载作用下桩与桩间土产生的压应变；Es,i(j-1)为j-1级荷载作用下第i层土体压缩模量；ls,i(j-1)为j-1级荷载作用下第i层土体厚度；Ep为桩的弹性模量。

第j级荷载作用前后桩间土体的模量会随着荷载的作用发生变化，这便是土体变形的非线性表现，本文将荷载作用下的土体抽象为由土骨架和孔隙两部分组成，认为土体的总荷载由土骨架承担，孔隙部分不承受荷载，土体的压缩模量为Es，骨架压缩模量为Esf，孔隙率为ρv，文献[14]认为Esf在荷载作用下保持不变且Es与Esf可用下式近似表示：

Es=(1-ρv)Esf

(5)

(6)

式中：Ap为桩身横截面积。

在第j级荷载作用下第i层桩间土体发生压缩变形增量Δzs,ij，此时圆柱单元体的体积为：

(7)

一般认为土体骨架在受荷载前后体积不可压缩，则有：

(8)

式中：ρv,i(j-1)、ρv,ij分别为第j-1级和第j级荷载作用下第i层土体孔隙率。

将式(6)、式(7)代入式(8)，整理可得：

(9)

对式(9)进一步化简，可得：

(10)

结合式(5)，可得桩间土体在第j级荷载作用前后模量的递推关系为：

(11)

式中：Es,ij、Es,i(j-1)分别为第j级和第j-1级荷载作用后刚性桩复合地基第i层土体压缩模量。

1.4 桩土竖向应力递推关系

结合式(4)，前j级荷载下，第i层土单元的厚度为：

(12)

式中：δs,ik为在第1级荷载至第j级荷载之间的某一个k级荷载作用下，第i层桩间土单元压缩量。

在j级荷载作用下，第i层桩、土上表面相对位移为：

(13)

式中：δs,kl为在第1级荷载至第j级荷载之间的某一个l级荷载作用下，第1层至第i-1层之间的某一个k层桩间土单元压缩量；δp,kl为在第1级荷载至第j级荷载之间的某一个l级荷载作用下，第1层至第i-1层之间的某一个k层桩身单元压缩量。

参照前人研究成果[15]，桩土界面摩阻力与相对位移符合Castelli双曲线模型，在第j级荷载下，第i层桩、土界面摩阻力增量为：

(14)

式中：Ki(j-1)为第i层桩侧土在第j-1级荷载作用下的初始切线刚度；τu,ij为第j级荷载下第i层桩侧土的极限摩阻力。

根据Berrum公式，桩土界面初始刚度与极限摩阻力分别为：

(15)

式中：rm为有效影响半径，一般按rm=2.5ρLp×(1-vs)求出，vs为土的泊松比；rp为桩的半径；Gs,i(j-1)为第i层桩侧土在第j-1级荷载作用下的剪切模量，可通过压缩模量计算；K0,i为第i层土的静止土压力系数；φs,i为第i层桩土间摩擦角；γs,k为第1层至第i-1层之间某一个k层桩侧土的重度；ls,k0为第1层至第i-1层之间某一个k层土厚度。

如图3所示，所以在求出第j级荷载作用下第i层桩土摩阻力Δτps,ij之后，分别根据桩、土竖向静力平衡公式，可以求得第i层土单元和桩单元的

图3 桩单元和土单元受力图

下表面应力为σs,(i+1)j、σp,(i+1)j：

(16)

1.5 桩底向下卧层刺入量计算

在求得桩端应力ppb,j和下卧层顶面桩间土附加应力psb,j之后，也即第N层桩土底面的应力σp,(N+1)j、σs,(N+1)j，可求得桩端刺入量：

(17)

式中：Cb为下卧层单位压力刺入量，可由公式(18)确定。

(18)

式中：Eb为下卧土层压缩模量；vb为下卧土层泊松比；ω为沉降影响系数。

1.6 桩土应力比计算

结合上述分析，以桩顶刺入量Δs为试算变量，以下卧层刺入量Δsb为判别条件，本文采用Matlab编制了相应的计算程序，计算过程如下：

1) 假定第j级荷载pj作用下桩顶差异沉降Δsj，即Δps,1j，根据式(1)、式(2)，得到桩顶应力pp,j以及桩间土表面应力ps,j。

2) 根据式(4)获得第1层桩土单元在j级荷载下的压缩量δp,1j与δs,1j，同时根据式(13)～式(15)可以得出桩侧摩阻力增量Δτps,1j。

3) 根据式(16)获得第2层桩土单元竖向应力σs,2j、σp,2j，将其代入式(4)，获得第2层桩土单元在j级荷载下的压缩量δp,2j与δs,2j，而后通过式(13)获得Δps,2j，同时根据式(14)～式(16)可以得出第3层桩土单元底面的应力σp,3j、σs,3j。

4) 重复循环步骤3)直到底层桩土体，得到σp,(N+1)j、σs,(N+1)j与Δps,(N+1)j，即ppb,j、psb,j与Δsb1,j。

5) 在确定第N层桩土体底面应力ppb,j和psb,j后，通过式(17)、式(18)获得桩端刺入持力层深度Δsb2,j。

按照上述过程逐次计算每一级荷载，直到第M级荷载，利用式(1)、式(2)得到最终桩土应力比n。

2 算例验证

湖南某公路工程高填方段须穿越一深厚软土区域，各土层物理力学参数如表1所示，为保证地基满足设计要求，采用长螺旋灌注桩进行加固处理，设计桩径0.6 m，正方形布桩，桩间距1.8 m，施工完成后铺设30 cm厚碎石垫层，垫层压缩模量取30 MPa，铺设完成后取路堤中心下一工程桩，进行复合地基载荷试验。

表1 试验点地基土物理力学参数

将测试结果与本文理论方法求得的桩土应力比进行比较，得出的结果如图4所示。

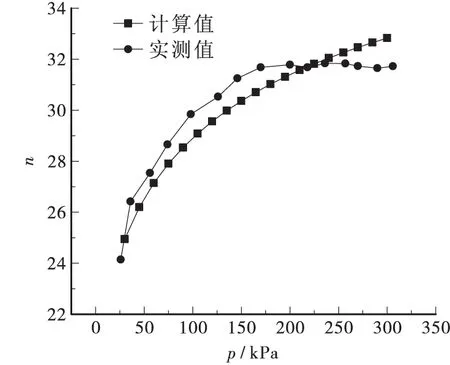
图4 试验点桩土应力比对比图

从对比中可以看出，计算结果与实测结果总体来说较为接近。桩土应力比随荷载的增加而增大，这是由桩土相互作用导致桩土之间的荷载转移决定的，但趋势逐渐减小，这主要由两方面原因造成，一方面是由于桩间土自身的非线性，其在压实过程中的刚度不断增大，导致了桩土刚度比不断减小；另一方面则是由于桩土界面摩阻力与相对位移的非线性，导致桩与土的荷载转移效率不断降低，如图5与图6所示。

图5 桩侧摩阻力分布规律

图6 桩身正应力分布规律

图6所示本文得到的桩身应力变化曲线与文献[16]采用数值模拟方法所得的结果一致，此外，从图5可以看出，当荷载很大时，桩侧摩阻力近似呈线性分布，而荷载小于165 kPa时，桩侧摩阻力沿桩身呈非线性分布，而在公路工程中多数中低路堤荷载并不能达到这一量级，因此目前常用的基于摩阻力线性分布模式的计算方法不适用于中低路堤的情况。

3 参数分析

在算例参数的基础上，根据本文方法，对桩土应力比的各影响因素的敏感性进行对比分析。

3.1 桩土应力比与垫层模量的关系

在其他参数不变的情况下，改变垫层模量Em的大小，由此获得其对桩土应力比的影响如图7所示。由图7可知：在同一级荷载下，桩土应力比随着垫层模量的增大而逐渐增大，但是随着垫层模量的增大，桩土应力比增大的幅度减小。在垫层模量不变的情况下，桩土应力比随着荷载的增大而逐渐增大，最后趋于稳定。但在垫层模量较小时，增大的幅度比垫层模量较大时更小。然而在实际工程中桩土应力比既不能太大也不能过小，因此，选择合理的垫层材料也可以充分发挥桩间土的承载作用。

图7 桩土应力比随垫层模量的变化关系

3.2 桩土应力比与桩长的关系

在其他参数不变的情况下，改变桩长Lp的大小，由此获得其对桩土应力比的影响如图8所示。根据图8可知：在同一级荷载下，桩土应力比随着桩长的增大而逐渐增大，增大的幅度呈现减小的趋势，在荷载较大时，这种增大的效果更加明显。在保持桩长不变的情况下，桩土应力比随着荷载的增大而逐渐增大，最后达到稳定。当桩长达到某一值时，对桩土应力比的影响不再明显，说明复合地基中临界桩长的存在，当桩长小于该值时，增加桩长对提高桩土应力比是有利的。

图8 桩土应力比随桩长的变化关系

3.3 桩土应力比与垫层厚度的关系

在其他参数不变的情况下，改变垫层厚度Lm的大小，由此获得其对桩土应力比的影响如图9所示。根据图9可知：在同一级荷载下，桩土应力比随着垫层厚度的增大而逐渐减小，其减小的幅度呈递减的趋势。在保持垫层厚度不变的情况下，随着荷载的增大，桩土应力比逐渐增大，最后趋于稳定。因此说明并非垫层厚度越大越好，选择合理的垫层厚度也可以充分发挥桩间土的承载作用。

图9 桩土应力比随垫层厚度的变化关系

3.4 桩间土初始模量的影响

在其他参数不变的情况下，改变桩间土初始模量Es的大小，由此获得其对桩土应力比的影响如图10所示。根据图10可知：在同一级荷载下，桩土应力比随着桩间土模量的增大而逐渐减小，其减小的幅度呈递减的趋势。在保持桩间土模量不变的情况下，桩土应力比随着荷载的增大而逐渐增大，最后趋于稳定。因此，不同的土质是会影响刚性桩复合地基的承载力的。

图10 桩土应力比随桩间土模量的变化关系

4 结论

刚性桩复合地基由于褥垫层的设置使得复合地基中垫层、桩体及桩间土体组成一个复杂的结构。本文考虑桩土竖向变形的协调作用，引入分级加载的思想，考虑桩间土的非线性特性，提出了刚性桩复合地基桩土应力比计算方法，并经现场试验的验证，证明此方法的合理性与可行性。通过分别计算刚性桩复合地基在不同垫层模量及厚度、桩间土模量、桩长、面积置换率等情况下随荷载变化的桩土应力比，经分析比较得到如下的初步结论：

1)刚性桩复合地基中，桩土应力比随着荷载的增大呈现增大的趋势，但趋势不减小。

2)刚性桩复合地基中桩、桩间土、垫层的性能都会对桩土应力比产生影响，通过调整垫层模量的大小、垫层的厚度可使刚性桩复合地基中的桩、土效应达到最优。

3)桩长的增大会使桩土应力比达某一最大稳定值，说明刚性桩复合地基中存在临界桩长，因此适当增大桩长对提高桩土应力比是有利的。

4)由桩侧摩阻力分布规律图可知：当荷载较大时，摩阻力呈线性分布，而荷载较小时并不具有这一规律，因此基于摩阻力线性分布模式的计算方法不适用于上部荷载较小的情况。

[1] 折学森. 软土地基沉降计算[M]. 北京: 人民交通出版社，1998.

[2] 彭子茂, 刘胜华. 单壁螺纹PVC塑料套管现浇混凝土桩(PTCC桩)地基加固施工工艺研究[J]. 公路工程, 2014, 39(2): 190-196.

[3] 闫明礼, 张东刚. CFG桩复合地基技术及工程实践(第2版)[M].北京: 中国水利水电出版社, 2006.

[4] GB/T 50783-2012，复合地基技术规范[S].

[5] 傅景辉, 宋二祥. 刚性桩复合地基工作特性分析[J].岩土力学，2000,21(4):335-339.

[6] 朱世哲, 徐日庆, 杨晓军，等. 带垫层刚性桩复合地基桩土应力比的计算与分析[J]. 岩土力学, 2004, 25(5): 814-817.

[7] 郭忠贤, 霍达. 刚性桩复合地基桩土应力比计算及承载特性分析[J]. 岩土力学, 2006, 27(5): 797-802.

[8] 赵明华, 陈庆, 张玲. 考虑桩顶剌入变形的刚性桩复合地基桩土应力比计算[J]. 公路交通科技, 2009, 26(10): 38-43.

[9] 缪林昌, 王飞, 吕伟华. 刚性桩复合地基桩土应力比计算方法[J]. 地下空间与工程报, 2014, 10(6): 1270-1274.

[10] 高琼, 赵桂娥. 柔性基础下刚性桩复合地基沉降计算研究[J]. 公路工程, 2013, 38(1): 116-117.

[11] 张军, 郑俊杰, 马强. 路堤荷载下双向增强复合地基受力机理分析[J]. 岩土工程学报, 2010, 32(9): 1392-1398.

[12] 赵明华, 刘猛, 张锐, 等. 路堤荷载下双向增强复合地基荷载分担比及沉降计算[J]. 岩土工程学报, 2014, 36(12): 2161-2168.

[13] 李鹏云, 陈晓国, 张峰. 基于双曲线模型的T型刚性桩荷载传递特性研究[J]. 岩土力学, 2012, 9(S1): 223-228..

[14] 曹文贵, 刘海涛, 张永杰. 散体材料桩桩复合地基沉降计算的分层总和法探讨[J]. 水利学报, 2010, 41(8): 984-990.

[15] 张雁, 刘金波. 桩基手册[M]. 北京: 中国建筑工业出版社, 2009.

[16] 刘杰, 张可能. 复合地基荷载传递规律及变形计算[J]. 中国公路学报, 2004, 17 (1): 20-23.

1008-844X(2017)02-0045-06

U 416.1

A